直升机支柱式前起落架摆振分析

孙为民，方建义

(中国直升机设计研究所，江西 景德镇 333001)

直升机支柱式前起落架摆振分析

孙为民，方建义

(中国直升机设计研究所，江西 景德镇 333001)

根据摆振简化理论推导了一种直升机的支柱式前起落架摆振动力方程。从摆振特性分析中可以看出，在某些状态下，起落架不需要提供阻尼也能保证摆振系统的稳定性。但随滑跑速度的提高，临界当量阻尼有增大的过程。随地面载荷的增加，临界当量阻尼也有增大。在所有状态下，安装在起落架上的减摆器都需要提供足够的阻尼，以保证摆振系统的稳定性。从摆振响应分析中可以看出，响应曲线跟摆振特性分析结果吻合，反证了分析求解过程的合理性。

支柱式起落架；摆振；临界阻尼

0 引言

飞机在起飞和着陆滑跑时，它的前轮可能会出现一种偏离其中立位置的剧烈的侧向摆动。这种摆动的组成主要是前轮摆动部分绕其转向轴周期的摆动，也可能包括前起落架本身和前机身的摆动，严重时，甚至形成从前机身到尾段的整个机身的颤抖。这种复杂的振动就是飞机的前轮摆振[1]。

国外对飞机起落架摆振的分析研究早在20世纪40年代就开始了。国内从60年代初开始研究，并在80年代初建成大型摆振试验专用设备。诸德培等对摆振理论和试验进行了系统的研究，并有相关论著[1-4]。近年有人对柔性飞机的摆振进行研究[5]。但国内在直升机的摆振方面论述较少。

直升机起落架在设计过程中，一般采取增大稳定距和安装摩擦减摆器的方法来防止摆振。在地面试验阶段进行摆振试验，对起落架的摆振稳定性进行检验。不同于液压减摆器，摩擦减摆器的阻尼特性有自己的特点，其阻尼可通过公式推导获得，本文不详述。

本文从摆振简化理论出发，推导直升机支柱式前起落架的摆振动力方程，并进行摆振特性分析和响应分析。

1 起落架摆振动力模型

一种支柱式的双轮前起落架如图1所示，外筒通过安装接头安装在机身结构上，地面载荷通过机轮和缓冲支柱传递给机身。机轮在地面转动的时候，缓冲支柱的旋转筒绕外筒转动。摩擦式减摆器粘接在外筒和旋转筒端面上。根据文献[1]的简化理论构建摆振模型，需要假设：系统是线性的；定向轴是刚固的、垂直的；轮胎在滚动时没有滑移；轮胎的变形特性采用静态刚度特性；轮胎的滚动特性采用点接触理论。

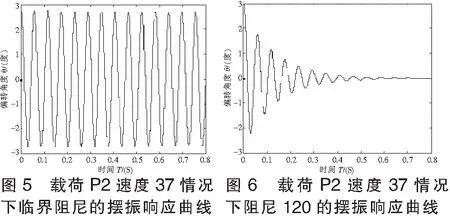
在简化理论中，考虑的运动参数共有三个：机轮摆动角(也叫偏转角)θ、轮胎的扭转变形角φ、轮胎的侧向变形λ。如图2所示，可以建立一个摆动的动力平衡方程， 再加上轮胎的两个滚动约束条件，构成摆振问题的完整方程，如式(1)所示。

这是一个二阶微分方程组，除了三个未知量θ、φ、λ，其余符号分别为：飞机前飞速度V、轮胎的侧向刚度a、轮胎的扭转刚度b、轮胎的纵向刚系数c、前轮距之半τ、轮胎的侧向滚动系数α、轮胎的扭转滚动系数β、对定向轴转动而言的减摆器的阻尼h、整个活动部分(含机轮、旋转筒等)对定向轴的转动惯量I、起落架的稳定距t、机轮向前运动的距离S。

轮胎的刚度系数a、b、c和轮胎的滚动系数α、β可根据经验公式获得[6]，也可根据实测数据获得。转动惯量I、稳定距t和前轮距之半τ等根据设计获得。距离S可以和时间T转换，dS=V*dT。阻尼h可以是根据摆振特性分析得到的临界当量阻尼，也可以是根据临界频率进行减摆器阻尼试验或理论计算得到实际当量阻尼。

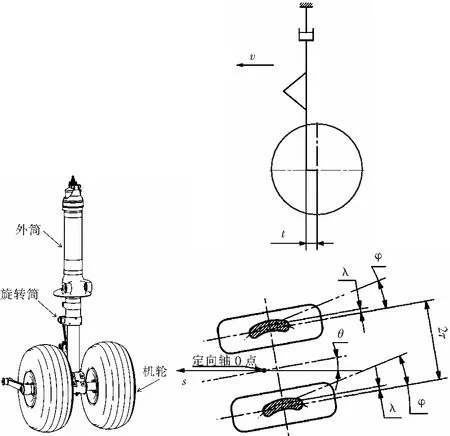
图1 支柱式前起落架 图2 支柱式起落架摆振计算模型

2 摆振特性分析

在起落架摆振问题中，主要关心的是摆振运动的稳定性。“所有起落架应具有固有的，或可增大的能防止振动产生所需的阻尼，以便使起落架振动的振幅在3个周期以后，降到初始振幅的1/3，或者要小于最初的扰动”[7]。这就首先要求对摆振动力方程的稳定性进行分析,求出临界阻尼。根据式(1)可以得到关于特征方程变量X的行列式：

可以化成：

其中：

A0=IV2

A1=hV+βIV2

A2=2cτ2+βhV+2b+2at2+αIV2

A3=2βcτ2+2αbt+2βat2+αhV

A4=2αb+2βat+2αcτ2

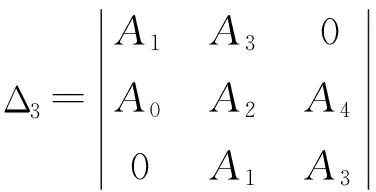
当Δ3>0，则方程式的所有各根只有负值的实部，系统是稳定的。

当Δ3=0，即为系统临界稳定边界。

利用变量置换法解Δ3=0，可以得到：

求解式(4)，即可得到临界当量阻尼h。

摆振圆频率：

摆振频率：

实际算例：

某支柱式前起落架，最大滑跑速度40m/s，根据最大地面载荷将载荷分成7级(用P1-P7表示，P1最小，P7最大)。将轮胎滚动系数等各数据代入式(4)可求得具体滑跑速度和载荷下的临界当量阻尼。图3中给出了七种不同载荷下的摆振临界当量阻尼随滑跑速度的变化曲线，临界阻尼范围为0～141.77N·m·s/rad。临界当量阻尼在某些状态下为0，即起落架不需要提供阻尼都能保证摆振系统的稳定性。但随滑跑速度的提高，临界当量阻尼有增大的过程，某些状态到达最大值后，临界阻尼降低。随地面载荷的增加，临界阻尼也有增大，最大一级载荷的情况下，临界阻尼最大。

根据式(5)、(6)和已经求出的临界当量阻尼h，可求出临界摆振频率。图4中给出了七种不同载荷下的摆振频率随滑跑速度的变化曲线。可以看出，每种载荷下摆振频率随滑跑速度的升高而提高。摆振频率范围在1.98Hz～23.43Hz之间。

固定翼飞机起落架常用的液压减摆器通常要根据摆振频率范围测试出在不同频率时候的实际阻尼，直升机起落架常用的摩擦减摆器也需要根据摆振频率获得其所能提供的实际阻尼,以保证在所有规定的范围内，起落架均能提供足够的阻尼以保证摆振系统的稳定性。

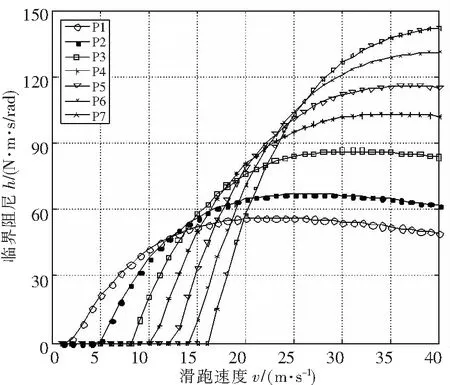
图3 支柱式前起落架摆振临界阻尼曲线

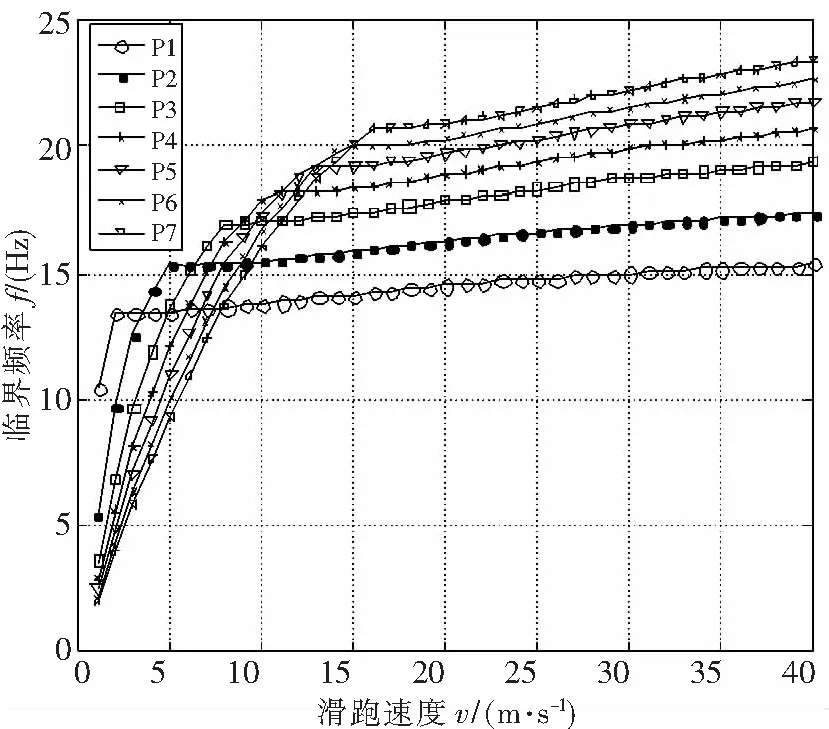
图4 支柱式前起落架临界摆振频率曲线

3 摆振响应分析

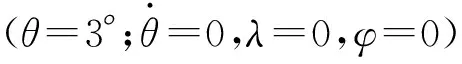
在P2级载荷，滑跑速度37m/s的情况下，临界当量阻尼为64.31N·m·s/rad，频率为17.21Hz。根据这个临界当量阻尼计算摆振响应，计算结果合理的话，响应曲线应当为简谐振动，频率为17.21Hz。响应曲线如图5所示，响应曲线跟摆振特性分析的结果吻合。如果要防止摆振，在这种载荷和滑跑速度情况下，必须保证减摆器能够提供的实际当量阻尼大于64.31 N·m·s/rad。假设实际当量阻尼为120 N·m·s/rad，摆振响应曲线如图6所示。假设实际当量阻尼为40N·m·s/rad，摆振响应曲线如图7所示。从图5-图7可以看出，当实际阻尼小于临界阻尼时，起落架摆振系统收敛、稳定，大于，则发散、不稳定，等于，则为简谐振动。

根据摆振动力方程进行稳定性分析得到的临界当量阻尼，在数值上有可能为负数。而实际情况下，阻尼不为负数，计算中统一将小于或等于0的数值均取值为0。当出现这种情况时，意味着阻尼为0都可保证摆振系统稳定，即不需要提供阻尼，摆振系统都稳定。在P7载荷、滑跑速度6m/s的情况下, 根据摆振特性分析得到临界阻尼为0，频率为12.37Hz，响应曲线如图8所示。可以看出阻尼为0的时候，摆振系统稳定。

通过摆振响应分析，可以看出其结果与前述的摆振特性分析相互吻合。

4 结论

1) 本文从摆振简化理论出发，推导了某直升机支柱式前起落架的摆振动力方程。

2) 对摆振动力方程进行特性分析，计算得到临界当量阻尼范围在0～141.77N·m·s/rad之间。临界当量阻尼在某些状态下为0，即减摆器不需要提供阻尼都能保证摆振系统的稳定性。但随滑跑速度的提高，临界当量阻尼有增大的过程。随着陆载荷的增加，临界当量阻尼也有增大。

3) 对摆振动力方程进行特性分析，计算得到摆振频率范围在1.98Hz～23.43Hz之间。直升机常用的摩擦减摆器需要根据这些频率进行理论计算或减摆器阻尼试验以获得实际当量阻尼，分析实际当量阻尼是否大于临界当量阻尼，以避免摆振发生的可能。

4) 对摆振动力方程进行响应分析，计算得到的响应曲线跟摆振特性分析结果吻合，反证了摆振动力方程的合理性。

[1] 诸德培，等，编著.摆振理论及防摆措施[M]. 北京：国防工业出版社，1984.

[2] 诸德培.飞机主起落架机轮摆振分析[J].航空学报，1992.

[3] 诸德培.飞机前轮摆振及减摆器的若干问题[J].航空学报，1987.

[4] 周进雄,诸德培.起落架结构参数对飞机机轮摆振的影响[M]. 北京：国防工业出版社.1984.

[5] 冯 飞，等.飞机柔性对前起落架摆振的影响分析[M].航空学报.2011.

[6] 航空航天工业部科学技术委员会，编.飞机起落架强度设计指南[M].成都：四川科学技术出版社.1989.

[7] GJB3063A-2008 飞机起落架系统通用规范[S].北京：总装备部军标出版发行部出版.2008.

Shimmy Analysis of a Helicopter Nose Strut Landing Gear

SUN Weimin，FANG Jianyi

(China Helicopter Research and Development Institute，Jingdezhen 333001, China)

A shimmy dynamic equation for a helicopter nose strut landing gear has been deduced according to simplified theory of shimmy. From the shimmy feature analysis, it has been found that dampers don’t be need to assure the stability of shimmy system under some situations. But with the increase of running velocity the critical dampers arise. With the increase of load the critical dampers also arise. The shimmy damper installed on the landing gear needs to supply enough dampers to keep stability of the landing gear system. From the response analysis, it has been found that the response curves agree with the shimmy feature analysis and prove the rationality of the shimmy dynamic equation.

strut landing gear； shimmy； critical damper

2016-03-17

孙为民(1979-)，男，江西都昌人，工学硕士，高级工程师，主要从事直升机着陆装置的设计和性能分析。

1673-1220(2016)04-017-04

V214.1+3；V226+.4

A