倾转旋翼机重心对平衡稳定性的影响分析

孙 敏，孙 强，仲唯贵，朱清华

(1.南京航空航天大学，直升机旋翼动力学国家级重点实验室，江苏 南京 210016；2.中国直升机设计研究所，江西 景德镇 333001)

倾转旋翼机重心对平衡稳定性的影响分析

孙 敏1，孙 强2，仲唯贵2，朱清华1

(1.南京航空航天大学，直升机旋翼动力学国家级重点实验室，江苏 南京 210016；2.中国直升机设计研究所，江西 景德镇 333001)

根据倾转旋翼机的布局特点，建立了包含旋翼、机翼、垂尾、平尾(含舵面)和机身的气动模型及全机飞行力学模型。对不同重心位置模型进行配平分析，在配平的基础上进行了线性模型的提取和分析，给出倾转旋翼机重心包线的计算方法。最后以XV15倾转旋翼机为算例进行不同重心位置的配平、稳定性分析和重心包线计算。结果表明该方法合理有效。

倾转旋翼机；飞行力学特性；配平；重心包线

0 引言

倾转旋翼机具有直升机的垂直/短距起降及悬停功能和飞机的高速平飞能力，这个集直升机和飞机特点于一体的飞行器一直受到人们的青睐，具有很大的发展潜力。20世纪20年代国外就对倾转旋翼机开始了研究，解决了许多关键技术问题，现已有型号列装到部队。国内对倾转旋翼机的研究开始得比较晚，且多数理论都集中在研究旋翼和机翼之间的气动影响，而对倾转旋翼机的重心及其飞行力学特性的研究较少。

飞行器的重心位置直接影响着飞行性能和操纵使用安全，飞行器的重心包线是飞行器在飞行使用中不可逾越的一道安全线，如果装载不当造成重心位置超出重心包线范围，可能会造成机毁人亡的惨剧[1,2]。为了使飞行器的重心始终在安全的重心包线内，其确定显得尤为重要[3，4]。鉴此，本文首先建立了适合倾转旋翼机的飞行力学配平方法，并在此基础上对重心包线进行了计算分析，形成了重心包线设计方法，并在此基础上开展了重心对飞行器平衡性和稳定性的影响规律研究。

1 气动力建模

1.1 右(左)旋翼气动力模型

直升机模式和倾转模式下旋翼既有总距操纵也有周期操纵，提供飞行时的升力和推力，同时也是飞行姿态的控制面。飞机模式下旋翼只有总距操纵，没有周期操纵，仅仅提供前飞的推力。

旋翼气动力计算的关键是其周围诱导速度的计算，诱导速度影响翼型的迎角和气动力，不同的气动力会引起桨叶不同的挥舞运动，不同的挥舞运动将改变桨叶的周围环境，反过来又影响翼型的诱导速度和气动力，是一个相互影响的循环过程，它们的相互关系如图1所示。

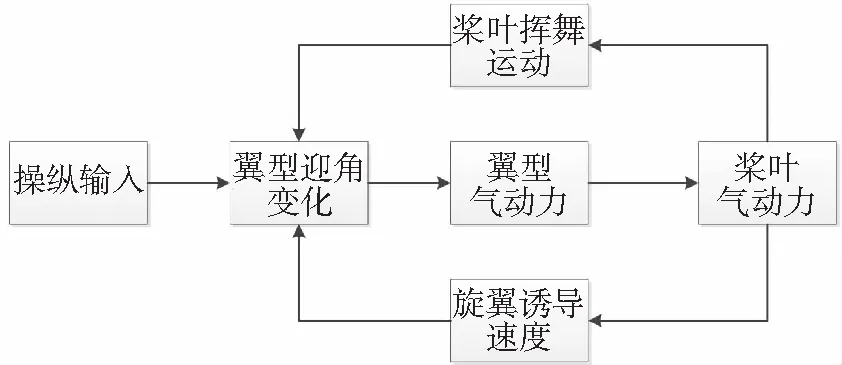
图1 旋翼气动特性及其相互影响

旋翼气动力计算中的诱导速度由已经发展很成熟的动态入流模型求得，桨叶气动力采用叶素理论计算，桨叶挥舞角由桨叶挥舞运动方程计算。具体求解步骤(以右旋翼为例)如下：

1)给定初始的机体前飞速度、诱导速度基频值、诱导速度纵横向分布值、桨叶预锥角和纵横向挥舞角；

2)由机体坐标系下的速度计算旋翼构造轴系下桨毂处的速度，由桨毂处的速度计算不同叶素处的速度，并转换到翼型构造轴系中；

3)根据诱导速度和2)的翼型构造轴系中的气流速度算出翼型的迎角，进而由翼型气动数据算出此处叶素在翼型构造轴系中的气动力分量(垂向力、径向力和切向力)；

4)将气动力带入桨叶挥舞运动方程可以求得桨叶的挥舞角，由动态入流模型算得诱导速度；

5)根据桨叶的挥舞角可以算出叶素在旋翼构造轴系下的旋翼拉力(TR)、后向力(HR)、侧向力(SR)、扭矩(QR)、俯仰力矩(MR)、和滚转力矩(LR)，并转换到机体坐标系下。

本文左右旋翼的旋翼构造轴系方向为一致，只是原点位置不同，这样可以利用同样的坐标转换矩阵将左右旋翼的气动力转换到机体坐标系中。由于右旋翼为逆时针方向(俯视)旋转，而左旋翼为顺时针旋转，所以由对称原理可以得到左旋翼的气动力：

[TL，HL，SL，QL，ML，LL]=

1.2 右(左)机翼和副翼气动力模型

在小速度直升机模式下左右机翼没有副翼的操纵输入，飞机模式下左右机翼有副翼的操纵输入。为了考虑旋翼尾流对机翼气动力的影响，将机翼分为自由区和滑流区，自由区为不受旋翼尾流影响的区域，滑流区为受旋翼尾流影响的区域[5]。

滑流区在超过一定速度时不考虑旋翼尾流的影响，即此时的滑流区面积为零，当低于一定前飞速度时考虑旋翼尾流的影响。滑流区面积的计算是比较复杂的，本文采用以下的经验公式计算滑流区的面积(以右机翼为例)：

其中，R为旋翼对机翼的影响半径，βs为影响系数，b为机翼平均弦长，in为旋翼的倾转角，umax为旋翼尾流偏出机翼时的旋翼前进比。自由区的面积为机翼总面积减去滑流区面积。

滑流区机翼的速度为：

其中，[vx,vy,vz][wx,wy,wz]为机体线速度和角速度，η为诱导速度影响系数，1≤η≤2，vi为旋翼平均诱导速度。

滑流区升阻力等参数如下：

Lwass_r=qwass_rSwass_rCLwass_r

Dwass_r=qwass_rSwass_rCDwass_r

(∂CLwass_r/∂δail)δail

αwass_r=arctan(vy_wss_r/vx_wss_r)

对于自由区气动力的计算只需将η设定为0，即消除旋翼尾流对机翼的诱导速度影响，其他计算过程保持一致。同时，由于对称原理，左机翼气动力的计算和右机翼的分析过程一样。

1.3 机身气动力模型

机身气动力的计算比较复杂，一般倾转旋翼飞行器不考虑机翼和旋翼对机身气动力的影响。由风洞试验可以测得气动力系数[Cx_f,Cy_f,Cz_f]和力矩系数[Mx_f,My_f,Mz_f]，它们随机身迎角和侧滑角改变而改变；机身的特征面积和特征长度分别为Af和Lf；设机身的气动压力中心为[xf,yf,zf]，则机身的气动力和力矩计算如下:

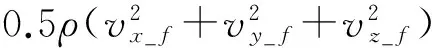
1.4 尾翼气动力模型

由于机身、机翼和旋翼等部件都对平尾产生气动干扰，真实地计算这些气动干扰复杂而困难[7]。本文用动压损失系数khs代替机身、机翼和旋翼等部件对平尾的气动干扰作用，设平尾的气动压力中心为[xhs,yhs,zhs]，则平尾的气动压力中心来流速度为：

由平尾和升降舵产生的气动力系数如下：

CD_hs=cd+CL_hsCL_hs/(λπ)

由平尾和升降舵在机体质心处产生的气动力和力矩为：

其中，lc为平尾弦长与升降舵弦长之比，λ为平尾展弦比，ζ升降舵型阻系数，TB为平尾风轴系到机体坐标系的转换矩阵。

垂尾和方向舵的气动力建模与平尾和升降舵相似，注意将TB替换成垂尾风轴系到机体坐标系的转换矩阵即可。

2 全量方程

2.1 机体欧拉方程及其补充方程

运动方程采用机体坐标系，原点定在机体的质心处，X轴为机体构造基准线向前，Y为垂直X轴向上，和X轴构成机体的纵向对称面，Z轴垂直纵向对称面向右。

6自由度欧拉方程：

ϑ+Fx/m

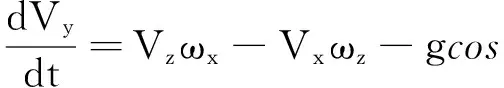
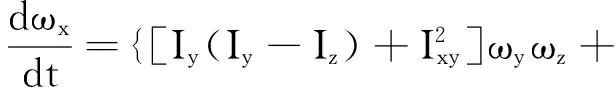
机体姿态角与角速度之间运动学关系的补充方程：

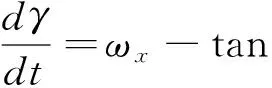
2.2 旋翼挥舞运动方程组

右(左)旋翼挥舞运动方程(假设挥舞角为一阶谐波量)：

其中：

b1=-eMsΩ2/Ib

b2=2Ω

b3=-γΩ2/(σα)

b4=γΩ/8

2.3 旋翼诱导入流方程组

右(左)旋翼诱导速度方程：

其中，V0、Vs和Vc分别为诱导速度基频值、纵横向分布值，[A]、[B]为动态入流模型的系数矩阵。

方程组(9)、(10)、(11)、(13)共同组成倾转旋翼机的飞行力学模型，这23个非线性微分方程可用一般的函数描述为：

其中，X是系统状态变量，U是系统控制变量，最终对上述非线性微分方程组(14)进行求解配平。

3 飞行力学模型验证

为了表明本文飞行力学模型的合理性，用文献[8]中的算例进行验算，结果如图2所示。可以看出直升机模式(0～140km/h)总距和纵向周期变距及飞机模式(280～450km/h)纵向周期变距配平结果与文献结果相吻合。飞机模式总距配平结果略有不同，这可能是算例机身阻力系数不同引起的。对比结果表明本文建立的飞行力学模型合理可行。

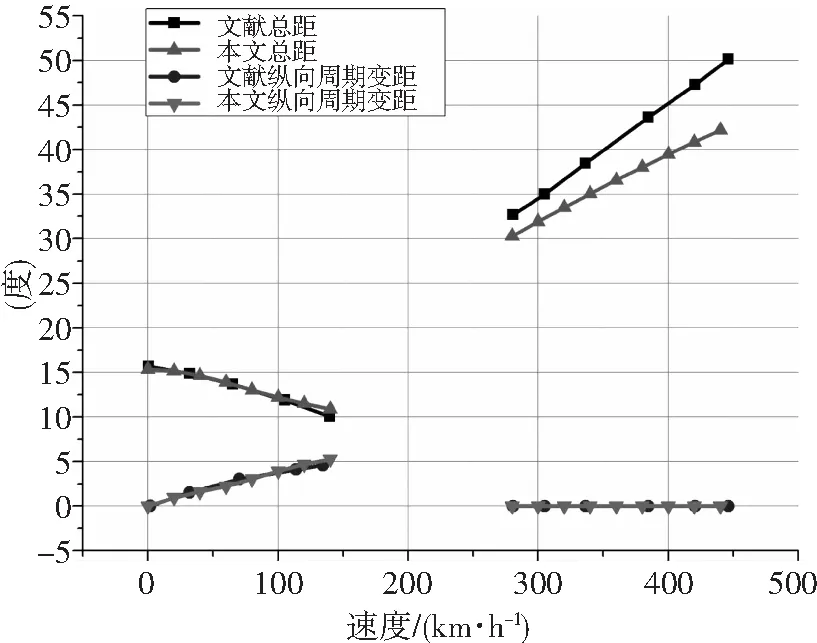
图2 直升机模式和飞机模式下总距/纵向周期

4 倾转旋翼机重心包线计算方法

根据倾转旋翼机重心位置对操纵性和稳定性的影响，在上文建立的飞行力学模型基础上进行了重心范围的计算。在使用中垂向的高低重心变化范围一般较小，同时三维重心包线迭代计算需要耗费大量时间，故本文仅计算了二维前后左右重心包线(本文方法也可计算垂向重心范围)。主要计算步骤如下：

1)输入倾转旋翼机原始参数、操纵范围限制量及初始重心位置；

2)固定重心坐标z值，在不同的前飞速度下计算旋翼、机翼等部件的气动力，带入飞行力学模型，并完成配平；

3)对配平结果进行线性化处理，并完成稳定性分析，判断系统特征根是否出现正实数，如果出现则输出重心位置的前限值和后限值并执行第5步，如果没有则执行第4步；

4)根据配平结果输出每个速度下的操纵量，判断操纵量是否超出飞行器操纵范围限制量，如果超出则输出重心位置的前限值和后限值，如果没有超出则将重心坐标沿x轴向前(或向后)增加一个步长值并返回第2步，具体流程如图3所示；

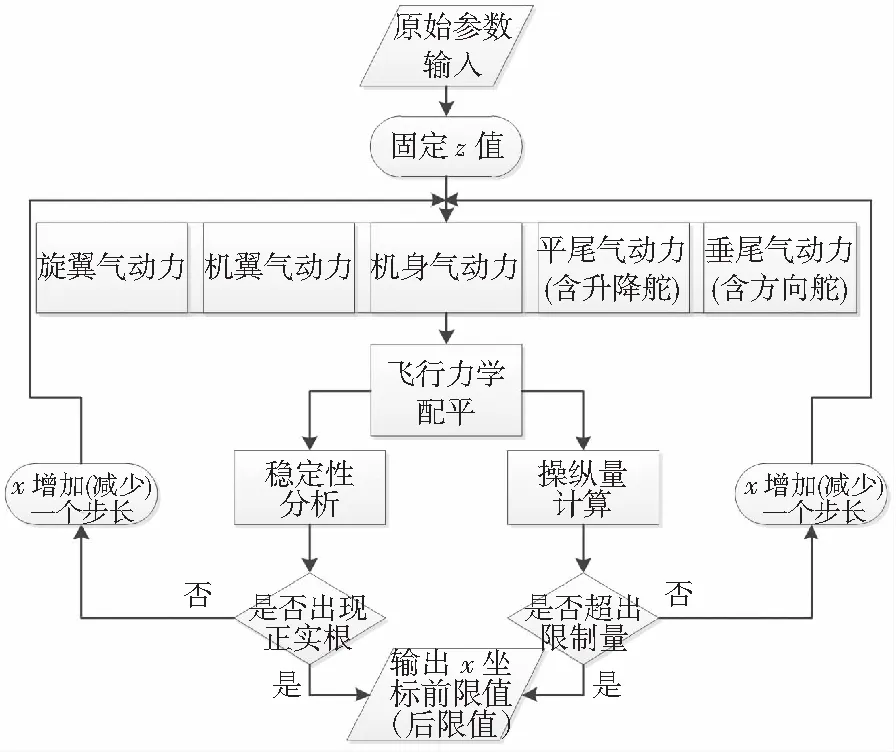
图3 重心包线前后限计算流程图

5)在得到的重心前限值和后限值范围内均匀分成若干段，对于每个x值，固定其坐标，变化z坐标寻找此x坐标对应的左限值和右限值(迭代步骤如同寻找前后限值)；

6)最后将计算得到的重心前后限值和左右限值拟合成二维曲线，即为倾转旋翼机的重心包线图。

以上确定的是对应某起飞重量时的飞行器重心包线，如果计算出对应飞行器全部可能的使用重量时的重心包线，就等于确定了使用重心包线。

5 算例分析

为说明本文飞行力学建模的有效性，首先以XV15倾转旋翼飞机为例对不同重心位置的直升机模式(0～140km/h)和飞机模式(280～480km/h)进行了配平计算，得到各个气动部件的操纵量；然后在配平的基础上运用线性理论得到线性模型，分析这23个特征向量，从中找出对应机体运动方程的9个特征根；最后，运用该飞行力学模型根据稳定性和操纵量限制对XV15倾转旋翼机进行重心包线的计算。

5.1 重心位置变化对操纵量的影响

直升机模式下的配平操纵输入量为左右旋翼总距、纵横向周期变距、平尾升降舵偏角(下偏为正)；飞机模式下的配平操纵输入量为左右旋翼总距、副翼偏角(下偏为正)和平尾升降舵偏角(下偏为正)。图4为直升机模式下(0～140km/h)原始重心位置和重心右移1m左右旋翼总距操纵量随前飞速度的变化。图5为飞机模式下(280～480km/h)的原始重心位置和重心右移1m左右副翼的偏角随前飞速度的变化。

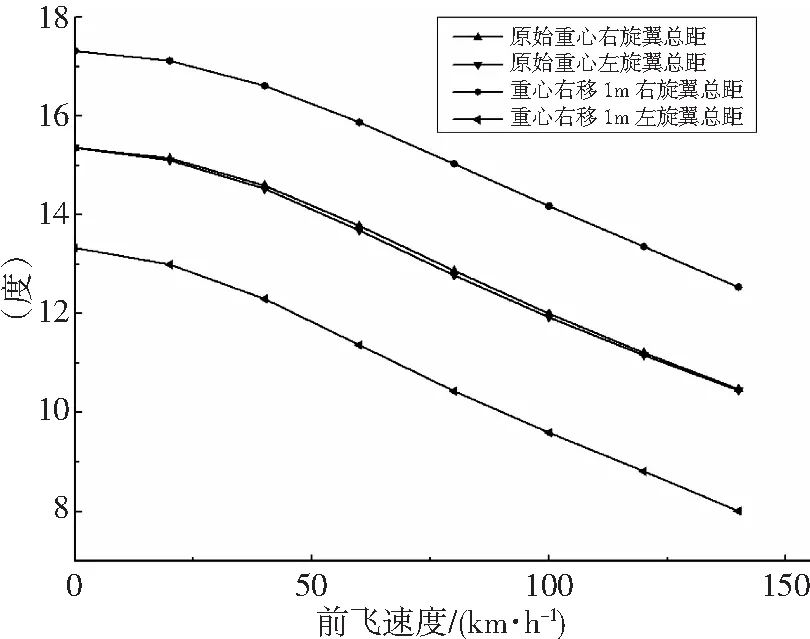
图4 直升机模式左右旋翼总距变化

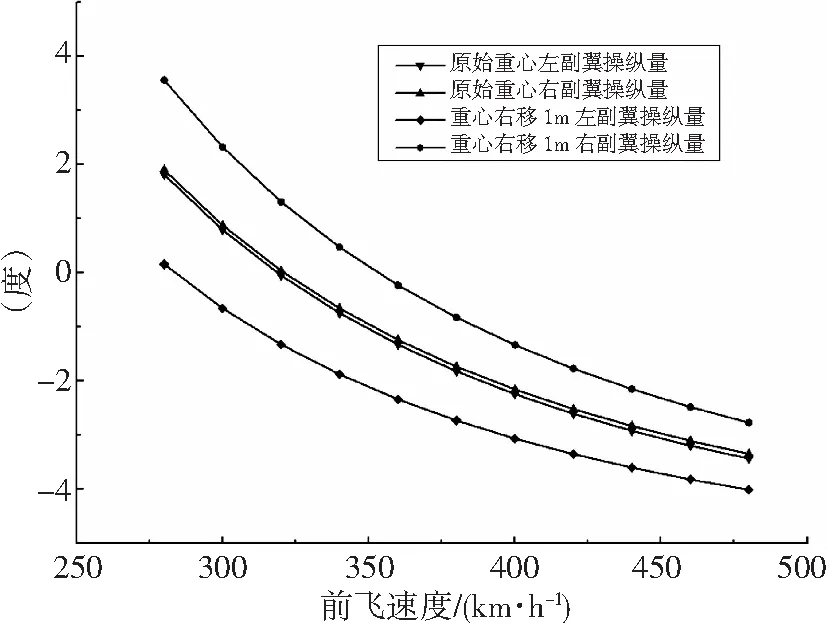
图5 飞机模式副翼偏角变化

从图4可以看出，直升机模式下，在原始重心位置，倾转旋翼机做稳定对称飞行时，左右旋翼的总距操纵量几乎一样，说明左右旋翼产生的升力对等，也说明所建立的飞行力学模型的合理性。同时可以发现总距操纵量随前飞速度的增加而逐渐减小，这是由于随着前飞速度的增加，机翼产生升力，给左右旋翼卸载，所需的总距操纵量自然会减小。对比原始重心位置和重心右移1m时的总距操纵量，可以发现当重心向右移动时，右旋翼总距有所增加而左旋翼总距有所减少，左右旋翼产生升力差以克服由于重心右移产生的滚转力矩。

从图5中可以发现，飞机模式下，在原始重心位置，倾转旋翼机稳定对称飞行时，左右机翼产生的升力几乎一样，当重心向右移动时主要靠左右机翼产生升力的差值来平衡。随着前飞速度的增加，副翼的偏角减小，这是因为速度增加，机翼可以产生更大的升力，需要副翼产生的升力会减小。仔细观察重心右移1m时左右副翼的操纵量差值，可以发现其随前飞速度增加而减小，这是由于副翼偏角相同时，前飞速度越大，产生的升力越大，所以产生同样的升力差时，前飞速度越大，副翼的偏角越小。

5.2 重心位置变化对稳定性的影响

根据配平结果进行线性模型的分析，提取9个特征根(其中一个零特征根对应航向运动)。图6为直升机模式下倾转旋翼飞机特征根分布图，其速度范围以20km/h间隔从0km/h到140km/h，配平得到线性模型，再求得模型的特征根。图7为飞机模式下的倾转旋翼飞机特征根分布图，其速度范围以20km/h间隔从280km/h到480km/h，配平得到线性模型，再求得模型的特征根。箭头所指方向为速度增加的方向。

图6 直升机模式特征根分布图

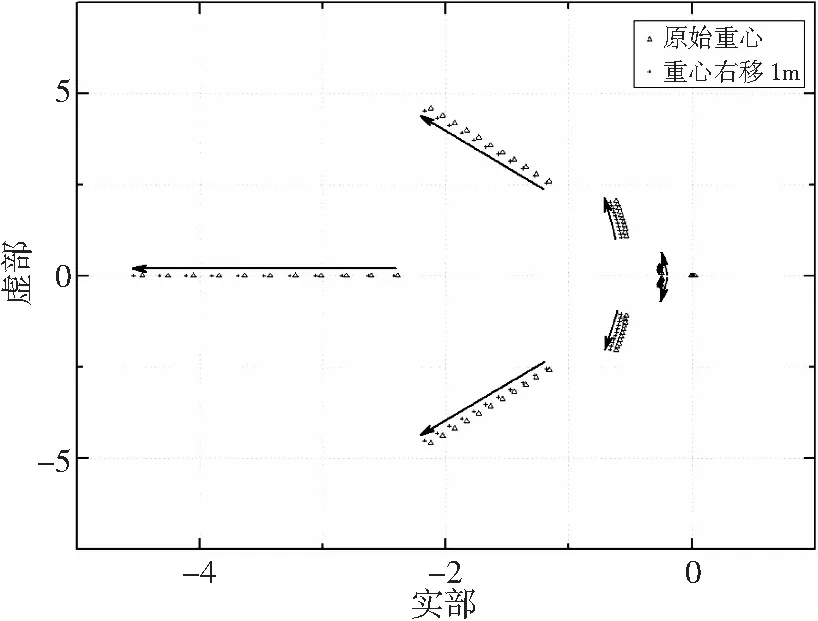
图7 飞机模式特征根分布图

从图6和图7中可以看出，随着速度的增加，9个特征根都向左半平面移动，说明速度增加稳定性越好。对比原始重心位置和重心右移1m的特征根分布，可以发现重心右移对特征根的分布影响不大。

5.3 重心包线的计算

根据前面建立的飞行力学模型和重心包线的计算方法，以XV15倾转旋翼机正常起飞(总重5902kg)为算例分别计算了直升机模式和飞机模式的重心包线。根据两种模式的计算结果拟合得到最终的重心包线。

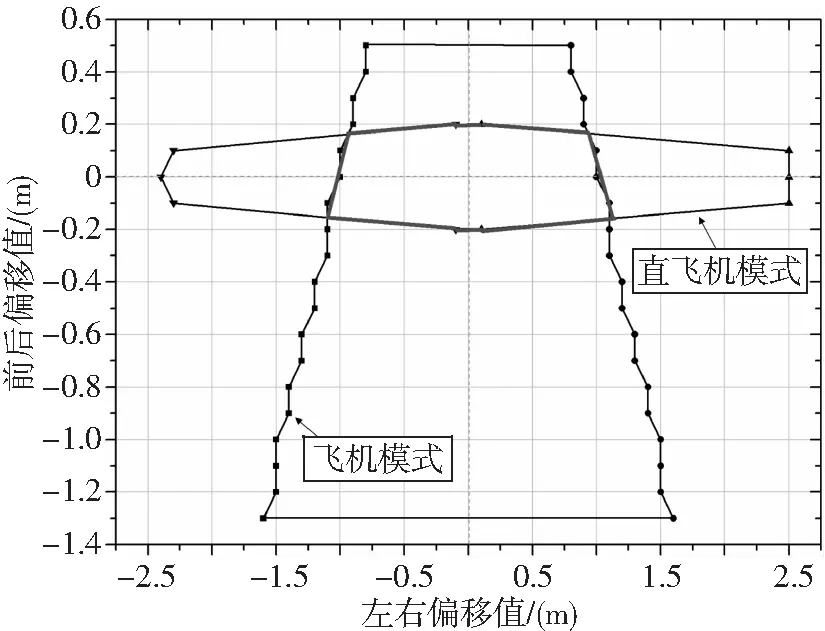
图8 倾转旋翼机重心包线图

图8中飞机模式和直升机模式包线的相交区域为倾转旋翼机的最终重心包线。从图中可以看出，直升机模式的重心前后限小于飞机模式，这是因为飞机模式的飞行速度高于直升机模式，平尾纵向配平能力远高于直升机模式。直升机模式的重心左右限大于飞机模式，这是因为当重心左右移动时，直升机模式下左右旋翼通过总距差平衡滚转力矩，而飞机模式下副翼平衡滚转力矩的能力较小。可以得出结论，直升机模式决定重心包线前后限,飞机模式决定重心包线左右限。

飞机模式重心的前限值小于后限值，这是由于本算例的机翼的气动中心位于原始重心之前，在重心没有偏移时就已产生抬头力矩，当重心向前偏移时会产生更大的低头力矩，而升降舵偏角是有限的。

6 结论

1) 本文建立了倾转旋翼机左右旋翼、左右机翼、机身、升降舵、平尾和垂尾的非线性气动模型和飞行力学模型，算例验证了其正确有效。该模型适用于倾转旋翼机配平计算和气动部件布局分析。

2) 本文重心包线计算方法为倾转旋翼机总体设计阶段重量分布及装载方案提供一种合理依据。

3) 直升机模式重心位置左右移动主要靠左右旋翼总距差动实现平衡飞行；飞机模式重心位置左右移动主要靠左右副翼不对称偏动实现平衡飞行。

4) 直升机模式下，旋翼总距操纵量随着前飞速度增加而减小；飞机模式下，副翼偏角随前飞速度增加而减小。

5) 倾转旋翼机重心包线前后限主要受直升机模式的限制,左右限主要受飞机模式的限制。建议研制倾转旋翼机时可以通过直升机模式确定重心包线前后限，通过飞机模式确定重心包线左右限。

[1] 王小平.民用飞机重心包线研究[J].民用飞机设计与研究,2011(02):8-10+55.

[2] 张 晶,申功璋,杨凌宇.飞机主动重心控制系统设计及应用[J].飞行力学,2008(06):68-72.

[3] 税清才,王秋萍.飞机重心允许范围设计准则[J].飞行力学,2003(02):63-66.

[4] 葛 磊.面向倾转旋翼机总体方案阶段的重心包线设计研究[D].南京：南京航空航天大学,2012.

[5] 曹芸芸.倾转旋翼飞行器飞行动力学数学建模方法研究[D].南京：南京航空航天大学,2012.

[6] 程 尚.倾转旋翼飞行器建模及仿真研究[D].南京：南京航空航天大学,2010.

[7] 徐 恺.倾转旋翼飞行器旋翼/机翼/机身气动干扰计算[D].南京：南京航空航天大学,2007.

[8] 曹芸芸.倾转旋翼飞行器操纵策略和配平方法[J].南京航空航天大学学报,2009.

Analysis of the Influence of the Gravity Center of Tilt Rotor Aircraft on the Trim and Stability

SUN Min1，SUN Qiang2，ZHONG Weigui2，ZHU Qinghua1

(1.National Laboratory of Science and Technology on Rotorcraft Aeromechanics,Nanjing University of Aeronautics & Astronautics, Nanjing 210016, China；2.China Helicopter Research and Development Institute，Jingdezhen 333001, China)

According to the features of the layout of tilt rotor aircraft, this paper established flight dynamics model includes rotor, wing, fin and tail plane (including elevator) and fuselage dynamic model. Trim analysis was carried out on the model, extraction and analysis of linear model was carried out on the trim, the center of gravity envelop calculation method of the tilt rotor aircraft was given. Finally, the trim, stability analysis and center of gravity envelope calculation was carried out with the example of the xv15 tilting rotary rotor aircraft. The results show that the method is reasonable and effective.

tilt rotor aircraft; flight dynamic characteristics; trim; center of gravity envelope

2016-08-09

孙 敏(1992-)，男，安徽马鞍山人，硕士研究生，主要研究方向：直升机总体气动。

1673-1220(2016)04-006-06

V212.4 ；V221+.5

A