y= k/x（k≠0）中k值几何意义的应用

□

y= k/x（k≠0）中k值几何意义的应用

□邹新

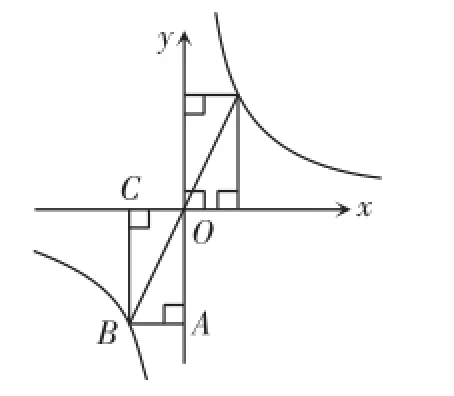
图1

一、与等积变形相结合运用k值的几何意义

例1如图2，已知点A在反比例函数y＝k＞0）上，作Rt△ABC，

点D为斜边AC的中点，连DB并延长交y轴于点E，若△BCE的面积为8，则k＝.

解析：连接AE、AO.

如图2，∵点D为AC的中点，

图2

∴S△DEC＝S△DEA，S△DBC＝S△DBA，

∴S△BEC＝S△BEA＝8.

又∠ABC＝90O，∴AB∥y轴，

由等底等高的三角形面积相等

可得S△BEA＝S△BOA＝8＝|k|，

∴k＝±16.

又k＞0，∴k＝16.

点评：灵活等积变换后结合k值的几何意义解题是关键.运用“等底等高的三角形面积相等”进行等积变形是比较常用的方法.

例2双曲线y1＝在第一象限的图象如图3所示，过y2上的任意一点A，作x轴的平行线交y1于B、交y轴于C，过A作x轴的垂线交y1于D、交x轴于E，连接BD、CE，则

图3

解析：连接BE、CD、OB、OD，

如图3，由AC∥x轴可得，

S△EBC＝S△OBC＝

又AD⊥x轴，则AD∥y轴，

分别过点D、B作△CDE、△EBC的高DM、BN.运用三角形面积公式可证明BN＝DM.

易证四边形NMDB为矩形，

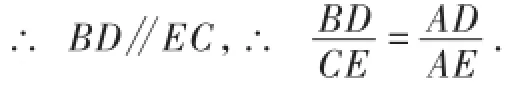
点评：利用k值的几何意义实施等积变形是解题的关键.

例3如图4，一次函数y＝ax＋b的图象分别与x轴、y轴交于点M、N，与反比例函数y＝的图

象相交于点A、B.过点A分别作AC⊥x轴，AE⊥y轴，垂足分别为C、E.过点B分别作BF⊥x轴，BD⊥y轴，垂足分别为F、D.AC与BD交于点K.若点A、B分别在反比例函数y＝的图象的不同分支上.则：

①S四边形AEDK与S四边形BFCK相等吗？

②AN＝BM吗？

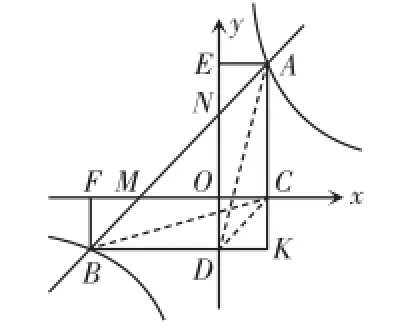
图4

解析：①

如图4，易证四边形BFCK、AEDK、CODK、AEOC、BDOF

均为矩形.

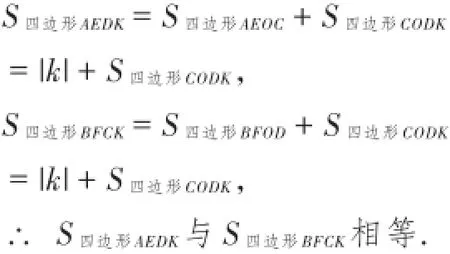
②如图4，连接DC、DA、BC，

设B的坐标为（x，y），

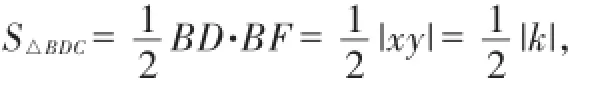
仿例2可证CD∥AB.

易证四边形ANDC、MBDC为平行四边形，

∴AN＝DC＝BM.

即AN＝BM.

点评：本题通过应用k值的几何意义，简化了等积变形的过程，与例2比较，解题过程更简洁.

二、与相似三角形结合运用k值的几何意义

例4如图5，在x轴的上方，直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别与函数y＝的图象交于B、A两点，则∠OAB大小的变化趋势为（）.

A.逐渐变小B.逐渐变大

C.时大时小D.保持不变

解析：分别过点B、A作x轴的垂线，设垂足为C、D，

图5

则由k值的几何意义可得，

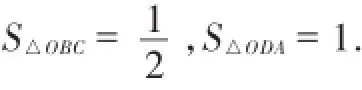
易证△OBC∽△OAD，

在Rt△OBA中，

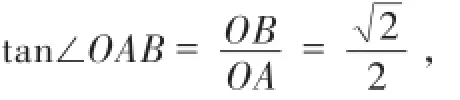
所以锐角∠OAB大小保持不变.故选择D.

点评：本例利用反比例函数中k值的几何意义，结合相似三角形、解直角三角形的知识解题，思维具有跳跃性，有利于培养解题的转化意识.

“学而时习之，不亦说乎？”我们平时在学习的过程中能自觉总结，自然能取得举一反三的效果.探究解题方法的数学解题是非常有乐趣的事情.