基-4高维离散傅立叶变换PM向量编码算法

徐 妍,杨齐琪,余 玲

(北京服装学院 材料科学与工程学院，北京 100029)



基-4高维离散傅立叶变换PM向量编码算法

徐 妍,杨齐琪,余 玲

(北京服装学院 材料科学与工程学院，北京 100029)

离散傅立叶变换是数字信号处理中一种很重要的数学工具，它可以描述离散信号的时域与频域的关系，在数字信号处理中有着重要的地位，应用十分广泛[文献1-3]。本文提出的基-4PM向量编码算法是结合PM算法[文献4]和向量编码算法[文献5-6]创造出的新算法。在采样点数相同的情况下，与现行的几种算法相比，该算法在计算量和运算时间上都有不同程度的降低，从而提高了运算效率。这在实际应用中具有重要的意义。

离散傅立叶变换;行列算法;PM算法;向量编码算法;PM向量编码算法

1 引言

高维离散Fourier变换 (DFT) 的一般形式为

(1)

对高维DFT的计算通常采用行列算法，即将m维DFT化为m个一维DFT计算：

X(a1，a2,…,am)

(2)

对每个一维DFT采用Cooley-Tukey的快速算法计算。行列算法是目前最为常用的计算高维DFT的算法，它的计算效率取决于一维DFT的计算效率。这种算法虽然程序结构较其他算法简单，但就高维DFT变换的特点来说，算法的运算量还是可以进一步减少的。

本文讨论的基-4 PM向量编码算法，是将高维PM离散傅立叶变换的快速算法(Plus-Minus Fast Discrete Fourier Transform Algorithm)与向量编码算法相结合，得到一种新的FFT算法，在采样点数相同的情况下，能够减少执行高维DFT的位码倒序、同址运算和蝶形运算所消耗的时间，与现行的行列算法相比，计算的结构复杂度大大降低，减少了计算量，从而有效的提高了算法的运算效率。

2 高维PM向量编码算法

为了使问题简化，假定各维的采样点数相同，即N1=N2=…=Nm=N，则(1)式可表示为：

X(a1，a2,…,am)

(3)

X(a1，a2,…,am)

(4)

∴(4)式可写作：

X(a1,a2,…,am)

(5)

在(5)式中，将：

设a(b1,b2,…,bm)

(6)

对每一个整数序列(b1,b2,…,m)，该和式可看作是一个m维的u×u×…×u点DFT。在(6)式中，随着ik(1,2,…,m)是不同取值，可得到不同的输入序列，将全部输出结果，记为向量形式：

a(b1,b2,…,bm)

={aq1q2…qm(b1,b2,…,bm):qk=0,1,…,u-1,

k=1,2,…,m}

(7)

可以看出

所以有：

aq1q2…qk…qm(b1,b2,…,bm)

=aq1q2…qk+u…qm(b1,b2,…,bm)

其中：

qk=akmodu

(qk=0,1,…,u-1,k=1,2,…,m)。

因此，将新的输入向量代入到(5)式中，就有：

X(a1,a2,…,am)

会来的。一定会来的。信里讲了会来，就一定会来。何牦深信无疑。他随身带了一张凳子，每天坐在街口等欧阳橘红，怕她找不到竹溪街47号。

(8)

设q=q1,q2,…,qm，则(8)式可改写为：

X(a1,a2,…,am)

(9)

(10)

∴ (10)式可写作：

(11)

对应输入向量aq(b1,b2,…,bm)，记输出向量为Ap(b1,b2,…,bm)，则输出向量为：

A(a1,a2,…,am)

={Aj1j2…jm(a1,a2,…,am)；jk=0,1,…,u-1,k=1,2,…,m}

(12)

则(11)式可被等价的表示为：

Ap(a1,a2,…,am)

(13)

(14)

类似地，可给出IDFT的定义式，这里就不再进行详细的讨论了。

3 基-4算法

γ(0)=(0,0,…,0,0)γ(1)=(0,0,…,0,1)

γ(2)=(0,0,…,0,2)γ(3)=(0,0,…,0,3)

γ(4)=(0,0,…,1,0)…

γ(4m-1)=(3,3,…,3,3)

例如：当m=2时，

(0,0),(0,1),(0,2),(0,3),

(1,0),(1,1),(1,2),(1,3),

(2,0),(2,1),(2,2),(2,3),

(3,0),(3,1),(3,2),(3,3),

共有4×4=16个基-4向量。

τ=40τ0+41τ1+42τ2+…+4n-1τn-1

(15)

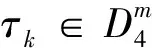
例如：

17=40×1+41×0+42×1

42=40×2+41×2+42×2

则其展开式为：τ=(17,42)=40(1,2)+41(0,2)+42(1,2)

又如：

2=40×2+41×0+42×0

7=40×3+41×1+42×0

50=40×2+41×0+42×3

则其展开式为：τ=(2,7,50)=40(2,3,2)+41(0,1,0)+42(0,0,3)

称(15)式为按基-4向量的编码。

(16)

由(16)式，可将(14)式中的Ap(α)记为：

Ap(α)=Ap(α0,α1,…,αw-1)，

aq(β)=αp(β0,β1,…,βw-1)

(17)

将(16)式代入到(14)式中，由向量点积和数量乘法，则有：

(18)

对∀k=0,1,…,w-1，∵u=2t且u的取值为能整除N的较小的整数， ∴w-1>t

(19)

∵4w+t=N

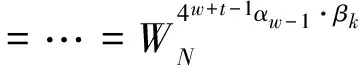
(20)

(21)

(22)

对∀k=0,1,…,w-1

(23)

∵4t=u

(24)

因此，

(25)

由(21)、(25)式有：

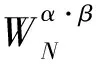
(26)

将(26)式代入到(14)式中，则得到基-4高维DFT的PM向量编码快速算法：

Ap(α)=Aq(α1,α1,…,αw-1)

(27)

当u=4即t=1时，(27)式可写成：

Ap(α)=Ap(α1,α1,…,αw-1)

(28)

其中αq(β0,β1,…,βw-1)的计算由(6)式得到。即：

αq(β0,β1,…,βw-1)=αq(b0,b1,…,bm)

(29)

(28)式即为u=4(t=1)时的高维基-4PM向量编码算法，(29)式为PM向量编码算法的输入向量，此输入算法可由向量编码算法得到。

[1]蒋增荣，曾泳泓，余品能 . 快速算法[M]. 北京：国防科技大学出版社，1998.

[2]DuraisamySundararajan，M.OmairAhmad，M.N.S.Swamy.VectorComputationoftheDiscreteFourierTransform，IEEETransactionsonCircuitsandSystems-Ⅱ:AnalogandDigitalSignalProcessing，1998，45(4)：449～461.

[3]陈兆斗，张志刚 . 高维离散Fourier变换的一种快速算法[J]. 自然科学进展，1999，9(9)：780～782.

[责任编辑：张怀涛]

2015-12-06

北京市科研训练项目(编号：BKSP02150202/009)

徐妍,女，主要从事应用数学方面的研究。

O

A

1671-5330(2016)05-0066-05