基于改进差分进化算法的多阈值图像分割①

杨兆龙, 刘秉瀚

(福州大学 数学与计算机科学学院, 福州 350108)

基于改进差分进化算法的多阈值图像分割①

杨兆龙, 刘秉瀚

(福州大学 数学与计算机科学学院, 福州 350108)

阈值法是一种简单有效的图像分割技术. 但是阈值法也有着明显的缺点, 即阈值求解的计算量随阈值的增加而指数级增长. 为克服多阈值图像分割计算量大、运算时间长的缺点, 引入改进的差分进化算法, 提出新的变异策略, 采用自适应的缩放因子和交叉系数,并新增扰动策略. 改进的算法将多阈值分割模型视为优化问题,将最大类间方差法作为目标函数, 实现多阈值分割. 实验结果表明, 和其它算法相比, 该算法不仅可以取得正确的分割结果, 而且分割速度更快.

图像分割; 多阈值; 差分进化算法; 最大类间方差; 灰度图像

图像分割目的是将一幅图像划分成若干个具有某种均匀一致性的区域, 把人们“感兴趣的目标物”从复杂的场景中提取出来. 阈值分割法是一种传统的图像分割方法, 因其实现简单、性能较稳定而成为图像分割中最基本和应用最广泛的分割方法. 其中阈值的选取是图像阈值分割方法的关键技术. 常见的计算阈值的方法有最大类间方差法(Otsu算法)[1]、最大熵法[2,3]和最小误差法[4]等. 上述计算阈值方法基本是在满足一定准则下通过解析式求得阈值. 比如Otsu算法利用图像灰度的一维概率直方图, 以最大可分性为准则,自适应地选取分割阈值, 实现图像分割, 具有算法简单易实现的优点. 但是包括Otsu算法在内的通过解析式求解阈值的算法, 当扩展到多阈值图像分割时, 搜索空间大、计算复杂度高、计算量大和耗时长的缺点便呈现出来.

图像多阈值分割可以被视为一个优化问题, 因此很多学者将智能优化算法应用于阈值求解. 比如: 基于遗传算法[5]、基于改进量子粒子群优化算法[6]、基于萤火虫算法[7]、基于反向萤火虫算法[8]、基于改进鱼群算法[9]和回溯搜索优化算法[10]等等. 这些基于智能优化的分割算法的优化函数常采用Otsu方法或熵函数,设计一些独特的计算技巧来提高算法的性能, 运用智能优化达到求解所要分割图像的优化函数的目的.

差分进化算法(Differential Evolution DE)[11]是1997年由Storn和Price提出的一种基于种群迭代的随机搜索算法, 该算法从原始种群开始, 先通过交叉、变异、选择几种遗传操作来衍生出新的种群, 然后通过逐步迭代, 不断进化实现全局最优解的搜索, 因此也是一种并行随机搜索算法. 差分进化算法具有原理简单、控制参数少、鲁棒性强、收敛速度快等优点. 因而引起了众多学者的关注, 提出了很多基于差分进化算法的改进及应用[12-17]. 其中文献[17]将改进的差分进化算法应用与图像的多阈值分割中, 实验取得了较好的结果.

文献[17]提出基于Beta分布的缩放因子和交叉系数, 两个参数在区间[0,1]范围内有更高的频率取到两端极值. 这样算法在大部分迭代过程中两个参数可以在区间[0,1]上取到不同的极值, 产生全新的个体, 加强算法搜索过程, 改进原算法中缩放因子和交叉系数保持不变的缺陷. 然而差分进化算法的搜索性能取决于全局探索和局部开发能力的平衡, 而这在很大程度上依赖于算法的控制参数选取, 包括变异策略、缩放因子和交叉概率等[18]. 文献[17]虽然可以取得正确的图像分割阈值, 但耗时较大, 不适用于对图像分割实时性要求高的场合. 因此本文提出改进的DE算法, 采用多种群并行的变异策略, 以提高收敛速度和维持种群多样性. 同时, 再采用自适应的缩放因子和交叉概率以平衡局部搜索和全局搜索. 将本文的改进差分进化算法用于图像分割中阈值的选择, 以最大类间方差作为目标函数进行优化, 并与文献[17]中提出改进的差分进化算法作比较, 实验结果表明本文的算法不仅可以取得正确的分割结果, 而且分割速度更快, 适应于实时性要求高的图像多阈值分割场合.

1 差分进化算法

1.1 经典的差分进化算法

差分进化算法[11]是一种基于群体智能的优化算法,算法利用群体中个体之间的差异信息引导算法进行搜索, 通过变异、交叉、选择三步操作实现种群的进化和优化搜索.

DE算法流程如下: 1) 初始化种群.

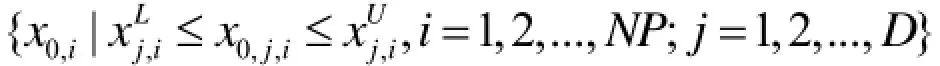
初始种群随机产生:

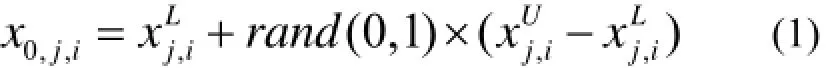
其中,x0,i表示种群中第0代的第i个个体,x0,j,i表示第0代第i个个体的第j个分量.和分别表示第j个分量取值范围的上界和下界.NP表示种群大小,rand(0,1)表示在(0,1)区间均匀分布的随机数.

2) 变异操作. DE通过差分策略实现个体变异, 这也是DE差异进化思想的体现, 其根据当前个体, 在种群中随机选择几个向量进行差分操作并产生一个差分向量, 最常见的差分变异策略有以下五种:

其中xg,i代表种群第g代的第i个个体.i1,i2,i3,i4,i5分别表示从当前种群中随机选择的5个不同的个体.xg,best当前第g代及之前的最优个体,F为缩放因子.

3) 交叉操作. 对第g代个体及xg,i其变异的中间体vg,i进行个体间的交叉操作:

其中,CR为交叉概率,j是正整数且1≤j≤D,D是种群个体最大维数,jrand为1到D的随机整数.

4) 选择操作. DE采用贪婪算法来选择进入下一代种群的个体, 经过变异和交叉操作后生成的试验个体ug,i与xg,i进行竞争. 只有当的ug,i适应度较xg,i更优时才被选作子代; 否则xg,i直接作为子代. 选择操作方程为:

1.2 改进的差分进化算法

为了提高差分进化算法收敛速度和维持种群多样性并克服差分进化算法易早熟、易陷入局部最优的缺点. 本文对缩放因子、变异策略的选择、交叉概率的设置作了改进, 采用多种群并行的变异策略, 自适应选择缩放因子和交叉概率以平衡局部搜索和全局搜索,同时增加了扰动策略, 抛弃适应度低的种群个体.

具体的改进措施见下:

1) 变异策略的选择. 以最大类间方差函数作为适应度函数, 以适应度值排序, 按中值将种群分为两类. ①适应度小的一类选择全局最优变异策略进行变异(式(9)), 加速收敛. ②适应度大的一类迭代前期偏向选择随机变异策略, 迭代后期偏向选择全局最优变异策略(式(10)). 这样前期保持了种群的多样性, 避免局部最优, 后期既加速收敛速度, 也有利于局部精细搜索, 寻找更佳的图像分割阈值组合.

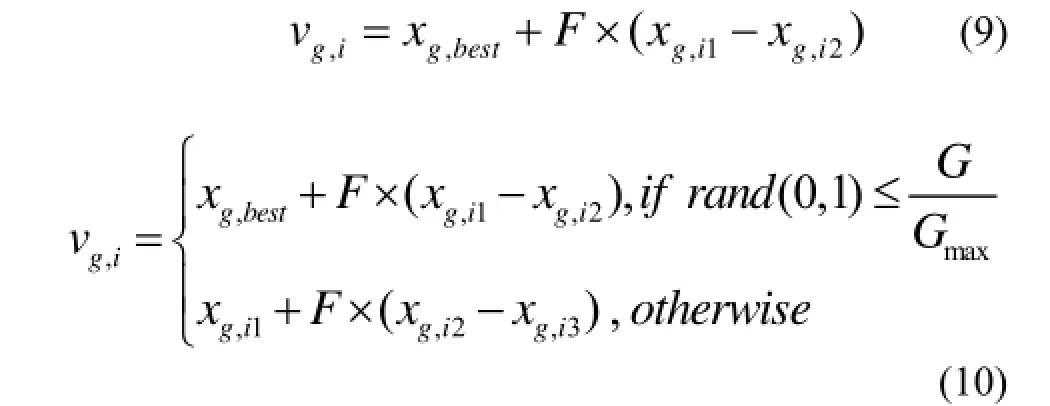
其中,G表示当前的迭代次数,Gmax表示总的迭代次数.F为缩放因子, F较大时能产生较大的扰动, 从而有利于保持种群的多样性, 在图像阈值搜索中更全面, 避免收敛到局部最优值.F较小, 扰动较小, 缩放因子能起到局部精细化搜索的作用. 且文献[19]通过对差分进化算法缩放因子的不同取值策略研究得出开口向上抛物线策略略优于指数策略, 指数策略优于惯性(线性)策略, 而惯性策略优于开口向下策略. 故本文缩放因子采用开口向上抛物线策略, 具体见下式:

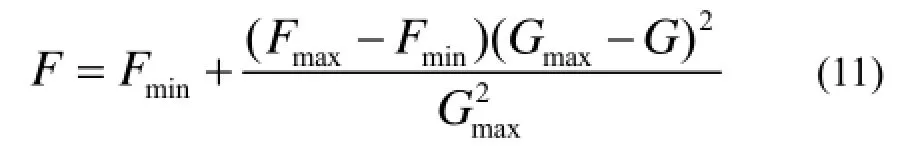
Fmin为最小的缩放因子,Fmax为最大的缩放因子.

2) 交叉概率CR的选择. 较大的CR可以增大交叉概率, 加速收敛, 较小的CR有利于保留最优个体,增强算法鲁棒性. 因此本文采用下式调整CR:

其中,CRmax为最大的交叉系数,CRmin为最小的交叉系数.

3) 新增扰动策略. 对交叉后产生的新种群, 按照适应值大小重新排序, 对适应值最低的两个个体采取抛弃策略, 从种群中剔除, 种群同时重新随进生成新的两个个体进入下一次迭代中.

1.3 改进算法的流程

① 初始化种群, 即随机产生2*N个个体.

② 依据每个个体的适应度大小, 将种群按中值分为两个子种群, 每个种群大小为N.

③ 适应度较高的子种群采用式(10)的变异策略,另一适应度较低的种群采用式(9)变异策略.

④ 在步骤③的基础上两个子群的个体分别进行交叉操作, 交叉概率CR依据式(12)选取.

⑤ 选择. 交叉产生的个体和初始个体中选择保留较优的个体进入下一步.

⑥ 判断是否满足算法终止条件. 若满足, 算法结束, 否则进入步骤⑦.

⑦ 两个子群在步骤⑤产生的个体集中在一起再次依据其适应度大小排序, 抛弃适应度最小的2个个体, 随机生成新的2个个体. 返回步骤②, 算法进入下一次迭代中.

2 实验结果与分析

为了验证本文算法对图像多阈值分割的有效性和运行速度上的优越性, 文章选取了Lenna图、Camera图和Baboon图(图1)作为实验对象进行图像多阈值分割, 并与文献[17]中BDE算法作比较. 实验是在3.30GHz CPU、4G内存的PC机和MATLAB 2012a 环境中进行.

图1 原始图像

依文献[17]所述, BDE算法参数设置如下: 缩放因子F和交叉系数CR按Beta分布自适应选取, 初始种群个体数80, 最大迭代次数40.

文献[20]对DE算法的参数展开了详细的数值分析, 指出了DE算法性能对参数敏感的问题, 这些参数不仅与具体问题相关, 而且它们之间也相互影响. 该文献通过大量实验推荐F初始值为0.6, 交叉系数取值介于0.3～0.9之间. 因此, 本文参数设置如下:Fmin=CRmin=0.3,Fmax=CRmax=0.9. 这样依据式(11),缩放因子F的取值在0.6附近由增递减. 依据式(12),交叉系数CR介于0.3～0.9. 同时经过多次实验初始种群个体数设置为20, 最大迭代次数20.

2.1 图像分割结果比较

每种算法针对不同的图像分别运行10次, 取10次运行结果的平均值作为图像最终分割的结果.

图2 文献[17]BDE算法图像的双阈值分割

图3 本文算法图像的双阈值分割

图4 文献[17]BDE算法图像的三阈值分割

图5 本文算法图像的三阈值分割

图6 文献[17]BDE算法图像的四阈值分割

图7 本文算法图像的四阈值分割

以双阈值、三阈值和四阈值分割为例, 从图2、图3、图4、图5、图6和图7的分割效果看, 不同的算法分割效果几乎一样, 并无明显的不同. 从时间性能比较, 见表1、表2和表3.

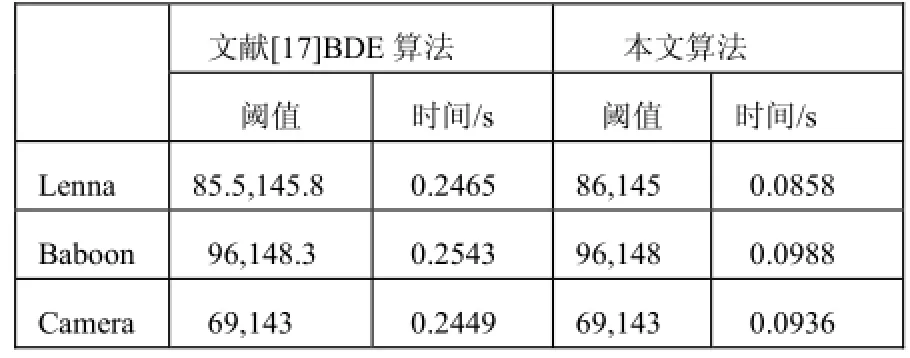
表1 图像的双阈值及运行时间

表2 图像的三阈值及运行时间

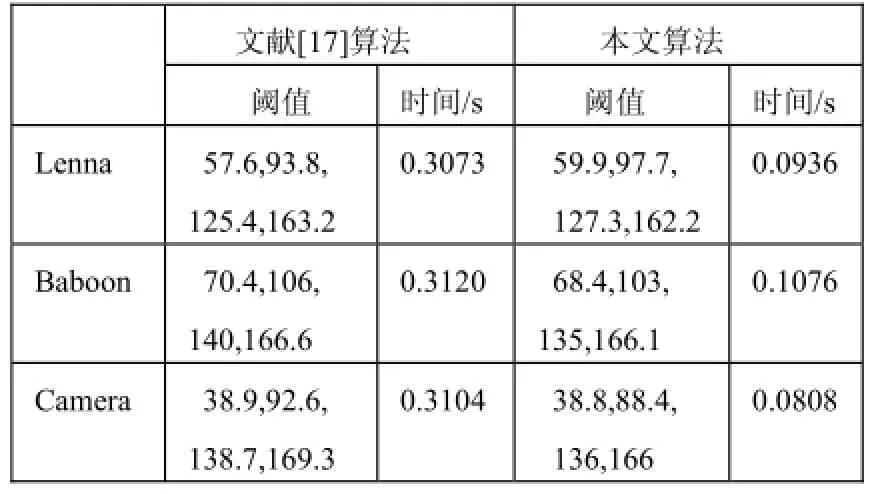
表3 图像的四阈值及运行时间

由表1、表2和表3可知, 所有的分割算法都能取得相似的分割结果, 分割的阈值相近. 但不同的算法分割时间却相差较大. 文献[17]和本文算法对比可知,本文算法的耗时要远远少于文献[17]的算法. 而且文献[17]在双阈值图像分割和三阈值图像分割的运行时间对比, 三阈值的图像分割要比双阈值图像分割的耗时明显多一些. 但本文算法中双阈值、三阈值和四阈值图像分割时间对比可知, 本文算法随着阈值的增加,耗时几乎不变, 这说明本文算法更稳定.

3 结语

本文提出的基于改进的差分进化算法能够充分利用差分进化的特点, 较好的解决了图像多阈值选取过程中计算量大、耗时长的缺点, 提高了图像分割速度,有利于图像的后续处理, 适应于实时性要求高的场合.但本文只考虑了无噪声灰度图像的分割, 因此, 对于彩色图像和含噪声图像的分割是作者今后的研究方向.

1 Otsu N. A Threshold selection method from gray level histogram. IEEE Trans. on System Manand Cybernetics, 1979, 9(1): 62–66.

2 Pun T. A new method for grey-level picture thresholding using the entropy of the histogram. Signal Processing, 1980, 2(3): 223–237.

3 Kapur JN, Sahoop K, Wong AKC. A new method for gray-level picture thresholding using the entropy of the histogram. Computer Vision, Graphics and Image Processing, 1985, 29(3): 273–285.

4 Kittler J, Illingworth J. Minimum error thresholding. Pattern Recognition, 1986, 19(1): 41–47.

5 Tang KZ, Yuan XJ, Sun TK, et al. An improved scheme for minimum cross entropy threshold selection based on genetic algorithm. Knowledge-Based Systems, 2011, 24(8): 1131– 38.

6 杨震伦.闵华清.罗荣华.基于改进量子粒子群优化的多阈值图像分割算法.华南理工大学学报(自然科学版),2015,(5).

7 陈恺,陈芳,戴敏,张志胜,史金飞.基于萤火虫算法的二维熵多阈值快速图像分割.光学精密工程,2014,(2).

8 陈恺,戴敏,张志胜,陈平,史金飞.基于反向萤火虫算法的多阈值缺陷图像分割.东南大学学报(英文版),2014,(4).

9 崔丽群,宋晓,李鸿绪,张明杰.基于改进鱼群算法的多阈值图像分割.计算机科学,2014,(8).

10 尹雨山.王李进.尹义龙.王冰清.赵文婷.徐云龙.回溯搜索优化算法辅助的多阈值图像分割.智能系统学报,2015,(1).

11 Storn R, Price K．Differential evolutiona simple and efficient heuristic for global optimization over continuous spaces. Joumal of Global Optimization, 1997, 11(4): 341–359．

12 邱晓红,江阳,李渤.分形变异因子修正的差分进化算法.模式识别与人工智能,2015,(2):132–138.

13 康忠健,訾淑伟.基于差分进化算法的油田区域配电网无功优化技术的研究.电工技术学报,2014,28(6):226–231.

14 董丽丽,黄贲,介军.云计算中基于差分进化算法的任务调度研究.计算机工程与应用,2014,(5):90–95.

15 Chen N, Chen WN, Zhang J. Fast detection of human using differential evolution. Signal Processing, 2015, 110(2): 155–163

16 Niu Q, Li K, Irwin GW. Differential evolution combined with clonal selection for dynamic economic dispatch. Journal of Experimental & Theoretical Artificial Intelligence, 2015, 27(3): 325–350

17 Ayala HVH, dos Santos FM, Mariani VC, Coelho LdS. Image thresholding segmentation based on a novel beta differentialevolution approach. Expert Systems with Applications, 2015, (42): 2136–2142.

18 高岳林,刘军民.差分进化算法的参数研究.黑龙江大学自然科学学报,2009,26(1):81–85.

19 姜立强,郭铮,刘光斌.仪表、自动化与先进集成技术大会, 2007.

20 Gamperle R, Muller S, Koumoutsakos P. A parameter study for differential evolution. Wseas Int Conf on Advances in Intelligent Systems, Fuzzy Systems, Evolutionary Computation. Interlaken, Switzerland. 2002. 293–298.

Multi-Threshold Image Segmentation Method Based on Improved Differential Evolution Algorithm

YANG Zhao-Long, LIU Bing-Han
(College of Mathematics and Computer Science, Fuzhou University, Fuzhou 350108, China)

The threshold method is a simple and effective image segmentation technique. However, the threshold method also has obvious disadvantage, the amount of calculation for solving threshold appears to be exponential amplification with the increase of threshold. In order to overcome the shortcomings of large computation load and long computation time for multi-threshold image segmentation, we introduce an improved differential evolution algorithm, which proposes a new mutation strategy, adopts self-adaption scaling factor and cross factor, and newly adds Perturbation strategy. In order to achieve multi-threshold segmentation, the improved algorithm considers multi-threshold segmentation as an optimization problem whose objective function is formulated according to Otsu. Experimental results show that compared with other algorithms, the improved algorithm not only can achieve an accurate image segmentation result, but also has a faster speed.

image segmentation; multi-threshold; differential evolution(DE); Otsu; gray image

福建省科技厅项目(2013J01186, JK2010056);福建省教育厅项目(JB10160)

2016-03-30;收到修改稿时间:2016-06-21

10.15888/j.cnki.csa.005537