结合用户聚类和项目类型的协同过滤算法①
王 巧, 谢颖华, 于世彩
(东华大学 信息科学与技术学院, 上海 201620)
结合用户聚类和项目类型的协同过滤算法①
王 巧, 谢颖华, 于世彩
(东华大学 信息科学与技术学院, 上海 201620)
为了解决协同过滤算法中数据稀疏性问题, 提高推荐效果, 提出一种改进的协同过滤算法. 该算法首先通过一种新的相似度计算方法来计算项目类型相似度, 将相似度大于某阈值的项目作为目标项目的邻居; 然后根据目标用户对邻居项目的评分信息来预测该用户对目标项目的评分值, 并将预测值填入稀疏的用户项目评分矩阵; 最后对填充后的评分矩阵采用基于用户聚类(K-means聚类)的协同过滤算法做出最终的预测评分进行推荐.在Movielens 数据集上进行实验验证, 结果表明该算法能够很好地缓解数据稀疏性、降低计算复杂度, 提高推荐精度.
数据稀疏性; 协同过滤; 项目类型; K-means聚类; Movielens 数据集
随着信息技术的迅猛发展, 网络成为人们生活中必不可少的一部分, 其产生的信息数据也呈指数型增长. 面对海量的信息, 用户在选择自己想要的东西时,很难快速抉择, 即产生了“信息过载”[1]现象. 针对该问题, 推荐系统[2]应运而生. 它通过记录用户行为信息,分析得出用户偏好, 然后向用户推荐其可能感兴趣的信息, 避免出现用户不需要的信息, 进而更好地满足用户的个性化需求. 不同的推荐系统对应不同的推荐技术, 最常见的有关联规则[3]、协同过滤技术、神经网络技术、贝叶斯网技术、图模型技术等. 其中应用最广泛最成功的就是协同过滤技术, 尤其是在电商领域中. 协同过滤算法主要包括两方面: 基于模型的协同过滤和基于内存的协同过滤[4]. 基于模型的协同过滤算法不受数据稀疏的影响, 多采用离线建模, 但计算复杂度高, 时效性低. 基于内存的协同过滤算法以用户项目评分为操作基础, 包括基于用户(user-based CF)和基于项目(item-based CF)两种. 该方法简单方便易实现, 因而被广泛采用.
协同过滤算法的基本思想是利用用户项目评分矩阵, 找出与目标用户(项目)相似度最高的K个近邻,利用近邻的评分信息预测目标用户(项目)的评分信息,并将top-N[5]反馈给用户作为推荐. 传统的协同过滤算法在计算相似度时依赖于评分矩阵, 而实际数据中用户评分信息很少, 使得推荐精度大大降低, 这就是所谓的数据稀疏性问题. 此外, 该算法还存在冷启动、扩展性和实时性等问题[6]. 本文针对数据稀疏问题, 先利用项目类型相似性填充用户评分矩阵, 然后对新矩阵基于用户聚类, 不仅缓解了数据稀疏性 , 且聚类技术[7]的使用降低了计算复杂度、节省了时间, 实验证明该改进的算法提高了推荐效果.
1 传统的协同过滤算法
1.1 基于用户的协同过滤算法
使用该算法的前提是认为如果用户的行为属性相似, 那么他们兴趣爱好也就相似, 在选择某商品时他们可能更倾向于同一类, 对商品的评分值也相近. 所以在给目标用户做出推荐时, 可以利用邻居用户的评分信息来对目标用户的评分进行预测. 这种算法思路简单清晰, 主要分三步: 构建用户项目评分矩阵、查找用户邻居、预测评分做出推荐.
① 建立用户项目评分矩阵: 利用用户购买商品的信息建立m×n评分矩阵,m代表用户数,n代表项目数,Rij表示用户i对项目j的评分值. 评分值的范围通常在1—5之间, 为整数数值表示, 当没有评分信息时通常以0代替.
② 寻找邻居用户: 利用评分矩阵计算用户间的相似度, 得出与目标用户最相似的K个最近邻居.
③ 预测评分做出推荐: 根据邻居用户对目标项目的评分预测目标用户对该项目的评分值, 作出Top—N 项目推荐列表. 预测评分计算公式: 假设N(u)=(u1,u2,L,uk)为目标用户的最近邻居集,则用户u 对未评分项目i的预测评分Pu,j[8]可表示为:

其中,sim(u,v)表示目标用户u与用户v的相似度,表示用户v对项目i的实际评分,表示目标用户u在所有已评分项目中的平均评分,表示邻居用户v在所有已评分项目中的平均评分.
1.2 相似性计算方法
最常见的相似度计算方法有三种: 相关相似性(也称Pearson系数相关性)、余弦相似性和修正的余弦相似性[9].
① 相关相似性: 在用户共同评过分的项目集上,计算两者的皮尔森相关系数, 即为相似度. 其计算公式如下所示.

② 余弦相似性: 通过计算两评分向量夹角的余弦值, 来度量用户间的相似度, 夹角越小相似度越大.其计算公式如式(3).
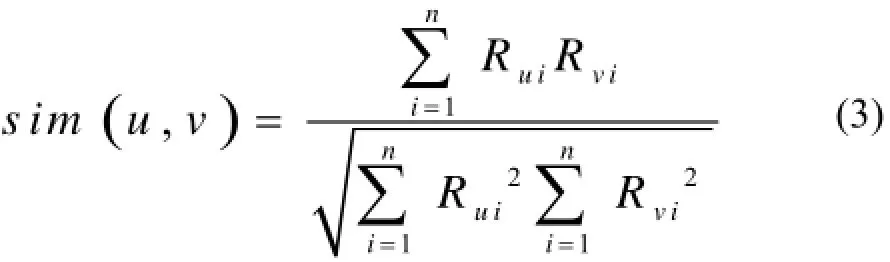
③ 修正的余弦相似性: 每个人的评分标准和尺度不一样, 比如说A非常喜欢某项目, 他会给出4分的评价; 而B也非常喜欢该项目, 他会给出5分的评价.从评分数据来看,B比A更喜欢该项目, 但实际上A的喜好程度不亚于B, 这是因为两者的评分标准不同.针对该问题, 提出修正的余弦相似性计算方法, 即将余弦相似性中的向量减去用户平均评分向量后再计算夹角余弦值. 其计算公式如式(4)所示.

以上3个公式中Rui表示用户u对项目i的评分值,表示用户v对项目i的评分,表示用户u的平均评分,表示用户v的平均评分,表示用户u和v共同评过分的项目集合,Iu、Iv分别表示用户u、v的评分项目集,n是用户u、v共同评过分的项目数.
2 本文改进的结合用户聚类和项目类型的协同过滤算法
为了解决传统算法中的数据稀疏问题, 本文提出了一种结合用户聚类和项目类型的协同过滤算法, 即先利用项目类型相似性来填充稀疏的评分矩阵, 然后再用基于用户聚类的协同过滤算法对新矩阵计算预测评分, 产生推荐.
2.1 算法步骤:
第一步: 填充稀疏的评分矩阵
① 计算项目相似度, 查找邻居
把两项目相同类型个数与两项目具有的类型总数的比值作为项目相似度的计算方法. 若项目i具有的类型个数为n1, 项目j具有的类型数为n2, 项目i和j共同具有的类型数为n, 则两者的相似度计算公式为:

设定阈值, 若项目相似度sim(i,j)大于该值, 即为目标项目的邻居.
② 根据目标用户对邻居项目的评分信息预测目标用户对该项目的评分值, 将预测值填充稀疏的评分矩阵.
预测评分计算公式:
当用户u对邻居项目j的评分为0, 且不为零时,该公式的分子为:
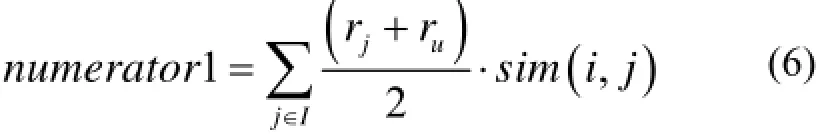
当用户u对项目j的评分不为0时, 则公式的分子为:

则用户u对未评分项目i的预测评分为:
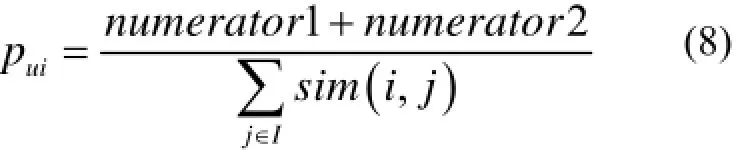
其中表示目标用户u的平均评分,表示用户对项目j的平均评分,表示用户u对项目j的评分值,I为项目i的邻居集.
第二步: 对新矩阵进行基于用户聚类
协同过滤技术中经常使用聚类算法来缓解数据稀疏性, 降低计算复杂度, 提高系统实时性. 聚类就是将一个庞大的群体按照某种特征分为若干个小群体,使群内成员具有较高的相似度, 群与群之间差别较大.该算法适合大规模的数据集, 在电子商务网站中使用尤为普遍. 其中K-means聚类法由MacQueen[10]首先提出, 是目前使用最多的聚类算法. 该算法把小群体称之为簇, 每个小群体内的成员互为邻居. 本文使用K-means聚类法先对新矩阵基于用户聚类, 然后再寻找邻居进行预测推荐.
① K-means聚类步骤
a.先在数据集中随机选择出K个元素作为聚类中心; b.计算其余元素与聚类中心的距离, 并将该元素划分到与其距离最小的簇中(一个聚类中心代表一个簇); c.取每个簇中所有元素的均值作为新的K个聚类中心; d.若聚类中心变化, 重复步骤b和c, 直至聚类中心不再变化或者收敛公式小于某一值.
其中距离计算方法有多种: 如明科夫斯基距离、曼哈顿距离、切比雪夫距离、欧式距离[11]. 本文使用最常用的欧氏距离法, 公式为:
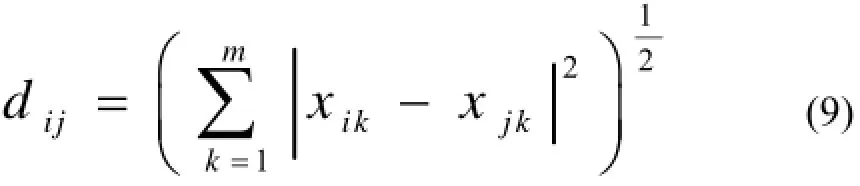
公式中dij表示元素i和j之间的距离, 两个元素集合分别为:

K-means聚类法使用距离平方和最小作为聚类收敛准则, 表达式为:
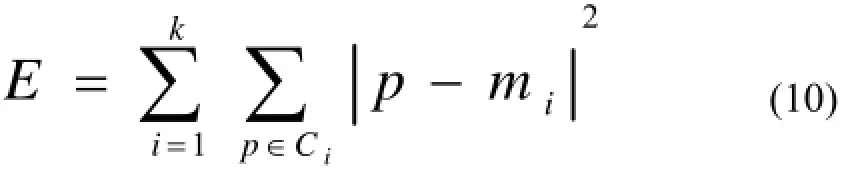
表达式中p代表数据集中待分配的元素,m表示簇的中心点,C表示簇.
② 寻找邻居进行预测推荐
a. 根据新的评分矩阵, 使用上述K-means聚类法将用户分为若干簇.
b. 计算目标用户与每个簇中心的距离, 找到距离最小相似度最大的一个或若干个簇.
c. 在这些相近的簇中计算每个用户与目标用户的相似性.
d. 根据Top-N或阈值法选出目标用户的n个邻居用户. Top-N法是将与目标用户相似度最大的前N个用户作为邻居; 阈值选择法是把相似度大于某个阈值的用户选为邻居. 本文实验中采用Top-N法确定用户邻居.
e. 预测评分做出推荐. 根据用户邻居对目标项目的评分信息, 加权平均预测目标用户对目标项目的评分值, 并根据预测结果做出推荐.
2.2 改进算法的分析
本文算法首先根据项目本身类型, 找到邻居项目,然后根据目标用户对邻居项目的评分值, 计算其对未评分项目的评分值, 并将其填充原评分矩阵, 得到一个较为稠密的评分矩阵. 该法克服了数据稀疏性问题,还在新项目冷启动方面起到了一定的缓解作用. 传统的基于项目的协同过滤算法依赖于评分值计算项目相似度, 评分值的稀疏性使得对同一项目评分的用户数量很少, 影响着相似度计算精度; 而该算法采用新的公式计算项目相似度, 完全不受评分值的影响, 提高了相似度计算精度. 很多研究学者采用矩阵降维法、平均值填充等方法来填充稀疏的矩阵, 相对于这些方法来说, 该算法计算简单, 且充分考虑了项目类型信息, 有着较强的可行性. 然后, 对新矩阵操作时引入聚类技术. 通过聚类, 大的用户集合变为若干个小的用户集合, 在查找目标用户的邻居时, 不需要对每个用户操作, 只需在与目标用户相近的一个或若干个簇中计算簇内元素与目标用户的相似度. 并且, 聚类的过程可以离线完成, 在线只是查找邻居进行预测推荐,这就减少了计算复杂度, 节省了时间和空间, 提高了推荐实时性.
3 实验设计与结果分析
3.1 实验数据集
在协同技术研究中, Movielens数据集被广泛使用,权威性较强. 本文采用的数据是从该数据集随机抽取的100, 000条评分记录, 包含943个用户对1682部电影的评估, 其中每个用户都至少评论了20部影片. 电影共有19个类型,每部电影可以同时具有多种类型;用户评分共有5个等级(1-5), 评分越高, 则用户的喜好程度越大. 评分矩阵的稀疏度计算公式为: 评分矩阵中没有评分值的个数/总的评分记录数; 则该数据集的稀疏性为1-100000/(943×1682)=0.93695. 该实验数据集包括训练集和测试集, 比例为4:1.
3.2 实验度量指标
本实验中,采用MAE(平均绝对误差)对算法的精度进行评估.若预测评分集合为实际评分集合为则用户u预测的MAE[12]表达式为:
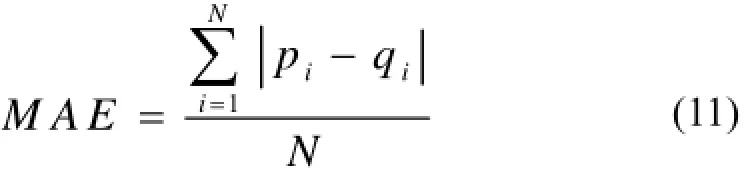
MAE是根据预测评分值和实际评分值之间的偏离程度来计算预测精度的,MAE值越小, 与真实值相差越小, 预测精度越高, 推荐效果越好.
3.3 实验结果与分析
本文实验在Movielens数据集上进行, 训练集和测试集为4:1, 共有5组数据进行重复实验, 最后将5组实验的均值作为最终的结果.
在填充稀疏的评分矩阵时, 为了保证评分矩阵不被过分优化, 影响推荐精度, 经过多次试验选取项目相似度阈值为0.6, 将相似度大于该值的作为目标项目的邻居, 低于该值的舍弃. 这个阈值相当于项目A有8个类型, 项目B有8个类型, 项目A和B共同具有的类型数是6个, 只有2个类型不同, 可见大于该阈值的项目具有较高的相似性. 这也保证了预测值的可靠性,不至于出现填充过优, 推荐背离的现象.
本实验在查找用户邻居时引用了聚类技术来降低计算复杂度, 聚类数影响推荐效果, 根据已有研究学者的结论, 通常聚类数为7时具有较低的MAE值, 推荐效果较好[13]. 所以, 本实验中先使用聚类数7来进行验证.
① 相似度比较
在聚类数为7的条件下, 通过5次实验, 邻居数从10到60, 分别对相关相似性、余弦相似性和修正的余弦相似性进行实验, 计算其MAE值, 结果取5次实验的平均值, 如下图1所示.

图1 三种相似度对比图
由图1可以观察到, 随着邻居数的增加, 三条折线都呈下将趋势. 其中余弦相似性MAE值最高, 修正的余弦相似性次之, 相关相似性MAE值最低.MAE值越低, 与真实值越接近, 预测精度越高, 所以, 接下来的实验均采用相关相似性进行用户相似度的计算.
用户相似度计算结果部分截图如图2所示, 从图中可以看到相似度值范围为-1到1. 其中0代表不相关;负值表示负相关, 即用户兴趣爱好相反; 正值表示正相关, 且相似性大小跟数值大小成正比.
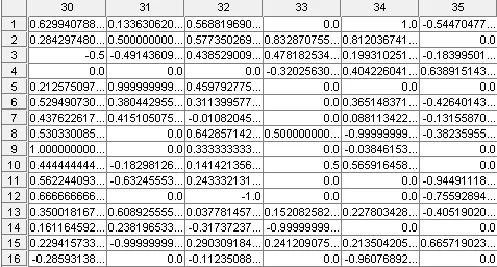
图2 用户相似度部分截图
② 聚类数的选择
为了验证聚类数7是比较理想的选择, 我们在上述结论的条件下, 使用相关相似性, 分别对聚类数6、7、8进行实验, 用户邻居范围选为10—60, 结论如图3.3所示. 由实验结果可以得出, 同等条件下, 聚类数为7时MAE值最低, 即聚类数7是本实验最好的选择,因此下面实验均采用聚类数7进行.

图3 聚类数的选择对比图
③ 本文算法与传统的协同过滤算法结果对比
为了验证本文提出算法比传统的协同过滤算法具有更好的推荐效果, 在①和②的结论下, 取聚类数7,相关相似性计算法, 邻居数10—80, 分别对两种算法进行实验, 画出结果图如下所示.
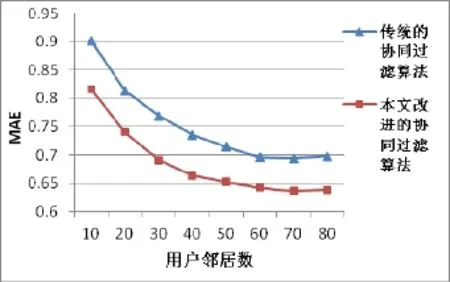
图4 本文算法与传统的协同过滤算法结果对比
由图4可以看出, 本文算法MAE值较小, 表明本文算法具有优越性, 能够提高推荐质量.
4 小结
本文首先介绍了协同过滤算法的实现过程和存在的不足, 然后针对稀疏性问题提出改进的结合用户聚类和项目类型的协同过滤算法, 并通过一系列实验,证明了该算法的优越性. 主要工作为: a、针对评分矩阵的稀疏性问题, 本文有效地利用项目类型相似性,根据用户对邻居项目的评分预测其对未评分项目的评分值, 并将其填充原矩阵, 得到较为稠密的新的用户评分矩阵. b、传统的协同过滤算法依赖于评分值计算项目相似度, 而评分矩阵的稀疏性严重影响着项目相似性计算的精度. 本文提出的改进的算法, 有效地利用项目属性信息, 采用新的项目相似度计算公式, 简单可行, 不依赖于评分值, 避免了“相似而不相同”现象的出现, 且对新项目冷启动问题起到了一定的缓解作用. c、本文算法对新矩阵先聚类用户, 然后在簇内查找邻居, 降低了近邻查询空间和计算复杂度, 提高了系统实时性. 最后在Movielens数据集上验证了该算法的优越性.
1 蔺丰奇,刘益.信息过载问题研究述评.情报理论与实践, 2007,30(5):710–714.
2 刘建国,周涛,汪秉宏.个性化推荐系统的研究进展.自然科学进展,2009,19(1):1–15.
3 索琪,卢涛.基于关联规则的电子商务推荐系统研究.哈尔滨师范大学自然科学学报, 2005,21(2):50–53.
4 段玮.基于协同过滤的个性化推荐算法研究[硕士学位论文].武汉:华中科技大学,2009.
5 Liu DR, Shih YY. Hybrid approaches to product recommendation based on customer lifetime value and purchase preferences. The Journal of Systems and Software, 2005, 77 (2): 181–191.
6 曾小波,魏祖宽,金在弘.协同过滤系统的矩阵稀疏性问题的研究.计算机应用,2010,30(4):1079–1082.
7 张亮.基于聚类技术的推荐算法研究[硕士学位论文].成都:电子科技大学,2012.
8 Hyung JA. A new similarity measure for collaborative filtering to alleviate the new user cold-starting problem. Information Sciences, 2008, 178(1): 37–51.
9 黄正.面向数据稀疏的协同过滤推荐算法研究与优化[硕士学位论文].广州:华南理工大学,2012.
10 MacQueen J. Some methods for classification and analysis of multivariate observations. The 5th Berkeley Symposium on Mathematical Statistics and Probability. 2015, 1. 281–297.
11 黄洋.基于聚类和项目类别偏好的协同过滤推荐算法研究[硕士学位论文].杭州:浙江理工大学,2013.
12 Papagelis M, Plexousakis D. Qualitative analysis of user-based and item-based prediction algorithms for recommendation agents. Engineering Application of Artificial Intelligence, 2005, 18(7): 781–789.
13 袁利.基于聚类的协同过滤个性化推荐算法研究[硕士学位论文].武汉:华中师范大学,2014.
Collaborative Filtering Algorithm Combined with the User Clustering and Item Types
WANG Qiao, XIE Ying-Hua, YU Shi-Cai
(School of Information Science and Technology, Donghua University, Shanghai 201620, China)
In this paper, in order to solve the problem of data sparseness and improve the effect of recommendation, an improved collaborative filtering algorithm is put forward. Firstly, this algorithm calculates the item-types similarities through a new calculation method and the items whose similarities are greater than a certain threshold value will be considered as neighbors of the target-item. Secondly, the system predicts target-user’s score values for the target-item according to the scores for the neighbors of target-item, and the predicted values will be filled in the sparse score matrix. Finally, this algorithm clusters the new matrix (K-means clustering) based on the users, to predict target-user’s score values and make recommendations. The experimental results on the Movielens dataset show that this algorithm can effectively alleviate the data sparseness, reduce the computational complexity and improve recommendation accuracy.
data sparseness; collaborative filtering; item-types; K-means clustering; Movielens dataset
2016-03-14;收到修改稿时间:2016-04-27
10.15888/j.cnki.csa.005478

