30% SiCp/Al复合材料热变形及动态再结晶行为
孙亚丽, 谢敬佩, 3,郝世明,王爱琴, 3,柳培,李敏
30% SiCp/Al复合材料热变形及动态再结晶行为
孙亚丽1, 谢敬佩1, 3,郝世明2,王爱琴1, 3,柳培1,李敏1
(1. 河南科技大学材料学院,洛阳 471023;2. 河南科技大学物理与工程学院,洛阳 471023;3. 有色金属共性技术河南省协同创新中心,洛阳 471023)
采用Gleeble-1500D热模拟试验机研究30% SiCp/Al复合材料在温度为623~773 K、应变速率为0.01~10 s−1下的热变形及动态再结晶行为。结果表明:材料的高温流变应力−应变曲线主要以动态再结晶软化机制为特征,峰值应力随变形温度降低或应变速率升高而增大,材料热激活能为272.831 kJ/mol。以试验数据为基础,建立-和¶/¶-曲线,从而进一步获得动态再结晶的临界应变和稳态应变,通过试验数据的回归分析,建立动态再结晶的临界应变模型和稳态应变模型,并在此基础上,获得所需要材料的动态再结晶图。
30% SiCp/Al复合材料;热变形;动态再结晶;临界应变;稳态应变
碳化硅颗粒增强铝基复合材料因具有密度低、比强度高、耐高温、耐磨损、热膨胀系数低等优异性能,在航空航天[1−2]、汽车、电子科技等领域拥有广阔的应用前景。其中SiC体积分数为30%~45%的碳化硅颗粒增强铝基复合材料因其比刚度、尺寸稳定性等功能化特性更为突出,成为航空航天领域惯性器件的原材料,被誉为“第3代航空航天惯性器件材料”[3]。迄今为止,国内外学者对于铝基复合材料及铝合金的热变形行为进行了大量研究。赵明久等[4]研究了17% SiCp/2024Al复合材料在温度为573~773 K、应变速率为0.02~0.5 s−1变形条件下的热变形行为,得到不同温度区间内不同的激活能;李红章等[5]认为位错增强粒子周围塞积而密度增加,使得材料内部能量整体分布不均匀,利于再结晶形核。故在较高温度下,复合材料的软化行为以动态再结晶为主,且增强颗粒会阻碍亚晶界和晶界迁移,提高复合材料发生动态回复所需临界应变,使材料积蓄足够位错储能而诱发动态再结晶。张鹏等[6]通过建立-和¶/¶-曲线,获得15% SiCp/Al复合材料动态再结晶的临界应变;YOO等[7]通过分析15% SiCw/AA2124复合材料的流变应力和压缩后的显微组织确定其变形机制,并运用-关系曲线计算出动态再结晶临界应变。LIA等[8]分析了2519铝合金在温度为350~450 ℃之间的热变形,其在应变速率为0.01~1 s−1时发生动态回复,而在应变速率为10 s−1时则发生动态再结晶。关于对30% SiCp/ 2024Al复合材料的热变形和动态再结晶行为的研究却鲜有报道。热模拟作为研究材料高温变形行为的一种有效手段,近年来已广泛应用。高温变形能力通常与变形温度、变形速率和变形程度有关。在不同的变形条件下,材料的变形能力和微观组织不同,材料的变形区域分为失稳区和稳定变形区[6],失稳区常常出现增强颗粒的开裂、颗粒与基体界面的分离以及基体的开裂等失效方式。稳定变形区为加工优选区域,是发生动态再结晶的区域,因此,本实验重点研究SiCp/ Al复合材料的热变形及动态再结晶行为。
1 实验
实验材料为30% SiCp/Al复合材料,增强体材料粒度为3.5 μm的SiCp粉末,形状为不规则尖锐多角块状。基体材料为采用超音速喷射沉积法制成的2024Al合金粉末,原始粒度为10 μm。成分配比为30% SiC+70%Al(体积分数),原料混合均匀后,在VDBF- 250真空热压烧结炉中进行烧结。图1所示为30%SiCp/Al复合材料的显微组织,组织较为致密,无明显孔隙;灰色相为Al基体,灰黑色颗粒相为SiC,白色相为基体中的Al-Cu合金相。表1所列为该复合材料的性能指标。

图1 30%SiCp/Al复合材料的微观结构
热压缩试样是直径为8 mm、高为12 mm的圆柱体,利用Gleeble-1500D热模拟试验机沿轴向对试样进行热压缩,研究复合材料的高温热变形行为,采用圆柱体单向压缩法。实验前,在试样的两端均匀涂敷润滑剂(石墨+机油),使端面受力均匀,以减少试样端面的摩擦力对试验精度的影响。变形温度分别为623,673,723和773 K;应变速率分别为0.01,0.1,1和10 s−1,压缩应变量为0.5。变形后立即水淬,保留热变形组织便于观察分析。

表1 30% SiCp/Al复合材料性能测试结果
2 结果与讨论
2.1 真应力−应变曲线
图2所示为不同应变速率下的应力−应变曲线。在整个变形过程中,流变应力随应变量增加呈现先增大后减小的趋势,这是加工硬化和动态回复、再结晶软化共同作用的结果。在变形的初始阶段,加工硬化作用占主导地位,材料的流变应力迅速增加;随变形量增加,材料将发生动态再结晶。当加工硬化作用和软化作用达到平衡时,应力−应变曲线出现1个应力峰值。随后再结晶软化作用占据主导地位,材料的应力逐渐降低,最后达到1个稳定值保持不变。随变形温度升高和应变速率降低,晶界的可移动性有所增加,积累畸变能以及位错湮灭的时间有所延长,因此,有利于动态再结晶等软化行为发生[9]。
当变形开始后,加工硬化率急剧增加到峰值,随变形量增加,加工硬化率逐渐减小,达到零值,即为峰值应力p,这是由于金属材料的变形机理是位错滑移,金属加工硬化通常认为是在塑性变形过程中,空间晶格产生畸变所引起的。金属空间晶格的畸变会阻碍滑移的进行,畸变越严重,塑性变形越难进行,加工硬化率越大。但是,加工硬化率并不是随变形程度增加而一直增大,在材料发生加工硬化的同时,变形产生的位错能够通过交滑移和攀移等方式运动,使部分位错消失,部分位错重排,从而造成金属材料的回复软化。当材料内部的位错通过塞积与增殖积累到一定临界密度即变形达到临界应变后,会诱使动态再结晶发生。
不同温度和不同应变速率下的峰值应力如表2所列。由表2可知:当应变速率恒定时,流变应力随温度升高而降低。这是由于随着温度升高,材料动态再结晶的形核率和长大速率增加,软化作用增强;而且温度越高,原子动能越大,原子间的结合力越弱,即剪切应力降低。可见,30% SiCp/Al复合材料是温度敏感材料。
由表2还可知,在恒定温度下,流变应力随应变速率增加而增大。因为在恒定温度下,应变速率较低时,再结晶形核时间较长,形核数量增多,再结晶软化作用强于加工硬化作用。随应变速率增加,变形组织形核和长大概率减少,导致位错增殖急剧增加,加工硬化作用更加明显,表现为流变应力迅速升高。可见,30% SiCp/Al复合材料对应变速率具有正的敏感性:即温度越高,应变速率越小,材料变形抗力越小,复合材料达到稳态变形就越容易。
2.2 热变形本构方程
金属材料的高温塑性变形过程和高温蠕变过程相似,都存在热激活过程,流变应力取决于变形温度和应变速率,在不同的应力水平下可以用以下方程来描述[10]:
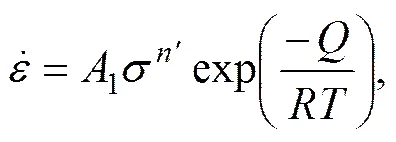
,>1.2 (2)
(3)
式中:1,2,,,,和都为材料常数;常数,和之间满足/;为应变速率,单位为s−1;为变形温度,单位为K;为气体常数;为材料的热变形激活能,单位为kJ/mol。

图2 30% SiCp/Al复合材料热压缩变形真应力−应变曲线
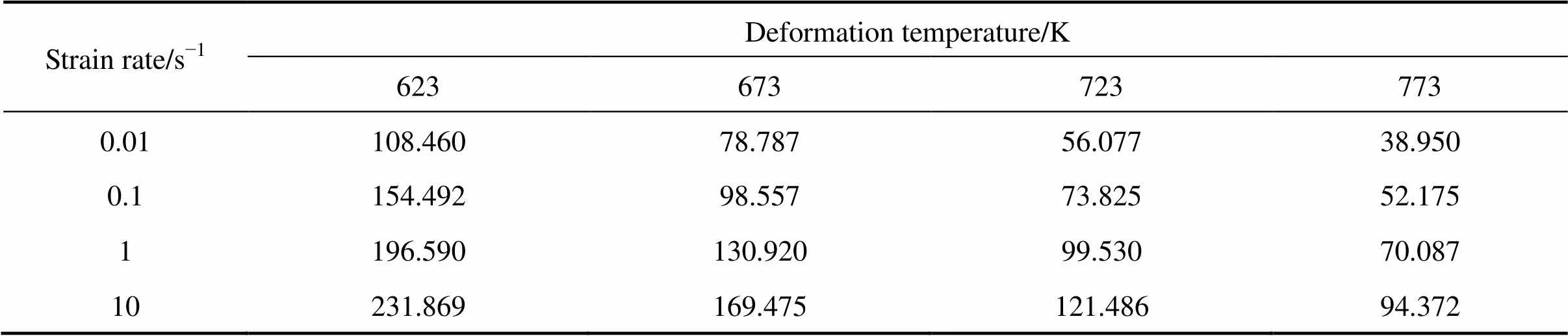
表2 不同温度和不同应变速率下的峰值应力
SELLARS 和TEGART等[11]提出并实验验证了热变形条件,通常可以用温度补偿的应变速率因子Zener- Hollomon参数[12]表示:

对式(1),(2)及(4)进行自然对数运算,可得:
(5)

(7)
图3及图4所示为30% SiCp/Al复合材料峰值应力与应变速率之间的关系图。
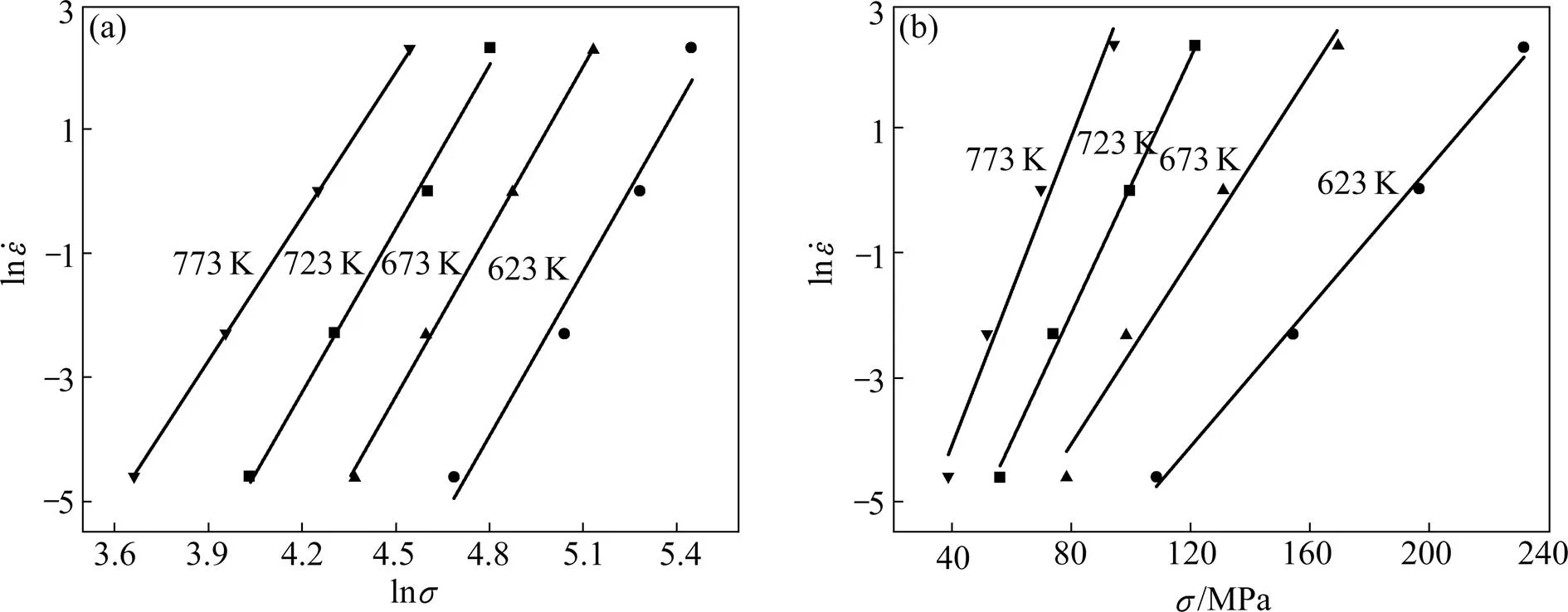
图3 峰值应力和应变速率的关系

图4 峰值应力、应变速率、变形温度的关系

30% SiCp/Al复合材料的热变形激活能==272.831 kJ/mol。由与,可求得对应ln,绘制ln[sinh()]−ln图,如图5所示。其截距ln= 44.5。将所求参数代入式(3)中,即可求得30% SiCp/Al复合材料的高温热变形本构方程:
(9)

图5 30% SiCp/Al复合材料峰值应力与Z参数的关系
为了验证所求方程的准确性,利用热模拟试验的数据对本构方程进行验证,图6所示为应变速率分别为0.01 s−1和0.1 s−1时复合材料峰值应力计算值与实测值的对比。从图6可以看出:峰值应力实测值与计算结果相对误差分别为3.687%和1.42%,吻合度较高,表明本构方程的建立,可为实际生产提供理论依据。

图6 30%SiCp/Al复合材料峰值应力计算值与实测值比较
2.3 动态再结晶的临界条件
在一般情况下,真应力−应变曲线是材料形变时微观组织的外在表现,真应力−应变曲线出现峰值表示材料内部组织发生了动态再结晶,而真应力−真应变曲线并不能直接反映材料何时、何种变形程度开始发生动态再结晶。在临界应变条件下,发生动态再结晶取决于材料的基本化学成分和热变形参数。POLIAK[13]等认为动态再结晶的发生需要满足2个条件:最大的储存能和最小的耗散速率,
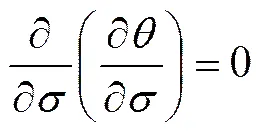
则动态再结晶开始的临界点能够直接由-曲线确定。本实验即采用POLIAK[13]提出的再结晶临界条件来确定30% SiCp/Al复合材料的动态再结晶临界应变。依据式(10)对热模拟实验数据进行计算得到不同变形条件下的-曲线和¶/¶-曲线,分别如图7和图8所示。结合图7中的拐点和图8中极小值可以确定临界应力(c)、峰值应力(p)、临界应变(c)和峰值应变(p)。
图7 不同变形条件下30% SiCp/Al复合材料的-曲线
Fig.7 The-curves of 30% SiCp/Al composite under different deformation conditions (a) 623 K; (b) 673 K; (c) 723 K; (d) 773 K
由图7可知,该复合材料的-曲线在各个温度和应变速率均出现拐点。如图7(a)所示,当应变速率为10 s−1时,出现明显拐点,拐点处对应的应力为临界应力。为了更加精确地描述曲线中拐点位置,对-曲线求一阶偏导可得到-¶/¶-曲线,如图8(a)所示。图中各-¶/¶-曲线上的最小值所对应的流变应力即为发生动态再结晶所对应的临界应力c,而流变曲线上与临界应力相对应的应变即为发生动态再结晶的临界应变c。随应变速率增加,图7中各曲线拐点愈加明显,如图7(b)~(d)所示;图8(b)~(d)则均出现对应最小值。对比图8中各图可以看出,临界应力和峰值应力随温度的升高和应变速率的降低而降低。
不同条件下的临界变c和峰值应变p及其比值见表3。从表3可知:发生动态再结晶的临界应变与峰值应变的平均比值为c/p=0.725,随应变速率提高,临界应变和峰值应变都相应提高。这是由于动态再结晶新晶核的形成都需要靠位错的迁移、合并,使小角度结晶形成大角度晶界。当材料以较小的应变速率变形时,晶粒内部产生位错有足够的时间进行迁移、合并,形成大角度晶界。而当应变速率升高时,晶粒内部位错没有足够的时间进行迁移,这需要增加变形量提高位错密度,从而使动态再结晶临界应变增加。随变形温度升高,临界应变和峰值应变降低。这是由于变形温度升高,位错迁移驱动力增大,位错更加容易迁移,使材料在较小的变形条件下就能形成动态再结晶新的晶粒。
为了构建30% SiCp/Al复合材料变形过程中临界应变预测模型,目前广泛使用Sellars模型[14]:c=aZ。式中:和均为常数;为Zener-Hollomom参数;=为应变速率,为热变形激活能,为气体摩尔常数。结合所求的热变形激活能,可以建立各热变形条件下的临界应变与其相对应的,绘制lnc-ln关系图,如图9所示。由图9可见:lnc与ln之间呈现较高的线性关系,对其进行线性拟合,可得拟合方程:lnc=0.079ln−6.62,即临界应变预测模型可表示为c=1.32×10−30.079。
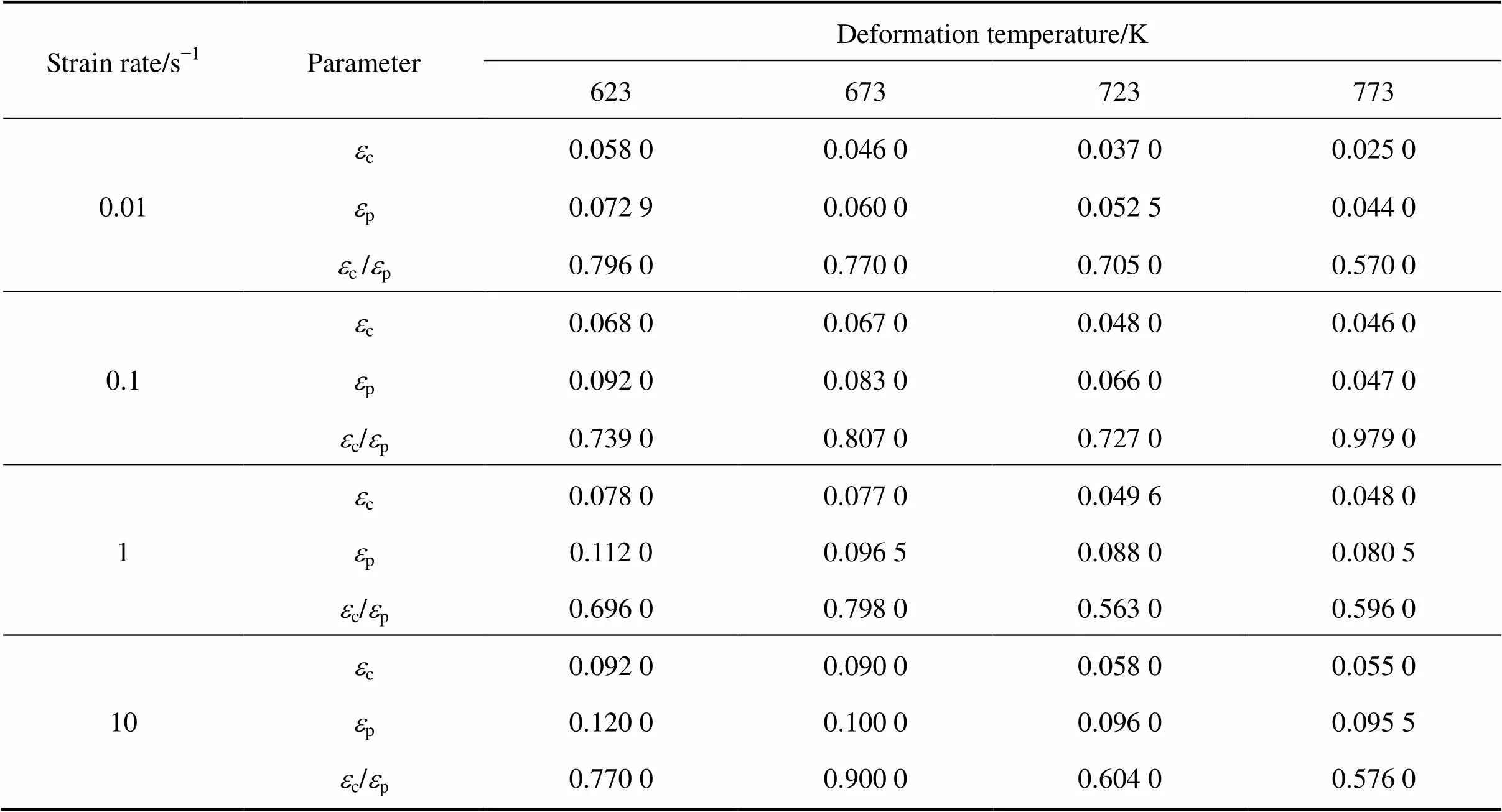
表3 不同条件下的临界应变ec和峰值应变ep及其比值

图8 不同变形条件下30% SiCp/Al复合材料的-¶q/¶s-s曲线
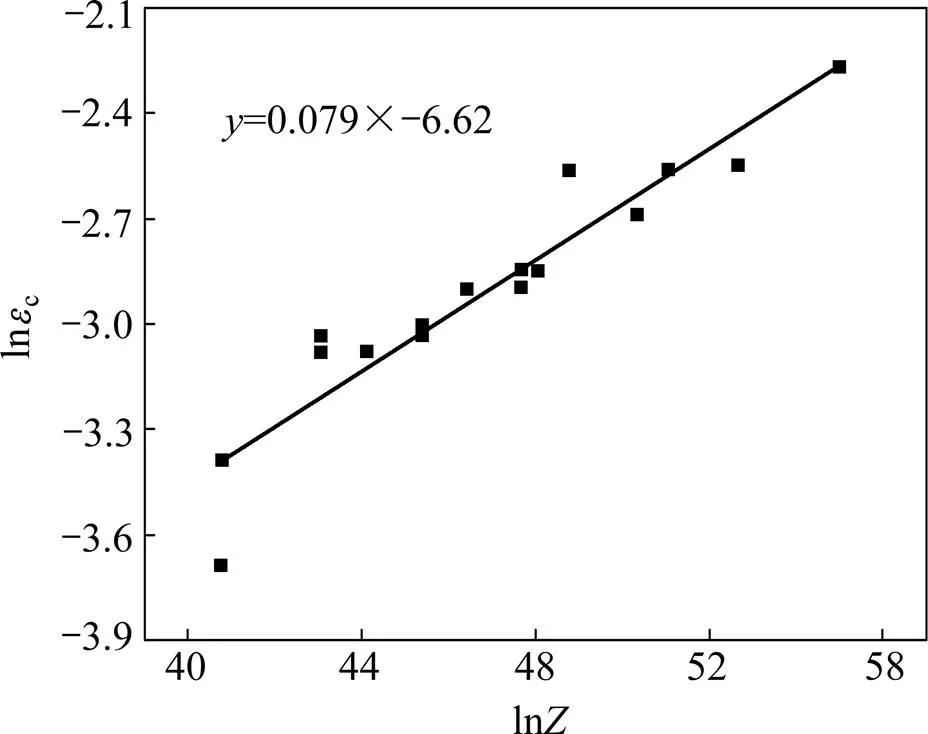
图9 lnec与lnZ之间的关系
2.4 动态再结晶图的建立
动态再结晶图的建立是为了准确了解再结晶过程发生的区间,而要确定这个图形,需要2个应变量:临界应变c与稳态应变ss。其中,稳态应变ss可根据加工硬化率−应变()获得,该材料的曲线如图10所示。由图10可知:在达到极大值后又迅速减小,当第1次为0时所对应的应变为峰值应变;随应变继续增加,又继续减小为负值;当达到极小值后又增加到0,此时所对应的应变为稳态应变ss。
稳态应变一般用以下模型来描述:ss=BZ,其中,和为常数。与计算临界应变处理方法相似,可绘制lnc-ln关系图,如图11所示。可得临界应变表达式为:ss=0.50640.006。
将临界应变c与稳态应变ss放在同一幅图中,并观察它们与ln的关系,如图12所示,该图即为动态再结晶图。从图12可以看出:随增加,发生动态再结晶的临界应变与稳态应变均呈增大趋势,图中有I,II和III 3个区域,分别代表未发生动态再结晶区,部分发生动态再结晶区和完全发生动态再结晶区。临界应变主要集中在0.05附近,并且临界应变c与ln的拟合曲线比较陡,说明ln对c的影响较弱;而稳态应变ss的分布区域要大一些,并且拟合曲线较为平缓,说明ln对ss的影响更大一些。

图10 不同应变速率下的加工硬化率−应变(θ−ε)曲线
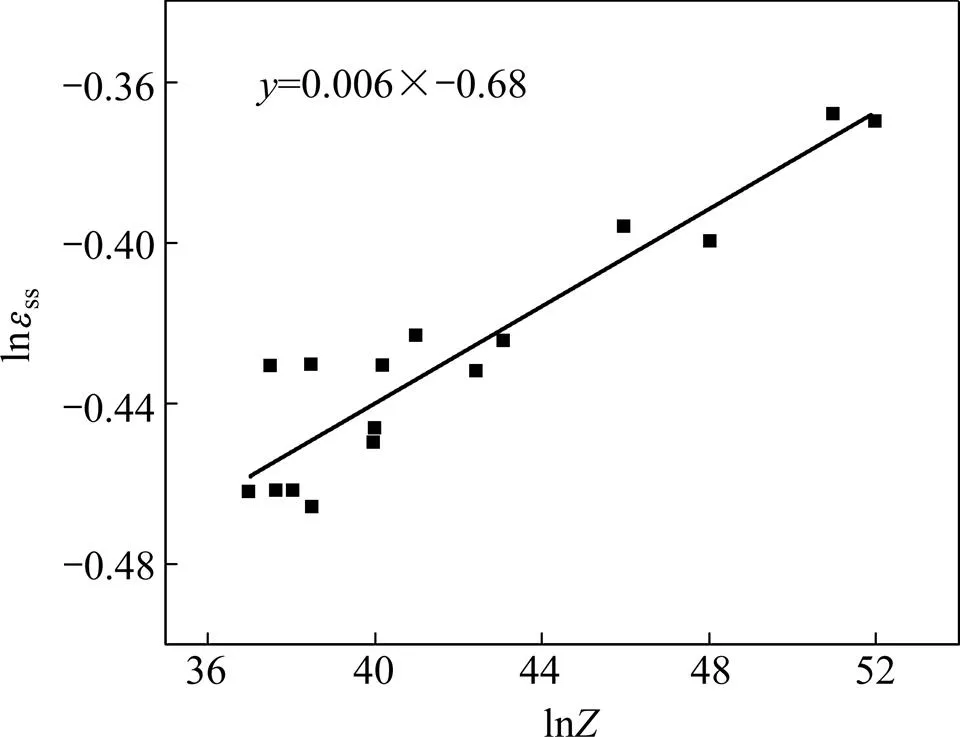
图11 lness与 lnZ之间的关系

图12 动态再结晶图
2.5 30% SiCp/Al复合材料显微组织的转变
从微观角度分析,在热变形初期阶段,材料内部位错密度逐渐增加,对应的流变应力也逐渐增大。在热激活能的作用下,位错的交滑移和攀移容易进行,位错容易在滑移面间转移,而使异号位错相互抵消,结果使位错密度下降,畸变能降低,不足以达到动态再结晶所需的能量水平,动态回复一般是高层错能金属热变形过程中常见的软化机制。
若不发生动态再结晶,则该复合材料会进入稳态变形阶段。这时由位错增殖所引起的应变硬化与位错交滑移、攀移等动态回复所引起的软化达到动态平衡,表现在真应力−应变曲线上是1条平行于横轴的直线。然而,实际情况是30% SiCp/Al复合材料的流变应力随应变的增加呈下降趋势(如图2所示),这表明随变形进行,该材料的软化已强于硬化,出现了动态再结晶。
图13所示为应变速率为1 s−1时,不同温度下的显微组织。由图13可知:随变形温度升高,基体内的晶界处出现动态再结晶晶粒。这是因为晶界处能够同时具备大角度晶面和高密度缺陷2个再结晶形核的基本条件,具有较高的变形能,是再结晶优先形核和长大的部位,形成细小、等轴的再结晶组织;随变形温度升高,细小、等轴再结晶晶粒将代替原来的被拉长的晶粒;在变形温度为673 K时,原始组织中的大晶粒被严重拉长,部分大晶粒晶界周围有细小的再结晶晶粒出现,表明此时动态再结晶开始形核;在723 K时,少量被拉长的变形大晶粒夹杂在细小的等轴再结晶晶粒中,出现混晶组织。

图13 在=1 s−1,不同变形温度时30% SiCp/Al复合材料的变形组织
对铝基复合材料而言,由于大量的增强颗粒存在,造成第二相粒子对晶界具有强烈的钉扎作用,不仅降低了晶界的可移动性,而且限制了在高温状态下晶粒难于长大,在很大程度上限制了动态再结晶过程的形成。但对于基体金属而言,由于第二相粒子尺寸很大,其间距较宽(一般大于1 μm),所以容易导致在基体金属表面产生再结晶核心能,常常造成基体金属的再结晶过程发生。
3 结论
1) 30% SiCp/Al复合材料的热变形过程中以动态再结晶机制为主要软化机制,峰值应力随变形温度降低或应变速率升高而增加,该材料为温度和应变速率敏感材料。根据流变应力、应变速率和变形温度的关系,计算出30% SiCp/Al复合材料高温热压缩时的热变形激活能为272.831 kJ/mol,建立了流变应力本构方程:
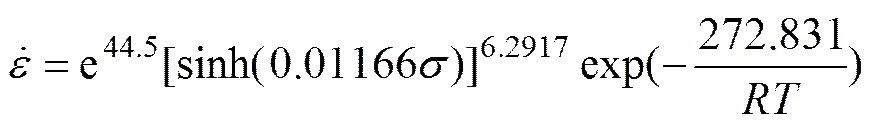
2) 30% SiCp/Al复合材料发生动态再结晶时,其-曲线出现拐点,并且在-¶/¶-曲线上出现最小值。利用此拐点判据,可以确定材料的动态再结晶临界条件。动态再结晶临界应变随着应变速率的增大及变形温度的降低而增加,且临界应变与峰值应变之间具有相关性:c/p=0.725。
3) 在本实验条件下,引入参数能较好地反映临界应变与热变形条件之间的变化规律。临界应变c随参数的增加而增大,且二者之间函数关系为:c= 1.32×10−30.079。
4) 利用曲线可以确定发生动态再结晶后的稳态应变,结合临界应变绘制出了动态再结晶图。
REFERENCES
[1] OMYMA E K, FATHY A. Effect of SiC particle size on the physical and mechanical properties of extruded Al matrix nanocomposites[J]. Materials and Design, 2014, 54(2): 348−353.
[2] XIONG B, XU Z, YAN Q, et al. Effects of SiC volume fraction and aluminum particulate size on interfacial reactions in SiC nanoparticulate reinforced aluminum matrix composites[J]. Journal of Alloys and Compounds, 2011, 509(4): 1187−1191
[3] 郝世明, 谢敬佩. 30% SiCp/2024A1复合材料的热变形行为及加工图[J]. 粉末冶金材料科学与工程, 2014, 01(19): 1−7. HAO Shiming, XIE Jingpei. Hot deformation behavior and processing map of 30% SiCp/2024A1 composite[J]. Materials Science and Engineering of Powder Metallurgy, 2014, 1(19): 1−7.
[4] 赵明久, 刘越, 毕敬. 碳化硅颗粒增强铝基复合材料(SiCp/ 2024Al)的热变形行为[J]. 金属学报, 2003, 39(2): 221−224. ZHAO Mingjiu, LIU Yue, BI Jing. Hot deformation behavior of silicon carbide particulate reinforced 2024 aluminum-based composite[J]. Acta Metallurgica Sinica, 2003, 39(2): 221−224.
[5] 李红章, 张辉, 陈振华, 等. 7075Al/SiCp复合材料的热压缩变形流变应力和组织行为[J]. 材料导报, 2006, S1: 271−272+284. LI Hongzhang, ZHANG Hui, CHEN Zhenhua, et al. Flow stress and structure behavior of 7075Al/SiCpcomposites during hot compression deformation[J]. Materials Review, 2006, S1: 271−272+284.
[6] 张鹏, 李付国. SiC颗粒增强Al基复合材料的动态再结晶模型[J]. 稀有金属材料与工程, 2010, 39(7): 1166−1170. ZHANG Peng, LI Fuguo. Dynamic recrystallization model of SiC particle reinforced aluminum matrix composites[J]. Rare Metal Materials and Engineering, 2010, 39(7): 1166−1170.
[7] YOO Y C, JEON J S, KO B C. Hot deformation and dynamic recrystallization of SiCw/AA2124 composites[J]. Materials Science Forum, 1996, 217−222: 1157−1162.
[8] LIA H Z, WANG H J, LIANG X P, et al. Hot deformation and processing map of 2519A aluminum alloy[J]. Materials Science and Engineering A, 2011, 528(3): 1548−1552.
[9] 曹宇, 邸洪双, 张洁岑, 等. 800H合金动态再结晶行为研究[J]. 金属学报, 2012, 10(48): 1175−1185. CAO Yu, DI Hongshuang, ZHANG Jiecen, et al. Research on dynamic recrystallization behavior of incoloy 800H[J]. Acta Metallurgica Sinica, 2012, 10(48): 1175−1185.
[10] 刘勇, 孙永伟, 田保红, 等. 20% Mo/CuAl2O3复合材料的强化机理及热变形行为[J]. 中国有色金属学报, 2013, 23(3): 750−756. LIU Yong, SUN Yongwei, TIAN Baohong, et al. Strengthening mechanism and hot deformation behavior of 20%Mo/CuAl2O3composite[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(3): 750−756.
[11] SELLARS C M, TEGART W J M. On the mechanism of hotdeformation[J]. Acta Metallurgica, 1996, 14(09): 1136−1138
[12] 马博, 彭艳, 刘云飞, 等. 低合金钢Q235B动态再结晶动力学模型[J]. 材料热处理学报, 2010, 31(04): 141−145.MA Bo, PENG Yan, LIU Yunfei, et al. Dynamic recrystallization kinetics model of low- alloy steel Q345B[J]. Transactions of Materials and Heat Treatment, 2010, 31(4): 141−145.
[13] Pollak E I, Jonas J J. Initiation of dynamic recrystallization in constant strain rate[J]. ISIJ International, 2003, 43(5): 684−691.
[14] XU Yaowen, TANG Di, SONG Yong, et al. Prediction model for the austenite grain growth in a hot rolled dual phase steel[J]. Materials and Design, 2012, 36(1): 275−278.
(编辑 高海燕)
Hot deformation and dynamic recrystallization behavior of 30% SiCp/Al composite
SUN Yali1, XIE Jingpei1, 3, HAO Shiming2, WANG Aiqin1, 3, LIU Pei1, LI Min1
(1. School of Materials Science and Engineering, Henan University of Science and Technology, Luoyang 471023, China; 2. School of Physics and Engineering, Henan University of Science and Technology, Luoyang 471023, China;3. Collaborative Innovation Center of Non-Ferrous Materials of Henan Province, Luoyang 471023, China)
Using Gleeble-1500D simulator, the high-temperature plastic deformation behavior and dynamic recrystallization behavior of 30% SiCp/Al composite were investigated at 623−773 K with strain rate of 0.01−10 s−1. The results show that the high-temperature flow stress-strain curves of the composite has softening characteristics of the dynamic recrystallization, and the peak stress increases with the decrease of deformation temperature or the increase of strain rate. Based on the true stress-strain curves, the activation energy of the composites is 272.831 kJ/mol. In the study,-and¶/¶-curves are plotted based on the experimental data to furtherly obtain the critical strain and steady-state strain of DRX. Then the critical strain model and the steady-state strain model of DRX are set up by regression analysis of experimental data. Based on the results, the diagram of DRX for 30% SiCp/Al composite was given.
30% SiCp/Al composite; hot deformation; dynamic recrystallization; critical strain; steady-state strain
TB333
A
1673−0224(2016)01−8−10
国家自然科学基金资助项目(51371077);河南科技大学重大科技项目培育基金(2015ZDXM01)
2014−12−03;
2015−01−20
谢敬佩,教授,博士。电话:0379-64277396;E-mail: Xiejp@haust.edu.cn

