频域磁声耦合成像逆问题初步研究
张顺起 马 任 周晓青 殷 涛 刘志朋
(中国医学科学院 北京协和医学院 生物医学工程研究所,天津 300192)
频域磁声耦合成像逆问题初步研究
张顺起 马 任 周晓青 殷 涛 刘志朋#*
(中国医学科学院 北京协和医学院 生物医学工程研究所,天津 300192)
对频域磁声耦合成像方法逆问题进行初步研究,为实现基于频域处理方法的磁声电导率成像打下基础。应用复平面矢量方法,基于声源和频域幅值相位特性,研究频域磁声成像逆问题数学模型和重建方法。对频域磁声信号随声源空间位置和幅度变化特性进行仿真,对简单模型不同声源分布的频域逆问题进行仿真重建。建立多频率下的声源幅值和相位矢量方程组,利用非线性方程组的优化算法求解声源信息。利用铜丝仿体,对矢量求解方法和逆问题声源重建进行实验验证。频域幅值和相位满足复平面声源矢量叠加理论。利用矢量方法,初步实现两个声源样本的声源幅度和位置的重建,成像分辨率小于1 cm,实验的声源重建位置误差小于±0.4 mm。通过对频域磁声成像逆问题的重建研究,为后续进行复杂模型和真实组织的频域磁声重建研究打下基础,对实现高分辨率成像具有重要研究意义。
磁声耦合成像;频域;矢量法;逆问题;重建
引言
磁声成像技术是新型的生物组织电特性成像技术[1-2],基本原理如图1所示,对置于稳恒磁场中的介质施加电流激励,电流受到洛仑兹力作用,使介质中带电粒子发生振动,在介质仿体外检测到声波响应[3]包含了组织的电导率信息。基于磁声耦合效应的无损功能成像方法,同时具有电阻抗成像高对比度[4-5]及超声成像高空间分辨率[3]特点,对肿瘤等疾病的早期诊断具有重要的研究价值[6]。
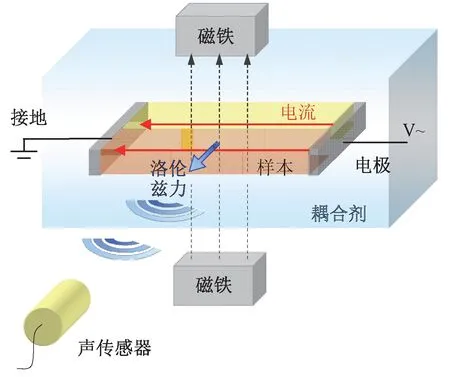
图1 磁声耦合成像原理Fig.1 Principle of magneto-acoustic imaging
磁声耦合成像方法仍实验室研究阶段,国内外有家研究小组在此领域开展工作[7-9]。目前磁声成像主要基于提高脉冲激励特性与检测方式以获得高空间分辨率,仿真中将激励理想化为冲激函数进行有限元建模[10-12],计算磁声信号并进行图像重建[13-14]。然而实际应用时激励源使用10 kV级高压微秒脉宽的短脉冲[7,15],设计实现具有难度,不仅造价较高,而且安全性存在隐患。同时,脉冲信号携带声源信息持续时间段平均功率低、信噪比较低、检测精度低,限制了成像质量。本研究提出基于连续波激励的频域磁声成像方法,旨在降低激励源性能要求,提高检测精度和信噪比[16-17]。传统时域重建算法不适用于频域检测成像,频域磁声耦合逆问题重建是频域磁声成像研究中的关键内容。
本研究工作基于磁声耦合成像原理,利用矢量法求解磁声信号频域幅值相位,研究由频域幅值相位重建声源的频域磁声成像逆问题,初步实现声源图像重建,探索连续波激励下的磁声成像新方法。
1 理论
1.1 频域磁声耦合成像方法的数学建模
频域磁声耦合波动方程[8]为
(1)式中:S(jω)为施加于成像样本上的激励函数的频谱;H(jω)为磁声成像系统函数的傅里叶变换。F为介质质点受到的洛伦兹力密度,F=J×B0,J为电流密度,F和J均为空间分量。B0为静磁场,c为介质中的声速。
利用频域格林函数求解,根据分离变量法[7],得到的频域磁声压信号表达式为
(2)式中:Gk(r,r0)=ejω|r-r0|/c/(4π|r0-r|)为格林函数;根据欧姆定律J=σE,声源项包含介质电导率信息;ejω|r-r0|/c为延迟项,反映介质中各质点到达检测器形成的相位延迟,该参数体现为频域相位;1/(4π|r0-r|)为声波在距离上的传输系数,由频域幅值体现。
利用式(2),即可实现频域磁声信号的求解。
1.2 频域幅值相位的矢量法求解
为提高磁声信号在频域内检测精度和成像分辨率,考虑到频域内正弦连续波为冲激函数,便于进行频内单一频率的检测,因此采用正弦信号进行激励。
根据电路理论的矢量分析方法[18],正弦信号s(t)=A1sin(ω1t+ω1t1)可表示为矢量形式eA1+jω1t1,其实部为A1cos(ω1t1),虚部为A1sin(ω1t1),因此介质样本内每一点声源信号,均可由一矢量表示,大小为矢量半径,到达检测器的时间延迟为矢量的相位角。若将式(2)的积分化为求和形式,则由介质样本发出的磁声信号为各声源矢量在复平面求和,有
(3)
其中
(4)
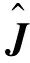
对于第i个声源,其实部虚部分别为
(5)
对于整个样本,为n个点声源的总和,则由频域测量方法获得的幅值和相位分别为
(6)
1.3 频域磁声逆问题重建
频域磁声逆问题,即由频域声信号幅值和相位重建介质声源分布。考虑一个简单介质模型,设介质有n层界面,传感器指向性理想化为仅检测传感器轴线附近声场,各层界面平行于传感器端面,各层声源幅值为ai,距离为li(i=1,2,…,n),设激励信号的频率为ω1,设频率ω1下测量的声信号幅值为AMP1,相位为PHA1,ai、li为未知量。为重建2n个未知量,需建立2n个方程,因此选择n个频率ω1,ω2,…,ωn下进行测量,获得n个关于幅值、n个关于相位的方程,进行频域逆问题求解,有
(7)
利用非线性方程组的优化算法[19-20]进行计算,即可实现频域磁声耦合逆问题的声源重建。
2 方法
2.1 仿真方法
为了对频域磁声求解方法进行验证,首先对单层和多层介质的不同位置声源的幅值相位进行仿真,分析频域幅值、相位随声源变化的对应规律。在此基础上,对不同声源的位置和强度进行逆问题求解。
2.1.1 仿真装置
根据式(2),洛伦兹力密度散度不为零处即有声源产生,为了分析声源形成磁声信号的频域特性,以垂直于传感器轴线方向的电导率界面声源作为研究对象,设电流沿x方向,静磁场沿z方向,则洛伦兹力沿-y方向,如图1所示。
2.1.2 仿真参数设置
由前所述,为了提高频域信号锁相放大测量精度,选择连续正弦信号进行激励。根据式(2),声信号穿过距离产生的传播时间延迟,反映在频域的相位变化上,设相位为PHAi,对应的传播距离li,正弦激励周期为T,频率f,则声源到传感器的距离与相位延迟之间的对应关系为
(8)
可见,频域磁声信号的相位与激励频率成正比。频率越高,相位对尺寸灵敏度越高。同时考虑到避开生物组织骨骼运动、呼吸等产生的声频率[2],选择激励频率应在1~2 kHz以上。
另一方面,实际测量中锁相放大角度范围为-180°~180°,为避免多周期相位重复引起的混淆,应使激励信号波长大于成像介质长度,即频率和成像空间应满足
lif≤c
(9)
考虑到人体软组织声速约1 460 m/s,人体腹部成像深度在几十cm之内,激励频率选择kHz。在本研究中,选择了10和20 kHz作为激励频率。
2.2 实验方法
(五)PPP融资模式的使用,可以在一定程度上提高建设项目的质量,增强品质,能够实现政府与企业两者利益上的共享。PPP项目是政府与企业共同进行的,能够与政府进行合作,说明企业一定有自身的实力,包括建设项目的经验和技术等,而建设项目的质量直接关系到企业的获益情况,所以必定会全力以赴。同时,政府对PPP项目付费时,会根据建设项目的质量要求进行付费,倘若达不到建设项目原定计划的要求,则会对建设项目的经费进行一定的扣除。这种现象其实在PPP项目开始之前,政府和企业之间就对项目的收益分配情况进行了协商,这样不仅能够确保双方的利益不会受损,还能够有效避免利益分配不均问题的出现。
为了验证频域逆问题重建方法,本研究利用频域磁声成像实验系统,首先检测多组声源及其叠加后的频域声信号幅值、相位,验证复平面矢量求解方法,在此基础上对双导线声源进行逆问题重建实验。
频域磁声成像实验系统的主要结构如图2所示。函数发生器产生激励波形,由功率放大器放大,样本置于0.3 T静磁场中。声传感器由步进电机控制定位,定位精度小于1 mm。声信号由预极化传声器(MP201)获取,经锁相放大器(LI5640)放大[21],再用采集卡(PXI4462)采集存储。系统由Labview虚拟仪器平台进行总体控制。

图2 频域磁声成像实验检测系统Fig.2 Experimental system of magneto-acoustic imaging in frequency domain
3 结果
3.1 仿真结果
3.1.1 两层声源位置变化的频域信息仿真
设两层声源a、b,幅度均为1 kg·m-3·s-2,距离检测器距离分别为la、lb,同时变化时,设激励频率10 kHz,幅值和相位的变化特性如图3所示。
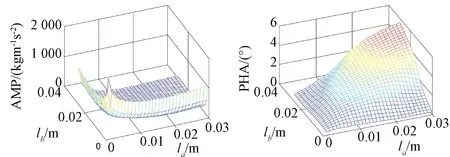
图3 激励频率10kHz时,声源a、b与检测器距离同时变化时产生的声信号。(a)频域声压幅值曲面;(b)相位曲面Fig.3 Generated sound signal when the distance from the sonic source a, b to the detector changes at the same time. The excitation frequency is 10 kHz. (a) The sonic source amplitude surface in frequency domain; (b) The phase surface
由图3中可见,对于2层边界声源,在一个周期(0.1 ms),对应长度(0.034 m)范围内,不同位置的声源,对应不同的幅值和相位信息,幅值和相位曲面连续可微,为后续建立多频率下非线性方程组,实现逆问题声源位置的求解,进行图像重建提供了依据。
3.1.2 声源重建的仿真结果
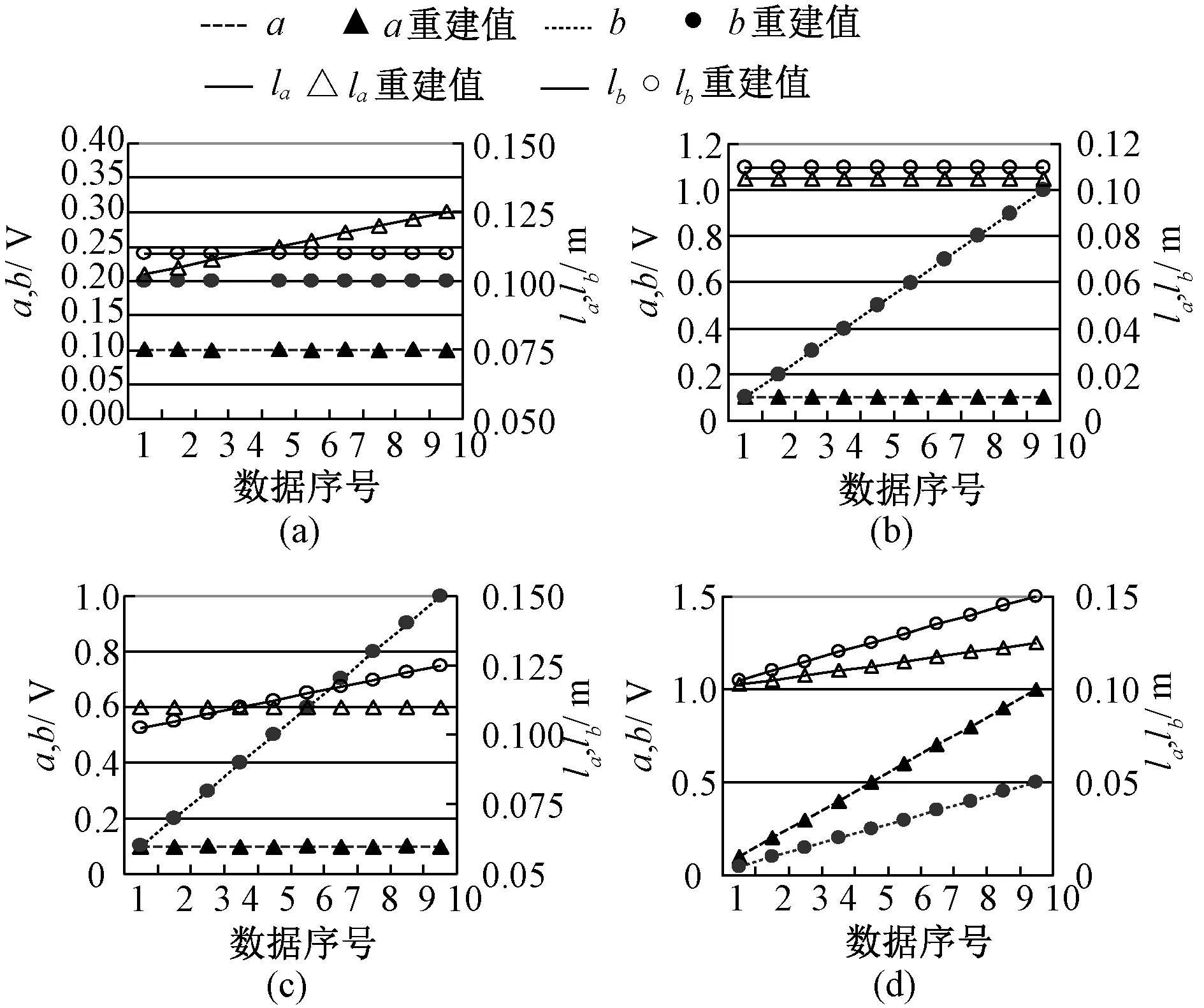
图4 双边界介质的声源重建结果。 (a)令b改变,其余参数不变的重建结果; (b)令lb改变,其余参数不变的重建结果; (c)令b,lb改变,其余参数不变的重建结果及误差; (d)令a,b,la,lb同时改变的重建结果及误差Fig.4 Sonic source reconstruction results of two layered medium. (a) Reconstruction result when b changes, and other parameters unchanged; (b) Reconstruction result when lb changes, and other parameters unchanged; (c) Reconstruction result when b and lb changes, and other parameters unchanged; (d) Reconstruction result when a,b,la and lb changes
图4表明声源幅值、相位重建值与初始值相符合,本研究的重建方法可实现2层平行介质边界声源的位置及幅值的重建,计算可知重建相对误差均在10-7以下。
对不同厚度和电导率的矩形介质进行重建,设介质厚度为2.5,5,7.5,…,25 mm,同时各介质对应的内层电导率对应声源幅值分别为0.05,0.1,0.15,…,0.5 kg·S-2·m-3,如图5(a)所示,采用频域逆问题重建算法进行重建,重建结果如图5(b)所示。
由图5可见,对于不同厚度介质、不同电导率值的矩形平行声源介质,可通过本重建算法实现两层介质声源的重建。
3.2 实验结果
3.2.1 金属仿体频域幅值相位检测实验
实验中通过对间隔相同的4根铜丝加载相同激励电压,幅值1 V,频率为10和20 kHz,分别检测各导线产生的声信号的幅值相位。4根铜丝分别作为声源,由近及远分别命名为a、b、c、d,间隔均为5 mm,检测器距离为0.1 m。

图5 不同厚度和电导率矩形介质的重建 (坐标轴单位:mm;每行从左至右的介质厚度为2.5~25 cm, 以2.5 cm递增;介质电导率边界对应的声压幅值为0.05~0.50 kg·s-2·m-3,以0.05 kg·s-2·m-3递增)。(a) 原始电导率分布;(b) 重建的电导率Fig.5 Reconstruction to rectangle medium with different thicknesses and conductivities. (Axis units : mm; Thickness of the media from left to right are 2.5~25 cm, with 2.5 cm increments; Conductivity boundary corresponding to a sound pressure amplitude of 0.05~0.5 kg·s-2·m-3 with 0.05 kg·s-2·m-3 increments). (a) The original conductivity distributions; (b) The reconstructed conductivity distributions
表1显示了采用声传感器接收声压并转换为电压的测量值,以及与理论计算结果对比,理论计算通过单根仿体频域幅值和相位在复平面内平行四边形求和法则得到。表1中1~4行a、b、c、d表示单独检测各声源的幅值及相位测量值,5~13行中a+b表示声源a、b同时存在时的测量值,以此类推。

表1 多根铜丝声源实验结果
由表1多根铜丝仿体的实验检测结果可见,测量得到的磁声信号的幅值和相位,与理论结果基本相符,其幅值误差在±10%以内,相位误差在±10°以内,误差主要由于系统噪声以及测量误差引起的。利用重建算法计算可知,该误差引起的重建幅值误差在±13%以内,长度误差在±1.1 mm以内。该结果与仿真重建结果对比可见,信号检测精度对声源的重建和成像起重要作用,通过设置噪声屏蔽装置等方法,减小测量误差,可进一步使得重建误差减小,提高重建精度。同时可见,对于声源a+b形成的频域幅值和相位与b+c形成的频域幅值和相位结果可见,由于距离间隔相等,其幅值和相位的变化满足空间移动5 mm后的幅值相位,即空间多声源的同步移动可视为其总体声源的空间移动,对应复平面矢量的整体转动,实验结果验证了复平面矢量方法。此外,表1中可见由10和20 kHz频率激励下获得的声信号幅值和相位结果不同,进一步为逆问题求解提供依据。
3.2.2 基于频域信号的图像重建初步研究
为了验证频域重建方法,实验中采用相邻为5 mm的两根铜丝作为成像仿体,激励为1 V,频率为10和20 kHz分别进行激励,采用步进电机驱动声传感器进行横向移动,记录不同位置的结果,对结果校准后,将其代入重建算法,得到不同位置的声源分布,见图6。

图6 铜丝声源重建结果。(a)铜丝照片; (b)重建图像Fig.6 Sonic source reconstruction result. (a) Photograph of the copper wire; (b) The reconstructed image
由图6可见,重建声源与原始分布近似,分辨率小于1 cm,重建的声源位置误差小于±0.4 mm。
4 讨论
前期研究表明[22],采用频域测量的磁声成像检测处理方法,激励源输出幅度可降低为1 mA。同时,基于连续波激励相关研究表明[16],连续波激励比脉冲形式激励,信噪比可获得显著提高。因此,利用本研究的频域磁声成像逆问题求解方法,将有利于实现磁声成像信噪比提高和降低激励源输出的性能要求。
笔者对提出的频域逆问题的理论和求解方法进行了初步研究,尚存在需进一步解决的问题,列举如下。
第一,理论方面,目前进行了有限边界正逆问题研究,对于多层边界以及未知边界数量的复杂情况下的逆问题,还有待进一步研究。可考虑结合脉冲方式,或结合超声成像及其他激励模式,在此基础上建立正问题模型,并进行频域磁声成像测量和逆问题重建。
第二,实验重建目前还存在一定误差,其主要原因在于实验装置的散射和反射使得信号存在误差,空间噪声对待测信号产生干扰,导致测量引入误差。同时,由于金属仿体本身,无法保证理想的直线和平行。该误差可通过改进实验系统,进行噪声吸收去除模块,减小噪声的影响,实现重建精度的提高。同时金属丝作为实验样本距离真实生物组织存在较大差异。下一步将应采用模拟生物组织仿体或真实生物组织进行实验测试,研究该方法的适用性。
第三,频域方法灵敏性高,但测量稳定性有待加强。可考虑适当降低激励频率,同时设置噪声屏蔽装置,在提高测量稳定性的同时,减小噪声影响。
5 结论
本研究提出了一种基于复平面矢量的频域磁声成像逆问题数学模型和重建方法,并通过仿真和实验对频域磁声成像问题进行探讨。基于复平面矢量方法,对频域磁声信号幅值相位求解以及声源重建方法进行了研究。通过仿真计算了不同声源分布的频域幅值相位特性,对不同位置和幅度的声源进行了仿真重建。结果表明,利用本研究建立的频域磁声逆问题重建方法,可实现简单形状介质样本的初步重建,分辨率小于1 cm。本研究为后续复杂模型和真实组织的频域磁声重建打下基础,对实现高分辨率成像具有重要意义。
[1] Han Wen. Volumetric Hall effect tomography [J]. Ultrasound Imaging, 1999, 21: 186-200.
[2] Bradley JR. The role of magnetic forces in biology and medicine [J]. Experimental Biology and Medicine. 2011, 236: 132-137.
[3] 万明习. 生物医学超声实验 [M]. 西安:西安交通大学出版社, 2010: 20-38.
[4] 徐桂芝. 生物医学电阻抗成像技术 [M]. 北京:机械工业出版社, 2010: 20-32.
[5] 董秀珍. 生物电阻抗成像研究的现状与挑战 [J]. 中国生物医学工程学报, 2008, 27(5): 641-643;649.
[6] Hu Gang, Erik C, He Bin. Magnetoacoustic imaging of human liver tumor with magnetic induction [J]. Applied Physics Letters, 2011, 98: 023703.
[7] Xu Yuan, He Bin. Magnetoacoustic tomography with magnetic induction (MAT-MI) [J]. Institute of Physics Publishing, 2005, 50: 5175-5187.
[8] Xia Rongmin, Li Xu, He Bin. Reconstruction of Vectorial Acoustic Sources in Time-Domain Tomography [J]. IEEE Trans Med Imaging, 2009, 28(5): 669-675.
[9] 张顺起, 殷涛, 马任, 等. 注入电流式磁声成像的电导率模型构建和实验研究 [J]. 中国生物医学工程学报, 2011, 30(6):801-806.
[10] Wang Shigang, Zhang Shunqi, Ma Ren, et al. A study of acoustic source generation mechanism of magnetoacoustic tomography [J]. Computerized Medical Imaging and Graphics, 2014, 38(1): 42-48.
[11] 李珣. 基于乳腺肿瘤模型的感应式磁声成像正问题研究[J]. 中国生物医学工程学报, 2010,3(29): 390-398.
[12] Grasland-Mongrain P, Mari J M, Chapelon J Y, et al. Lorentz force electrical impedance tomography[J]. Irbm, 2013, 34(4-5): 357-360.
[13] 李珣, 朱善安. 基于时间反演方法的三维磁感应磁声成像电导率重建[J]. 中国生物医学工程学报, 2009, 28(1): 48-52.
[14] Sun Xiaodong Zhang Feng, Ma Qingyu, et al. Acoustic dipole radiation based conductivity image reconstruction for magnetoacoustic tomography with magnetic induction [J]. Applied Physics Letters, 2012, 100: 024105.
[15] Xia Hui, Liu Guoqiang, He Wenjing. A New Imaging Logging Technology Based on Magnetoacoustic Tomography with Magnetic Induction [J]. Advanced Materials Research, 2012, 63: 433-440.
[16] Aliroteh MS, Scottt G. Arbabian A. Frequency-modulated magneto-acoustic detection and imaging [J]. Electronics Letters, 2014, 50(11): 790-792.
[17] Zhang Shunqi, Zhou Xiaoqing, Ma Ren, et al. A study on locating the sonic source of sinusoidal magneto-acoustic signals using a vector method[J]. Bio-Medical Materials and Engineering, 2015, 26: S1177-S1184.
[18] Nannapaneni N. 工程电磁学基础[M]. 北京:机械工业出版社, 2006: 35-37.
[19] Di S. Trust region method for conic model to solve unconstrained optimization[J]. Optimization Methods and Software, 1996: 237-263.
[20] Powell MJD. A new algorithm for unconstrained optimisation[M]. New York: Academic Press, 1970: 31-66.
[21] 高晋占. 微弱信号检测[M]. 北京:清华大学出版社, 2004: 154-166.
[22] 张顺起, 周晓青, 殷涛, 等. 基于连续波的频域磁声耦合成像方法正问题研究[J].生物医学工程研究, 2015, 34 (1): 1-6.
Preliminary Study on Inverse Problem of Magneto-Acoustic Imaging in Frequency Domain
Zhang Shunqi Ma Ren Zhou Xiaoqing Yin Tao Liu Zhipeng#*
(InstituteofBiomedicalEngineering,ChineseAcademyofMedicalSciences&PekingUnionMedicalCollege,Tianjin300192,China)
A preiliminary study on inverse problem of magneto-acoustic imaging was conducted in this paper to lay the foundation for magneto-acoustic imaging based on measuring method in frequency domain. Basing on the amplitude and phase characteristics of sonic source with different amplitude and distribution, the mathematical model and the reconstruction using vector method was investigated. Equations to vectors of different frequencies were set up. Optimization algorithm for nonlinear equations was used to solve the sound source location. Amplitude and phase characteristics with different source distributions and the reconstruction to the two sonic sources were simulated. The experiment on copper wire was performed to validate the vector theory and the reconstruction method. The summed amplitude and the phase were the vector summation of the points all over the sample. The sonic source distribution could be reconstructed, and the imaging resolution is less than 1 mm. The reconstructed error was less than ±0.4 mm. The reconstructed study on magneto-acoustic imaging method provided the fundamental to the study to complex tissue and the biomedical samples. It is significant to the magneto-acoustic imaging with a high resolution.
magneto-acoustic imaging; frequency domain; vector method; inverse problem; reconstruction.
10.3969/j.issn.0258-8021. 2016. 05.006
2016-01-08, 录用日期:2016-06-06
国家自然科学基金 (81171424);国家自然科学基金青年项目(61501523);天津应用基础与前沿技术青年项目(13JCQNJC14000)
R318
A
0258-8021(2016) 05-0548-07
# 中国生物医学工程学会高级会员(Senior member, Chinese Society of Biomedical Engineering)
*通信作者(Corresponding author), E-mail: lzpeng67@163.com

