基于CFD的左心室流场数值模拟研究现状与趋势

阿都建华 尹立雪 谢盛华

1(成都信息工程大学软件工程学院，成都 610225)2(四川省医学科学院·四川省人民医院心血管超声及心功能科超声心脏电生理学与生物力学四川省重点实验室，成都 610072)

基于CFD的左心室流场数值模拟研究现状与趋势

阿都建华1,2尹立雪2*谢盛华2

1(成都信息工程大学软件工程学院，成都 610225)2(四川省医学科学院·四川省人民医院心血管超声及心功能科超声心脏电生理学与生物力学四川省重点实验室，成都 610072)

随着计算技术的快速发展，计算流体力学在心脏血流流场模拟中得到广泛应用，取得了有价值的相关成果，在心脏功能的研究中扮演着越来越重要的角色。目前，运用计算流体力学实现心脏流体动力学特性及其流场数值模拟分析，已成为心血管基础和临床研究领域的一个重要研究方向，对心血管系统疾病预防、临床诊断和治疗具有重要意义。简述基于CFD的左心室流场数值模拟方法的发展过程、研究现状和方法分类，分析基于CFD的左心室流场数值模拟计算存在的主要问题，提出该研究领域未来的发展方向。

计算流体力学；左心室流场；数值模拟；流固耦合；

引言

心脏病学本质上是一门关于流的科学，心血管系统的主要功能是力学驱动、控制和维持整个人体系统中各个组织器官的血流灌注[1]。心室内的血液流场更为复杂多变，心动周期内不同时相血液流场主要表现为动态连续变化的层流和涡流，但在每个心动周期特定时相的流体总体特征通常又保持一定的相对稳定性和可重复性，特定时间点的血流涡流参数、血流速度分布、压力分布等流体特征量具有一定的不变性。不同的心脏病理解剖和病理生理异常，均会产生不同的异常血流流场。为了检测心脏疾病导致的血流流场异常，掌握心脏内血流变化过程及其时空分布就显得非常重要[2]。

近年来，研究人员已将先进的医学测量技术与计算机仿真技术、计算流体力学紧密结合起来，用于研究人体心脏的血液动力学状态，通过计算机数值计算和图像显示的方法，在时间和空间上定量描述流场的数值解。常规心脏血流动力学实验研究不仅风险高、花费大，而且也仅能获取速度、压力等有限的流动参数数据，而速度矢量、流线、壁面剪切应力等复杂的流场参数数据是不可能得到的。数值计算仿真技术成本低、效率高，不仅能有针对性地研究各种心脏几何变形、力学及流固耦合因素对血流动力学的影响，而且可以完成常规实验无法实现的生物力学多参数时空描述和可视化表达。当在体或离体实验研究不可行时，数值仿真就成为唯一可行的血流动力学观测手段。虽然仅仅依靠血流动力学的数值计算结果，还不能完全解释心血管疾病相关的病理生理机制，观测结果需要与临床医学实验结果相结合，但是这些计算结果将弥补实验研究的不足，有助于更好地揭示心血管疾病发生、发展的病理生理和病理解剖原因，从而可以对此类疾病的预防和治疗提供有价值的参考信息[3]。各种心脏疾病往往会在心动周期的全部或某些特定时相呈现出心腔内血液流场上的异常变化，因此深入研究心脏血液流场特征有可能为各种心血管疾病的早期精确诊断提供重要线索和依据。医学临床研究也已经证实，精确的心脏血流流场及其血流动力学信息(如血流速度、剪切率、剪切应力等)对于心力衰竭、心肌病、动脉粥样硬化、中风等众多心血管疾病的早期预警和诊断具有重要意义，同时也能为心脏外科手术的风险评估、手术时机指导及术后治疗提供重要的参考信息[4-9]。目前，运用计算流体力学实现心脏的流体动力学特性及其流场数值模拟分析已成为心血管研究领域的一个重要研究方向，基于CFD的左心室血流流场数值模拟研究在心脏功能的研究中扮演着越来越重要的角色，将在心脏功能状态的评价及预测、治疗决策、治疗方案优化、手术辅助等方面发挥重要作用。

1 基于CFD的左心室流场数值模拟分析方法类型

在已有研究中，心脏流场数值模拟方法的研究大多都以左心室内流场的变化为研究对象，基于CFD的左心室流场数值模拟方法大致可以分为3种[10]：规定几何结构法[11-23]、虚构流固耦合法(fluid structure interaction，FSI)[24-29]、真实流固耦合法[30-33]。这三种方法都具有良好的研究价值和临床应用价值，其中真实FSI方法具有更为广阔的应用前景，但同时也最为复杂。

1.1 规定几何结构法

规定几何结构法通常利用临床采集的图像进行几何结构建模，以此模型作为规定几何结构构建移动网格，并以心脏内壁为边界，将心脏内壁的移动作为边界条件，同时不考虑心脏的几何结构对血流产生的反馈作用力，最后进行心室流场的数值模拟。

图1 流场模式和左心室充盈期的等压线[23]Fig.1 Flow patterns and isobars in the LV during filling[23]

Vierendeels等以二维对称几何结构对左心室舒张期的血流流场进行建模，通过任意拉格朗日欧拉公式求解移动网格，实现流场域的模拟[23]。在心脏等容扩张开始后，开始进行模拟计算。在心脏的等容扩张阶段，假定血流流体在心室内部是静止的，并且速度为零，不存在压力差。在这个阶段，所有节点的压力都将根据心室壁模型内的杨氏模量变化进行计算。当心室压力下降到低于心房压力时，二尖瓣膜就会打开，此时心室内压力由心室壁的舒张和血流的流体动力学共同决定。在研究中，作为边界条件的二尖瓣血流模式以及二尖瓣打开时的心房压力都来自集中参数模型的独立计算。模拟结果如图1所示，分别展示了左心室充盈期4次时间步长的速度矢量和等压线，分别是充盈早期速度峰值(E峰)、舒张期后期、心房收缩期速度峰值(A峰)和A峰减速期。其中，第一个早期充盈E峰由心室舒张产生，第二个峰值是心房压缩产生的A峰，从图中可以充分观察到充盈期4个阶段的漩涡形成过程和压力分布。

Saber等基于CFD方法利用MRI数据实现左心室血流的数值模拟，通过采集一个心动周期内的MRI数据建立一个3D时变心脏内膜图像模型,再使用CFD方法模拟左心室的流场[17]。在建模过程中，使用了CMRTOOLS工具实现纵轴和横轴MRI切面的手工图像描绘处理；在血流流体的模拟过程中，则使用有限体积法进行计算。该模型的模拟结果展示了三维左心室内壁的收缩和舒张过程，并能很好地模拟流场的涡流等主要特征。心室血流流场结果都基本与活体临床实验一致。由于没有考虑瓣膜的影响，其流场速度模拟的准确性有一定局限性，图2展示了该模型模拟的横切面速度矢量分布，其中1～4是收缩期阶段速度矢量分布，5～6是舒张期阶段速度矢量分布。

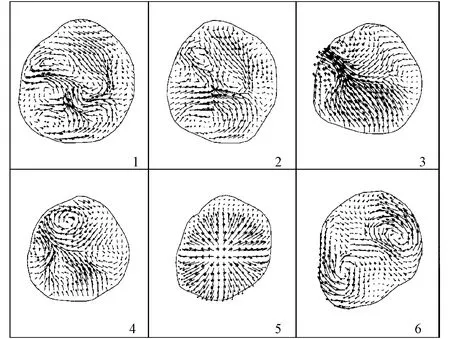
图2 横切面速度向量分布[17]Fig.2 Velocity in short-axis plane[17]

2003年，Saber等又完善了以前的研究内容，不但改善了纵向和横向切面图像的分割方法，而且在CFD模型中增加了近端左心房和升主动脉[18]。由于MRI无法提供瓣膜的清晰信息，因此研究中仅对二尖瓣和主动脉瓣做了近似模拟，无法对瓣膜口的精确位置、瓣膜的具体形态等细节问题做更为准确的建模和模拟，图3为该模型在4个舒张期阶段的横切面速度矢量分布，能明显看出形成了一个主要的大型前漩涡和一个后部小漩涡。

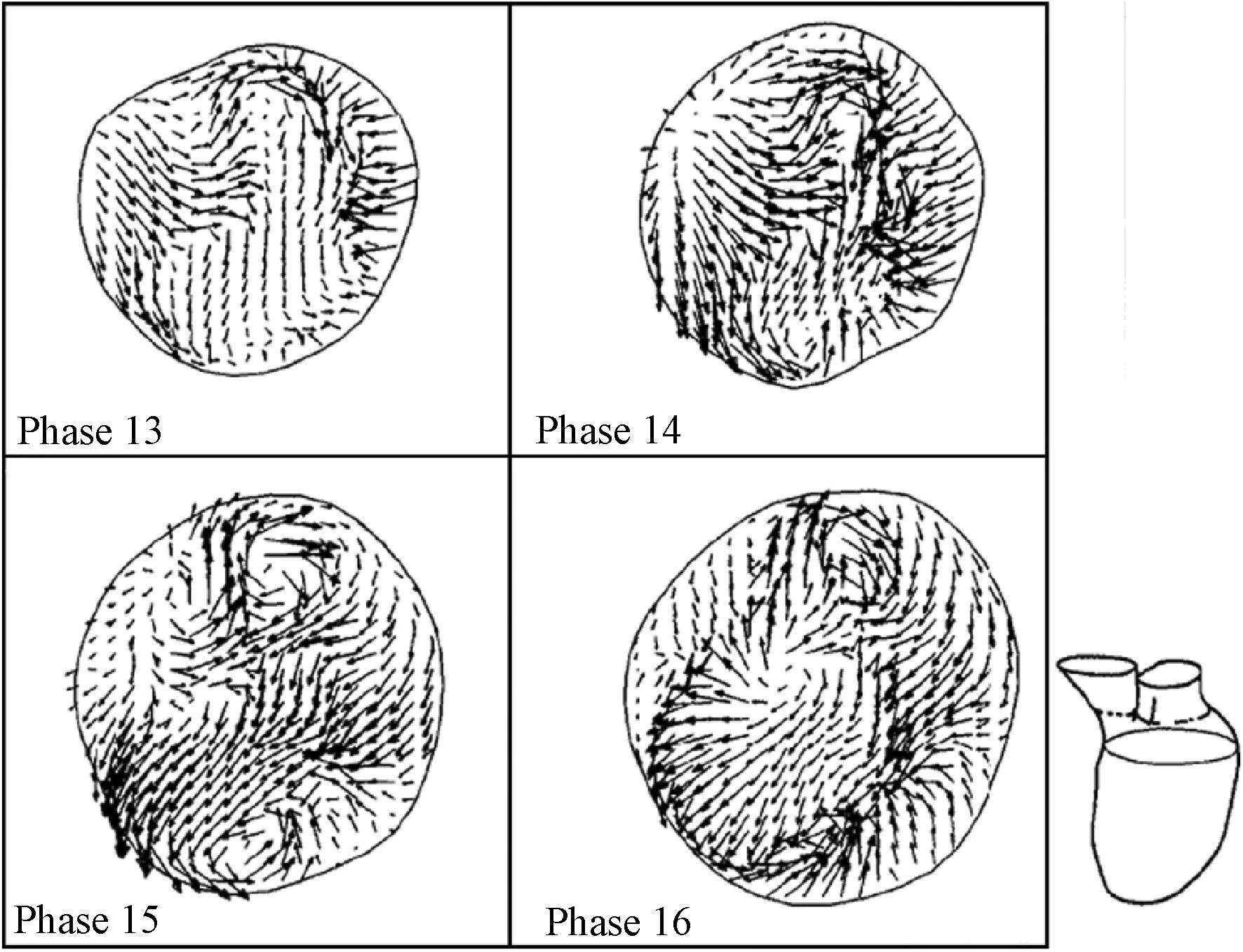
图3 横切面速度向量分布[18]Fig.3 Vectors of simulated diastolic velocities in a short axis plane[18]

Domenichini等建立了一个三维左心室模型，对舒张期的血流流体动力学进行研究[34]。该三维左心室模型是一个长椭圆形，流体动力来源于简化的波形输入血流，物理和数学模型如图4所示。该模型的流动方程采用贴体坐标系，并在方位角方向用傅里叶函数展开，最终方程使用混合有限谱差分技术进行数值化求解。在研究中，为了理解心室扩展期的主要血流变化现象，通过变化控制参数来实现血流动力学的分析。模拟结果显示，具有典型涡流结构特征的血流流场在控制参数发生变化时大致保持一致，直到用较低的斯特鲁哈尔数，血流流场才变化为弱湍流的形式。图5中展示了在特定常量参数时涡流随着时间的变化在一个对称平面中的演变过程，其中的(a)～(c)分别为3个不同时间步长时的y平面涡流矢量分布。

图4 物理和数学模型轮廓[34]Fig.4 Sketch of the physical problem and of the mathematical model[34]

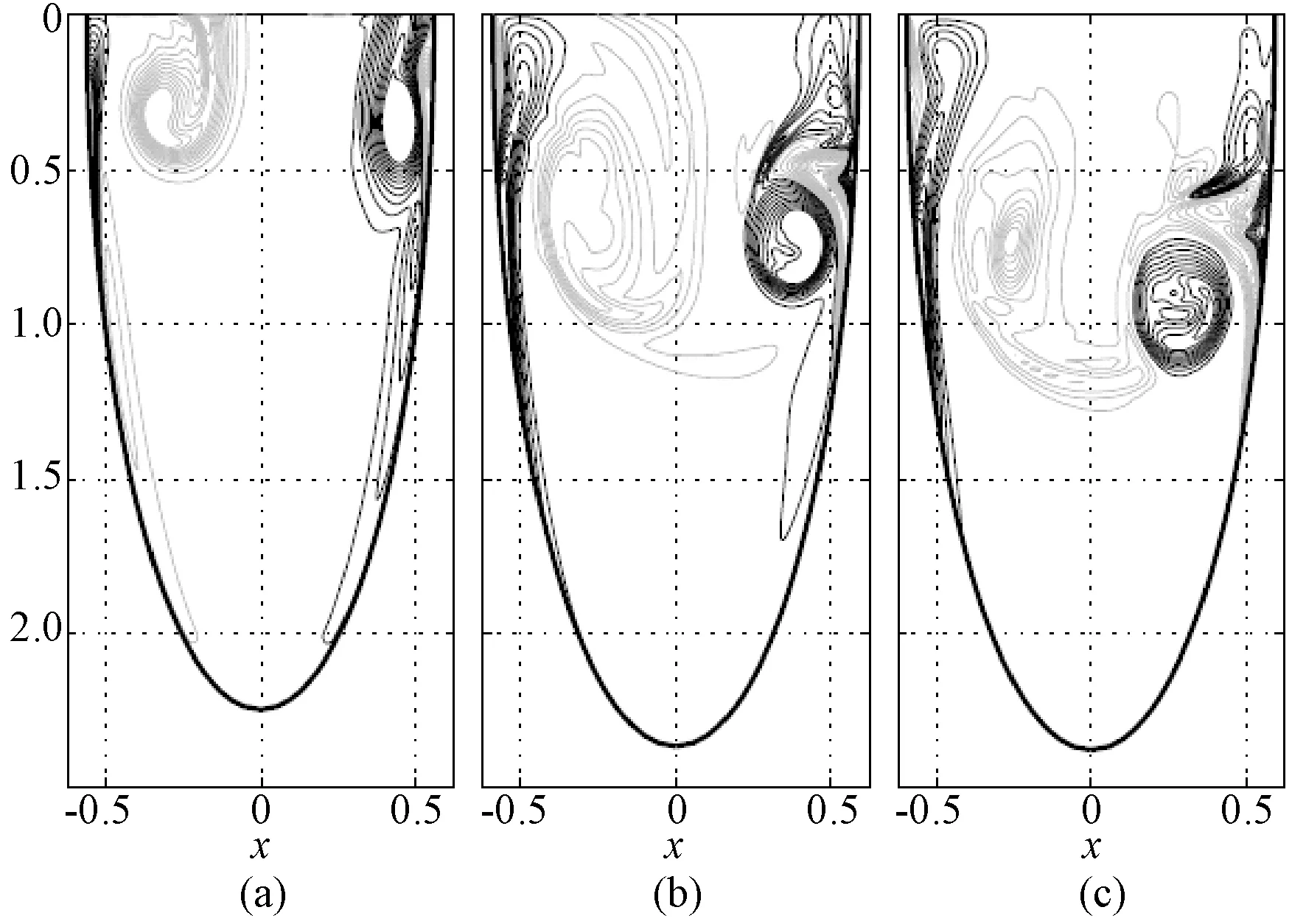
图5 对称平面的wy分布[34](涡流矢量的y分量, 斯特鲁哈尔数=0.072，斯托克斯数=144，ε=0.125)。(a) t=20/128, (b) t=10/128,(c)t=50/128Fig.5 Distribution of wy[34] (y component of vorticity vector) on the symmetry plane, Strouhal number=0.072, Stokes number=144, ε=0.125). (a) t=20/128, (b) t=10/128,(c)t=50/128

TORSTEN SCHENKEL等提出的方法[22]和Saber等的方法[17-18]类似，但其建立了更为准确的瓣膜模型。该方法使用了Karlsruhe心脏模型，并按标准的临床MRI图像采集流程采集数据，通过一个二维时变注入孔口描述心脏瓣膜，同时根据采集的纵轴图像估计瓣膜的位置和大小。模型中通过一个半自动的网格生成器创建计算网格，使用实现了任意拉格朗日欧拉公式求解的纳维-斯托克斯(Navier-Stokes)解算器完成计算过程。由于核磁共振扫描的时间分辨率无法满足CFD计算的需要，因此模型中采用了一个三阶贝赛尔曲线近似方案来实现平滑的边界和网格移动。模拟结果显示，在心脏舒张期间，通过二尖瓣的血流形成一个不对称的喷射，导致初始涡环不对称发展。这些流场特征不仅和活体实验结果完全一致，而且对注入血流边界条件及心房几何形状有极高的敏感性，如图6所示。其中，A部分表示速度概况、矢量及流量的测量，B部分表示曲线状心房时用不同彩色线条描绘的血流流线速度，C部分是直线状心房时用不同彩色线条描绘的血流流线速度。

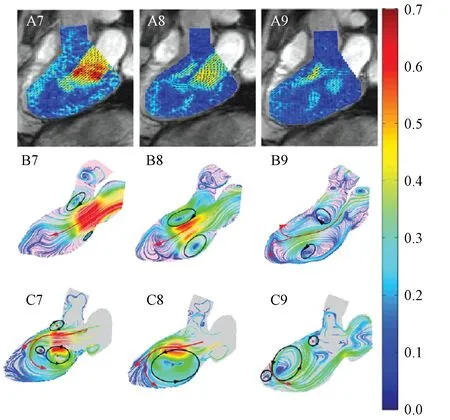
图6 注入条件变化血流模拟比较[22]Fig.6 Sensitivity to inflow conditions[22]

SIMON J. SONNTAG等将计算流体力学模拟研究方法和实验研究方法结合起来，量化研究心脏二尖瓣回流的影响[35]。该研究开发了一套模拟左心室的循环流动腔室实验研究系统，系统中采用3个不同的孔口模拟二尖瓣回流的变化，并同时利用二维多普勒超声和PIV测量记录流场域。同时，采用与实验系统完全相同的几何结构和边界条件利用CFD进行模拟。PIV实验结果和CFD计算模拟结果展现了高度的一致性，模拟的CDI也表现出与彩色多普勒图像一样的特性。在该研究中，数值模拟方法结果成功验证了实验研究方法的结果，并展示了实验方法和计算模拟方法相结合带来的灵活性。研究中使用的CFD模型如图7所示，基于圆孔和矩形孔的时均PIV和CFD的模拟结果比较如图8所示。

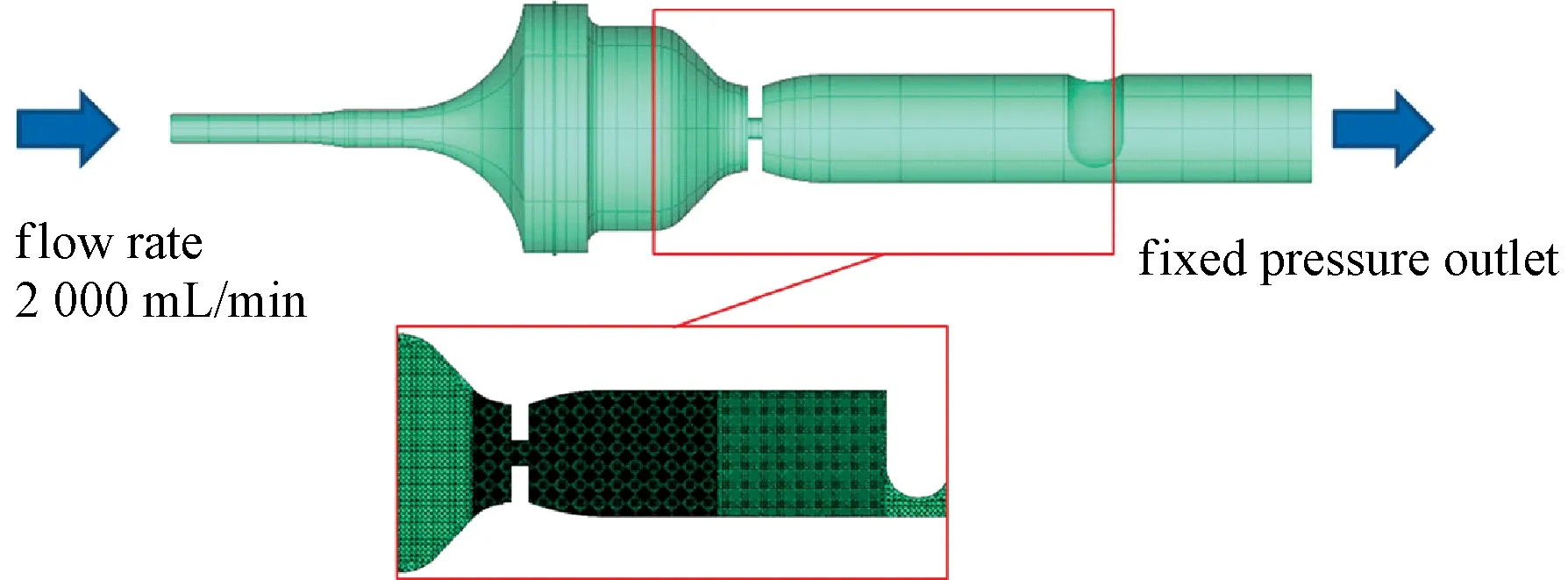
图7 CFD的CAD模型、边界条件和使用网格[35]Fig.7 CAD model, boundary conditions and used mesh (shown in one plane) of the CFD simulation[35]

图8 基于圆孔和矩形孔的时均PIV和CFD的模拟结果比较[35]Fig.8 Comparison of time-averaged PIV and CFD for the circular orifice[35]

1.2 虚构FSI方法

虚构FSI法是一种模拟心脏血流流场的宏观近似方法，利用浸入边界法适用于模拟形状复杂的弹性结构边界的特点，用浸入边界法将心脏结构简化为一个弹性纤维体，并利用插值狄拉克函数来描述血流和心肌组织之间的相互作用。

图9 模拟计算结果。(a)早期心室充盈阶段；(b)心室射血阶段；(c)通过二尖瓣膜的涡流运动；(d)右心室大涡流[27]Fig.9 Results from a computation.(a) A time early in ventricular filling, (b) A time during ventricular ejection, (c) Shows the vortex motion behind the mitral valve leaflets, (d) Shows a large vortex in the right ventricle[27]

浸入边界模拟方法不仅能计算流体的运动，而且还能同时计算沉浸在流体之中又和流体发生相互作用的弹性边界的运动[27]。在浸入边界法中，血流被看做是牛顿液体，并通过欧拉速度表示，压力分布在一个规则的三维计算格子中，血液动力则通过Navier-Stokes方程计算。在模拟计算过程中，不断地进行求解计算并替换由外力导致变形的弹性边界。弹性结构所描述的边界在计算网格空间中能连续自由移动，可以通过狄拉克函数计算这个过程，同时这种移动变形产生的力量会通过弹性边界传递给周边的相邻计算格子，这就表现为流体在外界动力的作用下运动，此时再次应用数值化狄拉克函数计算新的计算格子速度，然后通过计算格子的移动速度又来确定新的移动边界，最后将边界移动到新的位置。随着这些计算过程的迭代执行，新的网格边界位置随每个时间步长不断重新定位，流体则表现为不断的运动。

四大工程:给长城贴瓷砖、给赤道镶金边、给太平洋装栏杆、给喜马拉雅山安电梯间;四小工程:给苍蝇戴手套、给蚊子戴口罩、给蟑螂戴避孕套、给老鼠戴脚镣。

在文献[27]中，仅要求提供血流流体的物理属性、边界的弹性属性和边界的初始几何结构。在已经建立的模型基础上，采用GL(Graphics Library,GL)库开发了一个可视化的自定义展示系统，并在SGI(Silicon Graphics,SGI)工作站上运行，用以显示模拟计算的效果，如图9所示。在这个系统中，通过计算流体标记的运动来表示心脏内的血流运动，同时系统的控制管理非常灵活，可以自由控制计算过程，比如打开或关闭心脏模型中的任意一组纤维，并能随意改变观察的视角和放大兴趣区域。

雷诺数是表征方程中迁移惯性项与黏性项比值大小的量，在它的不同范围含有完全不同的两种流动——层流和湍流。Lemmon等开发了一个薄壁心室计算模型，结合生理雷诺数模拟血流和心肌组织交互过程，该模型能有效减少使用的计算资源，使模拟心室运动的数值计算可以脱离超级计算机，在普通的用户工作站上运行[24]。为了反映流体动力以及组织病理生理学上的变化，模拟过程中心肌组织和血流的相互作用使用浸入边界法计算，并通过压力耦合方程的半隐式方法来求解流体质量和动量守恒方程。在该模型中，并没有包含一个实际的二尖瓣膜来模拟控制孔口的开闭，而是在二尖瓣膜的孔口位置直接假设一个阀门进行模拟。该研究将计算模拟结果和临床数据进行了比较，显示出二尖瓣流线、心室流场和心房流场均与临床数据一致，心房流场的变化也和相关理论一致。此外，模型对心房和心室内压力场的跟踪也显示出了和活体测量一样的结果。由此可以看出，该模型能检查出由于心脏病变引起的舒张功能变化。

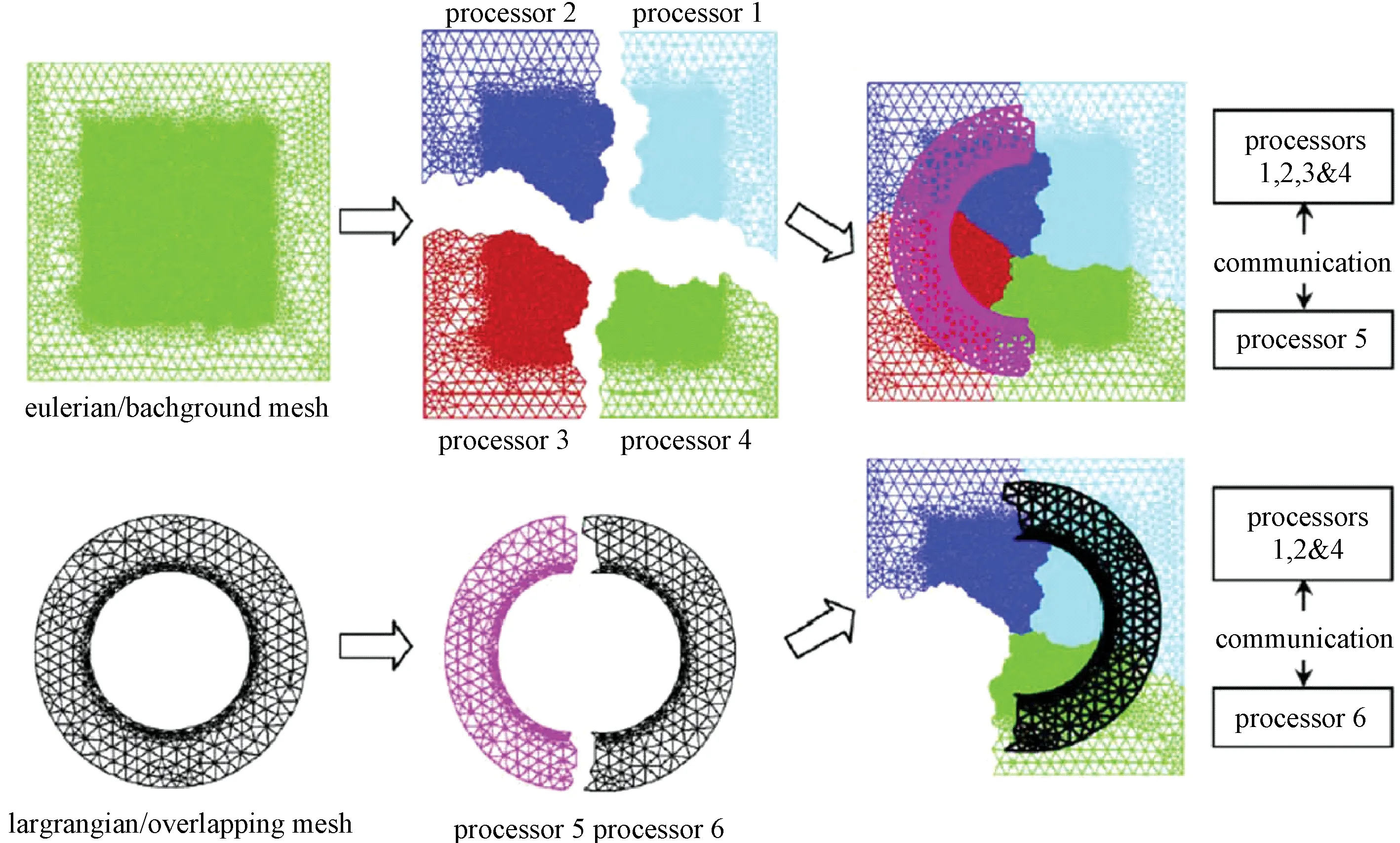
图10 网格分区以及背景与重叠网格之间的通信[37]Fig.10 Mesh partitions and communications between background and OGs[37]

Lemmon等针对心脏舒张功能已减弱的病例进行建模[25]，研究中应用的3个舒张期功能障碍的研究病例和临床观察的舒张期流场变化一致。研究结果表明，心脏舒张延迟会减少心脏早期的充盈量，如果心室的僵硬程度不断加强，充盈量就会持续减少。同时，在心房收缩期增强心房压缩力度会导致更高的后期充盈速度和心房压力。该研究结果显示，心脏功能障碍状态可以通过改变心肌纤维静止状态的长度和僵硬度的关联关系来建模，这大大增强了研究人员未来对心脏疾病建模的信心。

由于血流和心肌组织的物质差异太大，瓣膜的数据信息又难以采集，致使生理条件下瓣膜运动的数值分析难度很大，因此在心脏数值建模中，主动脉瓣膜位置的流固耦合常常都被忽略。2003年，Hart等研究了心脏收缩过程中主动脉瓣膜位置的流固耦合效应[36]。拉格朗日乘子虚拟域方法作为一种数值模拟方法，常被用以描述计算流体领域的大瓣膜运动。在研究中，将该方法应用于一个主动脉瓣膜支架的三维有限元模型，然后为模型提供瓣膜及流经血流的机械行为数据。模拟计算结果显示，在心脏收缩期间，植入支架的瓣膜按流体运动方式随血流移动。

2007年，Tai等提出了浸入对象法，实现包含流固耦合的三维非定常流模拟[37]，该方法中联合应用了一个自由矩阵隐式双时间步长和有限体积法的并行非结构多网格Navier-Stokes解算器，使用流固耦合方法来详细研究三维非定常流的流动变化，并基于此研究人工心脏瓣膜的打开过程。在浸入对象方法在动量守恒方程的人工压缩子循环的过程中，引入了一个表示人体动力能量的F来获取速度分布。在流场域中，浸入了对象网格来定义对象的边界，背景位置和重叠网格的通信处理过程如图10所示。该方法的优点是几乎任意形状都可以加入模型而无需重构网格，因为重构网格将消耗大量的时间和计算资源。这样就能在生理条件下，利用人工心脏瓣膜完成复杂详细的非定常血流和血流瓣膜流固耦合的三维模拟。实验结果已经验证，这种并行隐式非结构多网格方法在计算三维非常定流的过程中具有高效性和精确性的特点。

1.3 真实FSI方法

真实FSI法分别利用有限元方法和计算流体力学方法对心脏系统的组织结构和血流进行建模，再通过流固耦合算法描述组织结构和血流之间的相互作用。一个成功的真实FSI心脏血流模拟方法最少需要合理地解决以下3个方面的问题。首先，表示心脏几何结构的解算机必须能描述非线性、各向异性和不均匀的心脏壁组织结构特征；其次，CFD代码必须能处理流场域的大变形，并且同时更新相应的计算网格；再次，流固耦合算法必须能确保固体结构和血流的正确耦合。因此，真实FSI方法的描述方法最为复杂，需要集成心肌力学、非线性有限元、计算流体力学、计算网格动力学、流固耦合算法来实现心脏流场的模拟。当前，这些方法的研究已经取得了重要的进展，Fung等[38]、Lin等[39]提出了心脏壁肌肉结构的本购方程，Hunter等[40]、Smith NP等[41]提出了分析心室力学的有限元模型，Navier-Stokes方程的任意拉格朗日欧拉公式已经成功地在计算流体力学移动网格和FSI中得到了应用[42-43]，Zhang Hou等[44]提出了同步交互的流固耦合算法。

Hunter等结合心室解剖、心肌组织的几何结构和材料属性，细胞膜离子通道，钙调控和心脏肌细胞的肌丝力学来解释心脏的集成功能，建立了分析心室力学的有限元模型[40]。他们在模型中专门设计了计算框架，用来建立心脏细胞和组织的结构及功能与整个心脏整体集成功能运转之间的复杂关联联系。然而，如果希望该模型能够洞察理解更多的心脏疾病过程，则还需要包含更多的生理功能，包括代谢和信号转导通路。

Watanabe等将亚细胞分子和心脏器官生理水平关联起来，开发了一个基于有限元的三维模拟程序[45]。该模拟程序结合了兴奋收缩偶联及其应用的细胞学机制，模拟包含人类左心室收缩功能的流固耦合。该模型在细胞元模型中采用了描述横桥动力学的神经元模型和四态模型，用有限元网格对心腔内的心室墙和血流进行建模，应用任意拉格朗日-欧拉公式求解自动网格的更新，并采用了强耦合策略。在模型中，还使用电子模拟肺循环，左心房作为前负荷，弹性腔模型作为后负荷，模拟心室充盈的动力和喷射过程，如图11所示。他们成功模拟再现早期快速充盈和心房压缩的双相填充流过程，近似于临床的观测结果。因此，该模拟器中的流固耦合模型能分析出充盈流的波传播速度，同时对于在宏观层面上建立分子异常和临床疾病之间的联系是一个有力的分析工具。

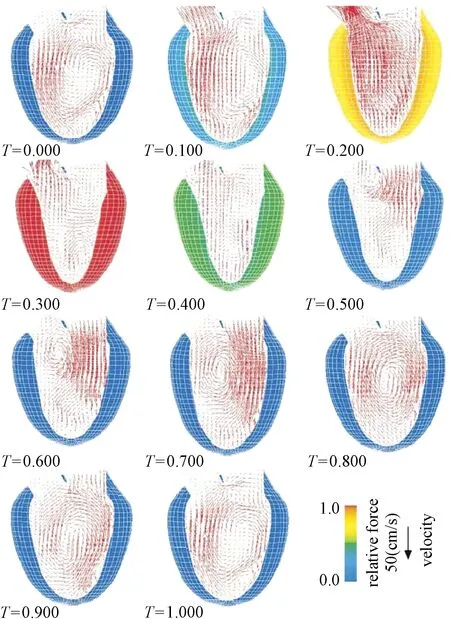
图11 左心室收缩和心室内血流的时延图像[45]Fig.11 Time-lapse images of LV contraction and intraventricular blood flow[45]

程永光等为了验证在左心室充盈过程中基于流固耦合架构的商业软件的可行性，研究了心脏充盈阶段的流固耦合模拟过程，显示出其在心脏功能研究和临床应用领域的巨大前景[10]。他们使用实现了任意拉格朗日-欧拉公式求解的商业软件ADINA来模拟左心室的流场，具体解决方案是采用Navier-Stokes方程的任意拉格朗日-欧拉公式求解流体问题，采用有限元模型对心肌组织进行建模求解，并在每个时间步长里同时求解耦合方程。对于人类心脏的左心室充盈流，采用基于规定时变杨氏膜量的三维椭圆薄壁模型几何结构来进行模拟，如图12所示。虽然充盈过程中结构变形很大，但耦合能平稳收敛。

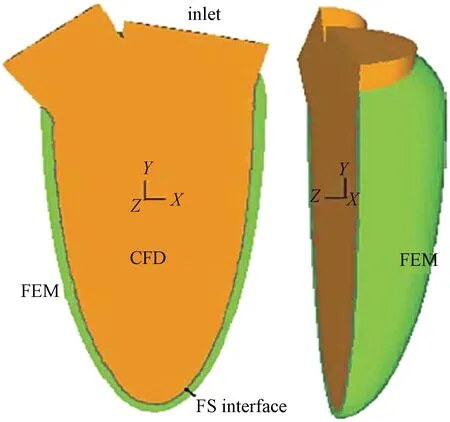
图12 用于流固耦合模拟的心室模型几何结构。绿色表示心室薄壁，橙色表示流场、入口和二尖瓣口[10]Fig.12 Geometry of the model ventricle for the coupled simulation. ventricular thin wall; flow domain andin let, mitral orifice[10]

程永光等详细分析了心室模型的压力容积关系、压力的空间时间分布、瞬态速度向量和涡流模式，认为分析结果和实际测量数据从定性和定量角度都一致。在图12中，可以观察到不同时间步长下的速度模式。在快速充盈阶段，会产生一个强力喷射，将血流从二尖瓣喷射到心室腔内。在这个强力喷射的驱动下，在二尖瓣口下方的区域会形成一个环流。随着快速充盈的继续，这个涡环平稳地向心室中部移动。作为一个附加结果，在减速期会在主动脉流出口处形成一个小的涡环。随后，在心脏舒张后期，涡环会到达膨胀的心室中部，同时涡环的前端向后移动，而后端仍然向前移动。同时，逐渐减弱的涡流开始扩大并移出通道，进而在心室舒张后期被输入流摧毁。充盈阶段几个典型时刻的速度向量如图13所示。

图13 充盈阶段几个典型时刻的速度向量[10]Fig.13 Velocity vectors at several typical moments during the filling[10]

研究者对该模型的模拟过程做了许多简化假设，如薄壁心室几何结构、各向异性和同质材料，忽略二尖瓣以及统一输入流速度，都明显限制了模拟模型的实际临床应用。但是，研究工作验证了这个框架的结构变形耦合能力，为未来建立真实心脏充盈过程模型提供了有力的参考。

Sebastian等建立了一种心脏血流流场模拟的三维代码耦合方法[33]。在该方法中，他们首次用心肌复合模型替换了原来规定几何运动的Karlsruhe心脏模型，并且分别利用有限体积法和有限元法，实现任意拉格朗日-欧拉公式和固体力学有限元弹性方程的离散化，同时通过数据交换迭代策略，保证底层基础控制方程的接口平稳。在该模型使用的代码耦合框架中，分别应用Abaqus 6.7-1(www.simulia.com)以及Fluent6.3.26 (www.fluent.com) 作为FEM和FVM的解算器，接口交互通信使用由弗劳恩霍夫研究所(www.scai.fraunhofer.de)开发的网格并行代码耦合接口MpCCI 3.0.5 (www.mpcci.de)来实现，最后通过迭代计算完成心脏流场的模拟。图14展示的是该研究模拟不同时间段的心室内流场。

图14 KaHMo FSI/MRT中不同时间段的心室内流场[33](左上：充盈早期；右上：充盈后期；左下：心房收缩；右下：中期喷射)Fig.14 Inner-ventricular flow field in KaHMo FSI/MRT for different time-frames[33](Top left: early filling; top right: late filling;bottom left: atrium contraction; bottom right: mid ejection)

2 存在的问题及发展趋势

综上所述，基于CFD的左心室流场数值模拟研究工作已经取得了巨大的进步，但仍然存在许多问题。

首先，基于采集图像的建模方法大多都使用MRI数据来对左心室的形态和运动进行建模，MRI不仅检测费用较高，而且通常临床常规检查所获取数据的时间分辨率非常低(9～17帧/s)。超声心动图有更高的时间分辨率，在扇形B模式条件下通常可以达到100～200帧/s，在实验环境下甚至可以达到2 000帧/s，可以有效克服这个问题。此外，由于强磁场的原因,MRI对诸如体内有磁金属或起搏器的特殊患者不适用。因此，需要进一步研究基于超声心动图的左心室建模方法。另一个问题是如何通过实验数据实现三维几何结构的自动生成。通常，采集的图像数据是二维切面图，通过在这些图像上插值来实现三维几何结构的重建。当前，这个过程大多在计算机辅助设计软件上手工完成或半自动生成，这将消耗大量的时间。建立自动化分析方法可以节省时间，排除或最小化人机交互过程产生的主观性。最后，需要在通过成像数据重构三维几何结构的过程中量化复杂的变化过程，比如心动周期内心室的运动变化、成像过程中主体的运动以及成像体位位置的不确定，将来都需要进一步量化从而支持临床决策。

总之，左心室数值模拟研究未来的发展方向将集中在以下几个方面：

1)临床图像数据时间分辨率的提高。当前，核磁共振扫描图像的空间分辨率较高，但时间分辨率非常低，需要采集多个心动周期的图像才能实现左心室数值模拟建模，在此过程中容易遗漏一些细节信息。未来可以继续通过提高磁共振成像设备的扫描速度来提高图像的时间分辨率，但短期内还难以实现。此外，可以结合计算机图形图像技术，充分利用超声心动图高时间分辨率的优点，实现对左心室的数值模拟建模。

2)左心室流场流固耦合新方法的研究。虽然已有许多左心室流场数值模拟研究充分考虑了流固耦合因素，并对此做了深入研究，做出了较好的模拟结果，但这些研究在计算效率和模拟准确度上都需要进一步提升，因此建立一套在心肌力学上简化但在血流流场上模拟效果好、计算效率高的左心室流固耦合计算模式非常重要。

3)左心室二尖瓣膜的精确模拟。由于现有的成像设备和图像技术通常难以准确提取二尖瓣膜的位置和移动数据信息，现在的研究大多通过数据假设来完成二尖瓣膜的数值模拟。随着科技的进一步发展，通过对各种成像设备图像信息的研究，可以结合图像处理技术来提取真实的二尖瓣膜数据信息，以实现更为准确的左心室流场模拟。

4)心脏扭曲运动的模拟。心脏的扭曲运动是导致升主动脉内旋动流的主要原因，也是影响左心室内部血流流场变化的重要因素，但目前的数值模拟研究基本都还未考虑到这一因素对流场变化的影响。

5)三维心室几何模型的自动生成。计算图像分割技术已经日趋成熟，可以研究适合超声图像的图像分割算法，自动分割一个心动周期内的超声图像，实现自动构造三维心室几何模型。

6)量化三维心室几何模型重建过程中复杂变化产生的影响。在三维几何模型重建过程中会产生各种复杂的细微变化，这些变化会造成心室内模拟流场的变化，并最终影响模拟流场的准确性。这些复杂的细微变化可以通过反复实验来确定，并建立模型量化其影响，通过建立参数调整模型来最小化这些变化产生的影响。

7)三维心脏流场数值模拟模型中临床病人数据的注入配置方案。支持临床应用是三维心脏流场数值模拟的主要目的，便捷高效地注入配置临床病人数据，准确再现一个心动周期内病人的三维心脏流场变化过程，从而满足临床诊断和治疗的需要。

[1] Richter Y, Edelman ER. Cardiology is flow[J]. Circulation, 2006, 113(23):2679-2682.

[2] Carlhäll CJ, Bolger A. Passing strange flow in the failing ventricle[J]. Circulation: Heart Failure, 2010, 3(2):326-331.

[3] 刘有军, 刁越, 高松. 血流动力学与动脉粥样硬化 (一)[J]. 北京生物医学工程, 2004, 23(4):293-295.

[4] Foster GE, Deng Z, Boulet LM et al. Changes in left ventricular function and coronary blood flow velocity during isocapnic hypoxia: A cardiac magnetic resonance imaging study[J]. Journal of Cardiovascular Magnetic Resonance, 2016, 18(S1)： 1-2

[5] Zhu Y, Qian M, Niu L et al. Two-dimensional measurement of blood flow velocity in rat arteries based on ultrasonic particle image velocimetry[J]. Journal of Southern Medical University, 2014, 34(9):1305-1309.

[6] Zhou F, Cui YY, Wu LL et al. Analysis of flow field in mechanical aortic bileaflet heart valves using finite volume method[J]. Journal of Medical & Biological Engineering, 2016, 36(1): 110-120

[7] Shang EK, Nathan DP, Sprinkle SR et al. Peak wall stress predicts expansion rate in descending thoracic aortic aneurysms[J]. Annals of Thoracic Surgery, 2013, 95(2):593-598.

[8] Altnji HE, Bou-Saïd B, Berre WL. Morphological and stent design risk factors to prevent migration phenomena for a thoracic aneurysm: A numerical analysis[J]. Medical Engineering & Physics, 2014, 37(1):23-33.

[9] 隋成龙. 左心室舒张早期功能模型评价方法研究[D]. 西安：西南交通大学， 2013.

[10] Cheng Y, Oertel H, Schenkel T. Fluid-structure coupled CFD simulation of the left ventricular flow during filling phase[J]. Annals of Biomedical Engineering, 2005, 33(5):567-576.

[11] Baccani B, Domenichini F, Pedrizzetti G. Vortex dynamics in a model left ventricle during filling[J]. European Journal of Mechanics-B/Fluids, 2002, 21(5):527-543.

[12] Baccani B, Domenichini F, Pedrizzetti G. Model and influence of mitral valve opening during the left ventricular filling[J]. Journal of Biomechanics, 2003, 36(3):355-361.

[13] Baccani B, Domenichini F, Pedrizzetti G et al. Fluid dynamics of the left ventricular filling in dilated cardiomyopathy[J]. Journal of Biomechanics, 2002, 35(5):665-671.

[14] Long Q, Merrifield R, Yang G et al. The influence of inflow boundary conditions on intra left ventricle flow predictions[J]. Journal of Biomechanical Engineering, 2003, 125(6):922-927.

[15] Nakamura M, Wada S, Mikami T et al. A Computational Fluid Mechanical Study on the Effects of Opening and Closing of the Mitral Orifice on a Transmitral Flow Velocity Profile and an Early Diastolic Intraventricular Flow[J]. JSME International Journal Series C Mechanical Systems, Machine Elements and Manufacturing, 2002, 45(4):913-922.

[16] Nakamura M, Wada S, Mikami T et al. Computational study on the evolution of an intraventricular vortical flow during early diastole for the interpretation of color M-mode Doppler echocardiograms[J]. Biomechanics and Modeling in Mechanobiology, 2003, 2(2):59-72.

[17] Saber NR, Gosman A, Wood NB et al. Computational flow modeling of the left ventricle based on in vivo MRI data: initial experience[J]. Annals of Biomedical Engineering, 2001, 29(4):275-283.

[18] Saber NR, Wood NB, Gosman A et al. Progress towards patient-specific computational flow modeling of the left heart via combination of magnetic resonance imaging with computational fluid dynamics[J]. Annals of Biomedical Engineering, 2003, 31(1):42-52.

[19] Schoephoerster RT, Silva CL, Ray G. Evaluation of left ventricular function based on simulated systolic flow dynamics computed from regional wall motion[J]. Journal of Biomechanics, 1994, 27(2):125-136.

[20] Taylor TW, Okino H, Yamaguchi T. Three-dimensional analysis of left ventricular ejection using computational fluid dynamics[J]. Journal of Biomechanical Engineering, 1994, 116(1):127-130.

[21] Long Q, Merrifield R, Xu X et al. Subject-specific computational simulation of left ventricular flow based on magnetic resonance imaging[J]. Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine, 2008, 222(4):475-485.

[22] Schenkel T, Malve M, Reik M et al. MRI-based CFD analysis of flow in a human left ventricle: methodology and application to a healthy heart[J]. Annals of Biomedical Engineering, 2009, 37(3):503-515.

[23] Vierendeels J, Riemslagh K, Dick E et al. Computer simulation of intraventricular flow and pressure gradients during diastole[J]. Journal of Biomechanical Engineering, 2000, 122(6):667-674.

[24] Lemmon JD, Yoganathan AP. Three-dimensional computational model of left heart diastolic function with fluid-structure interaction[J]. Journal of Biomechanical Engineering, 2000, 122(2):109-117.

[25] Lemmon JD, Yoganathan AP. Computational modeling of left heart diastolic function: examination of ventricular dysfunction[J]. Journal of Biomechanical Engineering, 2000, 122(4):297-303.

[26] McQueen D, Peskin C. Shared-memory parallel vector implementation of the immersed boundary method for the computation of blood flow in the beating mammalian heart[J]. The Journal of Supercomputing, 1997, 11(3):213-236.

[27] McQueen DM, Peskin CS. A three-dimensional computer model of the human heart for studying cardiac fluid dynamics[J]. ACM SIGGRAPH Computer Graphics, 2000, 34(1):56-60.

[28] Peskin CS. Fluid dynamics of the heart and its valves[C]//Proceedings of APS meeting. New York: American Physical Society, 1997: 2.

[29] Vesier CC, Lemmon Jr JD, Levine RA et al. A three-dimensional computational model of a thin-walled left ventricle. In: Proceedings of the 1992 ACM/IEEE conference on Supercomputing, 1992: IEEE Computer Society Press, 1992: 73-82.

[30] Chahboune B, Crolet J. Numerical simulation of the blood-wall interaction in the human left ventricle[J]. The European Physical Journal Applied Physics, 1998, 2(3):291-297.

[31] Vierendeels J, Riemslagh K, Dick E, et al. Computer simulation of left ventricular filling flow: impact study on echocardiograms[J]. Computers in Cardiology, 1999, 26: 177-180.

[32] Watanabe H, Hisada T, Sugiura S et al. Computer simulation of blood flow, left ventricular wall motion and their interrelationship by fluid-structure interaction finite element method[J]. JSME International Journal Series C, 2002, 45(4):1003-1012.

[33] Krittian S, Janoske U, Oertel H, et al. Partitioned fluid-solid coupling for cardiovascular blood flow[J]. Annals of Biomedical Engineering, 2010, 38(4):1426-1441.

[34] Domenichini F, Pedrizzetti G, Baccani B. Three-dimensional filling flow into a model left ventricle[J]. Journal of Fluid Mechanics, 2005, 539:179-198.

[35] Sonntag SJ, Li W, Becker M et al. Combined computational and experimental approach to improve the assessment of mitral regurgitation by echocardiography[J]. Annals of Biomedical Engineering, 2014, 42(5):971-985.

[36] De Hart J, Peters G, Schreurs P et al. A three-dimensional computational analysis of fluid-structure interaction in the aortic valve[J]. Journal of Biomechanics, 2003, 36(1):103-112.

[37] Tai C, Liew K, Zhao Y. Numerical simulation of 3D fluid-structure interaction flow using an immersed object method with overlapping grids[J]. Computers & Structures, 2007, 85(11):749-762.

[38] Fung YC. Biomechanics: circulation[M]. Berlin: Springer Science & Business Media, 2013.

[39] Lin D, Yin F. A multiaxial constitutive law for mammalian left ventricular myocardium in steady-state barium contracture or tetanus[J]. Journal of Biomechanical Engineering, 1998, 120(4):504-517.

[40] Hunter PJ, Pullan AJ, Smaill BH. Modeling total heart function[J]. Annual Review of Biomedical Engineering, 2003, 5(1):147-177.

[41] Smith N, Nickerson D, Crampin E, et al. Computational mechanics of the heart. from tissue structure to ventricular function[J]. J Elasticity, 2000, 61(1):113-141.

[42] Souli M, Ouahsine A, Lewin L. ALE formulation for fluid-structure interaction problems[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 190(5):659-675.

[43] Zhang Q, Hisada T. Analysis of fluid-structure interaction problems with structural buckling and large domain changes by ALE finite element method[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190(48):6341-6357.

[44] Zhang H, Bathe KJ. Direct and iterative computing of fluid flows fully coupled with structures[C]//First MIT Conference on Computational Fluid and Solid Mechanics. Boston: MIT, 2001: 1440-1443.

[45] Watanabe H, Sugiura S, Kafuku H, et al. Multiphysics simulation of left ventricular filling dynamics using fluid-structure interaction finite element method[J]. Biophysical Journal, 2004, 87(3):2074-2085.

The Recent Advances and Prospects on the Numerical Simulation of Flow Field within Left Ventricular Based on CFD Techniques

Adu Jianhua1,2Yin Lixue2*Xie Shenghua2

1(ChengduUniversityofInformationTechnology,Chengdu610225,China)2(SichuanAcademyofMedicalSciences&SichuanProvincialPeople′sHospital,SichuanProvincialKeyLaboratoryofUltrasoundinCardiacElectrophysiologyandofBiomechanics,Chengdu610072,China)

With the rapid development of computer technology, computational fluid dynamics has been widely used in the numerical simulation of flow field in heart and some valuable relevant outcomes has been obtained. CFD is playing an increasingly important role in the study of cardiac function. Currently, it has become an important research in basic and clinical cardiovascular research areas in which CFD is used to simulate and analyze fluid dynamics and flow field in heart, which is important for prevention, diagnosis and treatment of the cardiovascular disease. In this paper, we describe the development of numerical simulation of flow field within left ventricular based on CFD, the research status and classification method. We summarize the main issues of numerical simulation of flow field within left ventricular based on CFD and put forward the future direction of this research field.

computational fluid dynamics; flow field within left ventricular; numerical simulation; fluid-structure coupling

10.3969/j.issn.0258-8021. 2016. 05.011

2016-02-22， 录用日期:2016-04-14

国家自然科学基金(30970698);四川省图形图像智能系统协同创新中心开放基金;成都信息工程大学引进人才项目(KYTZ201322)

R318

A

0258-8021(2016) 05-0587-011

*通信作者(Corresponding author)， E-mail: yinlixue@yahoo.com