整体兼容 运动联系
——“梯形的认识”教学实践
□张伟明
整体兼容 运动联系
——“梯形的认识”教学实践
□张伟明
图形与几何是小学数学领域中不可或缺的重要组成部分。本文以新教材的“梯形的认识”一课展开教学实践,由浅入深,前有蕴伏把脉认知规律,中有突破厚实探究活动,后有发展渗透思想为主要策略。在信息技术环境下,以丰富学材、层次反馈、多元运动来促进学生空间观念的形成。
图形与几何 信息技术 空间观念
图形与几何是小学数学领域中不可缺少的重要组成部分。《义务教育数学课程标准(2011年版)》在该领域目标中,要求学生经历图形的抽象、分类、性质探讨、运动、位置确定等过程,掌握图形与几何的基础知识和基本技能;要求学生建立空间观念,初步形成几何直观。具体到图形的认识,重要的是对图形本质特征的把握,以及在认识图形的过程中发展学生的数学思考,提升数学空间观念。从过去只重视简单的几何知识的传授、偏重于计算,到现在着眼于学生空间观念的培养和生成,提升了几何教学的层次。
面对这一领域的变化,如何更科学地实施教学,真正达到新课标所提出的要求?围绕图形与几何这一专题笔者进行了深入的学习和研究,对图形与几何的有效教学策略有了一定的认识,本文选取了人教修订版小学数学四年级上册第66页“梯形的认识”这一教学内容谈一些体会。
一、课前蕴伏很重要
在此之前,学生已经了解了四边形的一些特征,知道什么是平行,什么是垂直,认识了平行四边形。对梯形的形状、特征也有了初步的了解。但他们对什么是梯形,梯形的各部分名称是什么,梯形与其他四边形的关系是怎样的并不了解。
在了解了学生的认知基础后,教师从学生的实际情况出发,在设计时,首先整体呈现的是可供学生操作的材料。在提炼出梯形后,开展的各项活动让学生对梯形的认识从模糊到清晰,使学生真正掌握其意义,并对四边形各图形之间的关系有一个整体的认识。
二、课上活动要到位
(一)丰富的学材,给学生创造思考的空间
本课从引入为学生提供的长方形和梯形学具,到普米软件带来的互动生成的及时反馈,到为学生精心准备的交互运动的swf软件,再到只提供梯形一条边来画梯形这样的习题设计,这是教师对教材从内容、结构、呈现方式等多个角度作出的理性重建。而给予学生的学材,则是希望能为学生创设思考的空间,激发他们内在的数学学习潜能,引导他们自主探索。让学生在经历知识的发生发展过程中,感悟知识的本来面目,从而使学生学会运用数学的思维方式去观察、分析现实世界,去解决实际问题,实现各方面能力的发展。
(二)层次的反馈,让学生实现意义的建构
【片段一】辨一辨
师:在下面这些图形里有梯形吗?说说你的理由。
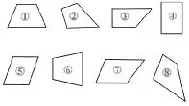
师:②号为什么不是梯形?
生:没有平行线。
师:⑤号呢?有平行线,为什么也不是?
生:⑤号有两组对边平行是平行四边形。而梯形只能有一组对边平行。
师:⑧号为什么是梯形呢?
生:有且只有一组对边平行。
师:这里有你熟悉的梯形吗?谁能来介绍一下?
生:直角梯形,有两个角是直角。
生:等腰梯形,两条腰相等。或有对称轴。
师:那这些梯形的高你们会画吗?
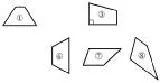
【片段二】画一画
在方格纸中,以DC为一条边画出梯形。

学生根据要求画好梯形后,教师进行反馈。
师:你怎么知道这些同学画的都是梯形呢?
生:只有一组对边平行的四边形是梯形。
师:我们来看,这位同学跟老师画的有什么不同?
生:高不同,底也不同。
生:直角梯形。
生:高相同但是形状不同。
师小结:同学们画的梯形可真丰富!老师还发现有的同学画的梯形,高虽然是相同的,但他们能画出这样的斜梯形,或这样的直角梯形,或是等腰梯形。还能画多少个这样的梯形?要怎么画?
生:能画无数个梯形,只要平移AB就好。
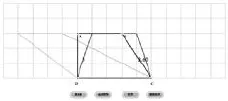
显示高 自动变换 记录删除记录
【片段三】折一折
给学生提供一个平行四边形纸片,教师的问题是这样的:
师:你能只折一次让它变成两个直角梯形吗?你们是怎么折的?
师:提高难度,你能想办法折出两个完全相同的梯形吗?
师:你能想到更多不同的折法吗?怎么折?有多少种折法?
通过层层递进的问题式反馈,帮助学生清晰地掌握了梯形的特点,辩证地找到了不同的梯形的本质属性,直观地体现了梯形和平行四边形的关系。整个教学过程一气呵成,而通过观察、类比、运动联系等方式,则能够让学生的思维在不断地碰撞中前行,从而有效地提高学生思维的敏捷性、深刻性,构建完整的知识体系,进而实现其意义建构。
(三)多元的运动,帮助学生拓宽思维的宽度
本课在设计上,关注了知识的形成和联系,希望学生能在运动中加深对知识的理解,在运动中体会图形的一种联系,从而培养学生的空间意识。课上,第一次运动是在学生已经操作了教师提供的学件,重叠得到多样图形,并通过观察发现其中有一类四边形比较有特点的时候,教师不失时机,利用白板软件的交互性这一特性,旋转三角形(如图1),并涂色拖出梯形,这样的旋转带来的好处是平行线的位置不会改变,但得到的是多样的梯形,丰富了学生头脑里的梯形表象。第二次运动是同一件学材的另一种旋转,当学生已经辨析了梯形,对梯形有了比较多的认识,这时候的变式和突破就势在必行了。于是,笔者把这件学材换了一种旋转方式,旋转长方形(如图2),此时的旋转改变的是图形的平行线的位置,这样学生会更专注于变式的梯形。通过旋转,通过观察,梯形的本质属性自然而然就在师生的追问中,越来越清晰了,那就是只有一组对边平行的四边形才能叫梯形。
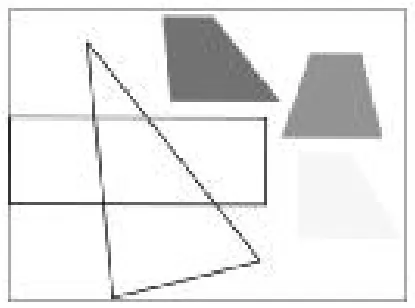
图1
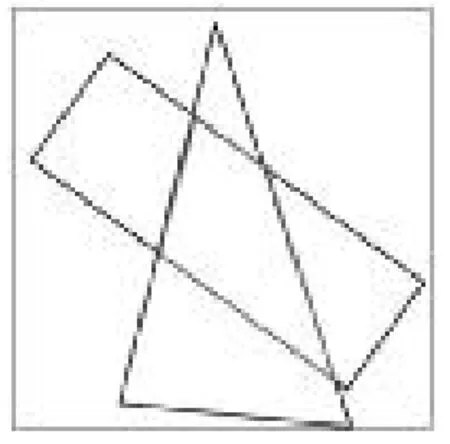
图2
第三次运动是学生在以CD为边画了一个梯形之后,教师在反馈学生作品时发现,有的同学画的高相等但形状不同,于是就很自然地进行引导,还能画出不同的梯形吗,能画多少个,这样就自然过渡到了梯形的等积变形中来。在辨析的过程中,学生头脑里关于梯形的认识越来越丰厚,图形间的运动互化也有了一点感受。此时,教师再把折平行四边形抛出,沟通平行四边形和三角形、梯形、平行四边形的互化关系,随着学生思维的步步呈现,教师让折痕再次运动起来,升华了课题。
(四)立体的建构,帮助学生完善知识结构
本课在构建上,试图改变以往教学中对知识网络建构的不足,用联系、运动的观点,立体建构起学生的知识体系,因而在课程设置上力争把学生作为学习的主人,为学生创设了和谐、民主的学习氛围。从而营造师生、生生之间的多向交流,使学生发展了自己的数学思想的同时,学会进行数学交流,倾听别人的想法,并且注重学生对四边形的建构,使其厘清关系,形成系统、完整的认识。
整节课,在学习和认识图形的过程中,学生找到了同上下底梯形的变与不变。在平行四边形中寻找梯形,在动态、联系的过程中,学生感受到了图形间的相互联系。总结、沟通四边形关系的过程也是一样,学生在这个过程中,构建了联系的观点,厚实了认知的结构。
三、后续渗透不可少
在平移中感受到了同底等高的梯形有无数个,在感受这些图形的过程中,渗透了平面图形等积变形的数学思想,也渗透了跟梯形面积相关的一些因素,对后续梯形面积的学习有较大的帮助。当折平行四边形时,把平行四边形折成两个完全相同的三角形、梯形、平行四边形,渗透面积推导方法。在旋转折痕的过程中,还能感受到梯形可以和三角形、平行四边形互化。当梯形的上底逐渐变小乃至为0时,梯形变成了三角形,当三角形的“上底”逐渐变大乃至和下底相等时,三角形就变成了梯形直至平行四边形,渗透面积转化思想方法,蕴含梯形面积计算方法的“万能”。
总之,在图形与几何领域的教学中,教师应当做到前有蕴伏,中有突破,后有发展,在过程中渗透思想方法,设计丰富有效的活动,给学生提供探究空间的同时,将观察、操作、思考、推理、表达融为一体。让学生带着整体的思想、运动的眼光、联系的观点来认识图形,构建图形知识的网络体系。从而享受学习成功的喜悦,发展空间观念。
[1]李娟玲.浅谈形象思维能力的培养[J].江苏教育,1999(04).
[2]刘胜俊.小学数学课堂教学艺术[J].课堂内外(教师版),2012(11).
[3]杨庆余.小学数学课程与教学[M].北京:高等教育出版社,2004.
[4]王春锋.梯形的认识教学实践与反思[J].小学数学教育,2014(10).
(浙江省杭州市胜蓝实验小学 310000)

