教学智慧生成的“四个要点”
□濮志坚
教学智慧生成的“四个要点”
□濮志坚
教学智慧是教师面临复杂教学情况所表现的一种敏感、迅速、准确的判断能力。要成为一名优秀的数学教师,可着力从教学智慧生成的“四个要点”——精读教材、精准预设、精研学情、精心倾听等方面积淀专业素养,磨炼教学智慧,适时抓住课堂资源,动态生成精彩课堂。这样,教师才能在“意外”出现时或特定情境中沉着“接招”,瞬间决策,让课堂在随机推进中留住鲜活,朝着“明亮一方”高速“冲刺”!
教学智慧 四个要点 教材 预设 学情 倾听
当我们走进新课程导引下极富开放性、生成性的新课堂时,教师面临着严峻的挑战:在教案的预设思路中,你能随机应变去吸纳现场生成的精彩吗?在把握教材、凭借文本的同时,你能机敏应对节外生枝的干扰吗?在平等对话的课堂交往中,你能挥洒自如地正确引导吗?所有这些场面的应对,恐怕都涉及教师的一项非常重要的专业素养——教学智慧。教学智慧是教师面临复杂教学情况所表现的一种敏感、迅速、准确的判断能力。如果教师没有深厚的教学功底,没有高超的应变术,是难以让课堂教学“善始善终”的,必定会因各种意外而让教学“打折扣”。然而,教师在课堂上出现的不知所措的状况,真的只是教学智慧的缺失吗?若深究一下,笔者认为是综合素质的欠缺与不足。
那么,教师应该着力从哪些方面积淀专业素养,培养教学智慧,从而铸造精彩课堂呢?
一、精读教材——教学智慧的“基点”
记得一位知名特级教师曾说过:“教材研究透了,课实际上也就备得差不多了。”这话虽然听起来似乎有些玄乎,但实际上相当有道理。精读教材是上好一节课的核心环节。教师在备课之前,应精心解读教材,准确而全面地把握教材内容,唯此方能设计出完善而周密的教学方案。反之,如果教师自己对教学内容都没有把握到位,那么就很难设计出高质量的教学方案。在这种情况下,“走教案”都勉为其难,要是一旦遇上课堂中随时都可能出现的意外,又谈何灵光一闪的“教学智慧”呢?以下是人教版二年级上册“解决问题”的一个教学片段。
【教学片段】
师:我们先来帮面包房师傅解决问题。我一共做了54个面包。第一小队买了22个面包,第二小队买了8个面包。还剩多少个面包?
师:你能解决这个问题吗?以小组为单位,相互讨论一下。(小组合作)
生:54-22-8=24。
师:你是先算什么,再算什么?
生:我先算54-22=32,再算32-8=24。(教师随即板书:54-22=32 32-8=24)
师:先算54-22,你是怎么想的?
生:因为我先算第一小队买走了22个面包,所以先算54-22。
师:说得真好,我们把54-22=32、32-8=24叫作分步列式,把54-22-8=24叫作综合算式。不管是分步还是综合,其实方法是一样的。我们把它们叫作方法一。
【分析】
显然,当学生回答“54-22怎么想”的时候,教师没有抓住教学资源,没有顺着学生的思路走下去,而是继续走教学流程。那么,在许多教师看来,是该教师教学智慧的缺失,但是否也看到了,该教师是否知道解决问题该教给孩子什么?是否研读教材了?在教学“解决问题”有关的课时,许多教师会比较注重计算结果,只要学生能列出算式,就“鸣金收兵”。殊不知,学生是知其然,却不知其所以然。
那么,就“解决问题”这个内容而言,教师该如何把握教程呢?笔者认为,首先该关注“数量关系”渗透。许多学生对两种数量采用何种运算非常头痛,通过对信息的充分理解,数量关系的分析(总数-第一队买走的个数=剩下的个数,剩下的个数-第二队买走的个数=剩下的个数),并进行运算方法的选择,才能熟练地掌握解决问题的技能,并将“数量关系”熟练灵活地应用于解决问题之中。另外,应该注重“中间问题”的寻找。分析完“54-22”的数量关系后,教师应接着追问:54-22可以求出什么?(第一小队买走22个后,还剩几个面包)再求出什么?解决问题时,学生知道了分析问题的方法,培养了寻找中间问题的能力,那么解决问题自然势如破竹了。对教材研究透了,教学也就有了强有力的支撑和“基点”。
二、精准预设——教学智慧的“起点”
一堂好课,不能没有好的教学预设。教学预设包含甚广,但笔者认为,当前数学教师需要着力关注的有两大方面:一是对教学语言的预设(如导入语、评价语等),二是对学情走向的预设(如学生可能出现的各种反应或即兴回答等)。大多数教师比较注重前者,很少在后者下功夫。细节决定成败,如果不注重后者,不预设学生在课堂上可能出现的各种声音,那就有可能让教师不知所措,甚至不知所云,让听课老师瞠目结舌。这是人教版小学数学三年级上册“四边形的认识”的教学片段。
【教学片段】
师:在长方形里面画一条线段,能否分成两个四边形。(学生操作)
生:我是横着画,竖着画的,画了两种。
师:还有别的画法吗?
生:我是斜着画的。
师:只有这么三种吗?
生:还有很多种,只要别沿着两个斜对的角画就行了。
师:那会变成什么?
生:会变成两个三角形。
师:你们可真棒。(接着教师课件出示图形)这样可以吗?变成什么了?

图1
生:变成了一个正方形和一个长方形。
师:嗯?左边的是正方形吗?
生:是的。
师:确定吗?
生:确定。
师只好无奈地说:你们说是什么就是什么吧!我们接着往下看。
【分析】
对于三年级的学生来说,仅凭借肉眼,是很难分辨左边的图形是长方形还是正方形。而教师此时表现的无奈,可以说明其没有充分估计到学生可能会有的各种想法,也就是预设不足、不到位。分析一下学生出现错误判断的原因:图1中左边的图形,本身就与正方形相似,而且经过投影,或者因为学生座位的关系,当然有各种可能性发生。教师在课前,就应仔细观察自己预设的这个图形,分析学生有可能出现的各种状况,这样就不会不知所措了。
数学是一门非常严谨周密的学科,不能想当然。当学生无法判断时,教师应询问学生:我们怎么样可以知道这个图形是正方形呢?学生肯定回答:用尺子量一量,四条边都相等,就是正方形。教师就可以用尺子量,让学生知道这是错误判断。从中也可以教育学生,很多时候不能光用直觉判断,要用工具判断,要用事实说话。所以,许多时候出现的意外状况,不是教师教学智慧欠缺,而是预设得不够到位,只有精心预设教师的课堂语言和学生可能的回答,才能更好地行走于课堂,才能运用自己的教学智慧,展开精彩的瞬间。
三、精研学情——教学智慧的“支点”
在提倡有效教学的今天,在课前设计教案时,比较透彻地了解学生的情况显得尤为重要。当我们把特级教师的教学设计搬到自己的课堂当中时,难免会发现其实自己的学生并不是很“合作”,教师在参加上课比赛或上展示课时,都要经过反复的试教,也就是“磨课”,才能勉强通过。为什么名师的教学设计在自己的课堂中一下子行不通了,为什么精心设计的教案还要经过如此的反复试教才可以真正走上课堂呢?笔者认为其中一个重要的原因是我们设计教案时往往更注重教材,对学生却关注不够。这样就会造成设计出的教案不适用,教学效果不佳,对提高课堂效率起不到太大的作用。以下是人教版小学数学三年级下册“小数的初步认识”的教学片段。
师:我们知道1米等于10分米(板书:1米=10分米),老师把1米平均分成10份,取其中的一份是?
生:1分米。
师:1分米用分数表示就是——
生:十分之一米。
师:现在,谁知道分数十分之一米代表什么意思?
(教室里一片寂静)
师:十分之一米,表示把1米平均分成10份,取其中的一份,就是十分之一米。谁愿意来说一说?
生:把1米分成10份,取其中的1份,就是十分之一米。
师:你们发现他漏了哪个词?
生:平均分。
师:对啊,那谁能来说一说?
……
师:通过我们的共同研究,我们知道了1分米不但可以用分数十分之一米来表示,也可以用小数0.1米来表示,虽然它们表示的方法不同,但表达的意思却是一样的。现在,你知道小数0.1米表示什么意思呢?(又冷场了,师连忙补救)
师:0.1米的意思和十分之一米的意思是一样的,表示把1米平均分成10份,取其中的一份,就是0.1米。(这时生才反应过来)
课前,教师清晰地知道,小数的初步认识要以分数的知识为基础来学。但是,教师却没有了解学生的学情。因为“分数的初步认识”是三年级上册学的内容,到下一册学小数时,许多学生对分数的认知已经有些模糊,需要教师重新唤醒学生的旧知,才能更好地学习新知。在以上教学片段中,教师表现出来的种种不知所措,课堂中的种种冷场,很明显和学生对分数的认知有密切的关系。如果教师在课前了解了学生对分数的认知状况,先给予必要的复习回顾,有了这个桥梁,对学好新知必将是一个有力的“支点”。
四、精心倾听——教学智慧的“亮点”
在平时的课堂教学中,教师应善于倾听学生的发言,去捕捉教学过程中稍纵即逝的、极有利用价值的、动态生成的教学资源,及时调整教学进程,改变教学策略,提升课堂教学的时效性与针对性,将教学智慧发挥得淋漓尽致,从而增强教学效果,提高课堂效率。以下是人教版小学数学三年级下册“平均数”的教学片段。
【教学片段】
师:老师将班中一组男生(4人)和一组女生(5人)一次连续踢毽子的成绩绘制成了统计表。仔细观察,从表中你能发现哪些信息?
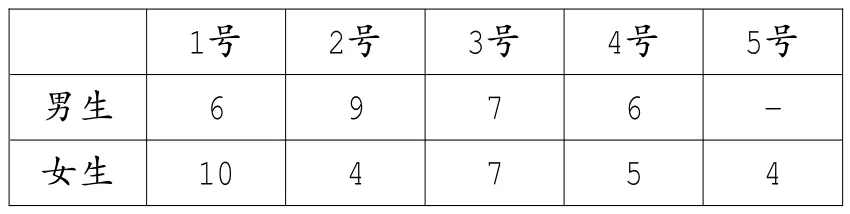
1号 2号 3号 4号 5号男生6 9 7 6 -女生 10 4 7 5 4
……
师:同学们发现了这么多信息,如果这是一次小组比赛,你们肯定想知道:胜利属于男生还是女生呢?
生:我认为是女生,因为女生1号踢了10个,踢得最多。
师:哦,你是这样想的。还有不同意见吗?
生:我认为女生赢,因为女生人数多,踢的总个数也多。
生:我认为是男生,因为男生踢的平均数多。
(教师有些不知所措,怎么这么快出现了平均数)
师:哦,你已经知道平均数了。
师:同意女生的举手(都举手了)。同意男生的举手(就刚刚回答的那个男生举手)。现在意见不统一,怎么办?这样吧,咱们来一次小小的辩论赛,大家可以发表自己的意见,也可以反驳别人的观点,看看谁说得最有道理。(学生讨论)
师:谁来说说你赞同谁的观点,为什么?
生:我认为女生获胜,因为女生的人数多,总数也多。
生:女生踢得最少是4个,男生最少是6个,所以男生获胜。
(学生想表达的,也是光比某个同学的成绩,但教师没有认真倾听)
师:哦,你是这样想的。
师小结:经过大家的讨论,有的同学提出了比某一个同学的成绩,如女生1号踢得最多,女生就获胜,光比某一个同学的成绩,你认为合理吗?(不合理)那么比两组同学踢的总个数,你认为公平吗?(不公平)为什么?
生:男生人数少,女生人数多。
师:那怎么样比才公平呢?我们再讨论一下。
【分析】
这一教学片段中,当教师问道:胜利属于男生还是女生时,显然,教师预设之中只需要学生回答男生获胜或者女生获胜就行了。之后,设计讨论和辩论环节,认为预设多么完美,教学过程将多么精彩。教师心中如此巧妙的设计,哪肯轻易删减。谁知,学生哪管老师你怎么预设的,在没有讨论和辩论之前,就把自己认为男生获胜或女生获胜的理由给说了,而且连这时不想让他提前出现的“平均数”都出来了,这可伤脑筋,怎么办呢?教师的做法是,当作没有听见,只听见孩子有不同的声音就行了,反正有些认为男生获胜,有些认为女生获胜,就可以继续自己的预设——先讨论,然后进行辩论赛。
学生的声音,你用心倾听了吗?前面三个学生的回答,多么精彩啊,你怎么能当作没有听见呢?设想,这个片段如果这样改:
生:我认为是女生,因为女生1号踢了10个,踢得最多。
师:哦,是啊,男生最多的才9个,也就是说,你认为只要比男生组和女生组踢得最多的那个同学就行了,是吗?
生:我认为女生赢,因为女生人数多,踢的总个数也多。
师:哦,你是用男生和女生人数来比较的,女生人数多,踢的总数自然就多,是这么推理的吗?
生:我认为是男生,因为男生踢的平均数多。
师表示出吃惊的样子:这位同学说了一个我们第一次接触的数——平均数,能说给大家听听吗?
师小结:刚刚经过讨论,同学们出现了3种情况,第一个同学说,比男生组和女生组踢得最多的那一个同学的成绩就行了,你们认为可行吗?
生:不可行,我们比的是两个组的成绩,光比一个同学不行。
师:那比他们两个组的踢的总个数行吗?公平吗?
生:不公平,因为两个组人数不一样,女生人数多。
师:那怎么比公平呢?
生:比平均数。
这个片段中,教师紧紧抓住这三个学生的信息:比最大数、比总个数、比平均数。根据学生的三种声音,教师通过追问,让他们分析哪种最为合理。如此教学,教师充分把握课堂自然生成的资源,发挥了教学智慧,不盲目实施自己的教案,及时改动教学进程,自然是智慧的课堂,高效的课堂。
总之,教师只有关注学生的需要,聆听课堂上所涌现的各种声音,倾听他们内心的想法,走进学生的心灵,在此基础上,教师才能逐渐磨炼出教学智慧,抓住课堂资源,动态生成精彩课堂,才能在“意外”出现时或特定情境中沉着“接招”,瞬间决策,让课堂在随机推进中留住鲜活,朝着“明亮一方”高速“冲刺”!
[1]陈果.关注精心预设,构建动态生成[J].小学教学(数学版),2010(5).
[2]苏志强.老师,请您倾听学生的声音[J].小学数学教育,2012(3).
(浙江省绍兴市柯桥区夏履镇中心小学 312000)

