关注命题设计 彰显过程评价
——以“简易方程”为例谈试卷命题设计
□杨明岚 柏凌
关注命题设计 彰显过程评价
——以“简易方程”为例谈试卷命题设计
□杨明岚 柏凌
要做好书面测验评价,首先要做好试卷命题工作。那么,如何用恰当的方式评价学生的“四基”达成情况?如何评价教师的教与学生的学?如何编制出一份高质量的测试卷呢?本文将从“关注四基,恰当评价学生理解和掌握情况”“关注现实,灵活运用知识解决实际问题”“关注读图,重视多元表征间的转化”“关注过程,挖掘知识背后的内涵”及“关注能力,重视数学素养的形成”等五个方面进行阐述。
命题 评价 思考
《义务教育数学课程标准(2011年版)》指出:“评价应以课程目标和内容标准为依据,体现数学课程的基本理念,全面评价学生在知识技能、数学思考、问题解决和情感态度等方面的表现。评价不仅要关注学生的学习结果,更要关注学生在学习过程中的发展和变化。”“根据评价的目的合理地设计试题的类型,有效地发挥各种类型题目的功能”以及“积极探索可以考查学生学习过程的试题”。所以,测试命题就不能仅关注知识技能,还要着眼于学生数学素养的评价,命题的设计要更多地尝试从落实数学思想、发挥试题对发展学生思维能力、提升学生数学素养方面的导向作用。那么如何用恰当的方式评价学生的“四基”达成情况?如何评价教师的教与学生的学?如何编制出一份高质量的测试卷呢?对此,笔者特以小学数学人教版(修订版)五年级上册第五单元“简易方程”为例,积极探索可以评价学生学习过程的命题。
一、关注“四基”,恰当评价学生理解和掌握情况
在设计命题时,如何做到关注“四基”,评价“四基”,走出记忆性、程序性的问题呢?对此,我们应淡化形式考查,突出对知识理解的评价。这类命题并不要求死记硬背数学概念,也不强调直接套用方法。事实上,大多数学生学习理解概念最好的途径是通过操作、图示或应用,把丰富的概念内涵、外延和思想方法蕴含在实际问题情境中。
【命题1】右图表示某小学有600个男生。
○=2△,则女生有( )人。
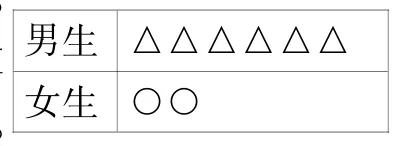
男生 △△△△△△女生 ○○
【分析与思考】本题重在了解学生的数学阅读能力。我们的数学教学不仅要帮助学生理解数学符号及其表达式的意义,还要让学生读懂文字、符号和表格所表达的问题含义。因此,本试题主要关注从数形结合、数值代入、符号等值代入等多角度考查学生对方程的解、解方程的概念的应用。让学生运用所学知识分析、转化等,灵活地解决问题。让学生在解决问题的过程中感悟数学的等价、转化、抽象等思想。
【命题2】下面哪幅图的天平所表达的关系,能用方程来表示?( )

【分析与思考】对概念的考查,笔者认为要关注将概念从文字表述转换成符号的、图像的等形式表征即可。此题,借助以天平为直观载体来理解方程的意义,便于学生以等式的性质为依据,从整体上理解方程的含义,有利于学生理解方程所揭示的等量关系,有助于感悟方程的实质、等价思想和建模思想。这样设计不仅把背概念直接填空改成了理解概念后选择填空,并且还评价检测了学生“动手操作”的应用情况和基本数学活动经验的积累情况。
二、关注“现实”,灵活运用知识解决实际问题
笔者认为评价学生的真实水平,就要重视挖掘学生身边的数学素材,不断创设新颖的现实问题情境,让学生在解决问题的过程中,用数学眼光审视问题,能从各类文字与图表中抽取所蕴含的数学信息,并利用个人有关的数学知识经验解决问题,从而发现问题背后的数学知识结构。同时,让数学化的现实问题成为学生独特见解或创新思维的催化剂,使学生在解题过程中也能认识数学学习的重要价值,从而增强学好数学的兴趣和信心。
【命题3】长兴到杭州的铁路全长约100千米,高铁列车以285千米/时的速度从长兴开往杭州。
(1)开出t小时后,高铁列车离长兴有( )千米(用含有字母的式子表示)。
(2)从下面三个数中选择一个数代表t(请将你选的数圈起来),那么第(1)小题的值是( )。
25小时 2.5小时 0.25小时
【分析与思考】对于本题主要考查学生用字母表示数量关系,即根据数量关系的陈述写出代数式,这是进一步学习代数的技能。在试题中体现让学生能够将语言文字的表述转换成直观符号表征,这既是提升学生抽象概括能力的过程,也是发展数学符号意识的过程。第(2)小题,随着t的值不断变化,距离发生变化,让学生体会变量间依存、对应的关系,这是函数思想的重要内涵,此外该小题重要考查学生在具体的情境中选择合适数的能力,如果将第(2)小题改为“如果t=0.25小时,那么高铁列车离长兴有( )千米”。那么“代入求值”的技能依然考查了,但“数感”考查的因素就被弱化了。
【命题4】科学分析表明:人体体重与自身血液重量存在一定关系。如果用m表示人体体重,用n表示人体血液重量,公式m÷n=13表示m与n之间的关系。王老师的体重是78千克,他体内血液的重量约是( )千克。
【命题5】下面是长兴浙北大厦的购物收据。
你能算出篮球的单价吗?请将该收据填写完整。

【分析与思考】这两题都是新的问题情境,学生依据“新问题”,要展开分析、推理,灵活地解决问题。“命题4”通过方程“m÷n=13”简洁地表达人体体重与血液重量间的关系,学生通过分析理解m、n及表达式的含义,从而代入求出n;“命题5”提供了真实的情境,让学生读懂由收据所表达的问题的数学含义,用数学眼光审视问题,能够从收据中抽取所蕴含的数学信息,分析解读信息,灵活地解决问题。
三、关注“读图”,重视多元表征间的转化
在教学中,我们发现学生的阅读审题能力很欠缺。因此,本试卷试题不但要从审读文字信息考查学生,还要考查学生读图表、符号和图形所蕴含的数学信息的能力,帮助学生借助图表理解数学符号、式子、方程的意义,进行多元表征的转化,培养学生理解和运用数学的能力。在本单元的试卷中多处可见用图示表征解决问题的试题。
【命题6】如右表,如何由x列中数得到y列中的数?( )
A.x列中的数都加3
B.x列中的数都减3
C.x列中的数都乘3再减1
D.x列中的数都乘2再加1
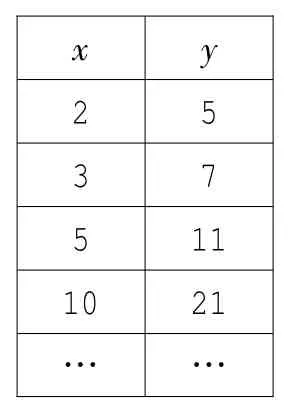
x y 2 5 3 7 5 11 10 21……
【命题7】读图,说说下面含有字母的式子表示的含义。
(1)4x表示( )。 (2)s-4x表示( )。
(3)4(x-y)表示( )。(4)4(x+y)表示( )。

【分析与思考】“命题6”和“命题7”主要考查学生的读图能力。借助图、表,让学生通过对图、表的观察分析,结合具体的情境,自己读取信息,选择信息,处理信息,解决问题,把图表表征转化成符号表征(代数式),再把符号表征转换成语言文字(意义)表征,在这样一个解决问题的过程中促进学生理解图表所蕴含的运算意义。
四、关注“过程”,挖掘知识背后的内涵
试卷中的试题不仅要关注学生学习内容的掌握情况,还要特别关注学习过程评价。因此,我们应充分了解学生的学习过程,让学生能提取已有活动经验去解决问题,挖掘知识与技能背后所隐含的数学知识,积极探索一些可以考查学生学习过程的试题。
【命题8】方程(32-4x)÷8=0的解与下列哪个方程的解相同?( )
A.4x=8 B.4x+8=32 C.32-4x=0 D.x=6
【分析与思考】传统的命题比较关注结果,或增加一些干扰因素让学生辨析、选择,很少评价学生的计算步骤或程序,及其理解程序和步骤的道理。而本题的设计目标,并不是最终看方程的解是多少,而是学生通过观察找到同解方程,考查学生对“方程的解”和“解方程”这两个知识点灵活运用的一个过程。
【命题9】一块三角形瓷砖面积是S,正好铺满如右图所示的地面。地面的面积是( )。
【分析与思考】本题不仅考查学生解决问题的观察、画图等分析能力,会用式子表示图形的面积,而且也考查学生的空间想象能力和利用图形、分析图形解决问题的能力,这也是积累数学活动经验的过程,是进一步学习第六单元多边形面积的基础。本题其实是一个转化、推理问题,可以展现不同学生用不同程度的知识、技能解决问题,对于高数学能力的学生可以运用转化推理思想解决;对于低数学能力的学生可以借助画一画、分一分等操作解决。
五、关注“能力”,重视数学素养的形成
数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想以及应用意识和创新意识,是小学数学学习的核心问题,也是衡量学生是否具有数学素养的重要标志。因此,本试卷的重点应放到考查学生运用观察、分析、表达等方法来解决问题的综合能力上。
【命题10】你能把下面的线段分成两段,使其中一段的长度是另一段的1.5倍吗?(写出必要的思考过程)

【分析与思考】好的命题,应为学生多策略解决问题提供空间,综合考查学生应用知识解决问题的能力。解决该题,方法1:用算术方法解答:12÷(1.5+ 1);方法2:用方程解答:x+1.5x=12。用方法1解决的这部分学生,可以评价检测出他们的逻辑能力强,当然也有部分学生是用画图、找关系、列出算式等方法解答的,体现了数形结合思想;用方法2解决的这部分学生具有代数思想,能把问题符号化来解决,体现了符号化思想。可见,不同的解决策略,可反映学生不同的思维能力。
【命题11】如右图。
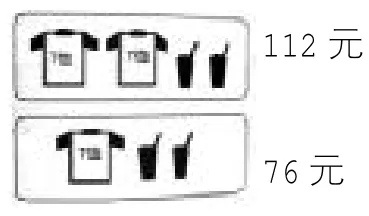
(1)求T恤的单价。
(2)求饮料的单价。
(写出你得出上述解答的过程)
【分析与思考】该题涉及的知识技能并不明确,没有可供遵循的步骤和方法,对学生的数学综合素养提出了更高的要求。解决这类问题,需要学生能够发现、选择和利用问题中的数学信息。例如学生通过观察,发现可把第二幅图中“一件T恤和两杯饮料看作一个整体76元”代入第一幅图求出T恤单价,这是解答这道题目的关键处。此题通过图形的信息,设立适当的未知数,能够把求物品的单价问题化为方程简单解决。
综上所述,小学数学试卷命题设计应体现学科特点,每一道命题就像一张张“身份证”,教师要善于从培养学生良好数学素养的角度编制它们,编制时要考虑它的适合性、丰富性和独创性,以此有效地发挥命题在促进学生数学思考方面的功能作用,从而能更好地拓展学生的思维,提高学生解决问题的能力,提升学生的数学素养。因此,教师在命题设计的创新上要有所作为,使课程的多元目标更多融入到书面测试评价之中,使小学数学命题能充分发挥评价的导向作用,从而促进学生的全面发展。
(浙江省长兴县实验小学 313100)

