下一代高精度卫星重力测量技术研究

廖 鹤,祝 竺,赵艳彬,李洪银

(1.上海卫星工程研究所,上海 201109; 2.华中科技大学 物理学院,湖北 武汉 430074;3.华中科技大学 地球物理研究所,湖北 武汉 430074)

下一代高精度卫星重力测量技术研究

廖 鹤1,祝 竺1,赵艳彬1,李洪银2、3

(1.上海卫星工程研究所,上海 201109; 2.华中科技大学 物理学院,湖北 武汉 430074;3.华中科技大学 地球物理研究所,湖北 武汉 430074)

以下一代高精度卫星重力测量为背景，针对低低卫卫跟踪模式与卫星重力梯度测量模式，论述了下一代低低卫卫跟踪和下一代重力梯度测量卫星方案。下一代低低卫卫跟踪重力卫星采用纳米级星间激光测距替代原微波测距，同时降低轨道高度以提高重力场敏感度。下一代重力梯度测量卫星采用原子干涉重力梯度仪替代静电重力梯度仪，原子干涉重力梯度仪在空间有超高的潜在灵敏度，可进一步提高卫星重力梯度测量的精度。同时，突破现有牛顿力学框架下的卫星重力测量技术，提出了基于广义相对论引力钟慢效应的卫星重力测量技术概念，卫星遍历地球周围空间时，通过测量星上时钟频率变化获取全球重力分布。仿真结果表明：三种新型高精度卫星重力测量技术可恢复200～305阶的全球重力场模型。

地球重力场； 卫星重力测量； 低低卫卫跟踪； 卫星重力梯度测量； 激光测距； 原子干涉； 引力钟慢效应

0 引言

卫星重力测量是以卫星为载体，利用卫星本身或所携带的载荷作为重力传感器(加速度计、精密测距系统、重力梯度仪等)，观测由地球重力场引起的卫星轨道摄动或直接测量地球重力场有关参量，以这些数据资料确定地球重力场分布的方法和技术[1]。卫星重力测量具有高效、高精度、全天候、全球覆盖的特点，是获取全球重力场最有效的手段之一，并得到了迅速发展与应用。21世纪以来，欧美国家先后通过卫星跟踪卫星技术与卫星重力梯度测量技术成功获得了高精度的地球重力场模型。卫星跟踪卫星技术是指星间的精密定位跟踪，分为两种模式：一种是高低卫卫跟踪模式(SST-HL)，通过高轨卫星(GPS)跟踪低轨卫星的轨道摄动确定地球的扰动重力场，如2000年发射的CHAMP卫星，将全球重力场恢复至70阶左右(对应空间分辨率285 km)；另一种是低低卫卫跟踪模式(SST-LL)，通过对两颗低轨卫星间的精密测距或测速获取地球重力位的变化信息，反演出地球重力场的位系数，如2002年发射的GRACE卫星，将全球重力场恢复至120阶左右(对应空间分辨率166 km)，同时测量了重力场的时变信息[2-3]。卫星重力梯度技术(SGG)则是利用星载重力梯度仪直接测量轨道处的重力梯度张量获取地球重力场信息，如2009年欧空局发射的GOCE卫星，将全球静态重力场恢复至200阶左右(对应空间分辨率100 km)[4]。但这些已有的重力场模型精度仍无法满足现代大地测量学、固体地球物理学、海洋学、冰川学等相关学科对空间分辨率50～100 km(对应200～400阶)的全球重力场模型的迫切需求，该波段的全球重力场模型有待进一步完善[5]。

低低卫卫跟踪模式与卫星重力梯度技术两者都涵盖了高低卫卫跟踪模式，因此国内外关注的焦点集中在GRACE，GOCE卫星上。基于GRACE，GOCE卫星对全球中长波静态重力场和长波时变重力场测量的巨大贡献，国内外对下一代更高精度的卫星重力测量技术进行了大量研究：文献[6]针对下一代的GRACE卫星进行了系统仿真；文献[7]提出了下一代基于原子干涉技术的卫星重力梯度测量方案；文献[8-9]对新一代GRACE卫星的反演重力场的精度进行了评估，并对我国将来重力卫星计划的实施提出了建议；文献[10]对下一代基于星载原子干涉的重力梯度测量技术进行了精度预测与应用前景分析。在该背景下，本文分别基于低低卫卫跟踪模式与重力梯度测量模式，论述了下一代卫星重力测量的发展趋势和技术特点，并基于目前原子钟的发展现状，提出了基于引力钟慢效应的卫星重力测量新概念，为未来更高精度的卫星重力测量计划提供技术参考。

1 下一代高精度卫星重力测量技术

1.1 基于低低卫卫跟踪模式的卫星重力测量

低低卫卫跟踪模式采用低轨双星测量，其基本测量原理主要是通过对两颗低轨卫星间的精密测距或测速获取地球重力位的变化信息，从而反演出地球重力场的位系数：高精度的星间测距系统测量低轨两颗卫星间的距离与速度变化，从而获得包括引力和非引力(大气阻尼、太阳光压等)共同引起的轨道总摄动，而非引力用高精度加速度测量，在重力场反演中扣除，最终得到待测的重力信息，即

gorbit=Ftotal/msc-Fng/msc.

(1)

式中：Ftotal为引力和非引力引起的轨道总摄动；Fng为大气阻尼、太阳光压等非引力；gorbit为轨道处的重力加速度；msc为卫星质量。

图1 GRACE卫星Fig.1 GRACE mission

GRACE卫星是低低卫卫跟踪模式的典型代表。1998年，NASA宣布实施GRACE计划[11]。该计划由两颗相同的低轨卫星组成，2002年3月17日同时发射至高度约500 km、偏心率0.004、倾角约89°、长半轴6 876 km的近极圆轨道，两星质量均为487.2 kg，相距220 km，如图1所示。GRACE卫星搭载的关键载荷有：SuperSTAR高精度静电加速度计、微波测距系统、星载GPS接收机、星敏感器和激光向后反射镜。星载GPS接收机结合高轨全球定位系统GPS和地面站以厘米级精度确定卫星轨道；激光向后反射镜与人卫激光地面站结合完成卫星与地球间的精确测距，用于校准GPS精确定轨；K波段以微米量级的测距测速精度测量由地表重力异常引起的星间距变化；加速度计以3×10-10m/(s2·Hz1/2)的精度测量卫星受到的大气阻尼、太阳光压等非保守力；星敏感器以角秒级的精度精确提供卫星的姿态信息。

GRACE卫星在轨飞行十多年，高精度地探测了地球重力场的中长波信号及其时变(2～120阶)，其得到的重力场信息超出此前30年的总和。鉴于GRACE卫星对全球中长波静态和时变重力场测量的巨大贡献，NASA提出了下一代GRACE Follow-on低低卫卫跟踪计划[6、12-13]。由于GRACE卫星对重力场的测量精度主要受限于星间测距精度，因此GRACE Follow-on旨在GRACE卫星的技术基础上，采用纳米级的星间激光测距技术替代原微米级的微波测距，同时缩短星间距，降低轨道高度(增加无拖曳控制系统对低轨大气阻尼进行补偿，用于延长卫星寿命、维持轨道高度)，以提高中高频重力场

的感测精度，如图2所示。NASA预计GRACE Follow-on得到的静态和动态地球重力场的精度将较GRACE至少高1个量级[8]。GRACE Follow-on与GRACE卫星技术参数的比较见表1[8-9]。

此外，ESA也针对下一代低低卫卫跟踪重力测量，提出了NGGM，E. MOTION等计划[9、14]。NGGM计划用于测量全球重力场变化信息，研究地球内部物质变迁。NGGM计划预计星间测距精度20 nm/Hz1/2，加速度计对非保守力测量精度预计为10-11m/(s2·Hz1/2)，星间距75～100 km。因该计划的其中一项目标要测量大气活动，而大气密度的变化很大程度由太阳活动决定(周期11年)，故NGGM计划提出可供参考的设计寿命为11年。E.MOTION计划采用钟摆式轨道，轨道高度373 km，星间距200 km，激光测距精度50 nm/Hz1/2，加速度计对非保守力测量精度10-12m/(s2·Hz1/2)，同时采用冷气与离子推进步补偿大气阻尼，卫星寿命不少于7年。其科学目标是时变地球重力场测量空间分辨率优于200 km，时间分辨率优于1个月，大地水准面精度优于1 mm。

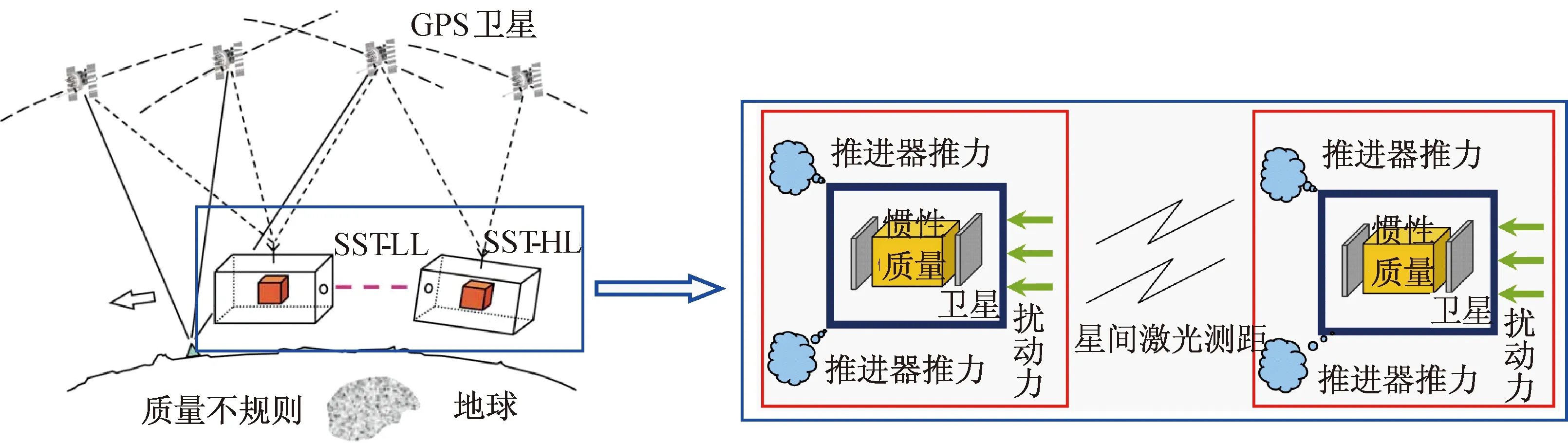
图2 基于星间激光测距的低低卫卫跟踪重力测量方案Fig.2 SST-LL based on laser ranging

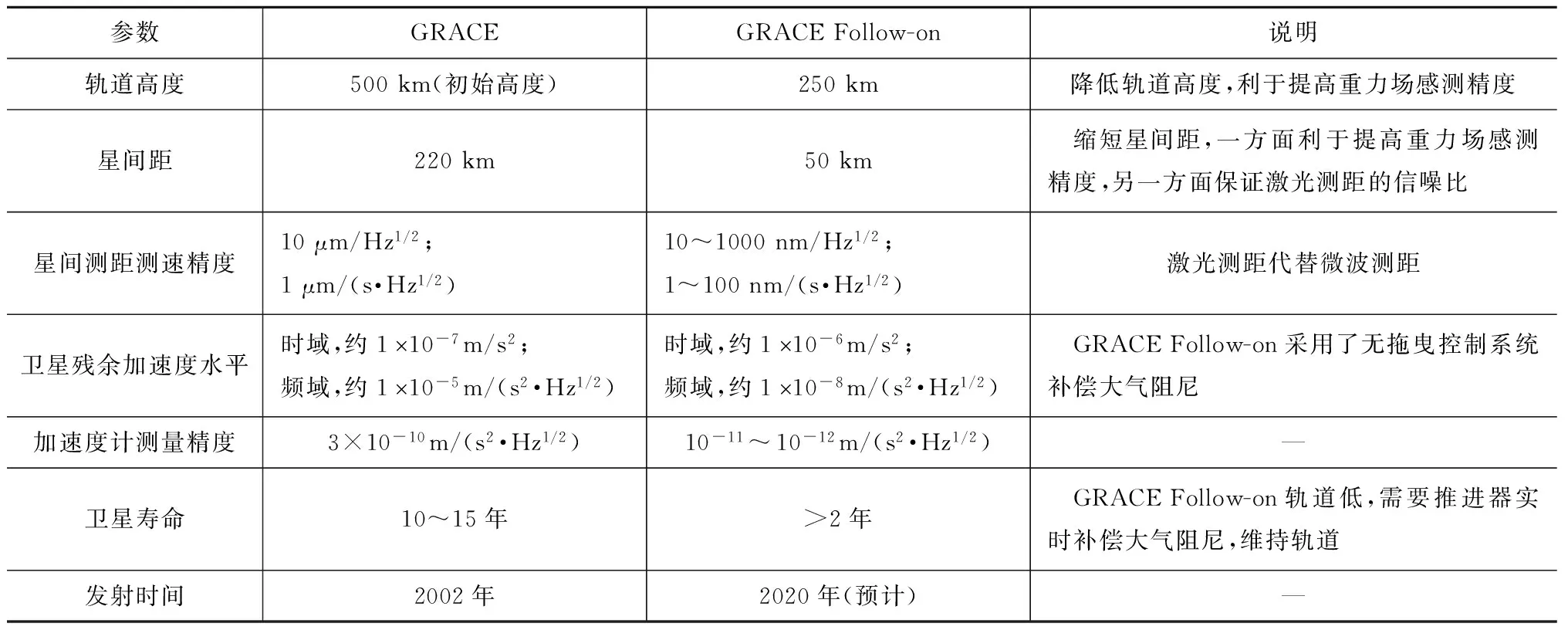
参数GRACEGRACEFollow-on说明轨道高度500km(初始高度)250km降低轨道高度,利于提高重力场感测精度星间距220km50km 缩短星间距,一方面利于提高重力场感测精度,另一方面保证激光测距的信噪比星间测距测速精度10μm/Hz1/2;1μm/(s·Hz1/2)10～1000nm/Hz1/2;1～100nm/(s·Hz1/2)激光测距代替微波测距卫星残余加速度水平时域,约1´10-7m/s2;频域,约1´10-5m/(s2·Hz1/2)时域,约1´10-6m/s2;频域,约1´10-8m/(s2·Hz1/2) GRACEFollow-on采用了无拖曳控制系统补偿大气阻尼加速度计测量精度3×10-10m/(s2·Hz1/2)10-11～10-12m/(s2·Hz1/2)—卫星寿命10～15年>2年 GRACEFollow-on轨道低,需要推进器实时补偿大气阻尼,维持轨道发射时间2002年2020年(预计)—

1.2 基于卫星重力梯度模式的卫星重力测量

卫星重力梯度测量的原理是利用定位于卫星质心处的重力梯度仪，基于差分加速度的测量原理，用加速度计高精度测量卫星轨道高度处不同两点所受到加速度差，再除以这两点的距离，得到轨道高度处重力加速度的变化值即重力梯度。但在这样的差分测量中，会混入卫星角速度的影响，因此需予以扣除，则

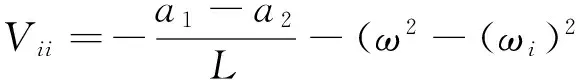
(2)

式中：Vii为待测的重力梯度值；a1，a2为不同两点的加速度计输出；L为两点的距离；ω为卫星角速度，且ω2=(ωx)2+(ωy)2+(ωz)2；ωi为卫星i轴的角速度，i=x，y，z。

人类第一颗基于卫星重力梯度测量技术模式的GOCE卫星计划，于1999年正式启动，2009年3月17日发射。它采用卫星重力梯度的测量模式，通过由6个静电加速度计构成的星载静电式重力梯度仪直接测量出轨道高度250 km处重力位的二阶导数，如图3所示。该测量模式可将重力位的球谐系数放大约l2倍(此处：l为重力位球谐系数展开的阶数)，有效地抑制因轨道高度上升而导致的重力场信号快速衰减，能感应地球重力场的高阶信息，提升重力场模型的测量精度。在以前卫卫跟踪模式的基础上，GOCE卫星将全球重力场探测的空间分辨率提升至100 km左右(200阶)。

由于GOCE卫星轨道高度较低，用于补偿大气

阻尼的推进剂容量有限，已于2013年结束寿命。ESA充分肯定了GOCE卫星对重力场模型精度提高的贡献[4]。但由于GOCE卫星核心载荷静电式重力梯度仪精度受低频噪声、动态范围等因素的限制，提升空间有限。ESA在2008年提出了未来可发展基于星载原子干涉技术的下一代卫星重力梯度测量技术。原子干涉重力测量技术目前处于地面实验阶段，其主要采用冷却囚禁原子的方式，Raman激光与冷原子相互作用，完成原子干涉，通过干涉条纹获得地面重力加速度的信息，如图4所示。其测量灵敏度与激光脉冲间隔T的平方成反比，由于地面存在重力加速度1g，因此受仪器尺寸的限制，T一般只能为数百毫秒；在空间微重力环境中，原子接近悬浮状态，间隔T可较易增大到秒甚至数十秒的量级，具有非常大的优势：一方面可显著提高星载重力测量精度，另一方面能有效缩短作用区真空腔长度，利于星载装置的小型化。此外，NASA量子科技团队在2002年也提出了利用星载原子干涉技术实现卫星重力梯度测量的设想，并指出测量分辨率至少较GOCE卫星高1个量级，且JPL在NASA的支持下已研制了便携式星载原子干涉重力梯度仪[15-16]。

静电式与原子干涉式的卫星重力梯度测量性能比较见表2[7、15]。

2 基于引力钟慢效应的卫星重力测量新概念

从前文论述可知：目前已发射成功及未来规划的各种卫星重力测量计划均基于牛顿力学框架。受传统惯性测量仪器加工精度、仪器属性、测量模型等固有因素的限制，牛顿力学框架下的卫星重力测量精度已接近极限，提升空间有限。随着科技的进步，人类在高精度计时领域取得了飞速发展，光晶格钟是2002年以来国际计量科学发展的一个新热点，其代表有锶原子光钟、汞离子光钟等。2015年初，日本东京大学与理化学研究所联合研究小组宣布，其开发的基于锶原子的光晶格钟计时精度达到每160亿年产生误差1 s，即准确度达到2×10-18，美国国家标准与技术研究所(NIST)和日本东京大学均指出，此高精度光钟为相对论力学框架下测量引力钟慢效应提供一种可能，将会在大地测量领域开辟全新的技术前景，并产生不可估量的效果[17-18]。在相对论力学框架下，基于引力钟慢效应的卫星重力测量新概念将明显提升重力场测量精度。

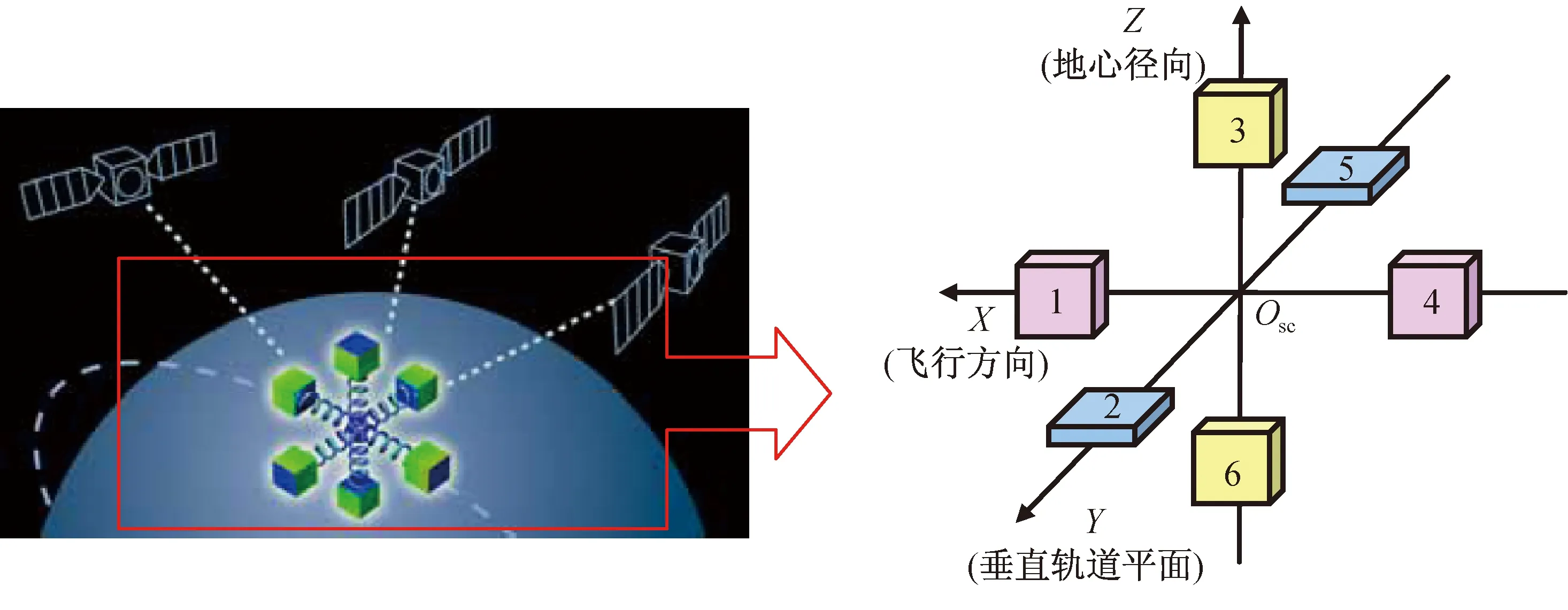
图3 GOCE卫星Fig.3 GOCE mission

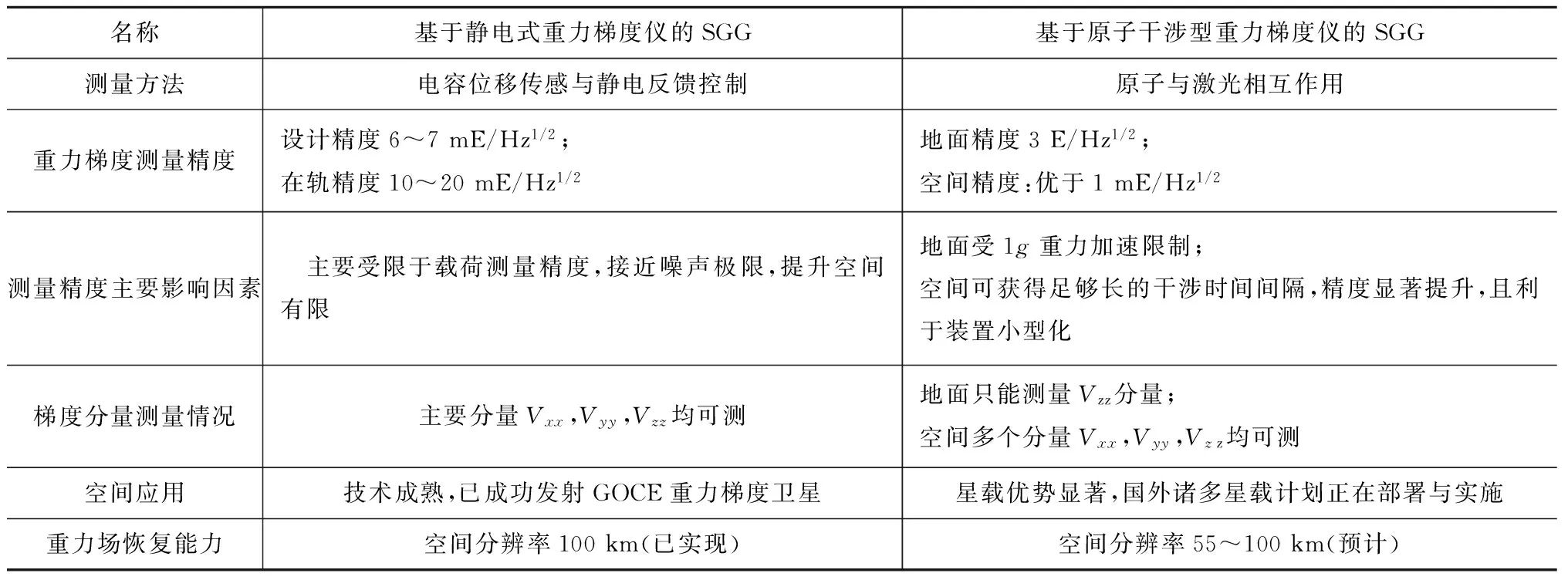
名称基于静电式重力梯度仪的SGG基于原子干涉型重力梯度仪的SGG测量方法电容位移传感与静电反馈控制原子与激光相互作用重力梯度测量精度设计精度6～7mE/Hz1/2;在轨精度10～20mE/Hz1/2地面精度3E/Hz1/2;空间精度:优于1mE/Hz1/2测量精度主要影响因素 主要受限于载荷测量精度,接近噪声极限,提升空间有限地面受1g重力加速限制;空间可获得足够长的干涉时间间隔,精度显著提升,且利于装置小型化梯度分量测量情况主要分量Vxx,Vyy,Vzz均可测地面只能测量Vzz分量;空间多个分量Vxx,Vyy,Vzz均可测空间应用技术成熟,已成功发射GOCE重力梯度卫星星载优势显著,国外诸多星载计划正在部署与实施重力场恢复能力空间分辨率100km(已实现)空间分辨率55～100km(预计)

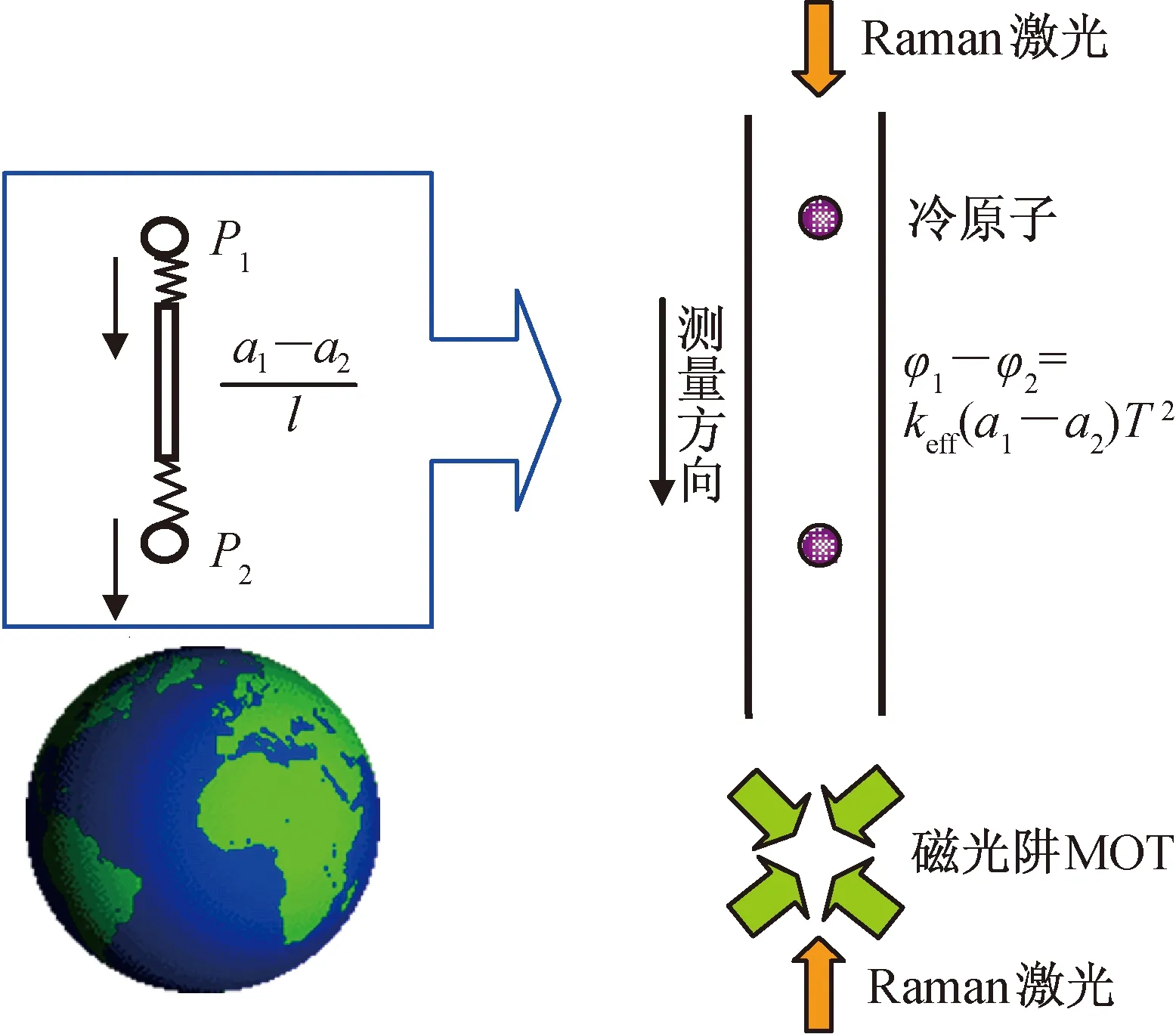
图4 基于原子干涉技术的卫星重力梯度测量方案Fig.4 SGG based on atom interference

根据广义相对论原理，任何质量会导致时空弯曲，时空弯曲会产生引力钟慢效应，即在引力场中，引力越强的地方，时间流逝越慢。即引力钟慢效应，具体测量原理为：考察沿地心径向相距一段位移的两点A、B(设其中点B为参考基准点)，它们分别与地心相距rA，rB，当两点距离差值为Δh=rA-rB时，设位于参考基准点位置的引力场强为g，如果在这两点放置两个高精度时钟，假设在参考基准点位置B的时钟经历ΔτB的时间内，另一时钟走了ΔτA的时间，那么两点时钟读数的差值Δt满足

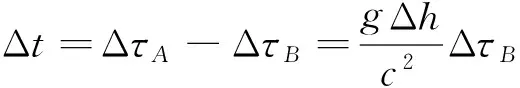
(3)

式中：c为光速[19]。基于上述原理，可通过时钟读数的差异Δt测出重力加速度g，有

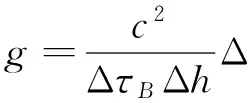
(4)

因此，将这种高精度的时钟置于重力场中，可检测到时钟频率的变化，且在地球的不同地方，能检测出这种快慢效应的差异。为此，本文提出基于引力钟慢效应的卫星重力测量新概念：在卫星上放置高精度时钟，由于地球形状不规则且引力场分布不均匀，卫星在遍历地球周围空间时变化的引力场导致星上时钟频率变化，对比“基准时钟”，可推演出卫星轨迹各点的引力场，进而获得地球重力场的分布信息，如图5所示。该方案实现的关键是研制具有超高时间频率准确度的原子光钟，难点是高精度的时间频率比对技术。

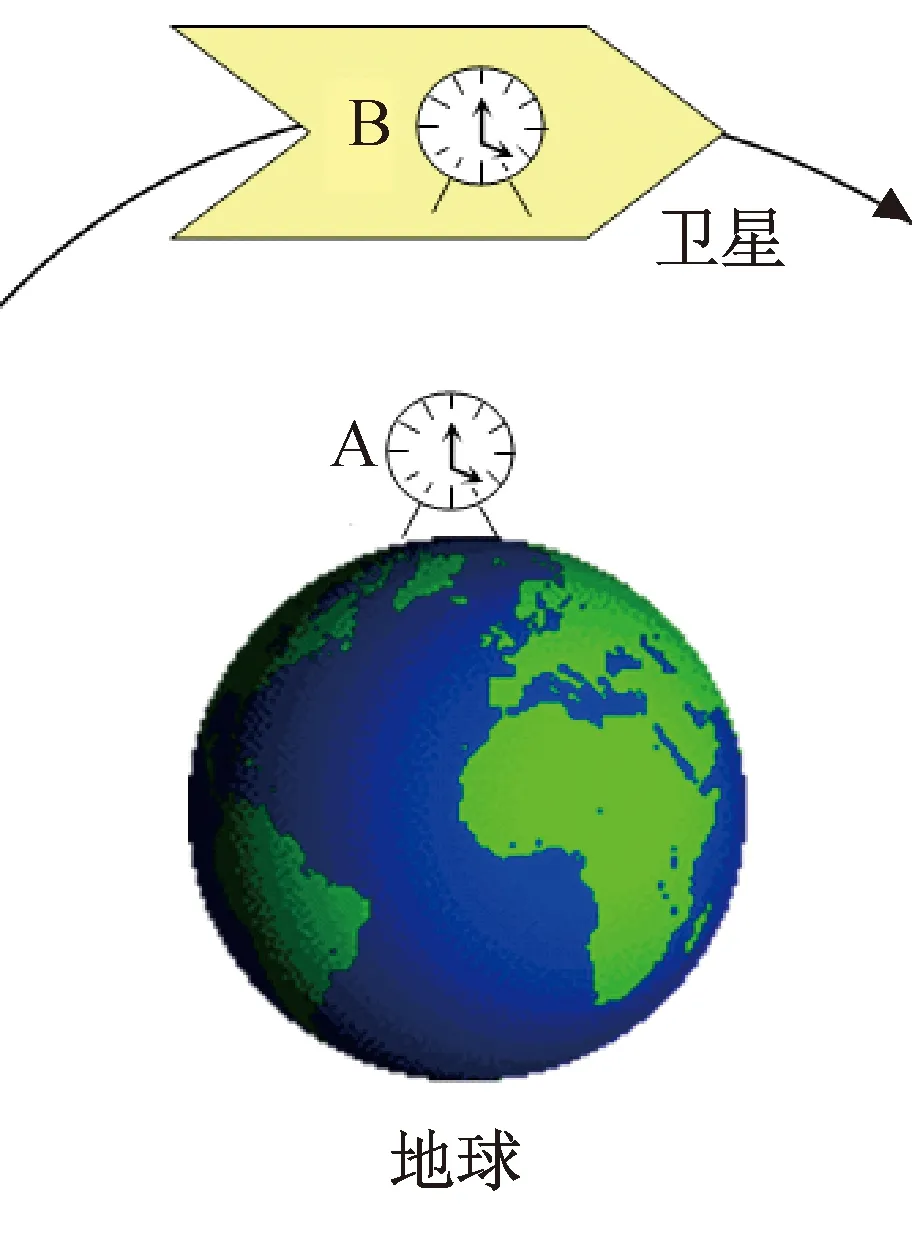
图5 基于引力钟慢效应的卫星重力测量概念Fig.5 Concept of satellite gravity measurement basedon effect of gravitational clock shift

3 下一代高精度重力场测量反演精度仿真

重力场测量的反演精度常用重力位球谐展开的阶数(对应空间分辨率)表征[8、20]。本文基于直接误差解析法，分别针对前文所述的基于低低卫卫跟踪模式的下一代卫星重力测量、基于卫星重力梯度模式的下一代卫星重力测量，以及基于引力钟慢效应的卫星重力测量三种未来技术恢复重力场的预期精度进行仿真与评估[20]。

国内外研究均针对下一代卫星重力测量，致力于其中关键技术的突破。如国外已实现了采用激光测距代替原有GRACE卫星采用的微波测距方式，实现了纳米级的测距精度[21]。基于此，本文代入的仿真参数是：下一代低低跟踪，星间距50 km，轨道高度250 km，星间测速精度1 nm/s，非保守力测量精度3×10-11m/(s2·Hz1/2)；下一代重力梯度测量，轨道高度250 km，原子干涉梯度仪分辨率1 mE/Hz1/2；引力钟慢重力测量，轨道高度250 km，时钟频率准确度2×10-18s/s，采样时间间隔10 s。仿真数据周期为8个月，频带内载荷测量噪声均设为白噪声，所得重力场位系数的误差阶方差如图6所示[7-8、15、17、20]。

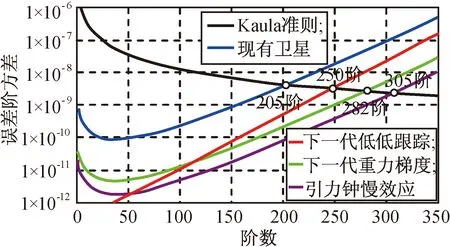
图6 不同卫星重力测量技术的重力场反演误差阶方差估计Fig.6 Expected error degree variance from differenttechnologies of satellite gravity measurement

由图6可知：现有的重力卫星可实现的重力场模型精度约205阶(对应空间分辨率100 km左右)；未来的卫星重力测量技术均可不同程度地改善重力场模型精度，预计基于低低卫卫跟踪模式的下一代卫星重力测量技术可将重力场恢复至250阶(对应空间分辨率80 km)，基于卫星重力梯度模式的下一代卫星重力测量技术可将重力场恢复至282阶(对应空间分辨率71 km)，基于引力钟慢效应的卫星重力测量可将重力场恢复至305阶(对应空间分辨率66 km)。具体数据见表3。

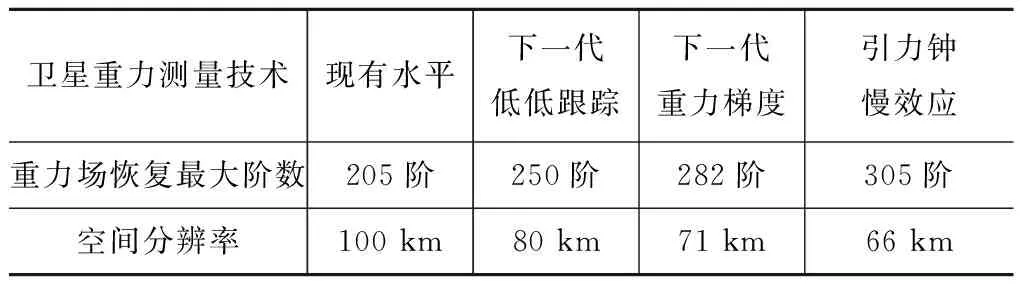
表3 未来卫星重力测量技术恢复重力场预期精度水平

由表3可知：下一代SST与SGG，以及本文提出的基于引力钟慢效应的卫星重力测量可完善200～305阶的全球重力场模型。未来可通过进一步降低轨道、提高载荷研制精度等途径完善305～400阶的全球重力场模型，这意味着将对卫星姿轨控、推进分系统，以及空间环境提出更严格的要求。

4 结束语

下一代卫星重力测量旨在现有重力卫星的基础上，进一步提升重力场模型精度，获取200阶以上的静态与时变重力场。本文阐述了基于SST-LL模式与SGG模式的下一代卫星重力测量方案与技术特征，仿真结果表明：基于纳米级激光测距技术的下一代低低卫卫跟踪重力测量与基于原子干涉技术的下一代卫星重力梯度测量预计将重力场反演的空间分辨率分别提升至80，71 km。本文突破现有牛顿力学框架下的卫星重力测量技术，提出了基于相对论引力钟慢效应的卫星重力测量新概念，预计可将重力场反演的空间分辨率进一步提升至66 km，为未来更高精度的卫星重力测量提供技术参考。该测量新概念还处于初步研究阶段，理论上对全球重力场的恢复精度有望突破300阶，但在工程实现中，需研制适于星载环境的高精度冷原子光钟，同时对星地时间同步提出了较高要求，后续研究有待深入开展。

[1] 许厚泽, 陆洋, 钟敏, 等. 卫星重力测量及其在地球物理环境变化监测中的应用[J]. 中国科学: 地球科学, 2012, 42(6): 843-853.

[2] REIGBER C, LÜHR H, SCHWINTZER P. CHAMP mission status[J]. Advances in Space Research, 2002, 30(2): 129-134.

[3] CHENG M K. Gravitational disturbation theory for intersatellite tracking[J]. Journal of Geodesy, 2002, 76: 769-185.

[4] RUMMEL R, YI W Y, STUMMER C. GOCE gravitational gradiometry[J]. Journal of Geodesy, 2011, 85(11): 777-790.

[5] ESA. The four candidate Earth explorer core missions-gravity field and steady-state ocean circulation mission[R]. ESA: SP-1233(1), 1999.

[6] LOOMIS B D, NEREM R S, LUTHCCKE S B. Simulation study of a follow-on gravity mission to GRACE[J]. Journal of Geodesy, 2012, 86(5): 319-335.

[7] YU N, KOHEL J M, KELLOGG J R, et al. Development of an atom-interferometer gravity gradiometer for gravity measurement from space[J]. Appl Phys B: Lasers and Optics, 2006, 84: 647-652.

[8] 郑伟, 许厚泽, 钟敏, 等. 基于GRACE Follow-On卫星重力梯度法精确反演地球重力场[J]. 地球物理学报, 2014, 57(5): 1415-1423.

[9] 郑伟, 许厚泽, 钟敏, 等. 国际下一代卫星重力测量计划研究进展[J]. 大地测量与地球动力学, 2012, 32(3): 152-159.

[10] 翟振和, 吴富梅. 基于原子干涉测量技术的卫星重力梯度测量[J]. 测绘通报, 2007(2): 5-6.

[11] KIM J. Simulation study of a low-low satellite-to-satellite tracking mission[D]. Austin: University of Texas, 2000.

[12] TAPLEY B, RIES J, BETTADPUR S, et al. GGM02-An improved Earth gravity field model from GRACE[J]. Journal of Geodesy, 2005, 79(8): 467-478.

[13] REIGBER C, SCHMIDT R, FLECHTNER F. An Earth gravity field model complete to degree and order 150 from GRACE: EIGEN-GRACE02S[J]. Journal of Geodynamics, 2005, 39(1): 1-10.

[14] Internal Thales Alenia Space. Assessment of a next generation mission for monitoring the variations of Earth’s gravity final report[R]. SD-RP-AI-0688, 2010.

[15] YU N, KOHEL J M, ROMANS L, et al. Quantum gravity gradiometer sensor for Earth science applications[C]// NASA Earth Science and Technology Conference 2002. Pasadena: NASA, 2002: Paper B3P5.

[16] MCGUIRK J M, FOSTER G T, FIXLER J B, et al. Sensitive absolute-gravity gradiometry using atom interferometry[J]. Physical Review A, 2002, 65: 033608.

[17] USHIJIMA I, TAKAMOTO M, DAS M, et al. Cryogenic optical lattice clocks[J]. Nature Photonics, 2015(9): 185-189.

[18] TAKAMOTO M, HONG F L, HIGASHI R, et al. An optical lattice clock[J]. Nature, 2005, 435: 321-324.

[19] 梁灿彬, 曹周键. 从零学相对论[M]. 北京： 高等教育出版社, 2013.

[20] CAI L, ZHOU Z B, XU H, et al. Analytical error analysis for satellite gravity field determination based on two-dimensional Fourier method[J]. Journal of Geodesy, 2013, 87: 417-426.

[21] YEH H C, YAN Q Z, LIANG Y R, et al. Intersatellite laser ranging with homodyne optical phase locking for Space Advanced Gravity Measurements mission[J]. Review of Scientific Instruments, 2011, 82: 044501.

Research on High-Precision Satellite Gravity Measurement Technology for Next Generation

LIAO He1, ZHU Zhu1, ZHAO Yan-bin1, LI Hong-yin2, 3

(1. Shanghai Institute of Satellite Engineering, Shanghai 201109, China;2. School of Physics, Huazhong University of Science and Technology, Wuhan 430074, Hubei, China;3. Institute of Geophysics, Huazhong University of Science and Technology, Wuhan 430074, Hubei, China)

Towards to the high-precision satellite gravity measurement for the next generation, the schemes of satellite-to-satellite tracking in the low-low mode and satellite gravity gradiometry for the next generation respectively were described. According to the satellite-to-satellite tracking in the low-low mode for the next generation, laser ranging technique with nm level will be used instead of microwave ranging technique, and the satellite altitude will be reduced to improve the sensitivity. Atom-interference gravity gradiometer will be adopted in satellite gravity gradiometry for the next generation instead of electrostatic gravity gradiometer. The ultra potential sensitivity of the atom-interference gravity gradiometer in space will significantly improve the accuracy of satellite gravity gradiometry. Besides, a new concept of satellite gravity measurement based on the effect of gravitational clock shift was proposed in this paper. The Earth’s gravity field will be precisely mapped through measuring the clock’s fractional frequency difference in various areas of the Earth around the track. This new concept is different from the technologies in Newton mechanics. The simulation results showed that the precision of the three kinds of satellite gravity measurement technologies for the next generation would be expected to improve the knowledge of the global Earth’s gravity field up to 200～ 305 order.

Earth’s gravity field; Satellite gravity measurement; Satellite-to-satellite tracking in the low-low mode; Satellite gravity gradiometry; Laser ranging; Atom interference; Effect of gravitational clock shift

1006-1630(2016)06-0102-07

2016-07-14；

2016-07-30

国家自然基金资助(41504034)

廖 鹤(1984—)，男，博士，高级工程师，主要研究方向为飞行器总体设计。

祝 竺(1985—)，女，博士，主要研究方向为卫星重力测量。

P223.6

A

10.19328/j.cnki.1006-1630.2016.06.015