求解排课问题的遗传蚁群混合算法

◎王丽红 刘平 于光华

求解排课问题的遗传蚁群混合算法

◎王丽红 刘平 于光华

针对排课问题，本文将遗传算法和蚁群优化算法融合，提出了一种遗传蚁群混合的优化算法。首先利用遗传算法产生初始信息素的分布，在运用蚁群算法求精确解。实验表明该算法取得了良好的适应度值和时间性能。

排课问题涉及到教师、教室、班级、课程、时间等诸多因素，是一个处理起来相当复杂的优化决策问题。排课问题已被证明是一个NP完全问题，也是一个很有研究价值的实际问题。

文献提出了一种新型的解决排课问题的离散粒子群算法，在三维空间中建立模型，并引入了冲突检测及变异等操作。文献提出了自适应遗传算法，该算法采用三维编码方案，并在交叉概率和变异概率、适应度函数、初始种群的生成等方面都进行了设计和优化。文献应用蚁群遗传算法进行排课研究。在本文将遗传算法与蚁群算法融合来研究排课问题。

排课问题描述

问题描述

排课问题实际上是一个五维空间上的组合优化求解问题。五维是指教室、教师、班级、课程、时间，要实现的目标是上述五元素的最优化配置，对于这一类组合优化问题要寻求一种合理的近似最优解。

约束条件

排课方案必须满足两大类约束：硬约束是衡量一个排课方案是否可行的标准，软约束是衡量一个排课方案优劣的标准，而反映一个排课方案优劣的标准有多种情况。

硬约束是指在排课过程中必须遵守的规则，一般包含以下几个方面：同一时间段内，一位教师不能排一门以上的课程，不能占有一个以上的教室；同一时间段内，一个班级不能上一门以上的课程；同一时间段内，一个实验室不能排一门以上的课程；教室能够容纳上课班级的学生人数。

软约束条件是指在排课方案中可以满足但又可以不完全满足的条件，根据各学院情况不同而有所差别，包含以下几个方面：专业相关的重要课程尽量安排在较好的教学时间段；多学时的课程每周的安排要错开（学时大于等于4课时，能够尽量隔天排一次课）；一周内每天课时尽量平均；教室利用率高，上课班级人数尽量接近教室可容钠人数。

排课问题数学模型

排课问题中设计的实体集合有教师、教室、班级、课程、时间，具体设定如下：教室集合表示第i个教室；教师集合表示第i位教师；班级集合表示第i个班级；课程集合表示第i门课程；时间集合表示第i个时间段。

遗传蚁群算法

算法基本思想

遗传算法在搜索初期具有较高向最优解的收敛速度，但是达到一定时刻后不能有效利用系统中的反馈信息，使搜索具有盲目性，导致求解速度会明显降低。由于信息素匮乏，蚁群算法在初期搜索速度缓慢，当信息素累积到一定程度之后，蚁群算法求解效率会迅速提高。而遗传蚁群混合算法的基本思想是，首先采用遗传算法产生初始信息素的分布，当遗传算法达到一定迭代次数或群体中向最优解的进化速率低于一定程度时结束遗传算法，应用蚁群算进行最优解的求解。如图1所示。

遗传算法

编码。针对排课问题的特点，使用三维数组对排课信息进行保存，具有编码和解码都很直观，方便冲突检测，算法的复杂度低等优点。

编码和适应度函数。对于适应度函数，我们主要考虑软约束：

i程，应尽量隔一天以上再安排。若某门课程间隔 天上课效果的权值为该门课程的重要性权值为 ωi，优化目标：

遗传操作。在标准遗传算法中,交叉概率和变异概率是固定不变的。为了保持种群的多样性，避免出现早熟和局部收敛现象，本文根据遗传操作前后最优染色体适应度值的变化情况,对交叉概率和变异概率采用自适应调整策略。

交叉概率调整策略：交叉操作前参与交叉的染色体中,最优染色体的适应度值为交叉后所得最优染色体的适应度值为原来交叉概率为 pc,则调整后交叉概率为

图1 遗传蚁群算法速度时间曲线图

变异概率调整策略:变异操作前参与变异的染色体中,最优染色体的适应度值为变异后所得最优染色体的适应度值为原来变异概率为则调整后变异概率为:

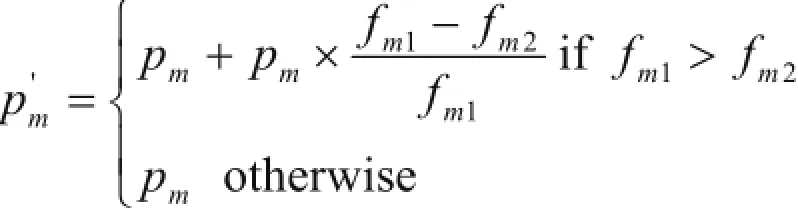
蚁群优化算法

信息素更新

排课问题即解决S × R →{L,T,C}的关系，为了将蚁群算法应用到其中，将排课问题转化为{S, R}与{L,T,C}构成的二分图的最大匹配问题。本文采用蚁周系统模型, 第K 只蚂蚁完成一次周游后, 路径(i, j)上的信息素增量定义为:

其中 LK为第K只蚂蚁完成本次周游所经历的路径长度，Q为常数。在每一只蚂蚁完成一次周游后,路径上新的信息量为:

目标结点的选择策略

在蚂蚁周游过程中,蚂蚁K由节点i选择到节点 j的概率为:

其中allowedk表示蚂蚁K下一步允许选择的节点。

求解排课问题的遗传蚁群混合算法

下面详细描述遗传蚁群混合算法的执行过程。

1.定义适应度函数和目标函数，设置遗传算法控制参数。

2.随机产生初始种群 P(g)，g=0。

3.计算 P(0)中每个个体的适应度值。

4.进行遗传选择、交叉、变异操作，直到满足遗传算法的结束条件:

(1)根据个体适应度值及选择策略确定 P(g)内所选择的个体。

(2)交叉操作：对所选择的2个父体执行交叉操作，并将所得 的2个后代插入P(g+1) 中，并计算个体适应度值，同时记录交叉操作前后最优染色体的适应度值1cf 、2cf 。

(3)变异操作:对所选择的2个父体执行变异操作，并将所得的2个后代插入P(g+1)中，并计算个体适应度值，同时记录变异操作前后最优染色体的适应度值1mf 、2mf 。

(4)根据遗传操作前后最优染色体的适应度值调整交叉概率pc和变异概率 pm。

5.从 P(g)中选择适应能力强的部分个体放入优化解集合。

6.对于优化解集合中的每个优化解，将遗传算法的求解结果转换成蚁群算法信息素初值设置。

7.初始化蚁群优化算法控制参数，设置蚁群算法结束条件。

8.反复执行下列操作，直至满足蚁群算法结束条件：

(1)在二分图顶点处放置 m 只蚂蚁;

(2)计算蚂蚁K由节点i转移到节点j的概率，并根据计算结果选择下一步转移的节点j，将j在中删除。

(3)判断蚂蚁K是否遍历完所有的节点，若是，表示蚂蚁K完成一次周游，执行下一步；反之，返回(2)。

(4)判断是否所有的蚂蚁均完成周游，若是，执行下一步；反之，返回(2)。

(5)计算所得 m种周游方案的适应值,并从中选择最佳方案的蚂蚁。

(6)对信息素值进行更新，返回(1)。

结果分析

算法用vc++实现，为验证遗传蚁群混合算法在实际排课问题中的优化效果，分别用遗传算法、蚁群算法和遗传蚁群混合算法进行了模拟实验。三种算法所用的平均运行时间对比图如图2所示。

图2 三种算法运行时间比较

三种算法平均适应度值对比图如图3所示。

图3 三种算法适应度值比较

由模拟实验结果可知，遗传蚁群混合算法的运行时间要较遗传算法、蚁群算法长一些， 但是适应度要远远高于遗传、蚁群算法，利用遗传蚁群混合算法产生的排课方案能够使得各门课时间段分布均匀，能够满足教学需要。

（作者单位：黑河学院计算机与信息工程学院）

黑龙江省大学生创新创业训练计划项目《基于c/c++的智能排课软件》，项目编号201513744024