μ-PPT等离子体电子密度氢光谱诊断技术
王尚民,张家良,张天平,冯杰,郑茂繁,黄永杰
1.兰州空间技术物理研究所,兰州730000 2.大连理工大学,大连116024
μ-PPT等离子体电子密度氢光谱诊断技术
王尚民1,张家良2,*,张天平1,冯杰1,郑茂繁1,黄永杰1
1.兰州空间技术物理研究所,兰州730000 2.大连理工大学,大连116024
为了能够表征推进剂烧蚀产物的有效加速度及推进剂利用率,需要更准确地测量等离子电推力器(PPT)内等离子体的基础状态参数(电子密度、电子温度),提出了基于光谱线Stark加宽分析,提高PPT放电通道内等离子体电子密度诊断精度的一种方法。针对来自于推进剂的C原子谱线,测量线型函数和半高全宽(FWHM),可以计算电子密度,但要求等离子体电子密度需足够高。当电子密度低于1016cm-3,此方案的测量可靠性便显著降低。为此,提出了通过向放电空间引入微量含氢气体作为示踪剂,测量H原子谱线线型和半高全宽进而诊断电子密度的技术方案。相比于C原子谱线诊断方案,氢方案可以大幅度提高电子密度测量下限至1013cm-3,因此能够显著改进电子密度测量准确性和可靠性。
电子密度;Stark展宽;H原子谱线分析;等离子体电推力器;高精度测量
作为最早提出的电推进技术之一,微脉冲等离子体电推力器(Micro-Pulsed Plasma Thruster, μ-PPT)具有较高的技术成熟度,并且因其体积小、质量轻、结构简单、精确脉冲调节以及小功率下高比冲等优点,可满足微小卫星对推进系统提出的轻质量、低功耗及精确可控等严苛要求,近年来逐渐成为关注和研究的热点[1]。
μ-PPT等离子体电子密度诊断,可以确定推进剂烧蚀产物的有效加速度以及推进剂利用率。
电子密度测量的常用方法包括:发射光谱法、微波干涉法、Thomson散射法和探针法等[2-5]。微波干涉法和Thomson散射法的设备复杂,造价高,不适于一般工程应用。实际工程领域中多采用探针法和发射光谱法诊断等离子体密度。
μ-PPT的放电形式为电流脉冲峰值可达10 k A的高电流短脉冲真空弧放电[6],放电过程的不稳定和辐射对于探针测量系统形成强烈的电磁干扰,制约了探针技术的适用性。此外,放电产生的等离子体时间较短,仅在数微秒至几十微秒间[6],使用探针扫描技术难度极大。因此,μ-PPT等离子体电子密度更适宜于采用无直接接触、抗电磁干扰的发射光谱法进行测量。基于发射谱线的Stark加宽与电子密度的相关性,测量发射光谱可以计算电子密度。谱线的Stark效应与电子温度相关性很弱,而与电子密度紧密相关。因此,无论是达到热力学平衡的准稳态等离子体还是脉冲等离子体,都可以利用Stark展宽进行电子密度诊断[7-8]。
Stark加宽法分为H谱线展宽法和非H加宽法。非H谱线的Stark展宽是二阶非线性Stark效应产生的,比氢原子的一阶Stark效应加宽小得多。因此,应选用H谱线的Stark加宽进行电子密度测量。对于不含H的等离子体,则一般通过在气体中加入少量H2或碳氢气体来产生H原子谱线[9]。
由于μ-PPT推进剂不含有氢元素,国内外均采用C原子Stark加宽测量来计算μ-PPT电子密度[10-11]。鉴于C谱线的二阶Stark加宽效应很微弱,μ-PPT体系的电子密度必须足够高,起码不低于1016cm-3,才能得到足够的诊断测量精度。
一般情况下,μ-PPT放电的电子密度很难高于1016cm-3,因此C原子Stark加宽测得的电子密度精度很低。针对此问题,本文分析了向μ-PPT放电空间中加入微量H2来产生H原子, H谱线展宽测量电子密度的可行性。相比C谱线,该方案可以有效提高测量精度,因为氢Stark加宽测量要求电子密度不低于1013cm-3即可。
1 Stark加宽测量电子密度原理
等离子体中的中性原子和离子的辐射谱线线型,会受到它们所在的等离子体环境因素的影响,这些影响因素包括等离子体中的电子、原子、离子与辐射粒子碰撞过程,以及准静态微电场对辐射粒子能级系统的扰动。这些相互作用均导致谱线的加宽和峰值位置移动。因此试验测得的谱线形状,原则上携带了该等离子体状态信息,其中电子、离子的作用导致的谱线加宽和移动,就称为谱线的Stark加宽和移动。因此等离子体谱线的Stark加宽反映了等离子体密度和温度信息。
1.1 H原子Stark加宽方案
氢原子方案不仅可以提高电子密度测量下限并且还具有较高的准确度。氢原子和类氢原子的Stark效应之所以能够取得如此好的准确度,是因为氢原子和类氢元素的能级结构可以进行精确的理论计算,而且氢原子具有最高的对称性。氢原子的对称性导致角量子数偶然兼并,使得其成为惟一的线性Stark效应体系,Stark效应强度最显著。其他元素的Stark效应由于都是二阶效应,效应强度比氢原子至少弱两个量级。所以,任何等离子体中只要能够加入氢原子或类氢原子,均可以利用氢元素的Stark加宽以更高精度进行等离子体密度诊断。Stark加宽效应是一种几乎完全决定于等离子体电子密度的过程。
氢原子的巴耳末线系具有典型的斯塔克加宽轮廓,位于可见区,容易测量,在电子密度诊断中备受重视。Hγ谱线激发能级较高,光谱强度小,导致结果误差较大[12]。Hα和Hβ在不同情况下,各具有优势。但最常用的氢谱线就是Hβ谱线,因为这条线的强度是巴尔末线系中的第二峰高谱线,而且位于比较容易探测的光谱区。Hβ与Hα相比,Hβ具有更显著的加宽效应,比如当电子密度为1017cm-3时,Hα、Hβ谱线的半高全宽为1.0 nm、4.6 nm。与Hα相比,Hβ谱线所有组成分量均发生Stark移动,所以自吸收效应特别小,因此不存在自吸收加宽的干扰。另一方面,Hβ谱线轮廓的理论计算也达到了最高精度。不过,如果无法测量到足够强度的Hβ,利用Hα谱线线型也是获得电子密度的不错方案,因为一般等离子体条件下, Hα谱线的强度要比Hβ大许多,虽然其线型理论计算精确度比利用Hβ低一些,而且也存在比Hβ更大的精细结构加宽。
为了计算电子密度,需要把谱线轮廓和理论计算的谱线轮廓相比较。一种方法是比较两者的半高全宽(FWHM),找出半宽相同的理论线型,从而确定电子密度。另一种方法是把两者的整个轮廓曲线做比较,根据最小二乘原理找出与试验谱线轮廓最佳拟合的理论谱线轮廓来确定电子密度。由于半宽法比较简捷,且误差相差不大,所以广泛使用。
Stark加宽线型的理论计算非常繁琐, Griem提出了一种约化线型函数的方法[13-14],即引入约化波长10-13n2/3e,其中,λ0为谱线中心波长,ne是电子密度(单位m-3)。利用约化波长可以把Stark线型函数归一化成约化线型函数S(α),满足

Griem在电子温度为5 000 K、10 000 K、20 000 K、40 000 K,电子密度为1014cm-3、1015cm-3、1016cm-3、1017cm-3条件下对约化线型函数进行理论计算,并制成表格。在实际应用中,利用这些图表和内插法就可以求得任意电子密度和温度下谱线轮廓,与实测线型进行对比就可以求得电子温度和密度。对于一定范围的电子温度和电子密度,氢原子谱线的Stark加宽几乎可以视为Lorentz线型,其半高全宽就决定了谱线线型,这时可以直接利用半高全宽得到电子温度和密度。所以只要Stark加宽线型可以视为Lorentz线型,就可以简化Stark加宽计算电子密度的方法。图1是根据Griem的数值计算结果描绘的Stark线型宽度。从图中可以看出,在电子温度不高情况下,无论Hα还是Hβ,其Stark加宽都几乎与电子温度无关。

图1 不同等离子体温度下,Hα和Hβ半高全宽与电子密度的关系[15]Fig.1 Dependence of Hαand HβFWHM on the electron density at different plasma temperatures

两边取对数可以得到

当电子温度高于4 e V时,Hα的Stark加宽会与式(3)有明显偏离,所以在使用Hα时,需确保电子温度不高于4 e V。这样可以认为Stark加宽只与电子密度有关。
根据图1中的线性关系,可以看出所对应的等离子体条件下,α1/2基本为一个常数。对应于Hα和Hβ这个常数分别为:αα1/2=0.008,αβ1/2= 0.04。至此,只要能够试验测定氢原子谱线的stark加宽,就可以确定电子密度。
1.2 可能存在的谱线加宽机制及其分离方法
试验测量到的谱线加宽是多种加宽机制共同作用的结果,为了获得Stark加宽,必须弄清楚其他所有可能加宽机制并适当予以分离,才能得到Stark加宽。谱线加宽主要包含以下几种机制:
1)自然加宽。通常自然加宽很小,在10-5~10-4nm范围内,相对其他加宽要小2个量级,通常忽略。
2)共振加宽。共振加宽与基态粒子密度成正比,由于示踪H原子密度较低,因此,其共振加宽效应也很弱,在本方案中可忽略。
4)范德瓦尔斯加宽。碰撞加宽和范德瓦尔斯加宽都是短程相互作用产生的能级扰动的结果,只有在原子数密度高至一定程度,原子间的平均距离达到范德瓦尔斯力的有效作用程内,才能产生明显的加宽。大气压下的自由程与范德瓦尔斯作用程相当,均为微米量级,相应的数密度为1019cm-3,所以碰撞加宽与范德瓦尔斯加宽量级相同。
5)多普勒加宽。多普勒加宽是辐射粒子与检测器的相对运动引起的。当辐射粒子服从麦克斯韦速度分布时,辐射谱线轮廓为高斯线型并且只依赖于气体温度Tg(K)。多普勒加宽ΔλD大小为M为辐射原子的摩尔质量(g/mol)。多普勒加宽的线型为高斯线型,与其他加宽线型不同。在气体温度为10-4K时,可以计算出Hα相应的多普勒加宽为0.036 nm,可见氢原子可以产生足够大的多普勒加宽。不过,多普勒加宽仅体现在谱线线型的高斯成分中,不会影响Stark成分的分离解析。
6)谱仪加宽。也称为谱仪传递函数。好的光谱仪加宽线型一般是高斯型的,所以常用高斯型传递函数用作实测谱线线型的解卷积程序的核函数。高斯线型谱线的远波长侧通常下降得较慢,亦即高斯线型函数以波长为变量时,线型不是对称的。另一方面,由于粒子谱线的Stark线型在很好的近似下是洛仑兹型的。一般可以采用Voigt谱线函数作为实测谱线的模型函数,借助于解卷积分析方法从观测到的谱线导出Stark加宽宽度。
7)自吸收加宽。Hα和Hβ的下能级都是主量子数为2的激发态,其寿命很短,因此一般情况下,此能级上的粒子布居数不很高,没有显著自吸收效应,除非是在纯氢气环境的高密度放电场合,例如氢气电弧、核聚变装置中。不过,Hα和Hβ相比,Hα更容易发生自吸收,因为Hα跃迁辐射速率系数比Hβ的大5倍,所以使用Hα的线型分析时,更需要注重自吸收加宽。
综上所述,上述各类加宽机制中,5)、6)两种机制在Stark加宽分析需要加以考虑,其他机制均可以忽略,因为在所研究的微脉冲等离子体放电场合下,氢气不是放电的主要成分(共振加宽和自吸收加宽不重要),而且也是在真空条件下发生的(碰撞加宽和范德瓦尔斯加宽不重要)。虽然放电的开始阶段,瞬时气压会比较高,碰撞加宽和范德瓦尔斯加宽会比较明显,但是考虑到试验测量的光谱是空间平均光谱,空间的气压分布不均匀,只是在推进剂附近很小的体积内气压高,其他区域内气压都很低,所以空间平均的结果使得这两类与气压相关的加宽可以忽略。但是需要注意,如果能够实现空间分辨光谱测量,那么在推进剂附近等离子体区光谱中谱线的此两类加宽也必须分析。
2 成像装置及光谱系统
2.1 空间分辨成像光谱系统
对于固体烧蚀型PPT,常采用“弹丸模型”(Slug Model)[16]。该模型基本原理为:随着放电的开始,一部分固体推进剂被其表面的放电电弧烧蚀、电离,形成一个很薄的等离子体电流片,回路电流只能在电流片表面上很薄的一个层内流动,电流片在表面力及体积力的作用下以“弹丸”的形式向喷口加速喷出。电流片的质量通常视为恒定不变。这一模型在一定程度上有助于了解PPT工作物理过程。然而,采用高速相机测量的方法对固体烧蚀PPT等离子体进行研究,表明PPT等离子体并非以电流片存在而是呈弥散状。更进一步,放电空间中电流密度的测量表明,在整个放电周期内,放电电流及其自感电场是紧挨着推进剂表面,而不是沿着喷口方向通道上移动。通过烧蚀过程仿真也表明,PPT等离子体是一种弥散的等离子体区,而不是明确的电流片[10]。因此,可将PPT放电区看成多个电流片堆积而成,并可通过不同电流片的电子密度测量,进一步理解PPT运行物理机制。
基于上段分析,μ-PPT等离子体可认为是长方体形放电结构,如果直接用光纤对长方体形等离子体进行发射光谱测量,光源的发散角远大于光纤数值孔径,不仅会造成光信号的损耗,而且还不能进行空间分辨。因此,为了更高效率地收集发光并进行空间分辨测量,在等离子体放电区与收集光纤入口之间插入一个透镜,经透镜成像,将等离子体的发光会聚到光纤收集端口。光纤端面为圆形,由19根直径为0.19 mm的多模光纤排列所成,直径为1 mm,光纤孔径角为10°。光纤头固定在光学平台上,可进行上下及左右二维移动。收集光路示意如图2所示。其中,放电区与光纤头分别位于透镜二倍焦距处,透镜焦距f为75 mm,孔径为25.4 mm。

图2 μ-PPT放电区光谱采集系统示意Fig.2 Schematic of OES acquisition system
为了进行此类脉冲等离子体发射光谱的实时测量,需采用CCD光谱仪,以实现等离子体发射光谱的同步瞬时采集。本方案中,光谱仪曝光时间为0.1 ms,保证远大于放电的持续时间(3~20μs),放电发光的持续阶段被光谱仪曝光期完全覆盖。用一个与火花塞点火触发信号同步的5 V TTL信号触发CCD,保证光谱采集与放电周期同步。
为了清晰理解光信号与放电发光区位置的关系,根据以上分析,可将放电区划分为沿等离子体喷出方向堆积的众多矩形发光单元,该单元也可认为是等离子体薄片。图3中所标记的单元为距离推进剂5 mm处的等离子体截面,由于此处截面远离推进剂,位于放电腔室(喷口)中心位置,可作为推力器等离子体发光信号的典型代表。图3为与图2对应的侧视成像示意,其中矩形为推力器等离子体截面示意。凸透镜为理想的薄透镜。根据几何关系,可得

式中:α1、α2为光线经透镜会聚到像点的光线与轴向最大夹角;h为凸透镜半径;x为A点与矩形盘中心的径向距离(0 mm≤x≤12.5 mm);α为A点光线经透镜会聚到像点的光线的最大张角,即α=α1+α2。根据式(4)和式(5)计算可以得到张角与径向距离的关系,如图3(b)所示,从中可得张角与发光点的径向位置无关,数值为定值9.7°。由于光线孔径角为10°,可知所选矩形发光单元中任一发光点经透镜会聚光线都能被光纤端面所收集。如果光纤固定,为保证光源点光线被全部收集,由于光纤直径为1 mm,则x最大取值为1 mm(见图4线段BB1),此时在x范围内的光源发出的光经透镜全部能够被光纤端面所收集。
图4为处于2倍焦距处光纤收集光信号的高效区光路示意,进一步分析了光纤对于发光矩形盘内沿着光轴方向上不同位置发光点的光纤收集效率。首先,考察矩形发光盘中心右侧距离Δr处的发光点,其发出的光经透镜成像与光纤端面前方Δy1处,根据几何关系及透镜成像的高斯公式有

式中:h1为光纤直径(1 mm);Δy2为物距; Δy3为像距;f为焦距。结合式(6)和式(7)可得Δr=Δy3-2f=6.15 mm(见图4线段OC)。同理可得矩形发光单元中心左侧距离Δr为5.68 mm(见图4线段OC1)。
综上,可以得出发光矩形盘内的CC1及BB1线上点光源发出的光能够全部被光纤收集,这也是发射光谱诊断中光信号的主要来源。

图3 与图2对应的光收集成像示意Fig.3 Schematic of light lines collected byoptical fiber(Corresponding to Fig.2)

图4 处于二倍焦距处光纤收集轴向光信号的高效区光路示意Fig.4 Schematic of light lines collected by optical fiber located at two focal lengths
2.2 光谱仪的传递函数测量
在针对试验光谱数据进行数据处理之前,首先针对CCD光谱仪的仪器传递函数进行试验测定。方法如下:利用一台商用小功率(3 m W)氦氖激光器单横模输出状态,发出波长为632.8 nm的激光束,照射在平面毛玻璃表面上,谱仪光纤以法线方向一定角的方向收集散射光,光谱仪记录散射光的谱图。根据激光器的标称指标:激光束的自然线宽为0.000 4 nm,相对于光谱仪的分辨率而言,此激光可以视为单色光源,测得的谱线线型就可以视为谱仪的传递函数,即谱仪加宽。
3 数据处理及误差分析
3.1 数据处理
基于以上分析,在本方案设计中,进行谱线线型分析只需要考虑Stark加宽、多普勒加宽和仪器加宽即可。其中多普勒加宽氢原子热运动,只要能够测得放电通道的热力学温度,多普勒加宽即可计算得到。Hα、Hβ谱线线型是由Lorentz(Stark)和高斯(多普勒、仪器展宽)线型卷积成的佛克脱线型决定的。Stark效应引起的谱线加宽可以通过从总的谱线线型中去卷积分离除去线型中的高斯成分而得到。标准高斯线型为
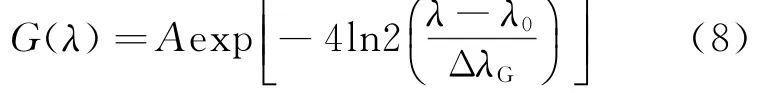
式中:A为归一化常数;ΔλG为高斯加宽全宽,根据误差函数的性质

可以写成最终高斯线型的表达式:
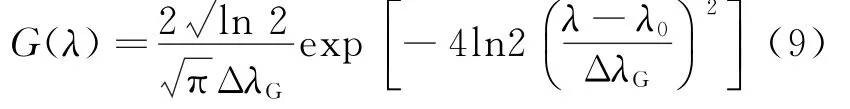
洛仑兹线型可以表达为
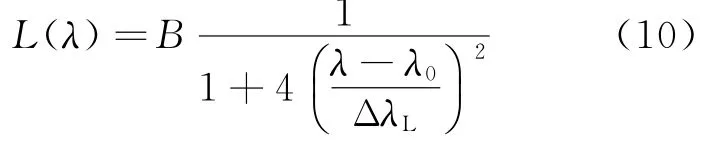
对于高斯和Lorentz线型卷积形成的佛克脱线型

最终,可以得到
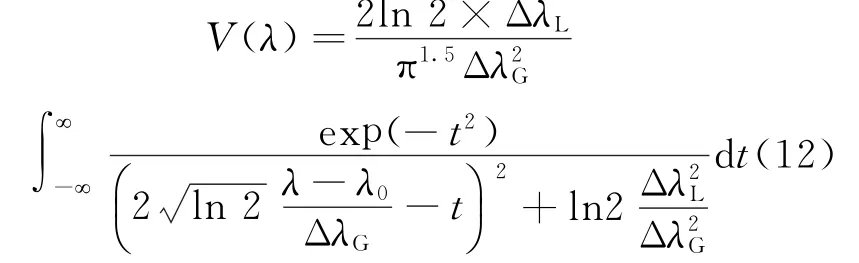
式(12)存在两个常数ΔλG和ΔλL,只要借助于谱线线型拟合方法,获得谱线中的两种成分的半高全宽,就可以得到Δλstark。根据本试验技术方案研究的对象等离子体的特征参数,估计对应的Δλstark值,应该落在0~0.05 nm范围内,所以在编程拟合光谱线型时,设定Δλstark在0.05 nm范围内以步长0.002 nm逐渐增大。每变化一个Δλstark值,就可以从理论上给出一条谱线线型轮廓,把理论线型和试验线型相比较,当它们符合最好时,对应的Δλstark就可以用于计算电子密度。
3.2 误差分析
利用Stark加宽方法计算电子密度的准确性,按文献[17]的分类,氢谱线的使用属于A类,相应的线型理论计算确定度为10%(W1)以内。除此之外,试验数据以及拟合过程的误差,也是影响最终结果准确性的因素。试验数据的准确性主要取决于数据的信噪比和重复性。可通过分析光谱相对强度获得信噪比(在W2以内)。而重复性则可以由于采用了10次测量平均的方案,来判断是否完全重复。拟合过程的误差来源于拟合模型的合理性,以及拟合计算结构的符合程度。可根据不同标准光源(如标准汞灯光源)两条谱线的线宽之差的测量结果的重复程度,可以认为对于Stark加宽宽度拟合计算的误差范围在(波长宽度拟合精度)/(平均Stark加宽度)=W3以内。将上述分析误差累加(W1+W2+W3),可获得电子密度的计算误差。需指出的是,考虑到电子密度的测量主要是数量级的判定,即使误差数值范围很大(低于100%),仍然是可信的。
3.3 加入氢气对PPT等离子体放电的干扰
基于H原子谱线Stark加宽诊断PPT的电子密度需要引入氢气作为探测气体。在PPT放电空间引入氢气,带来两个方面的干扰。一是氢气混入PPT放电通道,成为等离子体的杂质气体,影响放电通道的击穿特性和增长特性。二是加入氢气后,放电空间背景气压会提高,可影响放电产生的等离子体羽流的扩散。研究表明,加入足够多的氢气,其影响体现在等离子体电子密度增加以及等离子体温度的改变。其中温度变化是由于氢气与其他放电气体成分具有不同的热导率。Preston等[18]的研究表明,等离子体温度较低时,加氢气主要影响电子密度,并指出电子密度测量修正可采用基于Saha方程修正的方法。这也就是在局部热力学平衡的条件下,获得加氢气后等离子体的温度变化ΔT,通过Saha方程求出对应的电子密度变化Δn,从而完成对电子密度值的修正。
对于本文讨论的PPT等离子体放电,其本质上是脉冲真空弧放电,放电通道上由于固体推进剂表面的瞬间高温烧蚀形成了局部高压高温气体,使得强大放电电流得以持续。由此,放电电流持续期间,放电通道气压远高于背景真空气压,即使加氢气使背景真空度由10-3Pa升高至10-2Pa水平,真空背景气体对放电通道气压和成分的改变也可以忽略,因此不会影响放电通道的放电特性。脉冲阴极弧物理过程的大量研究表明[19]:在背景真空度为10-3~10-2Pa时,脉冲弧都能形成定向喷射的等离子体束流。综上所述可知:即使将背景真空度由于加氢气由10-3Pa升高至10-2Pa水平,真空弧放电仍然可以不受影响,形成的等离子体羽流的形态也基本不发生变化,所以只要加氢气量限制在真空度不高于10-2Pa水平,就不会对羽流形成有明显影响。
3.4 氢气加入量的选择
PPT放电形成的瞬间等离子体属于真空脉冲电弧等离子体[19],具有高温高密度的特点,处于局部热平衡态。根据真空弧放电的大量研究结果,弧通道中的局部瞬时气体温度可达10 000 K以上。假设加氢气至10-2Pa,以下将对氢原子谱线的辐射强度进行估算。根据理想气体状态方程,可以计算放电前氢分子的数密度N:式中:p为氢气气压;k为玻尔兹曼常数;T为室温温度。

如果加氢气压为10-2Pa,得到氢分子数密度为2.5×1018m-3。放电发生时,气体温度迅速可达104K以上,可以认为氢分子在放电通道上被就地全部解离,H原子数密度5×1018m-3。Hα线n=3的激发态跃迁到n=2的辐射,而上激发态的布居过程是如下电子碰撞过程的结果,可据此估算激发态布居数密度:

对于PPT放电通道,其电子密度一般为1014cm-3量级,因此,处于n=3的激发态布居速率可以如下计算,[H][e]kHdir=5×1012×1014×1.2×10-115cm-3s-1=6×1015cm-3s-1。表1给出了几种不同电子温度下电子碰撞激发产生n=3的激发态的速率常数。

表1 产生激发态H(n=3)的电子激发速率常数[20]Table 1 Electron-impact excitation rate constant to generate excited H atoms atn=3[20]
如果放电通道的等离子体体积按照1 cm3计算,那么放电通道内产生Hα光子的速率为1015~1016s-1,即发光功率可达0.1~1 m W量级。对于常用的光谱光电探测器(PMT或者ICCD)而言,测量这样的发光功率是极容易完成的。
由以上分析估计可知,只要加氢至10-2Pa以下,即可保证对PPT放电过程的干扰微乎其微,又可以容易实现Hα谱线的高信噪比测量,从而完成电子密度的计算。
4 结束语
本文阐述了μ-PPT等离子体电子密度氢原子Stark加宽诊断技术。通过技术方案的设计分析,表明该技术能够适用于μ-PPT等离子体电子密度的测量,并且使电子密度测量下限降至1013cm-3,可大幅度提高电子密度测量准确性。与此同时,分析了光谱测量光路的成像原理和特点,得出了空间分辨测量发射光谱的技术路线。理论层面获得了收集光路设计的空间分辨能力,一定程度上实现对PPT放电区的空间分辨诊断。此外,文中还对测量误差及加氢对于放电状态和等离子体参数的干扰作了预测分析,以保证加氢后的诊断结果不显著偏离。
参考文献(References)
[1] MOLINA-CABRERA P,HERDRICH G,LAU M,et al.Pulsed plasma thrusters:a worldwide review and long yearned classification[C]∥32nd International Electric Propulsion Conference.Wiesbaden,Germany,2011.
[2] 吴莹,白顺波,王俊彦,等.利用微波诊断等离子体的方法[J].光电子技术,2007,27(1):49-54. WU Y,BAI S B,WANG J Y,et al.The methods of plasma diagnosis by microwave[J].Optoelectronic Technology,2007,27(1):49-54(in Chinese).
[3] MURAOKA K,KONO A.Laser Thomson scattering for low-temperature plasmas[J].J.Phys.D:Appl.Phys., 2011,44(4):043001.
[4] TICHY M,HUBICKA Z,SICHA M,et al.Langmuir probe diagnostics of a plasma jet system[J].Plasma Sources Science and Technology,2009,18(1):014009.
[5] MARKUSIC T E,SPORES R A.Spectroscopic emission measurements of a pulsed plasma thruster plume[C]∥33rd Joint Propulsion Conference and Exhibit.Seattle, WA,USA.American Institute of Aeronautics and Astronautics,1997.
[6] BURTON R L,TURCHI P J.Pulsed plasma thruster[J]. J.Propul.Power,1998,14(5):716-735.
[7] TORRES J,PALOMARES J M,SOLA A,et al.A Stark broadening method to determine simultaneously the electron temperature and density in high-pressure microwave plasmas[J].J.Phys.D:Appl.Phys.,2007, 40(19):5929-5936.
[8] TORRES J,JONKERS J,SANDE M J,et al.An easy way to determine simultaneously the electron density and temperature in high-pressure plasmas by using Stark broadening[J].J.Phys.D:Appl.Phys., 2003,36(13):L55-L59.
[9] QIAN M Y,REN C S,WANG D Z,et al.Stark broadening measurement of the electron density in an atmospheric pressure argon plasma jet with doublepower electrodes[J].Journal of Applied Physics, 2010,107:063303.
[10] SCHÖBHERR T,NEES F,ARAKAWA Y,et al. Characteristics of plasma properties in an ablative pulsed plasma thruster[J].Physics of Plasma, 2013,20:033503.
[11] LIU F,NIE Z F,XU X,et al.Measurement of electron density by Stark broadening in an ablative pulsed plasma thruster[J].Applies Physics Letters, 2008,93:111502.
[12] SANSONETTI J E,MARTIN W C.Handbook of basic atomic spectroscopic data[J].J.Phys.Chem.Ref.Data, 2005,34(4):1763-1764.
[13] GRIEM H R.Spectral line broadening by plasmas[M]. New York:Academic Press,1974:226.
[14] GRIEM H R.Principles of plasma spectroscopy[M]. Cambridge:Cambridge University Press,1997:226.
[15] OVSYANNIKOV A A,ZHUKOV M F.Plasma diagnostics[M].Cambridge:Cambridge International Science,2000:24.
[16] WAGNER H P,AUWETER-KURTZ M.Slug model and snowplow model for pulsed plasma thruster description[C]∥40th AIAA/ASME/SAE/ASEE Joint Conference an Exhibit.Fort Lauderdale,Florida,2004: 3466.
[17] KONJEVIC N,WIES W L.Experimental Stark widths and shifts for spectral lines of neutral atoms[J].J.Phys Chem.Ref.Data,1984,13:619.
[18] PRESTON R C.Spectroscopic studies of a plasma temperature and radiation standard based on a wallstabilized ARC[J].J.Quant.Spectrosc.Radiat. Transfer,1977,18:337-360.
[19] ANDERS A,YUSHKOV G Y.Ion flux from vacuum arc cathode spots in the absence and presence of a magnetic field[J].J.Appl.Phys.,2002,91(8):4824-4832.
[20] GENG Z C,XU Y,YANG X F,et al.Atomic hydrogen determination in medium-pressure microwave discharge hydrogen plasmas via emission actinometry[J]. Plasma Sources Sci.Technol,2005,14:76-82.
(编辑:高珍)
A diagnostic scheme for electron density inμ-PPT plasma using H Stark broadening
WANG Shangmin1,ZHANG Jialiang2,*,ZHANG Tianping1,FENG Jie1,ZHENG Maofan1, HUANG Yongjie1
1.Lanzhou institute of Physics,Lanzhou 730000,China 2.Dalian University of Technology,Dalian 116024,China
A method of electron density measurement inside discharge channel of pulsed-plasma thruster(PPT)with higher accuracy was proposed,based on Stark broadening spectrum analysis.By measuring the line profile and the full-width at half-maximum(FWHM)of C atom spectrum emitted by PPT plasma,the electron density can be calculated.But this requires adequate high electron density.If the electron density is lower than 1016cm-3,the accuracy of diagnosis is dramatically decreased.Therefore,a tiny H tracer based on H atom spectrum of the line profile and the full-width at halfmaximum was proposed to measure the electron density.Comparing with the conventional method,it can improve remarkably the accuracy of electron density measurement.
electron density;Stark broadening;analysis of H atom spectrum;pulsed-plasmathruster;high-precision measurement
V439+.2/4
:A
10.3780/j.issn.1000-758X.2016.0016
2015-11-12;
:2015-12-10;录用日期:2016-01-18;< class="emphasis_bold">网络出版时间
时间:2016-02-24 13:34:07
http:∥www.cnki.net/kcms/detail/11.1859.V.20160224.1334.006.html
兰州空间技术物理研究所自主研发项目(YSC0714)
王尚民(1986-),男,工程师,wangshangmin2008@163.com
*通讯作者:张家良(1967-)男,教授,zhangjl@dlut.edu.cn,主要研究方向为电推进等离子体诊断
王尚民,张家良,张天平,等.μ-PPT等离子体电子密度氢光谱诊断技术[J].中国空间科学技术,2016,36(1):
94-102.WANG S M,ZHANG J L,ZHANG T P,et al.A diagnostic scheme for electron density inμ-PPT plasma using H Stark broadening[J].Chinese Space Science and Technology,2016,36(1):94-102(in Chinese).
http:∥zgkj.cast.cn

