放电电压和屏栅电压对离子推力器性能的影响

王雨玮,任军学,*,吉林桔,汤海滨

1.北京航空航天大学宇航学院,北京100191 2.北京动力机械研究所,北京100074

放电电压和屏栅电压对离子推力器性能的影响

王雨玮1,任军学1,*,吉林桔2,汤海滨1

1.北京航空航天大学宇航学院,北京100191 2.北京动力机械研究所,北京100074

利用试验和数值模拟相结合的方法研究6 cm Kaufman离子推力器放电电压和屏栅电压的变化对其工作性能的影响。试验中,离子推力器使用氩气作为推进剂,测量了多组不同工况下的性能参数。此外,基于Goebel的理论模型模拟了放电电压对束流电流和推进剂利用率的影响;采用单元内粒子-蒙特卡罗碰撞(PIC-MCC)方法模拟屏栅电压对束流电流、推进剂利用率和加速栅极电流的影响。试验和数值模拟结果一致,发现当放电电压逐渐增大时,引出的束流电流和推进剂利用率先增加然后趋于稳定;当屏栅电压逐渐增大时,引出的束流电流和推进剂利用率先增加然后趋于稳定,加速栅极电流先减小后趋于稳定。研究可以为提高多模式离子推力器的性能提供参考。

离子推力器;多模式;放电电压;屏栅电压;氩气

离子推力器具有比冲高、效率高、工作时间长和安全环保等特点,在空间任务中应用广泛。近年来,随着离子推力器的应用逐渐由传统的地球静止轨道任务向深空探测和中低轨道高精度姿态控制等多元化任务发展,推力器在完成主推进任务的同时,有时还要兼顾航天器轨道保持和姿态控制的要求[1-3]。这就需要离子推力器可以在多模式下工作。目前,国外已经成功研制了多种多模式离子推力器。例如应用于DS-1航天器和DAWN航天器的30 cm NSTAR离子推力器,单台推力器工作功率为0.49～2.31 k W,比冲为19 500～32 800 m/s,推力为19.5～92 m N,效率为38%～64%,共有5种推力模式[4-6]。XIPS-25推力器主要有2种工作模式,功率、比冲、推力、效率分别为4.5 k W、3.0 k W,35 000 m/s、34 000 m/s, 165 m N、79 m N,65%、63%[7]。NEXT推力器主要有2种工作模式,功率、比冲、推力、效率分别为6.9 k W、2.5 k W,41 900 m/s、40 000m/s,237 m N、80.4 m N,71%、64%[8]。

多模式离子推力器主要通过调节推力、比冲和效率来满足不同任务的要求。加州理工大学的Goebel和Katz[9]及兰州空间技术物理研究所的郑茂繁和江豪成[10]认为在不考虑束流发散和双荷离子影响的情况下,推力和比冲的大小可以由束流大小反映;比冲的大小由屏栅电压决定;利用束流电流、放电电压和屏栅电压可以计算放电损耗从而确定推力器的电效率。但是他们没有从放电室的工作原理出发完整解释放电电压和屏栅电压对束流电流的具体影响。北京航空航天大学的仇钎[11]、任军学等[12-13]对屏栅的工作过程和束流的引出情况也进行了仿真研究。但是他们的研究仅限于对单个栅极孔的分析,没有得到屏栅电压与总的束流电流和总的加速栅极电流之间的关系曲线,也没有进行相关试验对结论进行验证。

因此,本文首先从放电室微观工作过程出发,模拟分析6 cm Kaufman离子推力器放电电压的变化对束流电流和推进剂利用率的影响;屏栅电压对束流电流、推进剂利用率和加速栅极电流的影响。然后,进行相关试验对分析结果进行验证,得到参数之间的宏观关系曲线。本文的研究可以为多模式离子推力器性能的提高和参数优化设计提供参考,促进其在工程上的应用。

1 试验系统介绍

1.1 Kaufman离子推力器

典型的Kaufman离子推力器主要由主阴极、放电室、光学系统和中和阴极4部分组成。其工作原理是主阴极发射电子与放电室内的中性气体原子碰撞,使其电离产生离子;然后,屏栅极和加速栅极组成的光学系统将离子从放电室引出并利用栅极间的电压将其加速喷出;最后中和阴极发射电子中和引出的离子束,使离开推力器的粒子束保持电中性。典型的离子推力器结构如图1[14]所示。

本次研究使用6 cm Kaufman离子推力器,为便于试验操作,离子推力器的主阴极和中和阴极都使用直热式钨丝。主阴极灯丝位于放电室中央,采用双阴极(一个阴极工作,另一个备用),可不开真空罐切换阴极,能增加离子推力器的连续工作时间。放电室的结构参数见表1。

光学引出系统采用双栅极,屏栅极和加速栅极的孔径和厚度都相等,都使用平面栅。栅极的结构参数如表2所示。

图1 Kaufman离子推力器的结构[14]Fig.1 Structure of Kaufman ion thruster

表1 放电室的结构参数Table 1 Structure parameters of discharge chamber

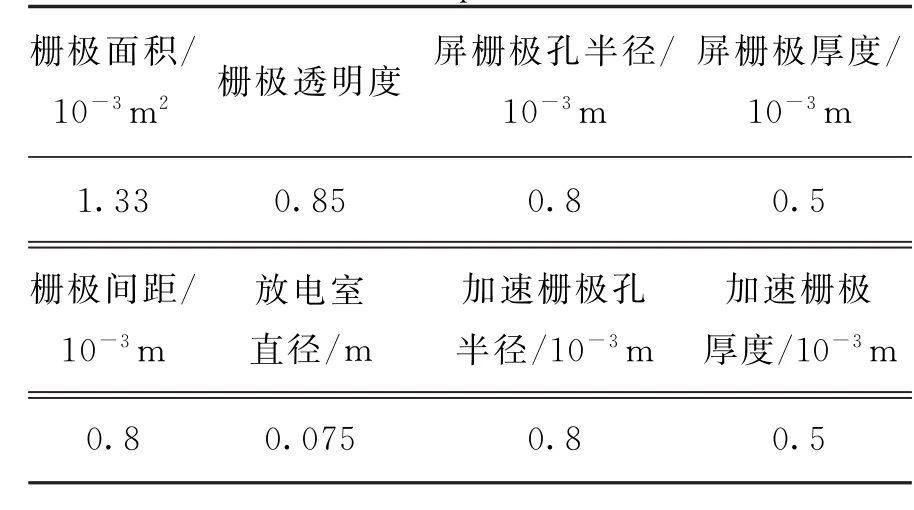
表2 栅极结构参数Table 2 Structure parameters of screens

1.2 推进剂储供系统

推进剂供给系统由气瓶、压力表、减压阀、管路及质量流量控制器等组成。试验采用氩气作为推进剂。使用S49 32/MT气体质量流量控制器,它使用氮气标定,本次试验使用的量程为5～500 m L/min。流量控制器的工作压差范围为50～300 k Pa,重复精度为±0.2%F.S。

1.3 真空系统

高空模拟真空系统主要包括模拟舱,真空泵和控制系统三个部分。真空舱的直径为1.8 m。系统有三级泵,包括2台高真空油扩散泵,2台罗茨泵和4台机械泵。离子推力器点火前真空舱的本体压力为4.7×10-3Pa,试验时模拟舱中的压强不高于1.2×10-2Pa。

2 放电电压对束流电流和推进剂利用率的影响

2.1 理论计算方法

Goebel在2006年提出的会切磁场零维等离子体放电室模型得到了离子推力器放电损耗与推进剂利用率之间的关系曲线。本节将基于Goebel的理论分析束流电流和推进剂利用率随放电电压的变化情况。由于各个参数之间相互耦合,无法直接解出束流电流和推进剂利用率随放电电压变化的关系式。因此,首先根据放电室内中性气体密度守恒和放电电流守恒求解出每个特定的放电电压对应的束流电流和推进剂利用率的值。然后在2.2节中将其拟合,得到束流电流和推进剂利用率随放电电压变化的关系曲线。

(1)中性气体密度守恒公式

根据离开放电室的中性气体的流量Qout(未被电离的工质)等于进入放电室的气体流量Qin减去被电离并引出的离子束的气体流量:

式中:Ib为引出的束流电流。离开放电室的中性气体的流量为

式中:n0为放电室内中性气体的密度;v0为中性原子速度;As为栅极面积;Ts为栅极透明度;ηc为克劳辛系数。推进剂利用率ηm指的是产生单位束流电流需要消耗的推进剂,是衡量放电室性能的关键参数,其定义为

联立式(1)～式(3)可以得到中性气体密度的表达式为

此外,中性气体的密度还可以由离子平衡方程得到,对于一个未磁化的等离子体来说,任意方向流出等离子体的电流Ii可以由波姆电流得到:

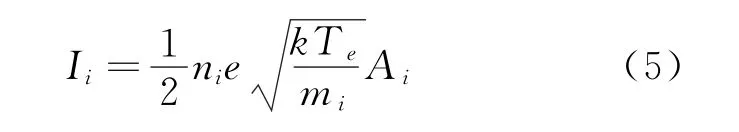
式中:ni为放电室内离子的密度,约等于二次电子的密度ne;k为玻尔兹曼常数;Te为电子温度;mi为氩原子的质量;Ai为所有离子吸收面积之和。电离室内的离子由阴极发射的原初电子以及二次电子电离气体产生,单位时间内产生的离子数量Ip为

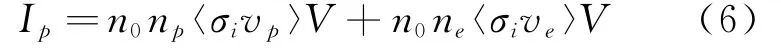
式中:np为原初电子密度;vp为原初电子速度;ve为二次电子的速度;σi为电离截面积;V为放电室的体积;〈σivp〉为原初电子的反应速率;〈σive〉为二次电子的反应速率。总的离子产生速率等于总的离子吸收率:

联立式(5)～式(7)可以得到:

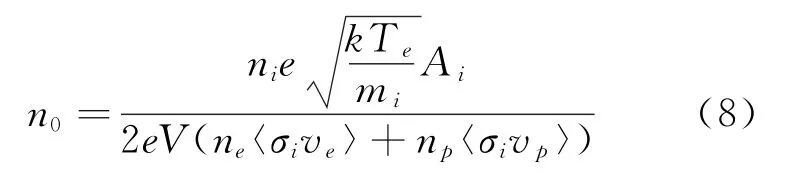
联立式(4)和式(8)可以得到中性气体密度的守恒公式:

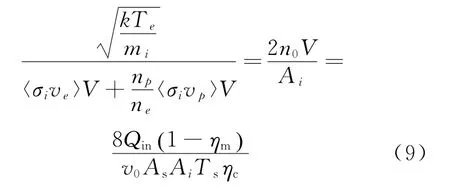
(2)放电电流守恒公式

首先,根据放电室内输入功率与输出功率的守恒推导出与电子温度和束流电流相关的放电损耗的表达式,具体过程如下。

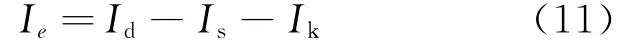
求流动到阳极的二次电子电流Ia:式中:Id为放电电流;Iia为到达阳极的离子电流;IL为原初电子电流。阴极发射的电流Ie为式中:Is为屏栅极电流;Ik为返回到阴极的离子电流。输入放电室的功率Pin等于阴极发射电流乘以电子在电离室内截获的电压Vk:

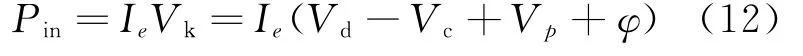
式中:Vd为放电电压;Vc为阴极电压;Vp为等离子体区电势;φ为相对于阳极壁面的鞘层电势。放电室消耗的功率Pout用于引出从阴极发射的原初电子以产生离子、激发态中性粒子和二次电子。离开放电室到达电极的能量主要包括离子向阳极、阴极和屏栅极的输运,以及原初电子和二次电子与阳极的碰撞。输出功率等于以上各项之和,具体表达式为

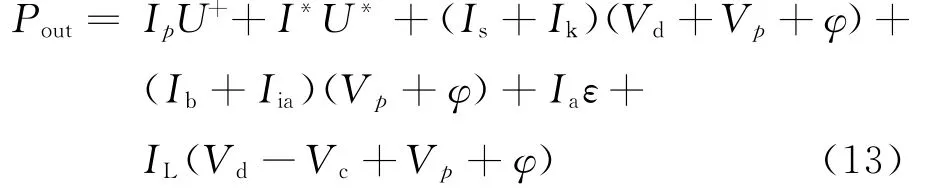
式中:U+为气体电离势能;I*为激发态离子电流;U*为气体激发势能;TeV为电子温度;ε为二次电子和阳极壁面碰撞损失的能量。根据输入功率等于输出功率,联立式(12)和式(13),同时利用式(10)和式(11)得到:

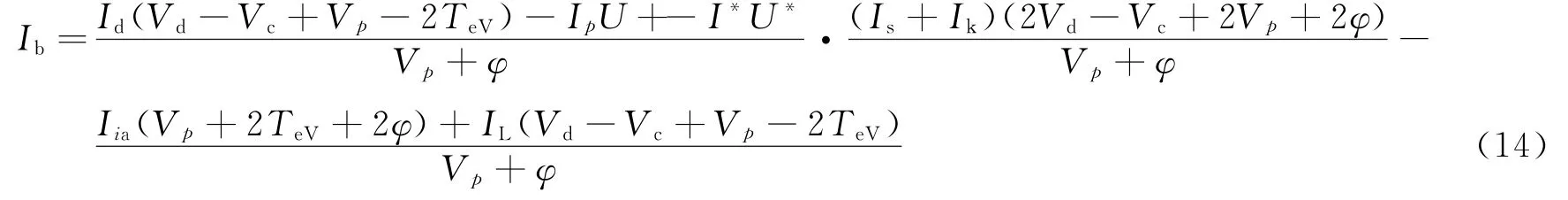
因此,放电损耗εe可以表示为然后,根据离子推力器的工作原理可得,引出的离子束流电流等于到达栅极的离子电流乘以栅极的透明度:

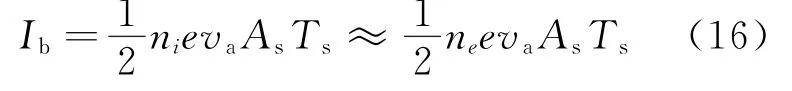
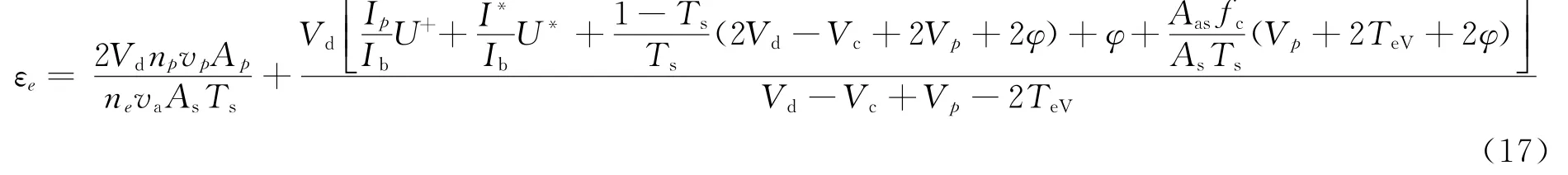
式中:va为离子声速。将式(16)带入式(15)(具体替换以及其他参数的带入过程见文献[9]),得到本节将使用的求解放电损耗公式:式中:Aas为阳极壁面面积;fc为离子声速和玻姆速度之比(Va/Vbohm);Ap为原初电子损失面积,根据式(17)得到放电电流的守恒公式:

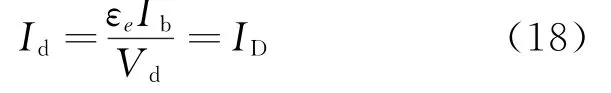
放电电流守恒公式中的Ib由式(3)得到,ID是从试验中读取的放电电流。

(3)特定放电电压对应的放电电流和推进剂利用率求解方法

在放电室结构参数和推力器工况确定的情况下,守恒式(9)和式(18)都只与电子温度和束流电流相关。因此本节联立式(9)和式(18)在每个放电电压下计算都能得到一组电子温度和束流电流的解满足式(9)和式(18)。

2.2 结果与分析

从30 V开始,以2.5 V为间隔,逐渐增加阳极电压,到60 V为止,求解每个特定的放电电压对应的束流电流和推进剂利用率值。求解方法如2.1节所述。对数据进行拟合,得到放电电压对束流电流和推进剂利用率之间的理论变化关系曲线。

同时,利用试验得到每个放电电压下,束流电流和推进剂利用率的值,与理论结果进行比较。试验工况如表3所示。

表3 改变放电电压的试验工况Table 3 Conditions of discharge voltage changed experiments

图2和图3给出了束流电流和推进剂利用率在相应的阳极电压下理论计算和试验结果(放电电压为42.5V时,试验得到的束流电流和推进剂利用率误差较大,因此未予显示)。

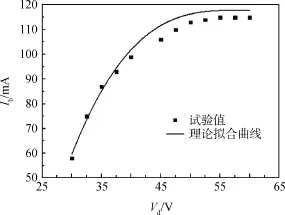
图2 放电电压对束流电流的影响Fig.2 Effect of discharge voltage on beam current

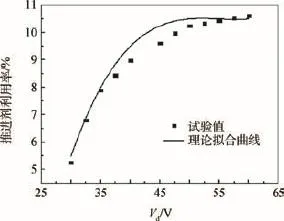
图3 放电电压对推进剂利用率的影响Fig.3 Effect of discharge voltage on propellant utilization efficiency

由图2和图3可以看出,在30～60 V区间内,随着放电电压的增加,引出的束流电流和推进剂利用率先增加然后趋于稳定。这是因为推力器工作时,电子是在磁场和电场的共同约束下轰击推进剂中性原子使其电离。只提高放电电压时,电场强度随之增加,使得电磁场对电子的约束效果增强。与此同时,电场强度增加也提高了电子运动速度,提高了电子的能量,增加了原子的电离率。更多的原子电离会使得放电室内的离子密度增加,到达栅极的离子数会增加,所以其他条件不变的情况下,引出的离子束流电流和推进剂利用率随之增加。

当放电电压为45 V时,理论和试验对应的束流电流大小分别为110 mA和106 mA,推进剂利用率大小分别为10.0%和9.6%。当放电电压大于45 V后,束流电流和推进剂利用率的增速逐渐变缓,然后趋于稳定。放电电压过高,会产生大量双核离子,导致离子的生成成本增加。此外,计算原初电子损失面积的表达式为[9]

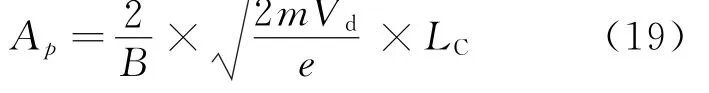
式中:B为环尖处磁场强度;m为电子质量;LC为磁尖总长。从式(19)也可以发现当放电电压增加时,磁尖处原初电子的损失面积增大,直接损失的原初电子增加,会影响电离率,使束流电流和推进剂利用率的增速减慢。

3 屏栅电压对束流电流、推进剂利用率和加速栅极电流的影响

3.1 理论计算方法

采用单元内粒子-蒙特卡罗碰撞(PICMCC)方法,模拟束流离子及CEX离子在栅极间的分布情况,可以得到在其他条件不变的情况下,每个特定屏栅电压对应的单个小孔的束流电流、加速栅极电流、离子的运动轨迹和分布情况。计算过程中,认为电子是符合玻尔兹曼分布,采用的粒子比例是1 000,计算8 000步后,离子数稳定。计算区域和等离子体参数的选择见文献[12]。

此外,总的束流电流和总的加速栅极电流由上述单个小孔的电流乘以小孔数量得到。推进剂利用率利用式(3)计算得到。

3.2 结果与分析

从300 V开始,以50 V为间隔,逐渐增加屏栅电压,到600 V为止。首先根据3.1节的方法计算得到各个屏栅电压对应的束流电流和加速栅极电流的值。然后根据式(3)计算每个束流电流对应的推进剂利用率。将得到的束流电流、推进剂利用率和加速栅极电流值进行拟合,得到它们与屏栅电压之间的关系曲线。同时,利用试验得到每个屏栅电压下,束流电流和推进剂利用率的值,与理论结果进行比较。试验工况如表4所示。

表4 改变栅极电压的试验工况Table 4 Condition of screen grid voltage changed experiments

图4和图5给出了束流电流和推进剂利用率在相应的屏栅电压下理论计算和试验结果。图6为加速栅极电流随屏栅电压变化的试验结果和理论结果。

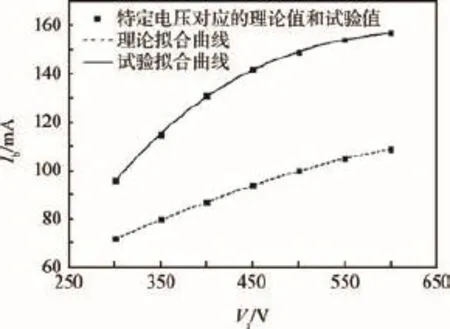
图4 屏栅电压对束流电流的影响Fig.4 Effect of screen grid voltage on beam current

图5 屏栅电压对推进剂利用率的影响Fig.5 Effect of screen grid voltage on propellant utilization efficiency

从以上4幅图可以看出,随着屏栅电压的增加,引出的束流电流和推进剂利用率先增加然后趋于稳定,加速栅极电流先减小后趋于稳定。这种现象主要是导流系数变化引起的[15]。

在其他影响参数(栅极结构、放电室等离子体密度、加速栅极电压等)确定的情况下,屏栅电压决定导流系数的大小。利用3.1节的方法,计算屏栅电压为300 V、450 V和600 V三个工况下单个孔离子数量分布情况,分析在300～600 V范围内屏栅电压对导流系数的影响,如图7所示。

从图7可以得到,屏栅电压从300～600 V变化时,随着屏栅电压的增加,导流系数不断减小,放电等离子体鞘层弧度增加,离子束的入射角度发生变化,被聚焦程度越来越大。

因此,当栅极电压为300 V时,导流系数过大,很多离子直接轰击在加速栅极上游表面,导致引出的束流电流较小,加速栅极电流较大,产生溅射,影响栅极寿命。随着屏栅电压的增大,导流系数逐渐减小,束流电流和推进剂利用率随之增加,加速栅极电流随之减小。从图4～图6综合来看,离子推力器使用氩气作推进剂时,在本节试验工况下,最佳导流系数大概出现在550 V附近。当屏栅电压超过550 V后,随着栅极电压的升高,导流系数变得过小,束流被过度聚焦,在栅极孔内发生交叉,离子会轰击加速栅极孔内壁和表面,增加损耗。因此束流电流的增速逐渐减小,电流值逐渐趋于稳定;加速栅极电流减少的速率也变慢,电流值逐渐趋于稳定。

此外,图6中加速栅极电流的试验数据要比理论数据值高。将图6与NSTAR-30离子推力器在功率2.3 k W、推力92.7 m N,比冲31 270 m/s、效率61.8%工况下模拟得到的加速栅极电流随屏栅电压的理论变化情况(如图8[9]所示)对比,可以得到图7的理论数据可靠性较高。

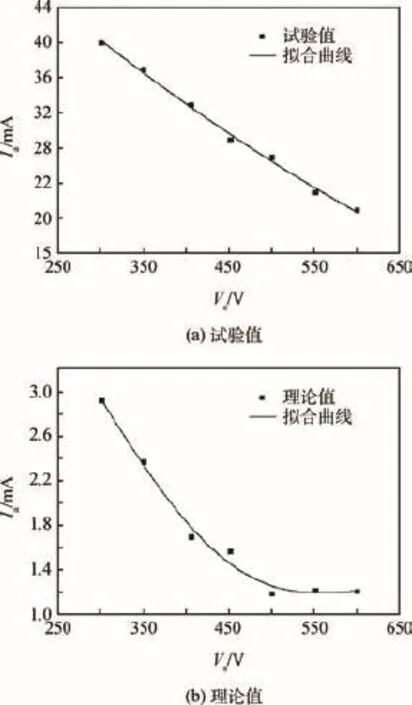
图6 加速栅极电流随屏栅电压变化的试验结果和理论结果Fig.6 Experiment and theory result of acceleration grid electric current’s changing with screen grid voltage

图7 屏栅电压为300 V、450 V和600 V时离子数量分布Fig.7 Distribution of ion numbers at the screen grid voltage of 300 V,450 V and 600 V

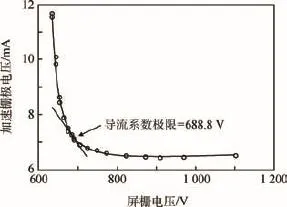
图8 NSTAR-30推力器加速栅极电流随屏栅电压的变化Fig.8 Changing of accelerating grid current with screen grid voltage’s changing of NSTAR-30 thruster

而造成试验中加速栅极电流过高的原因主要有两个:一是本次试验使用的推力器是用于高校教学研究的产品,推力器的加工工艺有局限性,尤其是屏栅极和加速栅极的平行度、小孔的对准精度不够高,会导致加速栅极电流增加;二是试验过程中,屏栅极和加速栅极的热变形以及点火后真空舱内真空度的提高也会造成的加速栅极电流的增加。

4 结束语

本文通过试验和理论模型相结合的方法,分析了6 cm Kaufman离子推力器在使用氩气作为推进剂时,放电电压对束流电流、推进剂利用率的影响;以及屏栅电压对束流电流、推进剂利用率、加速栅极电流和导流系数的影响,并给出了参数之间宏观的变化关系曲线。理论模拟和试验结果相符合,结论如下:

1)只改变放电电压时,随着电压的增加,引出的束流电流和推进剂利用率先增加然后趋于稳定。

2)只改变屏栅电压时,随着屏栅电压的增加,导流系数不断减小,离子束被聚焦的程度越来越高;引出的束流电流和推进剂利用率先增加,到达最佳导流系数状态后趋于稳定;加速栅极电流逐渐下降,到达最佳导流系数状态后趋于稳定。对于多模式的离子推力器,设定工作模式时,应尽量避免使用过高的放电电压,减少双核离子的产生电功率的损失;而且应尽量使推力器工作在最佳导流系数状态附近。

References)

[1] 郑茂繁,耿海,梁凯,等.用于小行星探测的离子推力器技术研究[J].深空探测学报,2015,2(3):236-240. ZHENG M F,GENG H,LIANG K,et al.Research on ion thruster technology for asteroid exploration[J]. Journal of Deep Space Exploration,2015,2(3):236-240(in Chinese).

[2] 温正,王敏,仲小清.多任务模式电推进技术[J].航天器工程,2014,23(1):118-123. WEN Z,WANG M,ZHONG X Q.Multitask mode electric propulsion technologies[J].Space Engineering, 2014,23(1):118-123(in Chinese).

[3] OH D Y,SANTIAGO G.Analytic optimization of mixed chemical-electric orbit raising missions[C]∥Proceedings of the 26th International Electric Propulsion Conference,2001.

[4] RAWLIN V K,SOVEY J S,HAMLEY J A.An ion propulsion system for NASA’s deep space missions, AIAA-1999-4612[R].Reston:AIAA,1999.

[5] CARDELL G,UILOA-SEVERINO A,GROSS M.The design and operation of the DAWN power system, AIAA-2012-3898[R].Reston:AIAA,2012.

[6] BROPHY J R,MARCUCCI M G,GANAPATHI C B,et al.The ion propulsion system for DAWN, AIAA-2003-4542[R].Reston:AIAA,2003.

[7] GOEBEL D M,MARTINEZ-LAVIN M,BOND T A,et al.Performance of XIPS electric propulsion in on-orbit station keeping of the Boeing 702 spacecraft, AIAA-2002-4348[R].Reston:AIAA,2002.

[8] HERMAN D A,SOULAS G C,PATTERSON M J. Performance evaluation of the prototype model NEXT ion thruster,AIAA-2007-5212[R].Reston:AIAA, 2007.

[9] GOEBEL D M,KATZ I.Fundamentals of electric propulsion:ion and hall thrusters[M].New Jersey: John Wiley&Sons Inc,2008:91-232.

[10] 郑茂繁,江豪成.离子推力性能评价方法[J].真空与低温,2012,18(4):223-227. ZHENG M F,JIANG H C.Method of performance evaluation for ion thruster[J].Vacuum&Cryogenics, 2012,18(4):223-227(in Chinese).

[11] 仇钎.离子发动机交换电荷离子分布的数值模拟[D].北京:北京航空航天大学,2010. QIU Q.Numerical simulation of charge-exchange propagation in the plume of ion thruster[D].Beijing: Beihang University,2010(in Chinese).

[12] 任军学,谢侃,汤海滨,等.离子发动机加速栅极孔扩大腐蚀的粒子模拟[J].推进技术,2013,34(10): 1432-1440. REN J X,XIE K,TANG H B,et al.Particle simulation of the acceleration grid aperture erosion in ion thruster[J].Journal of Propulsion Technology, 2013,34(10):1432-1440(in Chinese).

[13] 任军学,顾左,郭宁,等.离子发动机羽流特征的数值模拟[J].航空动力学报,2013,28(6):1372-1378. REN J X,GU Z,GUO N,et al.Numerical simulation of characteristics of ion thruster plume[J]. Journal of Aerospace Power,2013,28(6):1372-1378(in Chinese).

[14] WIRZ R E.Discharge plasma process of ring-cusp ion thrusters[D].Pasadena:California Institute of Technology,2005.

[15] 于达仁,刘辉,丁永杰,等.空间电推进原理[M].哈尔滨:哈尔滨工业大学出版社,2012:166-167. YU D R,LIU H,DING Y J,et al.Fundamentals of space electric propulsion[M].Harbin:Harbin Institute of Technology Press,2012:166-167(in Chinese).

(编辑:范真真)

Effects of discharge voltage and screen grid voltage on performance of ion thruster

WANG Yuwei1,REN Junxue1,*,JI Linju2,TANG Haibin1
1
.School of Astronautics,Beihang University,Beijing 100191,China 2.Beijing Power Machinery Institute,Beijing 100074,China

The effects of discharge voltage and screen grid voltage changing to working performance of a 6 cm Kaufman ion thruster were studied by combination of experiments and numerical simulation.In these experiments,the argon was used as propellant for the ion thruster,and many groups of data were gathered.Furthermore,based on Goebel's theory model,the effects of discharge voltage changing on beam current and propellant efficiency were simulated.And the particle in cell Monte-Carlo collide(PIC-MCC)theory was used tosimulate the effects of screen voltage on beam current,propellant efficiency and acceleration grid current.Experiments and numerical simulation drew the same conclusions.When discharge voltage increases,ion beam current and propellant utilization efficiency tend to be stable after a corresponding increase.A similar beam electric current and propellant utilization efficiency changing pattern is observed when the screen grid voltage is increased,but acceleration grid voltage tends to be stable after a corresponding decrease.This study can provide a reference for increasing multi-modes ion thrusters'performance.

ion thruster;multi-modes;discharge voltage;screen grid voltage;argon

V439+.1

:A

10.3780/j.issn.1000-758X.2016.0014

2015-11-12;

:2015-12-10;录用日期:2015-12-30;< class="emphasis_bold">网络出版时间

时间:2016-02-24 13:31:27

http:∥www.cnki.net/kcms/detail/11.1859.V.20160224.1331.005.html

北京市高等教育“青年英才”计划(YETP1129)

王雨玮(1992-),男,硕士研究生,412544372@qq.com

*通讯作者:任军学(1980-),男,副教授,rjx_buaa@163.com,主要研究方向为火箭发动机及空间电推进

王雨玮,任军学,吉林桔,等.放电电压和屏栅电压对离子推力器性能的影响[J].中国空间科学技术,2016,36(1):77-84.WANG Y W,REN J X,JI L J,et al.Effects of discharge voltage and screen grid voltage on performance of ion thruster[J].Chinese Space Science and Technology,2016,36(1):77-84(in Chinese).

http:∥zgkj.cast.cn