基于元胞自动机的高速公路临时瓶颈交通流仿真

江欣国， 夏 亮

（1．西南交通大学交通运输与物流学院，四川成都610031；2．综合交通运输智能化国家地方联合工程实验室，四川成都610031）

基于元胞自动机的高速公路临时瓶颈交通流仿真

江欣国1，2， 夏 亮1，2

（1．西南交通大学交通运输与物流学院，四川成都610031；2．综合交通运输智能化国家地方联合工程实验室，四川成都610031）

为研究强制换道及冲突点分布对高速公路临时瓶颈交通流的影响，在NS（NaSch）模型和STCA（symmetric two-lane cellular automata）模型的基础上，引入强制换道规则，根据瓶颈口上游驾驶员心理状态的变化，建立高速公路瓶颈交通流模型．在开口边界条件下，针对不同的安全换道概率、强制换道概率、冲突点距离和冲突区间长度参数，模拟得到瓶颈交通流量和换道频率与车辆到达率的关系．仿真结果表明，安全换道行为对系统流量影响小；强制换道行为是降低瓶颈系统最大流量的主要因素，当安全换道概率为0．5时，强制换道概率从0．0增加至0．1，最大流量下降了17%；冲突点距离的增加缓解了交通拥堵程度，当冲突点距离从1 cell增加至4 cell时，临界车辆到达率上升了4%；冲突区间长度对交通事故风险的影响较大，最大强制换道频率随冲突区间长度的增加而增加．

元胞自动机；瓶颈交通；强制换道；交通冲突

临时交通瓶颈是指由于交通事故或临时作业等临时性事件造成的非常态交通瓶颈．临时交通瓶颈一旦在高速公路出现，将会严重影响高速公路的通行能力．然而，由于临时交通瓶颈具有空间随机性与时间短暂性的特点，使其缺乏相应的交通规划与交通管理措施．为了能够及时应对高速公路上的临时性事件，确保高速公路高能、高效、快速通达的优势，对高速公路临时瓶颈交通流进行全面、系统地分析在我国目前的交通研究中显得尤为重要．

已有许多学者对于临时交通瓶颈对交通流的干扰现象进行了研究［1-4］，其中，数值模拟［1］与仿真分析［2-4］是研究交通流干扰的主要手段．元胞自动机模型（cellular automata，CA）不仅保留了交通这种复杂系统的非线性行为和物理特征，而且还易于计算机操作，并能灵活地修改其模型以考虑各种真实交通条件，这些特点既能解决公式推导繁琐和数据获取困难的问题，又能形象地描述瓶颈交通流的复杂换道行为．文献［5］提出了一种简单的一维单车道元胞自动机交通流（NaSch，NS）模型，之后相继出现了慢启动（Takayasu-Takayuasu，TT）模型［6］、速度效应（velocity effect，VE）模型［7］及Fukui-Ishibashi（FI）模型［8］等．文献［9］又提出了多车道CA模型．许多学者在此基础上提出了改进模型［10-13］，例如对称双车道CA（symmetric two-lane cellular automata，STCA）模型规则［10］．在提出NS模型之后，文献［14］提出了研究网络交通流的二维交通流（Biham-Middleton-Levine，BML）CA模型．

但是以上研究多以理论模型的建立和完善为主，缺少对解决现实问题的应用．也有许多学者利用元胞自动机进行瓶颈交通流研究，例如，文献［1］利用元胞自动机对拥堵传播及消散控制措施进行了仿真分析；文献［15］针对驾驶员在交通拥堵前后行为的变化，建立了考虑交通瓶颈处驾驶特性的元胞自动机模型，并分析了瓶颈现象对驾驶特性的影响；文献［16］探讨了各种意外事件对交通流的影响；文献［17］提出了基于速度的换道规则，并在交通事件中利用改进后的模型和传统的STCA规则进行了对比仿真试验．然而，以上模型仅简单地以速度或距离作为换道行为的判定依据，并未考虑驾驶员在了解车道封闭信息前后的行为差异．

本文综合考虑速度、距离和驾驶员在了解车道封闭信息前后驾驶行为的差异等因素，建立了适应于瓶颈交通流的元胞自动机模型．并以安全换道概率、强制换道概率、冲突点距离和冲突区间长度作为影响因子，对高速公路上单车种且无交通指挥员的瓶颈交通流进行模拟仿真．最后分析了换道概率和冲突点分布对交通瓶颈区流量和交通事故风险的影响，为瓶颈交通流系统的管理提供了理论依据．

1 模 型

交通流CA模型主要将时间、空间以及速度离散化．在该类模型中，道路被离散为若干容纳单位车辆的格子即元胞（cell），并且将元胞宽度定义为车道宽度，元胞长度包括车辆长度和前后安全间距．模型的演化由两大规则组成，分别为直行规则和换道规则．直行规则为车辆个体在保证安全行驶情况下的纵向移动规则；换道规则指车辆个体为追求更高的速度而进行的横向移动规则．改进后模型的直行规则采用NS模型；换道规则由安全换道规则（STCA换道规则）和强制换道规则（cellular automaton model for bottleneck flow，CABF换道规则）组成，其中STCA换道规则优先．

文献［18］中将由公交车停靠诱发的交通瓶颈区域划分为上游远离车站的部分、车站上游影响区域路段、车站和下游非车站的部分．为方便描述高速公路临时交通瓶颈，本文将一条单向双车道瓶颈道路分成瓶颈区、瓶颈口、上游影响区和上游无影响区4个区域，如图1所示．

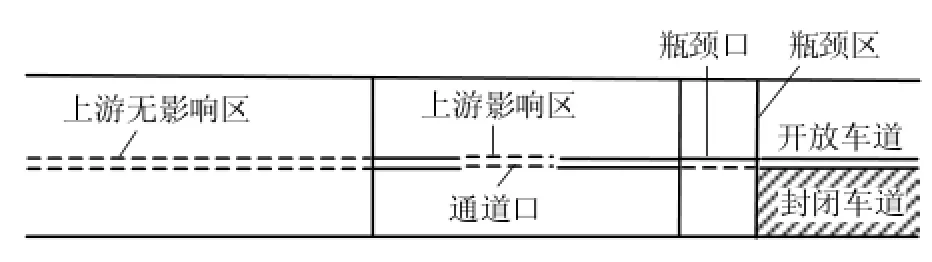
图1 路段结构分布图Fig．1 Themap of typical roadway segment

瓶颈区又分为开放车道与由于临时事件导致的封闭车道；瓶颈口为单向可换道通道，即只有封闭车道车辆可进行换道行为；上游影响区内含双向可换道通道，在该通道两侧车辆可进行换道行为，非通道两侧车辆不可进行换道行为；在上游无影响区，车辆可自由换道．

1．1 直行规则

NS模型虽然形式简单，但可以模拟出绝大多数交通现象，例如，NS模型可以模拟出自发产生的堵塞现象以及拥堵交通情况下的时走时停现象．其更新规则如下：

（1）加速，vn（t＋1）＝min（vn（t）＋1，vmax）；

（2）减速，vn（t＋1）＝min（vn（t＋1），d（t））；

（3）以概率Pslow随机慢化，令

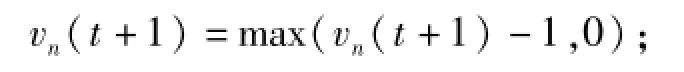
（4）位置更新，xn（t＋1）＝xn（t）＋vn（t＋1），其中，xn表示时刻t车辆n的位置（在车辆行驶方向上递增），单位为cell；vn（t）代表时刻t车辆n的当前车速，单位为cell／仿真步；max（a，b）定义为取a与b中的最大值；min（a，b）定义为取a与b中的最小值；d（t）为时刻t当前车辆与当前车道前方车辆的间距，单位为cell．在比较和计算中，只取d和v的数值．

1．2 换道规则

1．2．1 STCA换道规则

STCA换道车辆在满足安全换道条件下，以换道概率Pst进行换道的行为，其换道条件为

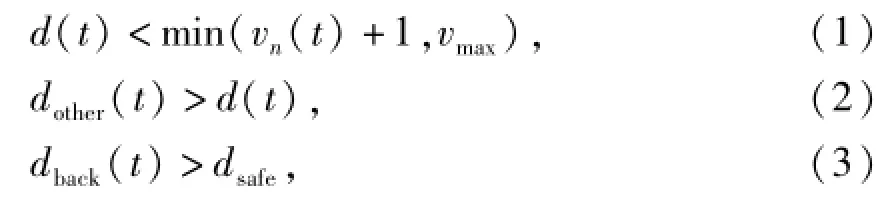
式中：dother（t）和dback（t）为时刻t当前车辆分别与相邻车道前方车辆和相邻车道后方车辆的间距，单位为cell；

dsafe为模型中限定的安全换道间距．

d＜min（vn（t）＋1，vmax）表示当前车辆在其车道受到阻挡；dother（t）＞d（t）表示相邻车道行驶条件优于当前车道；设dsafe＝min（vback（t）＋1，vmax），

其中vback为相邻车道后方车辆的当前车速，则dback（t）＞dsafe，表示换道间距符合安全换道条件，即在相邻车道上，后方车辆无法在单位时间内超越当前车辆．

1．2．2 CABF换道规则

CABF换道规则指车辆在满足换道条件下，以概率Pbf采取强制换道行为的规则，用于描述车流为阻塞流时的换道行为．

（1）换道条件

在非瓶颈口，车辆排队长度较长时，车队后方车辆的驾驶员无法得知车道开放信息，驾驶员根据停车等待时间与车流速度差进行换道行为，此时可采用对称换道规则．在阻塞流中，两条车道车辆的车速差较小，而走-停状态发生十分频繁，故本文采用停车等待时间作为驾驶员换道的主要影响因子．其换道条件为：①与前车距离为0 cell；②与相邻车道前车距离大于0 cell；③停车等待时间tw＞tm，tm为驾驶员能容忍的最大停车等待时间．

在瓶颈口附近，驾驶员能及时了解瓶颈处的交通状态，其换道行为不再是盲目地追随最快车流，而是有目的地换至开放车道，故车辆采取非对称换道规则．其换道条件为：①当前车道为封闭车道；②邻车道前车距离大于0 cell．

（2）换道规则

CABF换道规则主要用于判定两辆争执相同车道的车辆对争执车道的使用权．拥有使用权的车辆可进入目标车道，而未拥有使用权的车辆执行前进规则，但不能通过该冲突位置．CABF换道规则以当前车辆位置和速度的关系作为道路使用权的判定依据．为方便描述，定义变量车辆n的位置当量Фn（t）为车辆位置与当前车速的和，即Фn（t）＝xn（t）＋vn（t）；定义需强制换道车辆为n，被挤车辆为m．

图2为无位置差异车辆的强制换道行为示意图，元胞中数字代表车速，无数字的元胞代表空元胞，以下同．

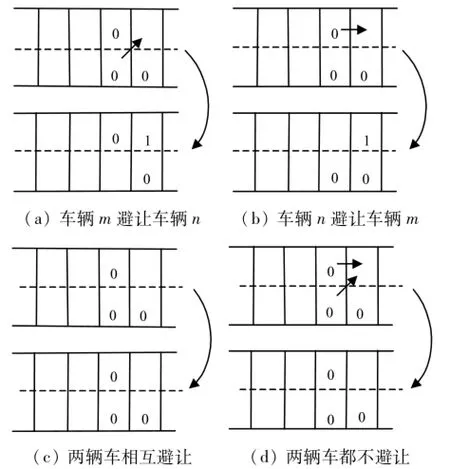
图2 无位置差异车辆的强制换道行为示意图Fig．2 The diagram of forced lane-changing behavior of vehicles without position discrepancy

当头车位置不存在差异时，争执车道使用权取决于其当前速度（或位置当量）的差异，即速度大的车辆具有车道使用权．当其速度相同时，采用同位置且同位置当量的强制换道规则，存在如图2所示的4种情况．其中第4种情况（图2（d））会出现短时间的共同避让现象，其结果是在当前仿真步两辆车都不具有车道使用权．故CABF换道行为的结果为3种：（1）车辆n具有车道使用权；（2）车辆m具有车道使用权；（3）两辆车都不具有车道使用权．该情况描述如下：

当满足Фn（t）≠Фm（t）时：

（1）若Фn（t）＞Фm（t），则Gn＝1，Gm＝0；

（2）若Фn（t）＜Фm（t），则Gn＝0，Gm＝1．

当满足Фn（t）＝Фm（t）时：

（1）以概率p1（1－p2）令Gn＝1，Gm＝0；

（2）以概率（1－p1）p2令Gn＝0，Gm＝1；

（3）以概率（1－p1）（1－p2）＋p1p2令Gn＝0， Gm＝0．

其中Gn（t）＝｛0，1｝表示时刻t车辆n对争执车道的使用权，1表示有使用权，0表示无使用权；p1、p2分别为位置当量相同时车辆n和车辆m的抢道概率．

当车辆位置存在差异时，主要存在以下3种情况，如图3所示．图3（a）中，车辆n与车辆m距离大于1 cell．由于阻塞流中，车辆的平均速度较小，车辆到达换道位置需要较长时间，而车辆n可在该时间内完成换道行为，故此时车辆可直接进行换道．图3（b）和图3（c）中，强制换道车辆n与车辆m

的车辆距离等于1 cell，此时，若忽略车辆m的运行状况而换道会增大事故风险．故此时驾驶员根据感官和经验判断，以车辆位置当量作为换道依据．

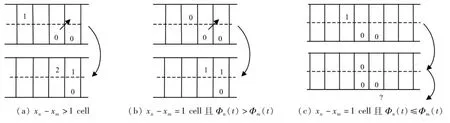
图3 有位置差异的车辆强制换道行为示意图Fig．3 The diagram of forced lane-changing behavior of vehicles with position discrepancy

当车辆n的位置当量大于车辆m的位置当量时，如图3（b）所示，此时车辆m在不加速的情况下，单位时间内无法超越车辆n，即车辆n能在较安全的条件下换道，故此时强制换道车辆n具有车道使用权．图3（c）中，虽然车辆m的位置当量高于或等于车辆n的位置当量，但在堵塞流中，车辆速度较低，并且存在着1 cell的换道空间，此时不同性格的驾驶员会采取不同的驾驶行为．因此，此时应采用同位置且同位置当量的强制换道规则．该情况描述为：

当满足xn－xm＞1或xn－xm＝1 andФn（t）＞Фm（t）时，有Gn＝1，Gm＝0；

当满足xn－xm＝1和Фn（t）≤Фm（t）时，则有：

（1）以概率p1（1－p2）令Gn＝1，Gm＝0；

（2）以概率（1－p1）p2令Gn＝0，Gm＝1；

（3）以概率（1－p1）（1－p2）＋p1p2令Gn＝0，Gm＝0．

1．3 边界条件

边界条件主要分为周期边界条件和开口边界条件．周期边界是指道路始末端相连的边界条件，末端车流状态受初始位置车流状态的影响较大；开口边界条件的特点是边界之间无相互影响．在瓶颈交通流系统中，瓶颈区末端会连接通行能力大于瓶颈区的路段，则瓶颈区交通流不受初始端车流状态的影响，故本文采用开口边界条件．

开口边界包括始端边界和末端边界两部分．车辆在始端边界进入，在末端边界离开．在本文中，发车定义为车辆在始端边界和发车区域（Ucar＝［0，vmax］）中的头车xhead（xhead＜vmax）之间以概率Pcar随机生成，即xnew＝rand（0，xhead）；当发车区域无车辆时，xhead＝vmax－1．生成车辆的初始速度定义为可到达车辆生成位置的随机速度，即v＝rand（xnew，vmax）．末端车辆以超出边界为条件直接消失．

2 仿真分析

文献［19］研究表明，高速公路上占主要成分的车辆平均车身长度为6 m．故本文设仿真元胞长度为7 m（含前后各0．5 m安全距离），设车辆的最大速度vmax＝5 cell／仿真步，道路长度L＝1 200 cell，其中，上游无影响区长度Lno_ctl＝300 cell，上游影响区长度Lctl＝299 cell，瓶颈口长度为1 cell，瓶颈区长度Lneck＝600 cell．设位置当量相同时的抢道概率为p1＝0．5，p2＝0．5，停车等待时间tm＝0 s，仿真步长为1 s．为消除非稳态的影响，连续运行50 000仿真步，分析后1 000仿真步的仿真数据．

2．1 时空图分析

令慢化概率Pslow＝0．1，STCA换道概率Pst＝0．5，当CABF换道概率Pbf分别取0．0和0．5时，利用改进模型对临时瓶颈交通流进行仿真，对比分析两种情况下改进模型对交通流模拟的真实度．图4和图5是交通瓶颈产生于第10 000仿真步、持续时间为500仿真步时，不同CABF概率下仿真的时空斑图．图4给出CABF换道概率为0，即系统只存在STCA换道行为时，系统仿真的时空斑图．从图4可知，STCA换道行为虽然能缓解封闭车道的拥堵排队，但其作用十分有限，两条车道阻塞程度差异较大，这与现实相悖．

在现实交通中，当临时瓶颈形成后，排队车辆驾驶员并不知道车道封闭的信息，为追求最小延误，会强制换道至快车流车道．换道车辆的加入将降低车道车流速度，并形成快车流在两车道之间转换，如此反复换道，产生纳什均衡现象，即车辆在两车道上较均匀地分布．而在只有STCA换道规则的仿真中，所有车辆均会遵守苛刻的换道规则．当密度较高时，车辆难以满足换道要求，封闭车道车辆排队现象严重，因此，形成了两车道上排队车辆分布不均现象．如图5所示，在CABF换道行为加入后，两条车道上车流的堵塞程度相近，封闭车道的堵塞程度甚至略低于开放车道．这说明CABF换道行为能有效地调整两条车道的拥堵程度，也证明了CABF换道规则对于瓶颈交通流模拟的优越性．

图4 CABF换道概率为0．0时系统仿真时空斑图Fig．4 The spatial-temporal pattern of the simulation when the lane-changing probability of CABF is0．0

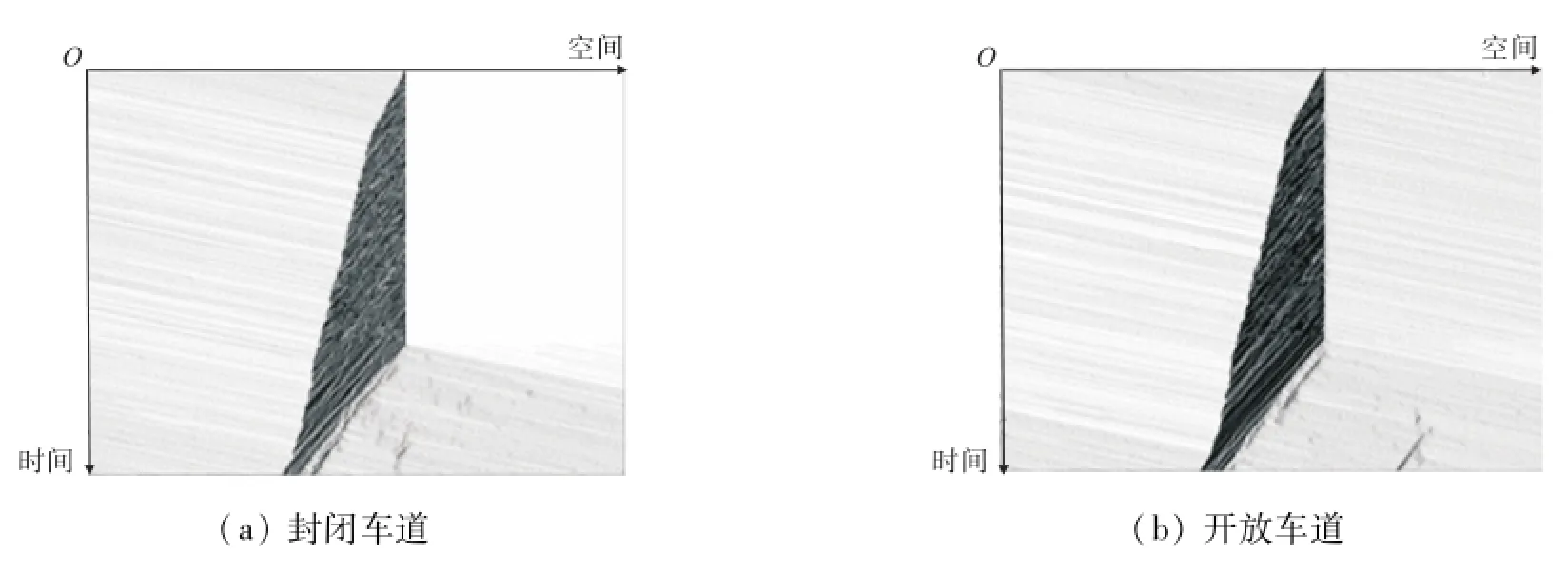
图5 CABF换道概率为0．5时系统仿真时空斑图Fig．5 The spatial-temporal pattern of the simulation when the lane-changing probability of CABF is0．5

2．2 换道概率影响分析

在交通流系统中，换道行为指驾驶员为追求自身最小延误而采取的措施．为研究换道概率对瓶颈交通流的影响，将上游影响区所有元胞设为可换道状态．

STCA换道行为主要用于描述车辆在安全驾驶情况下的换道行为．图6给出了Pbf＝0．5时，不同Pst对瓶颈交通流影响的曲线图．从图6可以看出，STCA换道概率的增加虽然增加了STCA换道频率，但对系统交通流量无显著影响．即STCA换道行为仅影响车辆个体追求最小延误，而不影响瓶颈交通系统的最大流量．

图6 STCA换道概率与瓶颈交通流的关系Fig．6 The relationship between the STCA lane-changing-probability and flow rate at the bottleneck

STCA换道频率是指在单位时间内道路系统中STCA换道行为的次数．图6（a）为STCA换道频率受STCA换道概率影响的曲线图．在STCA换道概率一定的情况下，STCA换道频率随车辆到达率的变化分为两部分：当车辆到达率小于临界车辆到达率（≈0．26）时，系统处于自由流状态，随车辆到达率的增加，STCA换道频率先近似线性地增加，而后减少；当车辆到达率超过临界车辆到达率时，随车辆到达率的增加，STCA换道概率先急速降低，而后缓慢递减．在车辆到达率一定的情况下，当车辆到达率小于临界车辆到达率时，STCA换道频率和最大STCA换道频率与STCA换道概率皆成正相关关系；当车辆到达率高于临界车辆到达率时，STCA换道概率对STCA换道频率的影响小．

瓶颈交通流系统的通行能力与瓶颈区的最大流量密切相关，故本文采用瓶颈区流量作为系统流量进行分析．在图6（b）中，随着STCA换道概率的增加，仅当车辆到达率介于［0．1，0．26］时，瓶颈区的交通流量有微弱的增加，而在其余阶段，瓶颈区流量无显著变化．这是由于在自由流状态车流密度小，车头间距大，故STCA换道需求低．而在堵塞流状态，车流密度大，车头间距小，车辆之间相互作用强，难以满足STCA换道规则苛刻的换道条件．

CABF换道概率指驾驶员为追求最小延误而冒险换道的概率．为研究CABF换道概率对瓶颈交通流的交通影响，利用不同的CABF换道概率Pbf＝｛0．0，0．1，0．2，…，0．8｝对瓶颈交通流进行仿真研究，同时令Pst＝0．5．图7为CABF换道行为对瓶颈交通流影响的曲线图．

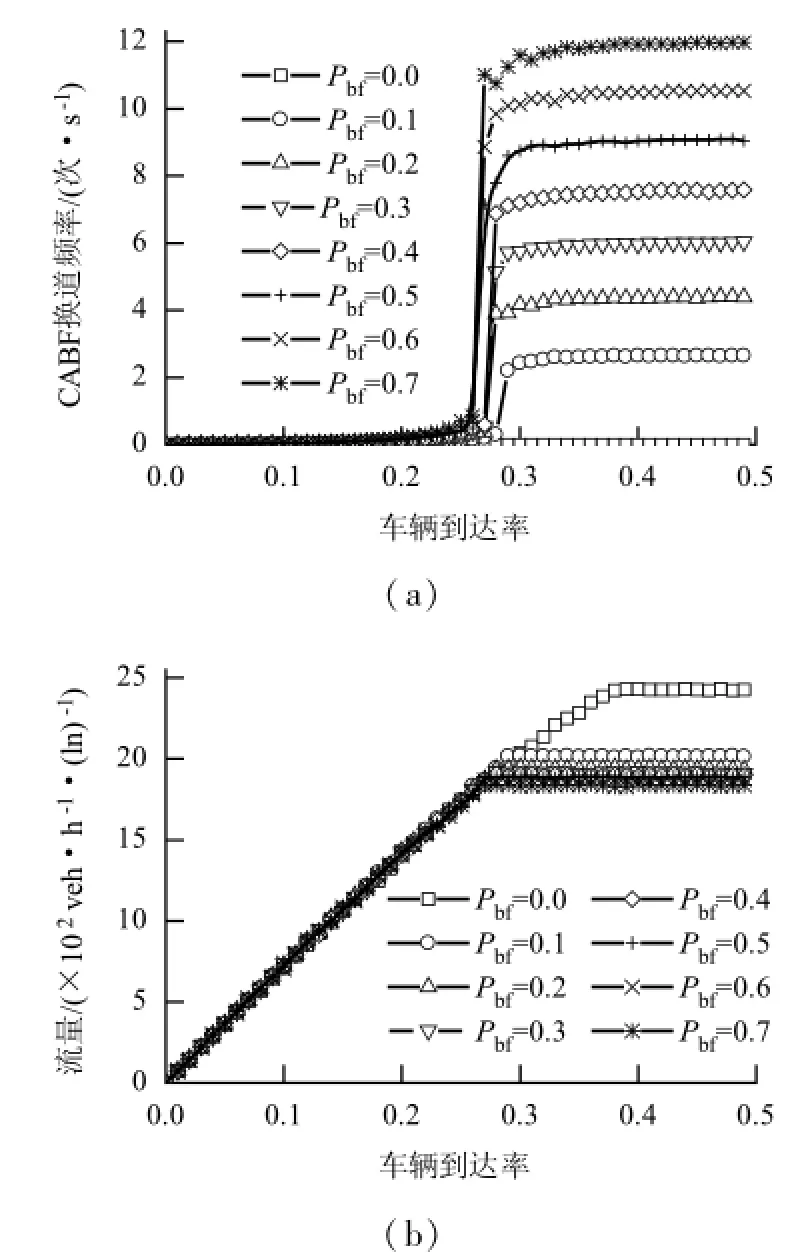
图7 CABF换道概率与瓶颈交通流的关系Fig．7 The relationship between the CABF lane-changing probability and flow rate at the bottleneck

CABF换道频率是指单位时间内车辆进行CABF换道行为的频数．由于CABF换道行为是一种冒险的换道行为，故CABF换道频率在一定程度上反映了系统的交通危险暴露量．根据图7（a）可知，CABF换道行为对系统换道频率的影响分为3个阶段．

第1阶段为低频率阶段．在该阶段，车流处于自由流状态，CABF换道频率低，约为0次／s．当车辆到达率低于0．2时，虽然CABF换道概率增加，但STCA换道行为、CABF换道行为或两者的相互作用使得CABF换道行为需求低；而当车辆到达率达到0．2之后，随车辆到达率的增加，CABF换道频率缓慢增加，曲线开始分离，此时CABF换道行为需求逐渐增大，CABF换道频率开始受CABF换道行为的影响．

第2阶段为第1阶段和第3阶段之间的过渡阶段，也是交通流由自由流到阻塞流的过渡阶段，该区间范围较小．在该阶段随着车辆到达率的增加，CABF换道频率存在剧增现象，且上升速度随CABF换道概率的增加而增加．

第3阶段为高频率阶段，车流在该阶段为阻塞流状态，CABF换道需求大，CABF换道频率随车辆到达率的增加而缓慢增加，直至稳定．并且，当车辆到达率一定时，CABF换道频率随CABF换道概率的增加而成比例增加，这符合随机概率对换道行为的影响规律．

根据图7（b）可知，当CABF换道概率等于0，即不存在CABF换道行为时，系统最大流量远大于存在CABF换道行为的情况；当Pbf由0上升到0．1时，系统最大流量下降了17%，临界车辆到达率下降了24%．这说明CABF换道行为对瓶颈交通流影响的显著性，以及研究瓶颈交通流中CABF换道行为的必要性．

当CABF换道概率大于0后，在自由流状态下，车头间距大，CABF换道需求低，故CABF换道概率对自由流流量无影响，图7（b）中表现为不同CABF换道概率的流量曲线重合．在阻塞流状态，各流量曲线开始出现分支，并达到各自的最大流量，之后趋于稳定，这是由于瓶颈区车流不受外界干扰，其交通量取决于单位时间内进入瓶颈区的车辆数，而当车辆到达率达到临界值后，进入瓶颈区的车辆不再随车辆到达率的增加而变化．

在阻塞流状态，随CABF换道概率的增加，系统的最大流量反而降低．这是因为在瓶颈口附近，由于封闭车道车辆的CABF换道行为打断了开放车道车流的连续性，甚至出现车辆相互避让的现象，造成车辆延误，因此CABF换道行为降低了瓶颈交通流系统的最大流量；而阻塞流状态，车辆较多，车头间距小，排队现象严重，激发了驾驶员的CABF换道行为．这说明CABF换道行为虽然满足了某些个体追求最小延误的目的，但降低了系统运行效率．

结合图7（a）和7（b）可知，在阻塞流状态下，当CABF换道概率从0．1增加到0．8时，临界车辆到达率下降了11%，系统最大流量下降了12%，而CABF换道频率增加了410%．这说明CABF换道行为不仅降低了系统的最大流量，而且大大增加了交通事故的风险．

2．3 冲突点分布影响分析

冲突点为交通流交叉或合流时易引发冲突的地点．在瓶颈交通流系统中，冲突点的分布具有连续性．为研究冲突点分布状况对瓶颈交通流的影响，将冲突点离散为可换道元胞，即可换道元胞处存在可换道通道，车辆可通过该通道换至邻车道．则冲突区间Nen为若干连续可换道通道两侧元胞所构成的区域，冲突点距离Den为上游影响区冲突区间与瓶颈口的距离．

为了解瓶颈口附近的CABF换道行为对瓶颈交通流的影响，本节研究了上游影响区存在一个冲突区间时，不同冲突点距离和冲突区间长度对瓶颈交通流的影响．为排除干扰因素的影响，仿真参数Pst和Pbf取0．5．

冲突点距离表示冲突点的离散程度．当Nen＝1 cell时，不同冲突点距离对瓶颈交通流的影响如图8所示．

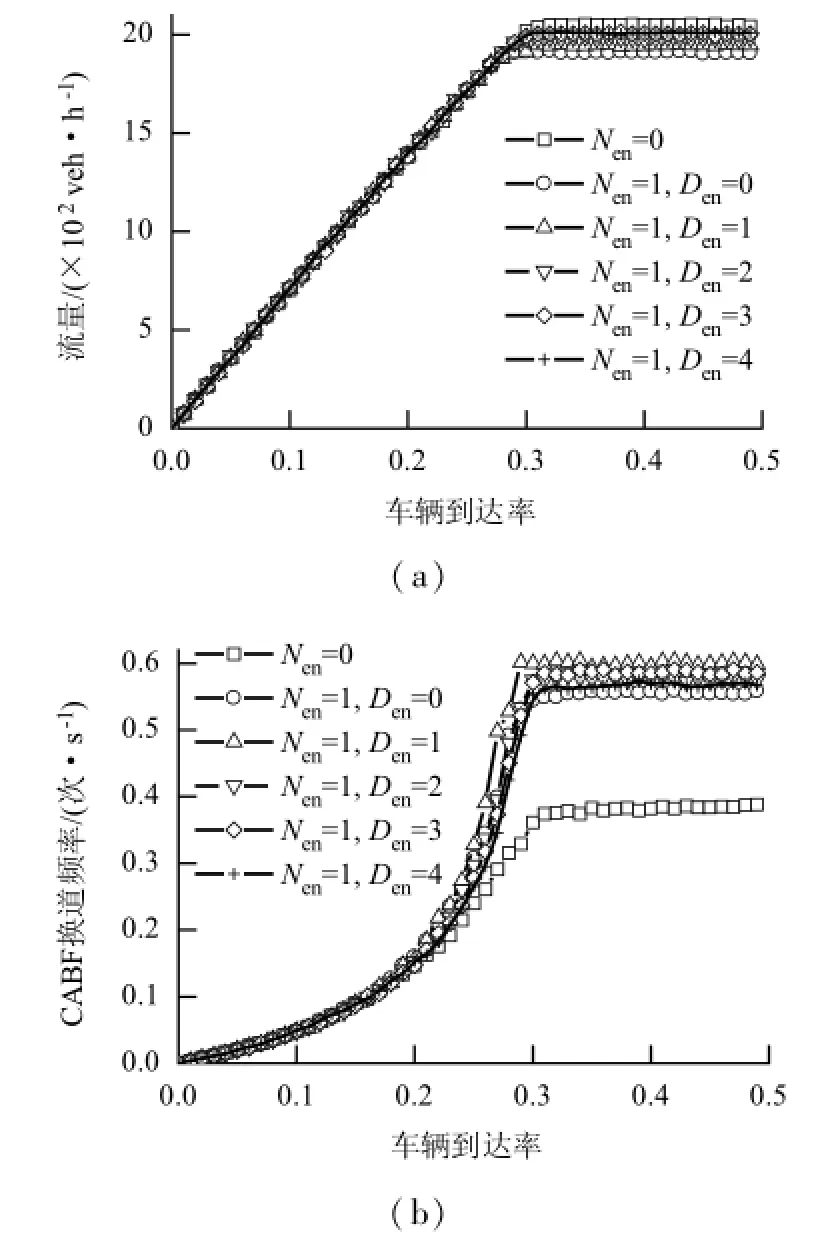
图8 冲突点距离与瓶颈交通流的关系Fig．8 The relationship between the distance between conflict areas and flow rate at the bottleneck

由图8（a）可知，当Nen＝0 cell时，上游影响区不存在可换道通道，第1组数据实际上是冲突点距离为无限大时的仿真结果，此时系统最大流量为2 053 veh／（h·ln），临界车辆到达率为0．32；当Nen＝1 cell，且Den＝0 cell时，第2组数据为上游影响区存在一个与瓶颈口相邻可换道通道时的仿真结果，在该条件下瓶颈口的最大交通流量为1 907 veh／（h·ln），临界车辆到达率为0．28；其它4组数据的流量和临界车辆到达率位于第1组数据和第2组数据之间，且系统流量随Den的增加而增加．

冲突点距离与瓶颈交通流峰值的关系如图9所示．当Nen＝1 cell时，在自由流状态，车流密度小，CABF换道需求低，故冲突点距离的变化对瓶颈区流量无显著影响；在阻塞流状态，瓶颈区达到最大流量，且最大流量随冲突点距离的增加而增加（如图9（a）所示）．这是因为当CABF换道需求一定时，随着冲突点距离的增加，缓解了瓶颈区交通受上游影响区CABF换道的影响．

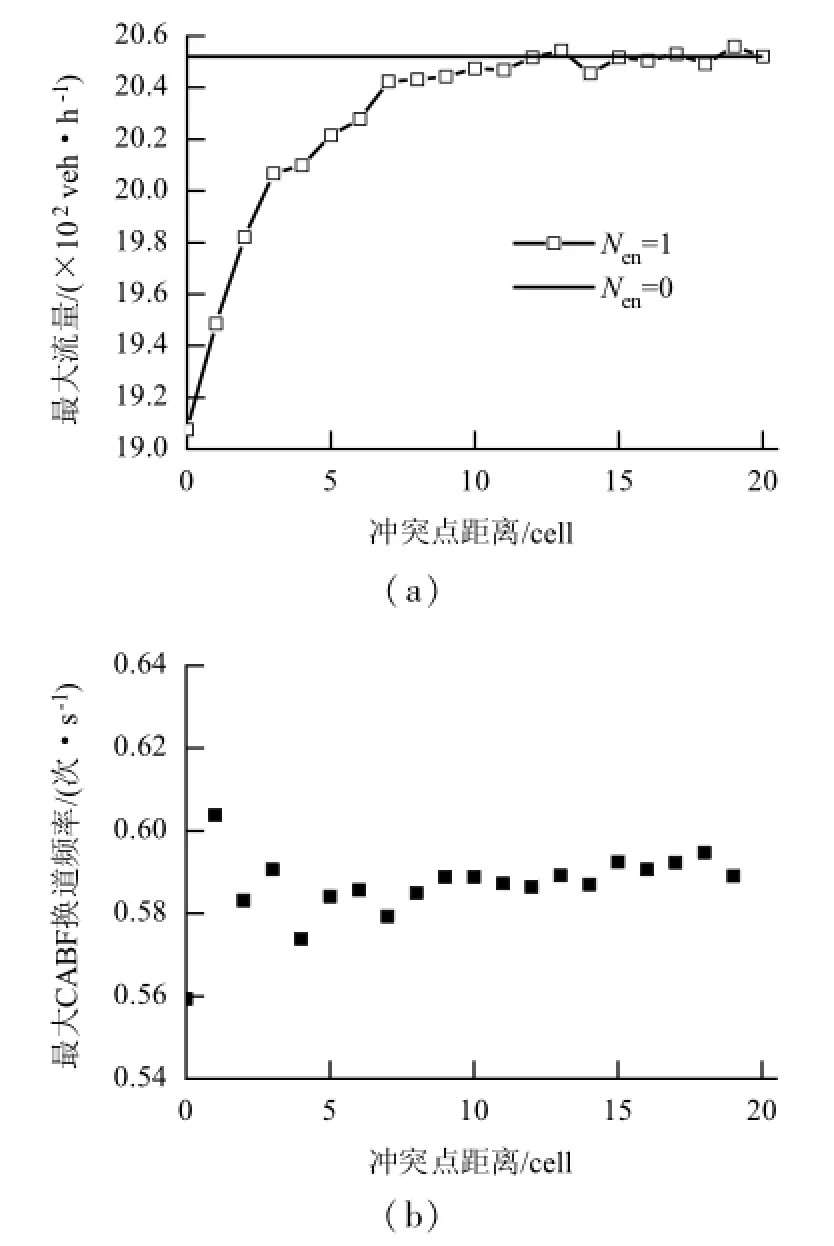
图9 冲突点距离与瓶颈交通流峰值的关系Fig．9 The relationship between peak values and distance between conflict areas at the bottleneck

从图9（b）可以看出，当车辆到达率低于0．18时，不同Den下的CABF换道频率曲线重合，这是因为车流密度小，还未形成排队现象，瓶颈口可满足进入瓶颈区车辆的换道需求．当车辆到达率大于0．18后，曲线开始分离，此时，瓶颈口难以满足封闭车道车辆的换道需求，车辆开始在寻求其他换道通道，故换道通道与瓶颈口的距离差导致了系统流量曲线的分离．当车辆到达率大于临界值后，车流达到系统的最大流量，CABF换道频率趋于稳定，其中冲突区间长度为1 cell时的CABF换道频率远高于冲突区间长度为0 cell时．当冲突点距离为1 cell时，最大CABF换道频率为0．553次／s；当冲突点距离为2 cell时，最大CABF换道频率为0．603次／s，其余冲突区间长度为1 cell的CABF换道频率曲线介于这两条曲线之间，但最大CABF换道频率并未随冲突点距离的增加而单调增减，而是在一定范围内波动变化．

为研究冲突区间长度为1cell时，冲突点距离对最大CABF换道概率的影响，仿真得出了最大CABF换道频率与冲突点距离关系的散点图（图9（b）），从图9（b）可见，最大CABF换道频率随冲突点距离的增加收敛于0．59次／s．当冲突点距离为0和1 cell时，其最大CABF换道频率远远偏离收敛值，且当冲突点距离为0 cell时，CABF换道频率远低于冲突距离为1 cell时的换道频率．这是因为瓶颈口换道环境优于其他位置，以及受瓶颈口车辆换道行为的影响，位于瓶颈口上游附近车辆更愿意通过瓶颈口进入瓶颈区．在仿真模型中表现为CABF换道规则不具有并行性，即前车具有优先更新权，故前车的更新直接影响到相邻后车状态的更新．

总之，冲突点距离的增加不仅降低了冲突频率的收敛程度，而且有效地提高了瓶颈交通系统的最大流量和道路形成拥堵的条件．

为研究冲突区间长度对瓶颈交通流的影响，对冲突点距离Den＝0时，不同冲突区间长度情况下的瓶颈交通流系统进行仿真．通过上述研究发现，主要影响瓶颈交通流的区域为［0 cell，12 cell］，其中最显著区域为［0 cell，7 cell］，故设冲突区间长度Nen＝｛0，1，2，…，7｝cell．图10为不同冲突区间长度对瓶颈交通流影响的曲线图．

由图10（a）可知，当Nen＝0 cell时，系统的最大流量为2 051 veh／（h·ln）；当Nen＝1 cell时，系统的最大流量为1 890 veh／（h·ln），下降了8%；之后最大流量不再随冲突区间长度的增加而显著变化，即冲突区间长度大于两辆车的长度之后，冲突区间长度的增加不再对系统流量产生显著影响．根据图10（b）可知，CABF换道频率、临界车辆到达率与冲突区间长度都成负相关关系，而CABF换道频率曲线从车辆到达率为0．2之后才开始分离，且其斜率随冲突区间长度的增加而增大，这也是图7（b）中出现CABF换道频率急剧上升的原因．这说明虽然冲突区间长度的增加刺激了CABF换道行为的发生，但过于频繁的CABF换道行为不但降低了瓶颈系统的最大流量，而且加大交通事故的风险．

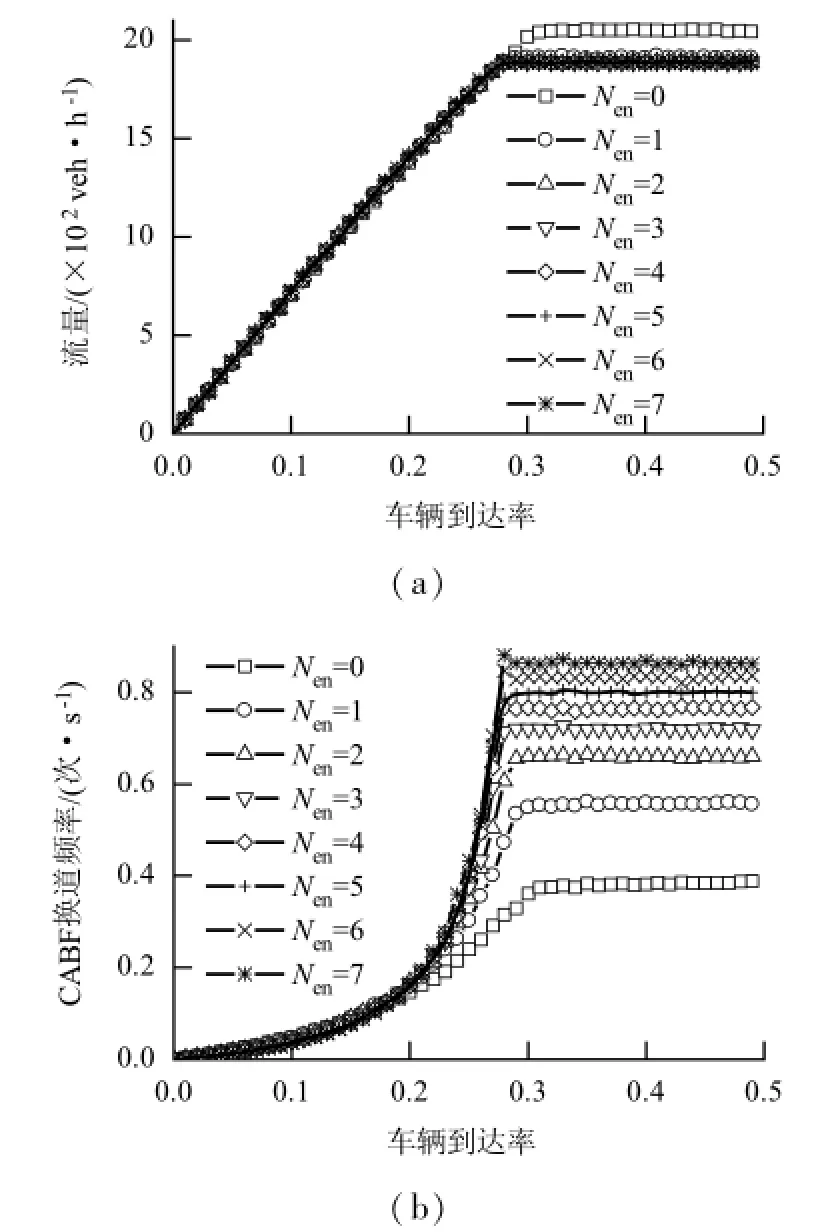
图10 冲突区间长度与瓶颈交通流的关系Fig．10 The relationship between the length of conflict area and flow rate at the bottleneck

3 结 论

在实际的瓶颈交通流中，CABF换道行为对整个交通流产生的影响较大．本文在NS模型的基础上，引入换道规则，提出了适用于单向双车道道路环境下，单车种且无交通指挥员的瓶颈交通流仿真模型．利用开口边界条件，分别在换道概率和冲突点分布不同的情况进行了仿真，分析了安全换道概率、强制换道概率和冲突点分布对临时交通瓶颈系统最大流量和交通事故风险的影响，得出以下结论：

（1）CABF换道规则能有效的模拟瓶颈交通流现象．

（2）STCA换道行为仅对车辆个体追求最小延误有影响，而对瓶颈交通系统最大流量无影响．

（3）CABF换道行为是降低瓶颈交通流量的关键因素，该行为不但降低了系统的最大流量，还增加了交通事故风险．CABF换道行为对瓶颈交通流的影响主要在阻塞流阶段．当车流状态达到临界车辆到达率时，为降低交通事故风险，提高系统最大流量，可采取两车道车流分时段进入瓶颈区和在排队区域临时进行禁止变道管控等措施，以降低CABF换道行为．

（4）系统最大流量受冲突点距离影响较大，冲突点距离在［0 cell，7 cell］时受影响最为显著，在（7 cell，12 cell］时受影响较显著，且与冲突点距离成负相关关系；冲突频率受冲突点距离影响变化较为复杂．为提高瓶颈交通流系统的最大流量，在条件允许时，应在瓶颈口上游［0 cell，12 cell］范围内禁止车辆强制换道；当条件不允许时，应尽量减少瓶颈口附近（［0 cell，7 cell］）车辆的CABF换道行为，且管制力度和管制优先权应与冲突点距离成负相关关系．

（5）系统最大强制换道频率与冲突区间长度成正相关关系，且受其影响显著，而瓶颈交通流系统的最大流量受其影响较小，即冲突区间的增加不仅不利于缓解交通拥堵，而且会加大交通事故风险．故在无条件进行长区间换道行为管制时，应尽量降低冲突区间长度，并且确保车辆能顺利、安全地通过，以降低交通事故风险．

［1］ 孙智勇，孙小端，荣建．高速公路施工区上游过渡区的车辆汇入模型［J］．北方工业大学学报，2013，39（4）：594-598．SUN Zhiyong，SUN Xiaoduan，RONG Jian．Merging model of vehicles on upstream transition area of expressway work zones［J］．Journal of Beijing University of Technology，2013，39（4）：594-598．

［2］ 付蓬勃，吕永波，林琳，等．高速公路意外事件所致堵塞的消散策略研究［J］．北京理工大学学报，2010，30（9）：1051-1055．FU Pengbo，LÜ Yongbo，LIN Lin，et al．Study of the control measures for traffic jam caused by accidents on expressway［J］．Transactions of Beijing Institute of Technology，2010，30（9）：1051-1055．

［3］ 杨庆芳，马明辉，梁士栋，等．高速公路瓶颈区域可变限速阶梯控制方法［J］．西南交通大学学报，2015，50（2）：354-360．YANG Qingfang，MA Minghui，LIANG Shidong，et al．Stair-like control strategies of variable speed limit for bottleneck regions on freeway［J］．Journal of Southwest Jiaotong University，2015，50（2）：354-360．

［4］ 张海军，张珏，杨晓光．异常事件下高速道路交通状态的分析与仿真［J］．交通运输工程学报，2008，8（2）：117-121．ZHANG Haijun，ZHANG Yu，YANG Xiaoguang．Analysis and simulation of traffic state on expressway during incident［J］．Journal of Traffic and Transportation Engineering，2008，8（2）：117-121．

［5］ NAGEL K，SCHRECKENBERG M．A cellular automaton model for freeway traffic［J］．Journal de Physique I，1992，2（12）：2221-2229．

［6］ TAKAYASU M，TAKAYASU H．1／f noise in a traffic model［J］．Fractals，1993，1（4）：860-866．

［7］ LI Xiaobai，WU Qingsong，JIANG Rui．Cellular automaton model considering the velocity effect of a car on the successive car［J］．Physical Review E，2001，64（6）：066128．

［8］ FUKUI M，ISHIBASHI Y．Traffic flow in 1d cellular automata model including cars moving with high speed［J］．Journal of the Physical Society of Japan，1996，65（1）：1868-1870．

［9］ NAGEL K，WOLF D E，WAGNER P，et al．Two-lane traffic rules for cellular automata：a systematic approach［J］．Physical Review E，1998，58（2）：1425-1437．

［10］ CHOWDHURY D，WOLF DE，SCHRECKENBERG M．Particle hopping models for two-lane traffic with two kinds of vehicles：Effects of lane-changing rules［J］．Physica A：Statistical Mechanics and Its Applications，1997，235（3／4）：417-439．

［11］ 郑容森，谭惠丽，孔令江，等．双车道多速车辆混合交通流元胞自动机模型的研究［J］．物理学报，2005，54（8）：3516-3522．ZHENG Rongsen，TAN Huili，KONG Lingjiang，et al．A cellular automaton model for mixing traffic in two-lane system［J］．Acta Physica Sinica，2005，54（8）：3516-3522．

［12］ 王永明，周磊山，吕永波．基于元胞自动机交通流模型的车辆换道规则［J］．中国公路学报，2008，21（1）：89-93．WANG Yongming，ZHOU Leishan，LÜ Yongbo．Lane changing rules based on cellular automaton traffic flow model［J］．China Journal of Highway and Transport，2008，21（1）：89-93．

［13］ 唐夕茹，陈艳艳．基于改进型元胞自动机模型的双车道公路交通特征分析［J］．北京工业大学学报，2014，40（1）：1-10． TANG Xiru，CHEN Yanyan．Traffic characteristic analysis of two-lane highway under the improved ca model［J］．Journal of Beijing University of Technology，2014，40（1）：1-10．

［14］ BIHAM O，MIDDLETON A A，LEVINE D．Selforganization and a dynamical transition in traffic flow models［J］．Physical Review A，1992，46（10）：6124-6127．

［15］ 盛鹏，赵树龙，王俊峰，等．基于元胞自动机模型的道路突发瓶颈现象研究［J］．物理学报，2010，59（6）：3831-3840．SHENG Peng，ZHAO Shulong，WANG Junfeng，et al．Study of temporary traffic bottleneck based on cellular automaton model［J］．Acta Physica Sinica，2010，59（6）：3831-3840．

［16］ 钱勇生，曾俊伟，杜加伟，等．考虑意外事件对交通流影响的元胞自动机交通流模型［J］．物理学报，2011，60（6）：103-112．QIAN Yongsheng，ZENG Junwei，DU Jiawei，et al．Cellular automaton traffic flow model considering influence of accidents［J］．Acta Physica Sinica，2011，60（6）：103-112．

［17］ 赵康嘉，陈淑燕．基于元胞自动机的交通事件交通流仿真模型［J］．公路交通科技，2014，31（3）：133-138．ZHAO Kangjia，CHEN Shuyan．Cellular automaton based traffic flow simulation model for traffic incidents［J］．Journal of Highway and Transportation Research and Development，2014，31（3）：133-138．

［18］ 李庆定，董力耘，戴世强．公交车停靠诱发交通瓶颈的元胞自动机模拟［J］．物理学报，2009，58（11）：7584-7590．LI Qingding，DONG Liyun，DAI Shiqiang．Investigation on traffic bottleneck induce by bus stopping with a two-lane cellular automaton model［J］．Acta Physica Sinica，2009，58（11）：7584-7590．

［19］ 孙德强，刘伟铭．自动发卡条件下公路收费车道的通行能力［J］．公路交通科技，2013，30（8）：129-133．SUN Deqiang，LIU Weiming．Capacity of highway tollgates under automatic card sender condition［J］．Journal of Highway and Transportation Research and Development，2013，30（8）：129-133．

（中文编辑：秦萍玲 英文编辑：兰俊思）

Simulation of Temporary Traffic Bottleneck on Highways Based on Cellular Automaton

JIANG Xinguo1，2， XIA Liang1，2
（1．School of the Transportation and Logistics，Southwest Jiaotong University，Chengdu 610031，China；2．Engineering Laboratory of Integrated and Intelligent Transportation，Chengdu 610031，China）

To study the influence of the forced lane changing and the distribution of conflict points on the temporary traffic bottleneck flow of freeways，a cellular automaton model was proposed considering the driver’s changing psychology behavior．The new model combines the rule of forced lane changing with the NaSch（NS）model and the symmetric two-lane cellular automaton（STCA）model．Under open boundary，the relationship between the traffic flow at the bottleneck，the lane-changing frequency and the car arrival rate were obtained by simulation with different safe lane-changing probabilities，forced lane changing probabilities，distance between conflict areas，and length of conflict area．The results show that safe lane-changing behavior has little influence on the flow．The main factor decreasing the maximum flow is the forced lane changing behavior at the bottleneck．When the safe lane-changing probability is 0．5 and the forced lane changing probability changes from 0．0 to 0．1，the maximum flow decreases by 17%．The length of conflict area helps to reduce the traffic congestion at the bottleneck．When the range length of conflict area changes from 1 to 4 cells，the critical car arrival rate increases by 4%．The traffic conflict area has significant influence on the trafficsafety risk，which could increase with the lane-changing probability．

cellular automaton；traffic bottleneck；forced lane changing；traffic conflict

U412．366

A

0258-2724（2016）01-0128-10

10．3969／j．issn．0258-2724．2016．01．019

2015-03-09

国家自然科学基金资助项目（71271176）；四川省青年基金资助项目（2014JQ0014）

江欣国（1975—），男，教授，博士，研究方向为交通安全，E-mail：xjiang＠swjtu．edu．cn

江欣国，夏亮．基于元胞自动机的高速公路临时瓶颈交通流仿真［J］．西南交通大学学报，2016，51（1）：128-137．