高墩大跨简支梁桥的特殊梁轨纵向力及其影响

张 迅， 苏 斌， 李小珍， 张健强

（西南交通大学土木工程学院，四川成都610031）

高墩大跨简支梁桥的特殊梁轨纵向力及其影响

张 迅， 苏 斌， 李小珍， 张健强

（西南交通大学土木工程学院，四川成都610031）

为探讨主梁收缩与徐变和桥墩梯度温度荷载在高墩大跨简支梁桥中产生的特殊梁轨纵向力，以10跨64 m简支梁桥为工程背景，基于有限元法和梁轨相互作用原理，建立了轨道-梁-墩-基础一体化计算模型，研究收缩与徐变效应、梯度温度模式、墩高等对纵向力的影响规律，并与常规纵向力进行了对比分析．研究结果表明：主梁收缩与徐变引起的梁轨纵向力由纵向缩短效应控制，与竖向挠曲效应关系较小，且该项纵向力大于伸缩力或挠曲力，使得桥台产生较大的水平力；指数分布和线性分布梯度温度模式计算得到的纵向力分别约为制动工况下的20%～30%和50%～100%，指数分布梯度温度模式相对合理，温度曲线参数对纵向力的影响有限，建议尽快制定合理、统一的桥墩梯度温度荷载．

桥上无缝线路；简支梁桥；梁轨相互作用；收缩与徐变；梯度温度

Key words：continuous welded rail on bridge；simply supported beam bridge；bridge-rail interaction；shrink and creep；gradient temperature

梁轨纵向相互作用是无缝线路设计中需要考虑的重要问题之一，其包含伸缩力、挠曲力、制动力和断轨力4项［1-4］，本文称之为“常规梁轨纵向力”．在山区铁路桥梁的建设中，“高墩”、“大跨”和“简支”成为了桥梁结构的几大特色．此时，主梁收缩与徐变以及桥墩梯度温度引起的纵向力问题愈显突出，本文称之为“特殊梁轨纵向力”．

国内外学者对各类桥型的4项常规梁轨纵向力开展了大量的研究，取得了丰硕的成果［5-8］，然而，对于特殊梁轨纵向力的研究极为有限．戴公连等［9］研究了日照温差下无砟轨道主梁变形引起的梁轨纵向力，并讨论了无砟轨道底座板厚度、大气透明度系数和混凝土表面辐射吸收率的影响．刘舟［10］以（40＋56＋40）m高铁连续梁桥为对象，讨论了3种徐变模式下，主梁徐变引起的梁轨纵向力，计算结果显示其在无缝线路纵向附加力的检算中不能忽略．李秋义等［11］以32 m简支梁为对象，研究了桥墩温差荷载引起的钢轨附加力，讨论了墩高、桥墩纵向刚度和桥梁跨数的影响规律，在分析过程中，桥墩温差荷载参照德国铁路桥梁设计规范DS804（B6版）［12］取值．类似地，张迅［13］讨论了该温差荷载作用下，中小跨度连续梁的纵向附加力效应．

上述研究表明，主梁收缩与徐变和桥墩温度荷载均对桥上无缝线路附加力产生影响，但均未涉及具体工程，相关计算参数均过于简化．对于高墩大跨桥梁，不仅主梁收缩与徐变变形大，而且日照作用下的桥墩梯度温度荷载明显［14-16］．基于现有研究成果，本文利用有限元软件建立了高墩大跨简支梁桥的无缝线路纵向附加力计算模型，对规范规定的4项常规梁轨纵向力进行分析，在此基础上，研究了主梁收缩与徐变以及桥墩梯度温度引起的纵向附加力效应，并对相关参数进行分析，给出了荷载组合中二类特殊梁轨纵向力的组合原则．

1 特殊梁轨纵向相互作用

1．1 主梁收缩与徐变效应

轨道铺设完成后，混凝土主梁继续发生收缩与徐变变形，二者同时发生并在桥梁服役期内持续存在．主梁收缩与徐变包括纵向缩短和竖向挠曲二类效应，如图1所示．简支梁在竖向上的变形一般为“上拱”，此时，下翼缘缩短、上翼缘伸长，主梁各截面产生转动，引起上翼缘、下翼缘纵向位移．因此，当收缩与徐变引起主梁上翼缘产生纵向位移时（Δ1和Δ2），由于受到轨道约束，必将在纵向产生梁轨相互作用，此为第一类特殊梁轨纵向力．

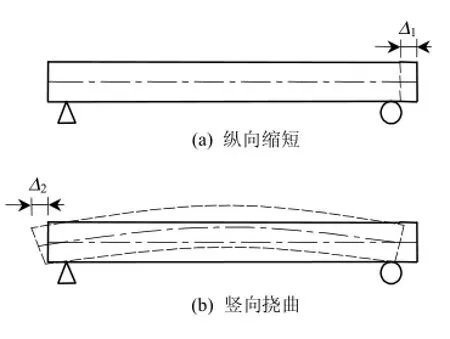
图1 主梁收缩与徐变产生的纵向位移Fig．1 Longitudinal displacement caused by shrink and creep of the main girder

1．2 桥墩梯度温度效应

在日照作用下，桥墩沿线路方向存在梯度温度，使得沿顺桥向两侧边缘纤维伸长不同，产生顺桥向位移并在墩顶达到最大值，如图2所示．墩顶顺桥向位移带动主梁产生纵向变形（Δ3），由于受到轨道约束，必将在纵向产生梁轨相互作用，此为第二类特殊梁轨纵向力．桥墩温差荷载引起的梁轨纵向相互作用，类似于墩底沿纵向的不均匀沉降对桥上无缝线路的影响．

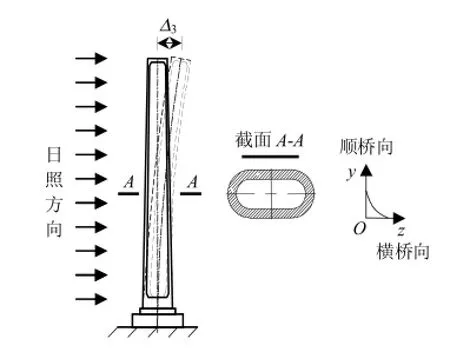
图2 桥墩梯度温度产生的纵向位移Fig．2 Longitudinal displacement caused by the gradient temperature load of a pier

对于桥墩梯度温度取值，我国相关规范并未给出明确规定，文献［4］明确给出了混凝土箱梁在竖向和横向上的梯度温度荷载．目前工程人员大多将规范中适用于混凝土箱梁的温差曲线近似地用于混凝土空心墩中．尽管它们的几何形状较为相似，但空心高桥墩的壁厚要显著大于箱梁的壁厚；同时，桥墩为竖向构件，箱梁为水平构件，二者的方位角有所差异，因此，这种近似处理的准确性有待商榷．文献［14］中对山区铁路高桥墩的现场试验结果表明，不同壁厚桥墩模型的温差曲线均为指数形式，但曲线形状并不完全一致，即壁厚影响了曲线参数，这与规范中采用同一条曲线定义不同壁板厚度箱梁的温差荷载不一致．文献［14］的数值分析结果也证实，对于沿东西走向的桥梁，桥墩西侧壁外表面温度可达到所有方位角中的最大值，此时的温差曲线也是最不利的．

此外，部分文献中采用线性温差曲线描述桥墩梯度温度．例如，德国铁路桥梁设计规范DS804（B6版）［12］，取梯度温度幅值为±5℃，认为桥墩一侧边缘纤维温度比另一侧高5℃，相关研究见文献［11，13］．也有部分研究者考虑一定的安全储备，在具体分析中将该值定为16℃［15］．尽管如此，线性温度梯度模式的合理性有待考量．

2 实例分析

2．1 桥梁概况

某山区铁路桥梁为10跨64 m双线有砟轨道桥梁，如图3所示，设计活载为ZH标准活载．主梁全长为65．1 m，计算跨径为62．9 m，采用等高度单箱单室截面，变截面段长约为8 m．主梁梁高为5．5 m，截面面积为12．78 m2，惯性矩为54．47 m4，中性轴至上翼缘为2．136 m，采用C50混凝土．

桥墩为空心圆端形截面，墩顶尺寸为5．4 m× 10．4 m，纵向和横向坡率外壁为30 cm、内壁为80 cm，墩高为70～74 m，采用C40混凝土．

承台底基础纵向刚度为1 000～1 200 kN／cm．桥上采用Ⅲ型混凝土轨枕，铺设60 kg／m钢轨，处于无缝线路固定区，无伸缩调节器．

图3 桥梁总体布置（单位：m）Fig．3 Layout of the bridge（unit：m）

2．2 计算模型

桥上无缝线路纵向受力分析多采用考虑轨道、主梁、桥墩和基础的一体化计算模型［1，13，16］，如图4所示．该模型采用连接弹簧模拟道床纵向阻力，选用线性或非线性弹簧刚度系数；主梁和桥墩按实际截面建模；墩底使用组合弹簧模拟基础刚度，弹簧刚度系数为常数；采用刚臂连接主梁上翼缘、主梁中性轴和支座，通过释放约束模拟活动支座，以此来协调轨道和主梁之间的纵向变形．

道床纵向阻力r（（kN·m－1）／轨）与钢轨相对扣件的纵向位移x（mm）按文献［2］取值：

有荷载时，机车下r＝11．6x（x≤2．0 mm），r＝23．2（x＞2．0 mm），车辆下r＝7．5x（x≤2．0 mm），r＝15．0（x＞2．0 mm）；

无荷载时，r＝7．5x（x≤2．0 mm），r＝15．0（x＞2．0 mm）．桥梁两端路基固定区长度取为280 m．

本文采用有限元软件ANSYS建立分析模型，其中：钢轨、主梁和桥墩采用Beam188梁单元模拟，单元长度为0．5 m；弹簧单元采用Combin14弹簧单元模拟，道床弹簧采用非线性弹簧刚度系数，基础弹簧采用线性弹簧刚度系数．

图4 桥上无缝线路纵向力计算模型Fig．4 Calculation model of longitudinal force for continuous welded rail on bridge

2．3 常规梁轨纵向力

常规梁轨纵向力包括伸缩力、挠度力、制动力和断轨力4项．

伸缩力计算时，考虑主梁升温15℃；挠曲力计算时，考虑列车前进方向，按双线加载；

制动力计算时，轨面制动力率取0．164，加载长度不超过400 m，按单线加载；

断轨力计算时，按设计锁定轨温上限锁定，并考虑最低轨温时单股钢轨在梁上最不利位置折断，最低降温温差为41．9℃．

加载方法及荷载值按文献［2］中的规定进行．

表1汇总了典型工况下的常规梁轨纵向力计算结果．由表1可知，断轨引起的钢轨拉力最大，其次为制动引起的钢轨拉力和压力；制动工况下的梁轨快速相对位移最大值为3．9 mm，接近文献［2］给定的限值4 mm．由于该桥设计活载大，制动力效应明显，墩台受到的水平力占主导地位；墩台位移在制动工况下的最大值为15．5mm，小于文献［3］给定的限值，L为桥梁跨度）．

表1 常规梁轨纵向力计算结果Tab．1 Calculation results of four common types of longitudinal forces

3 特殊梁轨纵向力

3．1 主梁收缩与徐变引起的纵向力

用ANSYS软件进行混凝土桥梁结构的收缩与徐变计算非常繁琐，为此，本文预先在桥梁专业软件Midas／Civil中进行相关计算．

如前所述，主梁收缩与徐变包含纵向缩短和竖向挠曲二类效应，这二类效应均可方便地通过Midas／Civil软件得到，再以梁单元等效温度荷载的形式施加到ANSYS模型的主梁单元中，相关计算原理见文献［13］．

为便于比较，图5给出了二类效应分别引起的主梁上翼缘纵向位移及其组合，本文将这一工况简称为徐变1．

由图5可以看出：竖向挠曲效应引起的主梁上翼缘纵向位移数值较小，大约从－2．7 mm（固定端）变化至－0．6 mm（活动端）；主梁上翼缘纵向位移主要由纵向缩短效应引起，最大值位于活动端，组合值为－9．8 mm．

对于竖向残余徐变限值，我国规范规定其挠曲变形不得超过20 mm［3］，本文计算得到该主梁的竖向残余徐变为11．9 mm．为了对比，通过调整预应力筋设计，使得竖向残余徐变量达到规范限值（20 mm），再次计算主梁上翼缘纵向位移，并将这一工况简称为徐变2．可以认为工况徐变2是竖向残余徐变极限值，即满足规范要求的最不利情形．

图5 主梁上翼缘纵向位移的组成Fig．5 Longitudinal displacement at the main girder's top flange

计算结果显示：徐变2工况下，主梁上翼缘纵向位移组合值从－4．5 mm（固定端）变化至－12．2 mm（活动端），变化规律与徐变1类似，此处不再赘述．

以上2个工况的对比分析结果表明：主梁上翼缘纵向位移由纵向缩短效应控制，与竖向挠曲效应几乎无关；竖向挠曲变形达到规范给定的限值（20 mm），主梁上翼缘纵向位移也仅增加了约2 mm．因此，为了控制主梁收缩与徐变引起的纵向力，应设法减小主梁纵向缩短量．

图6给出了工况徐变1下的钢轨力和梁轨相对位移．

由图6可以看出：钢轨力在每孔梁的活动端达到最大值，且全桥范围的最大钢轨力出现在右桥台位置，数值为256 kN；梁轨相对位移的变化规律与钢轨力非常相似，并在相邻梁跨交界处出现突变，最大梁轨相对位移约为4．5 mm．

图6 主梁收缩与徐变引起的钢轨力和梁轨相对位移Fig．6 Rail force and relative displacement between bridge and rail caused by shrink and creep of the main girder

需要指出的是：一方面，主梁收缩与徐变需要在数年甚至更长时间才能完成；另一方面，道床纵向阻力的大小受线路养护维修状况影响，且由于列车的动力作用和轨道的翻新等因素，主梁收缩与徐变引起的纵向力在运营期将出现变化或消失．

3．2 桥墩梯度温度引起的纵向力

由于该桥采用有砟轨道，故不考虑主梁的日照温差效应．在分析桥墩梯度温度引起的纵向力时，不考虑桥墩横向温差荷载，因为其不会影响梁轨纵向相互作用．相关文献的研究结果表明［14-15］：日照作用下，墩身高度方向上的温度分布基本均匀、稳定，可以忽略沿墩高方向的微小温度差异．因此，本文假定桥墩纵向温差荷载沿墩高保持不变．

为了便于对比，本文采用3种梯度温度函数进行分析，即Ty1＝23e－9．6y、Ty2＝10e－8y和Ty3＝5（1－y／h）（h为截面高度，y为任意点到截面外边缘的距离，相关参数见图2），并分别简称工况为梯度温度1、梯度温度2和梯度温度3．工况梯度温度1、梯度温度2分别为某高墩公路桥［14］和高墩铁路桥［15］的实测值，为指数分布温差荷载；工况梯度温度3为德国桥梁设计规范DS804（B6版）［12］的规定值，为线性分布温差荷载．

图7～9给出了3种梯度温度工况下，钢轨力、梁轨相对位移和墩台水平力的计算结果．

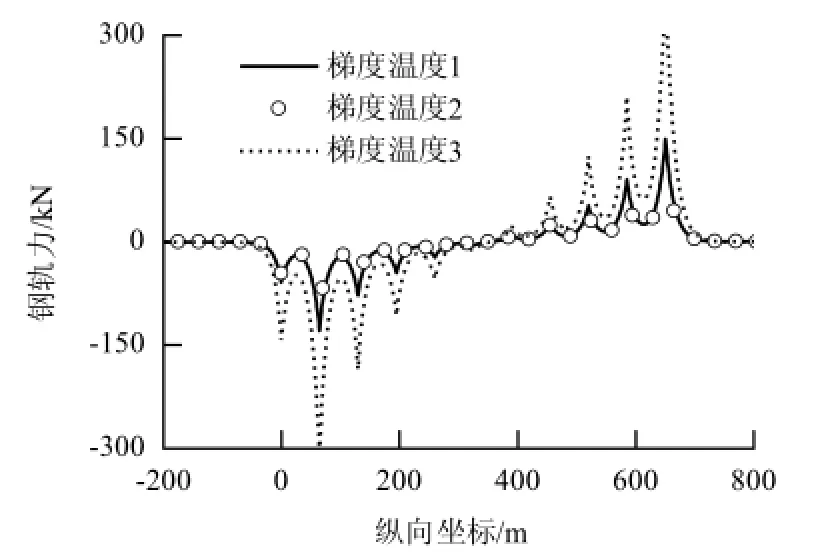
图7 不同梯度温度时的钢轨力Fig．7 Rail forces under different gradient temperatures

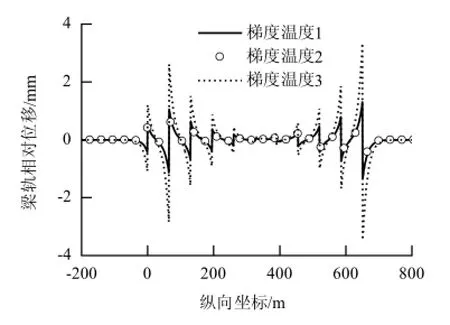
图8 不同梯度温度时的梁轨相对位移Fig．8 Relative displacements between bridge and rail under different gradient temperatures

由图7～9可知：工况梯度温度3下的钢轨力、梁轨相对位移和墩台水平力明显大于工况梯度温度1和梯度温度2，表明线性分布温差荷载产生的梁轨纵向力最为明显．其原因是线性分布温差荷载沿截面高度衰减很慢，特别是对于高墩，由于截面高度很大（本桥为5．4～7．8 m），产生的墩顶纵向位移也很大，由此，导致了梁轨纵向力显著增大；指数分布温差荷载沿截面高度衰减很快，工况梯度温度1和梯度温度2在距桥墩壁面0．5 m左右位置的温度即可下降为0，由此产生的墩顶纵向位移以及梁轨纵向力也要小很多．

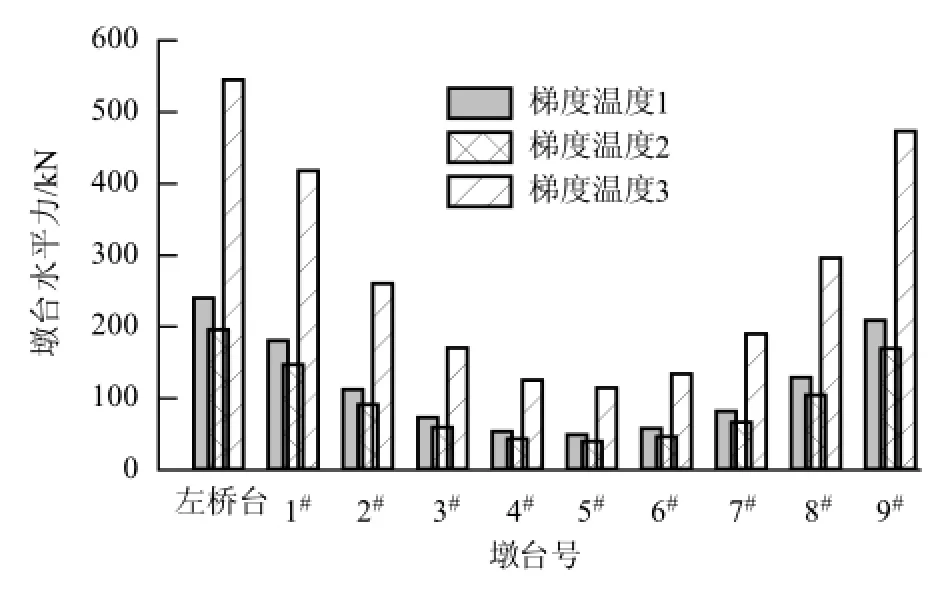
图9 不同梯度温度时的墩台水平力Fig．9 Horizontal forces at tops of pier and abutment under different gradient temperatures

保持其它参数不变，本文计算得到了不同墩高时的最大钢轨力和桥墩水平力，如图10～11所示．

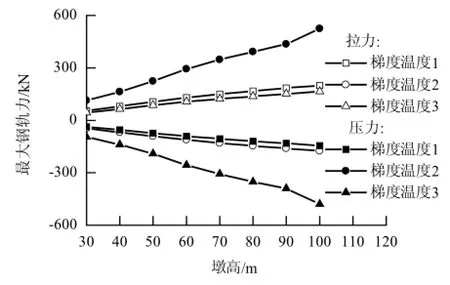
图10 不同墩高时的最大钢轨力Fig．10 The maximum rail forces for different pier heights

图11 不同墩高时的最大桥墩水平力Fig．11 The maximum horizontal forces at pier top for different pier heights

图10～11表明：在墩高较矮时，如30 m墩高时，工况梯度温度3得到的最大钢轨力和桥墩水平力稍大于另外2个计算工况；随着桥墩高度增加，桥墩截面高度也不断增大，最大钢轨力和桥墩水平力也不断增加，且增加速率越来越快，导致工况梯度温度3的计算结果逐渐偏离另2个计算工况；工况梯度温度1和梯度温度2得到的最大钢轨力和桥墩水平力相差不大，说明梯度温度曲线的具体参数对梁轨纵向力的影响有限．

综合以上分析结果，线性分布梯度温度模式在墩高较高时将产生非常极端的计算结果，所以该梯度温度模式的合理性有待进一步研究．

4 不同纵向力效应的对比

文献［2］规定：同一股钢轨的伸缩力、挠曲力、断轨力相互独立，不作叠加；伸缩力、挠曲力、断轨力不与同线制动力组合；伸缩力或挠曲力按主力考虑，制动力按附加力考虑，断轨力按特殊荷载考虑；荷载组合按照文献［3］确定．然而，相关规范并未明确二类特殊梁轨纵向力应如何进行组合．根据二类特殊梁轨纵向力的产生机理，本文认为主梁收缩与徐变引起的纵向力应按主力考虑，高墩梯度温度引起的纵向力应按附加力考虑，与文献［2］中的各项荷载的分类原则一致．因此，对于高墩大跨桥梁，无缝线路纵向附加力的荷载组合总体上应按以下原则进行：

（1）主力组合：伸缩力或挠曲力的较大者＋主梁收缩与徐变引起的纵向力；

（2）主力与附加力组合：主力组合＋制动力＋高墩梯度温度引起的纵向力；

（3）主力与特殊荷载组合：主力组合＋断轨力．

为了明确二类特殊梁轨相互作用力的影响，图12～14汇总了不同纵向力效应下的最大钢轨力、梁轨相对位移和墩台水平力．

由图12～14可知：主梁收缩与徐变引起的纵向力效应（徐变1和徐变2）不容忽视，其引起的钢轨力、梁轨相对位移和墩台水平力均要大于伸缩力或挠曲力效应，特别是桥台水平力要大得多；桥墩梯度温度引起的纵向力效应（梯度温度1、梯度温度2和梯度温度3）小于制动力效应；指数分布梯度温度模式计算得到的钢轨力、梁轨相对位移和墩台水平力约为制动工况下的20%～30%，而对于线性分布梯度温度模式，这一比例约为50%～100%．

图12 不同纵向力效应下的最大钢轨力Fig．12 The maximum rail forces caused by different longitudinal forces

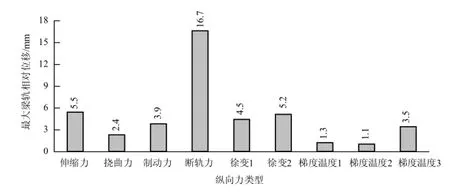
图13 不同纵向力效应下的最大梁轨相对位移Fig．13 The maximum relative displacements between bridge and rail caused by different longitudinal forces

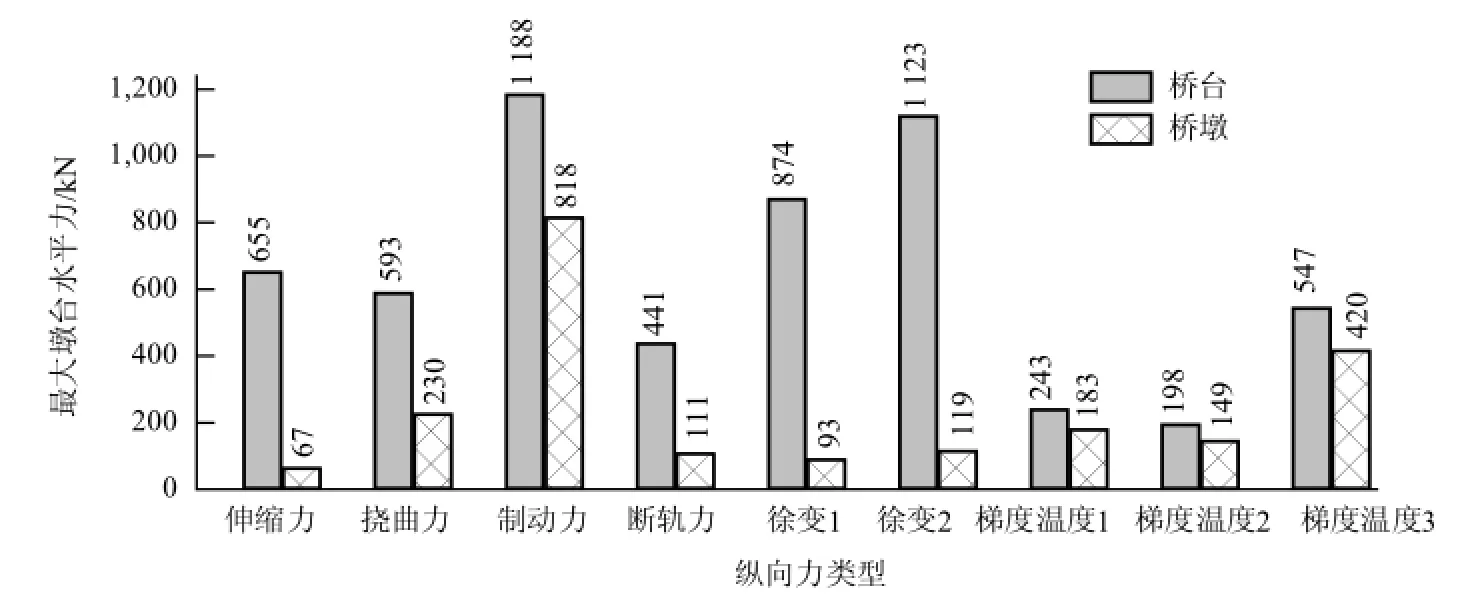
图14 不同纵向力效应下的最大墩台力水平力Fig．14 The maximum horizontal forces at tops of pier and abutment caused by different longitudinal forces

5 结 论

（1）主梁收缩与徐变引起的上翼缘纵向位移主要由纵向缩短效应引起，与竖向挠曲效应几乎无关．为了控制主梁收缩与徐变引起的纵向力，应减小主梁纵向缩短量．

（2）对于桥墩梯度温度荷载，线性分布梯度温度模式衰减慢，如用于截面高度很大的高墩桥梁进行纵向力计算，将得到非常极端的计算结果；指数分布梯度温度模式衰减快，梯度温度曲线的具体参数对梁轨纵向力的影响有限．

（3）主梁收缩与徐变引起的纵向力效应比伸缩力或挠曲力效应明显，特别是对桥台产生更不利的水平力；指数分布和线性分布梯度温度模式计算得到的各项纵向力效应分别约为制动工况下的20%～30%和50%～100%．

桥墩梯度温度模式决定了引起的纵向力大小，并在某种程度上成为了高墩大跨桥梁无缝线路设计中的控制因素．建议尽快制定合理、统一的桥墩梯度温度荷载，以利于该类桥梁的无缝线路设计．

［1］ 广钟岩，高慧安．铁路无缝线路［M］．北京：中国铁道出版社，2012：25-56．

［2］ 中华人民共和国铁道部．TB 10015—2012铁路无缝线路设计规范［S］．北京：中国铁道出版社，2012．

［3］ 中华人民共和国铁道部．TB 10002．1—2005铁路桥涵设计基本规范［S］．北京：中国铁道出版社，2005．

［4］ 中华人民共和国铁道部．TB 10002．3—2005铁路桥涵钢筋混凝土和预应力混凝土结构设计规范［S］．北京：中国铁道出版社，2005．

［5］ RUGE P，BIRK C．Longitudinal forces in continuously welded rails on bridgedecks due to nonlinear trackbridge interaction［J］．Computers＆Structures，2007，85（7）：458-475．

［6］ OKELO R，OLABIMTAN A．Nonlinear rail-structure interaction analysis of an elevated skewed steel guideway［J］．Journal of Bridge Engineering，2010，16（3）：392-399．

［7］ YAN B，DAI G L，ZHANG H P．Beam-track interaction of high-speed railway bridge with ballast track［J］．Journal of Central South University，2012，19（5）：1447-1453．

［8］ CHEN R，WANG P，WEI X K．Track-bridge longitudinal interaction of continuous welded rails on arch bridge［J］．Mathematical Problems in Engineering，2013，Article ID 494137．

［9］ 戴公连，郑鹏飞，闫斌，等．日照作用下箱梁桥上无缝线路纵向力［J］．浙江大学学报：工学版，2013，47（4）：609-614．DAI Gonglian，ZHENG Pengfei，YAN Bin，et al．Longitudinal force of CWR on box girder under solar radiation［J］．Journal of Zhejiang University：Engineering Science，2013，47（4）：609-614．

［10］ 刘舟．收缩徐变和日照温差对高铁连续梁桥梁轨纵向力影响研究［D］．长沙：中南大学，2012．

［11］ 李秋义，孙立．桥墩温差荷载引起的桥上无缝线路钢轨附加力［J］．中国铁道科学，2007，28（4）：50-54．LI Qiuyi，SUN Li．Additional longitudinal force of CWR track on bridge caused by temperature difference between one side and another side of pier［J］．China Railway Science，2007，28（4）：50-54．

［12］ DB NETZ A G．DS804（B6）vetschrift for eisenbahnbrchen and sonstige ingenirurbauwerke［S］．Müfinchen：Dontche Bahn Gruppe，2000．

［13］ 张迅．常用跨度连续梁桥墩顶纵向水平线刚度限值研究［D］．成都：西南交通大学，2008．

［14］ 蒋国富．大跨径桥梁高墩日照温度效应的研究［D］．西安：长安大学，2005．

［15］ 武立群．混凝土箱梁和空心高墩温度场及温度效应研究［D］．重庆：重庆大学，2012．

［16］ 刘婷林，代先星，肖杰灵，等．温度梯度对高墩桥上无缝线路的影响分析［J］．铁道建筑，2014（4）：121-124．

（中文编辑：秦 瑜 英文编辑：兰俊思）

Special Longitudinal Forces between Continuous Welded Rail and Long-Span Simply Supported Beam Bridge with High Piers and Their Influences

ZHANG Xun， SU Bin， LI Xiaozhen， ZHANG Jianqiang
（School of Civil Engineering，Southwest Jiaotong University，Chengdu 610031，China）

In order to investigate the special longitudinal forces between a continuous welded rail and a bridge caused by shrink and creep of the main girder and gradient temperature load of piers，a simply supported beam bridge with a standard span of64 m was selected as the case study，and an rail-girder-pier-foundation integrated calculation model was established by finite element method（FEM）and bridge-rail interaction theory．On this basis，the influence laws of shrink and creep effects，gradient temperature modes，and pier height on longitudinal forces were probed into in comparison with four common types of longitudinal forces．The results show that the longitudinal force induced by shrink and creep of the main girder is dominated by the longitudinal shortening effect rather than the vertical bending effect．This kind of longitudinal force is higher than the contractility or bending force，and it causes a large horizontal force at abutments．The longitudinal forces caused by gradient temperature in exponential and linear distribution modes account for 20%-30%and 50%-100%，respectively，of the case of brake force．In general，the exponential distribution mode of gradient temperature is more reasonable as different parameters result in limited variations in longitudinal forces．Due consideration should be given to the formulation of reasonable and uniform gradient temperature load of piers．

U213．9

A

0258-2724（2016）01-0057-08

10．3969／j．issn．0258-2724．2016．01．009

2015-07-16

国家自然科学基金资助项目（51308469，51378429）；中央高校基本科研业务费专项资金资助项目（2682014BR053）

张迅（1985—），男，讲师，博士，研究方向为桥梁结构动力响应，E-mail：zhxunxun＠swjtu．edu．cn

李小珍（1970—），男，教授，博士，研究方向为桥梁结构动力响应，E-mail：xzhli＠swjtu．edu．cn

张迅，苏斌，李小珍，等．高墩大跨简支梁桥的特殊梁轨纵向力及其影响［J］．西南交通大学学报，2016，51（1）：57-64．