利用钢轨位移测定垂向轮轨力的探究

刘可达

(同济大学铁道与城市轨道交通研究院，上海 201804)

利用钢轨位移测定垂向轮轨力的探究

刘可达

(同济大学铁道与城市轨道交通研究院，上海 201804)

分别利用连续弹性支撑梁模型和弹性点支撑梁模型，测定了钢轨位移，确定了垂向轮轨力，并通过试验，获取了扣件垂向刚度，在试验线路测试了车辆以不同速度通过测点时的轮轨力和位移数据，通过对比实测值与计算值，证明利用所测钢轨位移在连续弹性梁模型和弹性点支撑模型下求得的垂向轮轨力满足精度要求。

测力钢轨法，轨道模型，钢轨位移，垂向轮轨力

轮轨间的相互作用力(简称轮轨力)主要包括车轮和钢轨之间的垂向力、横向力和纵向力［1，2］。轮轨力若超出限制范围，将加剧结构振动和车轮、钢轨的磨耗，降低其使用寿命，严重时将导致车辆脱轨。因此，轮轨力检测对列车运行时的安全性和舒适性十分重要。

目前，轮轨力测试方法主要有2种，分别是测力轮对法和测力钢轨法［3，4］。测力轮对法采用在轮对上贴应变片，通过车轮的变形来获取轮轨力;测力钢轨法是在轨道上选择测试区域，在指定断面上粘贴应变片，通过钢轨变形获取轮轨力［5］。与测力钢轨法相比，测力钢对法虽然可以通过测量车轮辐板有限点的应变实现轮轨力的连续监测，但是该方法在测试前需用测试轮对替换普通轮对，若要监测线路上所有车辆的运行状态，需要在每辆车上更换测力轮对，显然这种方法是不现实的。测力钢轨法弥补了测力轮对法的上述缺陷，李奕璠等人在此基础上提出了测力钢轨的连续输出算法来弥补测力钢轨法不能进行连续输出的缺陷，可见测力钢轨法在钢轨力的测量上已具备经济性和实用性［6，7］。但是，在钢轨上粘贴应变片仍然是一项复杂的前期工作，不仅需要对钢轨进行充分打磨，投入大量的人力，操作过程中的人为失误也将使得测试结果产生误差，除此以外，通常贴片不可重复使用，测试过程中还易受到电磁干扰。基于以上的不足，本文提出通过测量钢轨位移获取垂向轮轨力的方法，激光测距技术目前已十分成熟，具有精度高稳定性好等优点［8］。利用成熟的激光测距技术，在已知扣件刚度的条件下测试钢轨位移，基于连续弹性梁模型和弹性点支撑梁模型的计算理论推算轮轨力，本文对此进行探讨，尝试验证该方法的可行性。

1 扣件静刚度测试

通过室内试验利用申克机对文中所使用的单个扣件刚度进行测试。试验前，试件和试验所用所有部件和设备在试验环境中静置24 h。将试件和试验装置安放在试验机上，用扭矩300 N·m ±50 N·m将试件与支撑钢板拧紧在一起。垂向静刚度测试安放顺序为:支承钢板、被测试件、轨下胶垫、短钢轨，如图1所示;具体的垂向静刚度测试安装如图2所示。按照记录的力和位移的数据，绘制力—位移曲线(见图3)，计算得到扣件垂向静刚度。

2 激光位移计获取钢轨位移

为获取在列车运行时的钢轨位移，在“同济大学轨道交通综合试验线”上使用激光位移传感器进行钢轨位移测试试验。试验段线路为直线段平坡轨道，扣件的间距按照600 mm布置，并按标准要求进行安装;轨道结构中，道床厚度610 mm;钢轨60 kg/m。试验段轨道长度为30 m长无砟轨道，主要考虑试验段轨道长度不小于单节试验车辆长度。在轮轨力测量位置布置激光位移传感器，测量跨中处竖向位移，测点布置在两根钢轨的外侧。设置了1，2，3，4四个测点，如图4所示。

图1 垂向静刚度测试加载方法示意图

图2垂向静刚度测试实际操作示意图

图3 力—位移曲线

图4测点布置图

在道床板上合适的位置处粘贴铁片，以便于装有激光位移传感器的磁铁底座固定，安装激光位移传感器，将其射线发射处大致对准布置好的测点。使用CD5-W85型传感器测量垂向位移。依次记录试验车辆20 km/h，30 km/h，40 km/h各两个来回的测试数据。

3 理论分析和计算

3.1 连续弹性梁模型下钢轨位移与荷载关系验证

将钢轨与扣件系统简化为连续梁结构，截取其中一段，见图5。

跨中受集中荷载P，端点弯矩为M，温度应力为N，EI为钢轨的抗弯刚度，H为端部抗弯刚度，根据材料力学理论，挠曲性方程

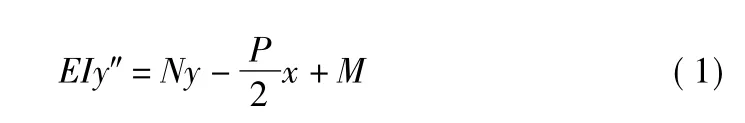
图5 钢轨受力示意图

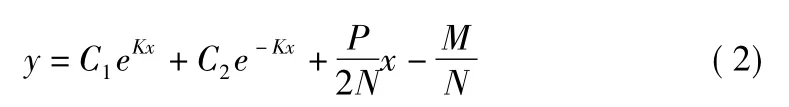
解方程组得:

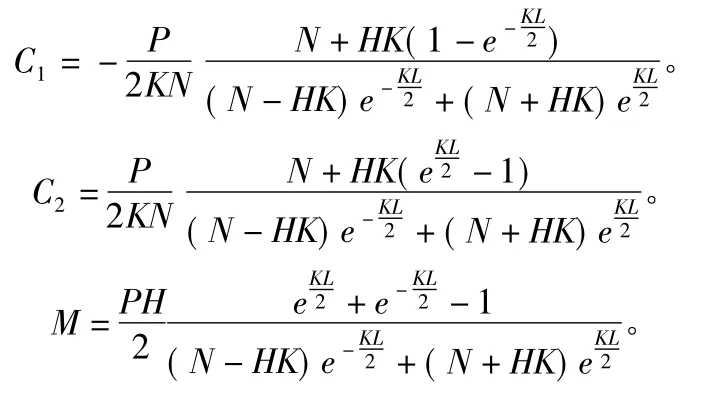
假设

其中影响跨中位移的变量为P，N，H，假定H=50 kN/mm，P和N对挠度δ的影响如图6所示的值反映了集中荷载与挠度的线性关系。

图6 温度力对垂向挠度的影响

由图6可以看出，温度力N对挠度的影响十分小，若不考虑温度力N，则跨中挠度公式如下:

可见，温度力对施加荷载时的跨中挠度影响可以忽略不计，不考虑温度力时，跨中位移与集中荷载为线性关系。

3.2 基于连续弹性支撑梁模型的垂向轮轨力计算

连续弹性支撑梁模型基于钢轨的抗弯刚度作用，将轨枕对钢轨的支撑视为连续支撑［9］，如图7所示，D为钢轨支座刚度，d为两轨枕之间距离为单位钢轨产生单位下沉所需的分布力。

图7 钢轨连续支撑示意图

当钢轨距离测点O距离为L处受一大小为P的垂向荷载，测点O由于垂向力P而产生的位移由下式表示:

3.3 有限元模型计算

基于弹性点支撑模型，把轨下结构描述为一系列相隔轨枕间距的离散弹性—阻尼点支撑体系［10］，利用ABAQUS建立试验轨道静力模型，如图8所示，其中扣件系统用弹簧单元模拟。计算钢轨在试验中所测位移对应的轮轨力。

图8FEA模型计算结果

4 轮轨力计算结果对比分析

利用式(6)可以通过已知的扣件刚度和钢轨位移进行计算。

垂向轮轨力计算见表1。

表1 垂向轮轨力计算

在连续弹性支撑梁模型下的垂向轮轨力计算值与实测值的平均误差为2.2%，弹性点支撑理论下利用有限元模型所得的垂向轮轨力计算值与实测值的平均误差为1.6%，可见理论计算值与实测值误差较小，满足精度要求。

5 结语

钢轨的垂向位移与垂向轮轨力之间理论上是存在一一对应的关系，在已知扣件刚度的前提下，利用成熟的激光测距技术测量钢轨跨中位置的垂向位移，利用连续弹性支撑梁模型可以求得处挠度方程为:垂向轮轨力，与现场贴片试验测得的垂向轮轨力进行对比，误差较小，也可以通过建立有限元模型，利用所测得的位移计算垂向轮轨力，精度同样满足要求。

［1］ 刘建新，易明辉，王开云.重载铁路车轮踏面擦伤时的轮轨动态相互作用特征［J］.交通运输工程学报，2010，10(3): 52-56.

［2］ 陈建政.轮轨作用力和接触点位置在线测量理论研究［D］.成都:西南交通大学，2008.

［3］ Akira，Matsumoto，曲文强.一种测试轮轨力的新方法［J］.国外铁道车辆，2013，50(4):89-90.

［4］ 杨 潇.基于轮轴应力的轮轨力检测方法研究［D］.成都:西南交通大学，2014.

［5］ 杜彦良，张文涛.基于光纤激光传感器的重载铁路列车在途安全状态监测技术［J］.中国工程科学，2009，11(10):61-66.

［6］ 李奕璠，刘建新，王开云，等.测力钢轨轮轨力连续输出的算法研究［J］.交通运输工程学报，2011，11(4):36-40.

［7］ 赵国堂.铁路轨道刚度的确定方法［J］.中国铁道科学，2005，26(1):1-6.

［8］ 金 鑫，金新灿，龚 明，等.基于轮轴动应力测试的轮轨力识别与分析［J］.北京交通大学学报(自然科学版)，2012，36 (4):173-177.

［9］ 陈秀芳.轨道工程［M］.北京:中国建筑工业出版社，2004: 172-179.

［10］ 农汉彪.轮轨垂向载荷连续测量与识别方法研究［D］.成都:西南交通大学，2007.

Exploration the vertical wheel/rail force using rail displacement determination

Liu Keda
(Railway and Urban Rail Transit Institute，Tongji University，Shanghai 201804，China)

Respectively using the continuous elastic support beam model and elastic point support beam model，this paper tested the rail displacement，determined the vertical wheel/rail force，and through the test，obtained the fastener vertical stiffness，in test line tested the wheel/rail force and displacement data of the vehicle taking different speed through measurement point，by comparing the measured values and calculated values，proved the vertical wheel/rail force met the accuracy requirement by using the measured rail displacement in continuous elastic beam model and elastic support model.

dynamometry rail method，rail model，rail displacement，vertical wheel/rail force

U213.2

A

1009-6825(2016)35-0145-03

2016-10-10

刘可达(1991-)，男，在读硕士