不可约非奇异M矩阵的Hadamard积最小特征值的新估计

李艳艳

（文山学院数学学院，云南 文山 663000）

不可约非奇异M矩阵的Hadamard积最小特征值的新估计

李艳艳

（文山学院数学学院，云南 文山 663000）

借助圆盘定理，不可约非奇异M矩阵A的逆矩阵A-1的元素的新估计式，得到了不可约M矩阵B与A-1的Hadamard积的最小特征值τ（B。 A-1）的新估计式，并且从理论上证明了该式子提高了李华在文献①李华,刘玉晓,刘常盛：《矩阵Hadamard积最小特征值的新界值估计》，《重庆师范大学学报（自然科学版）2014年第31期，第54-57页。中给出的相应结果。

非奇异M矩阵；Hadamard积；最小特征值；估计式

1 预备知识

Cn×n（Rn×n）表示n阶复（实）矩阵的集合，Mn表示非主对角元非正，逆矩阵的元非负的矩阵的集合，并称这类矩阵是非奇异M矩阵。τ（A）表示非主对角元非正的A矩阵的最小特征值。A。 B表示矩阵A和B的对应元素相乘所得的矩阵，称为A与B的Hadamard积。

引理1②Fiedler M,Markkam T,"An inequality for the Hadamard product of an M matrix and inverse Mmatrice.lin Alj Appl,1988,101:pp.1-8.设A,B,C,D∈Rn×n，其中C,D是正对角矩阵，则D（A。B）E=（DAE）。B=（DA）。BE=（AE）。（DB）= A。（DBE）

引理2③同①。设A=（ai）j∈Cn×n,则A的所有特征值都位于下列区域

引理3④赵建兴：《M-矩阵最小特征值估计及其相关问题研究》，云南大学博士学位论文，2014年。设A=(aij)∈Cn×n是行严格对角占优的M矩阵，A-1=(βΙJ),则

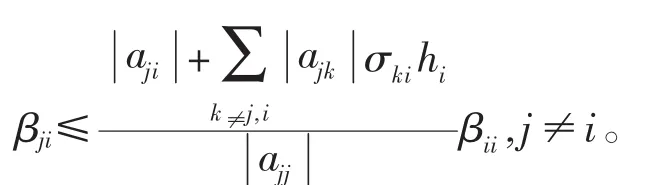
引理4⑤同①。若A,B∈Mn,则B。 A-1∈Mn。

引理5⑥同①。若A∈Mn，那么存在正向量v，使得vTA=τ（A）v,v称为A的右Perron特征向量。

2 主要结论

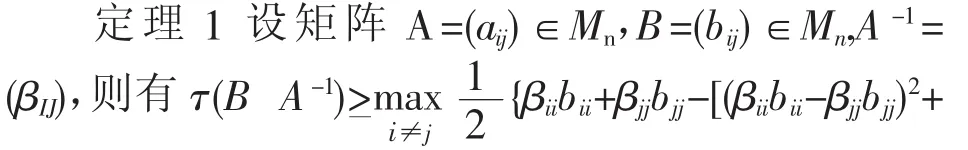
即定理1的估计式提高了文献①李华,刘玉晓,刘常盛：《矩阵Hadamard积最小特征值的新界值估计》，《重庆师范大学学报》（自然科学版）2014年第31期，第54-57页。的相应结果。

则结果得证。

The new estimates of the minimum eigenvalue of the Hadamard product for nonsingular irreducible M matrix

LI Yanyan

Using the disc theorem and the new estimate of the elements of the inverse matrix A-1of a nonsingular M matrix A, A new estimateτ(B A-1)of the minimum eigenvalue of the Hadamard product with an irreducible matrixBandA-1is given. And the theoretical proof of this paper is to improve the corresponding results given by Li hua in literature.

nonsingularMmatrix; Hadamard product; the minimum eigenvalue; estimation formula

O151.21

A

1009-9530（2016）05-0100-02

2016-04-21

李艳艳（1982－），女，文山学院数学学院讲师，硕士，主要从事矩阵理论及其应用方面的研究。