无线传感器网络K重覆盖节点部署与研究

◆张 帆

（国家新闻出版广电总局573台 北京 102209）

无线传感器网络K重覆盖节点部署与研究

◆张 帆

（国家新闻出版广电总局573台 北京 102209）

本文对无线传感器网络K重覆盖进行研究，运用Voronoi图实现K重覆盖，提出基于Voronoi图的K重覆盖节点自定位估算方案，通过仿真运行，验证了节点自定位估算方案的可靠性。

无线传感器网络；K重覆盖；Voronoi图；节点自定位估算

0 前言

k重覆盖就是当覆盖区内每个节点至少被一个以上的传感器节点监测到，即在坐标上，任意点x被两个或者两个以上的传感器节点覆盖住。Voronoi图，又称泰森多边形或Dirichlet 图，它是由一系列连接两个邻节点的直线的垂直平分线两两相交成的连续多边形组成。N 个在平面不同的点，在平面上按照最邻近原则划分；面上的所有点都与它的最近邻区域相关联。

1 运用Voronoi图实现k重覆盖

定理1：在Voronoi图中，节点is与同一图中任意一个顶点的距离都相同，公式可以表示为：

定义1：（Voronoi单元的完全覆盖）由定理1知，当一个Voronoi单元里每一个顶点都被图中的传感器节点is覆盖，则称就是Voronoi被完全覆盖，即：

定理2：根据定义1，假设覆盖区每一个Voronoi单元都被相应的传感器节点完全覆盖，那么称这种覆盖是一重覆盖。

图1 节点的边界覆盖

定理4：同时还反映出了节点与邻节点之间的关系，得出一种节点之间的最优距离关系，为接下来的一重覆盖和多重覆盖提供了论述依据。

在实际应用中，由于边界的的情况并不像覆盖区，所以通常都要考虑监测区域的边界的存在。假设覆盖区内传感器节点通过布尔感知模型覆盖感知边界，边界外并无传感器。如图1所示，传感器节点4s监测边界，并把边界上的1o点作为边界节点，节点4s得出1o的坐标位置。如图3b，节点4s与边界的交点分别命名为好，继而推出1o的坐标为。根据定理3，如果两个相邻节点直接的距离不大于，那么覆盖就会出现盲区，而我们假设1o是在边界的一个节点，所以节点4s到1o的距离也要不大于才能保证传感器网络在边界也能实现全覆盖。

但是如果不考虑边界的影响，假设为完美边界，那么覆盖区内每个节点的覆盖面积均为，那么二维平面中的节点密度为，由定理3知，为完全覆盖所需要的最少节点数，则

由定理3可知，一重覆盖时，网络中的最大覆盖面积实际上就是多个六边形的面积相加起来的面积，而每个节点的有效覆盖面积为，因此有效覆盖率即六边形的面积除以感知圆盘面积为。

在WSN的应用中，我们可以假设多重覆盖是由多个单重覆盖的子集集合而成，所以在k重覆盖中，网络的节点密度为k∂。在这里，本文提出虚拟感知半径vR的概念。运用vR可以将K重覆盖问题转换成单重覆盖问题，用公式表示为：

由上式子可知，节点的密度和覆盖重数的二次方成反比，可以退出虚拟感知半径跟覆盖重数K的关系，也即，由单重覆盖变成多重覆盖，k值变大，那么虚拟感知半径将变小，也就意味着节点密度变大。引入虚拟半径的方法可以将K重覆盖问题转化为单重覆盖问题，通过推导公式可以简化运算流程。

2 基于Voronoi图的K重覆盖节点自定位估算方案

2.1 条件设定

本文以的无线传感器网络由移动传感器节点组成，在覆盖区域的实现K重覆盖，并将无线传感器网络与本文所提出的节点自定位估算方案相结合，对以下覆盖区内的参数以及条件进行假设：

①覆盖区域为二维无障碍物的矩形平面空间；

②传感器节点具有移动能力，能事先通过某种定位方案，迅速对自身作出确的定位，并能准确移动至计算出的最佳位置；

③为了保证网络的连通性，规定传感器节点的通信半径CR大于或等于其感知半径sR的2倍；

④传感器节点通过布尔感知模型（1/0感知模型），在其感知半径内能监测网络的边界，并将边界视作邻居节点，假设其CR和均为零。

2.2 k重覆盖节点自定位估算方案

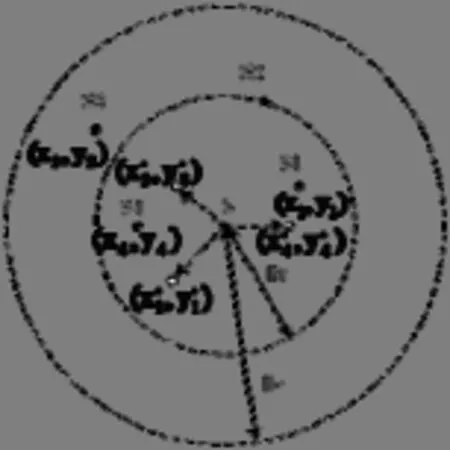
图2 邻居节点对传感器节点s的映射位置

根据应用Voronoi图实现K重覆盖的方法，我们可以按照自定位的的方案，将移动传感器移动到最合适的位置上来实现想要得到的覆盖，从一重覆盖知，虚拟半径变小，那么要实现K重覆盖，节点的距离从到，所以实际上移动传感器节点的感知半径不变只不过是节点之间的距离变小了，它们相互靠近，从使得覆盖重数增加。实现一重覆盖或者多重覆盖，事实上就是改变节点之间距离的变化——分散或者汇聚。

由上得知，把覆盖区内需要移动的节点S移动1S，且1S坐标为：

为了避免移动传感器节点移动过程中所有节点无序性和不必要的能量损失，确保自定位估算方案的收敛性，提高效率，需要设定一个无线传感器节点移动的限制值即门限参数为，也就是节点的原位置到优化位置之间的距离大于门限值时才被允许移动至新位置。如图3所示，在自定位方案中，为了避免无线传感器网络不同步而出现的不必要移动，必须在部署之初设置随机时间间隔，所有节点之间相互感应并收集邻节点之间的信息，并周期性地像邻节点发送信息。最后，每个节点通过计算与最优位置坐标的之间的距离并与门限值比较，决定节点是否需要移动。

在k重的无线传感器网络中，根据前文的推论和门限值的设定，每个节点可能移动的最大距离为，平均移动距离为。在自定位估算方案中，传感器节点在覆盖区内会由节点密度高的地方向密度低的地方移动来实现均匀分布，因此实现K重覆盖的复杂度为()On。实际上，在方案中，每一个传感器节点一般会发现个邻节点并且计算出最优位置。其时间复杂度为。

图3 k重覆盖的节点自定位估算方案

3 仿真结果及其分析

3.1 仿真参数

假设无线传感器网络的覆盖区域是一个无障碍物的二维平面的矩形区域，即为FLL=×（L为覆盖区域的边长），其中覆盖区内所有的节点都是采用布尔感知模型且都具有相同的感知半径和通信半径都相同，并随机的均匀分布在真个区域。使用到的参数如表1。

表1 仿真参数

3.2 仿真过程

（1）在100m×100m 的监测区域中随机投放k*|S|个节点（其中|S|由公式（3）算出，k可取1，2，3，4等）。在二维平面矩形区域随机部署传感器节点，节点的位置坐标可表示为：（2）得出随机投放传感器节点后的覆盖面积，并求出其覆盖率。（3）对于每一个传感器节点，定义位于其通信半径范围内的所有节点为邻节点，并按公式（6）求出邻节点的个数sn并按照公式计算出各邻节点的映射坐标，在根据公式（7）求出节点的最优位置。

（4）求出节点的原位置与最优位置坐标之间的距离temp，并将其与阈值比较大小，如果大于阈值，则节点就移动至最优位置。

（5）求出传感器节点经过移动部署后的覆盖面积，并求出覆盖率。

（6）增加传感器节点的数目，节点移动前和移动后均增加相同数目的节点数目，对比不同数目时候的节点覆盖率。

3.3 结果与分析

以下是k=1，2，3，4重覆盖的仿真过程的实现图片，S为覆盖的最少节点数目。

（1）k=1，S=56

图4 a 一重覆盖节点移动前后图

图4 b 一重覆盖覆盖面积图

（2）K=2，S=112

图5 a 二重覆盖节点移动前后图

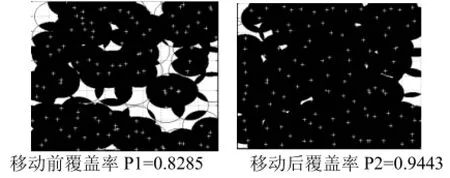
图5 b 二重覆盖节点移动前后的覆盖图

（3）K=3，S=168