基于混沌的数字图像加密算法研究

◆颜 俊

（长江大学电子信息学院电信系 湖北 434100）

基于混沌的数字图像加密算法研究

◆颜 俊

（长江大学电子信息学院电信系 湖北 434100）

当前伴随科技的不断发展，计算机网络与多媒体发展速度不断提升，这推动了数字图像的出现。保障数字图像信息安全已经成为互联网领域的重要任务。如今，在网络上已经越来越流行图像信息，但是由于一些图像信息会与个人隐私、商业秘密等有关联，甚至会关系到国家的安全，因此采取有效的保密传输措施极为重要。实践表明，混沌的普遍性较强，同时还伴随着一定的随机性，对系统参数以及初值具有极度的敏感性以及不可预测性等方面的优良特性，为此该方法能够为图像加密算法提供更加可靠的参考与依据。本文主要针对基于混沌的数字图像加密算法的算法研究思路和结果等进行分析和解读，其目的在于保障数字图像信息的安全。

数字图像；混沌；加密算法

1 对于Lorenz混沌系统图像加密方案的探究

要探究Lorenz混沌系统图像加密方案，便需要从以下几个方面着手，即：

1.1 恰当地选择混沌系统[1]

Lorenz为美国气象学家，他在研究大气湍流运动时，将大气运行的规律作为重要基础，建立起了一个较为简化的数学模型，三变量的自治常微分方程组[2]。运动方程可表示为：

其中σ、b、r代表着系统参数，并且当σ=10，b=8/3，r=28的时候，产生了奇怪吸引子[3]。Lorenz系统生成的实值混沌序列拥有三个方面的有点：第一点系统结构较低，维混沌系统相对比较复杂[4]，同时所产生的实值序列具有不可预测性；第二点加密序列的设计较为灵活，对于系统所输出的实值混沌序列需要进行相应的处理，经过处理以后能够产生相应的单变量或者多变量的组合加密混沌序列[5]；这与王英，郑德玲，鞠磊等在《基于Lorenz混沌系统的数字图像加密算法》一文中的观点相似。第三点加密算法的秘钥空间与低维混沌系统相比，将会高于低维混沌系统，同时系统的三个初始值与三个参数都能够被作为加密混沌序列的种子秘钥[6]。

1.2 维混沌实值序列的产生

Lorenz三维系统通常需要通过数值积分求得实值混沌序列，本文主要应用四阶龙格库塔数值积分的方式[7]，产生过程主要有以下几种，如：

第一可以对式（1）中的参数与初始条件进行设定，在这之中σ、b、r属于系统参数[8]；而x0，y0，z0属于系统初始值，h表示进行数值积分过程中的步长。

第二可以通过数值积分方式得到式（1）中离散数值解，该映射主要应用常微分方程组展开相应的描述，为此能够得到相应的离散实值序列，其数量为3个，即：x1，x2，...，xi；y1，y2，...，yi，...；z1，z2，...，zi，...。在加密期间可以通过其中任意一个序列来完成加密计算。

1.3 图像加密与解密的过程

本文研究所加密与解密的方案具体步骤表现如图1所示。

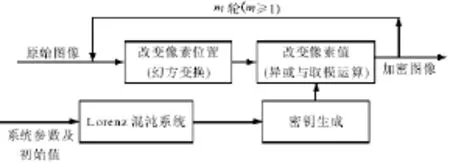
图1 加密与解密的方案步骤

第一需要通过标准幻方矩阵对图像采取像素位置置乱操作；第二需要将来两个离散的实值序列xi，yi，按照相应的方法转化为整数序列，φ（i）（1≤i≤N2，其中，N代表像素的宽度或者高度）[9]

其中trunc（.）代表截取小数部分运算，round（.）代表取整运算，mod N代表取模N运算。

2 仿真实验结果研究

对于一个密码系统而言，安全性是其中最为重要的问题。将理论与仿真实验结合，明确加密算法的安全性[10]。

本次试验中，为了能够保证评估算法的整体性能，工作人员应用了像素为256×256的灰度图像Lena图。将Lorenz系统的控制参数设为σ=10，b=8/3，r=28；将初始值设为0x=1.2833，而积分步长h此时值为0.001。经过试验与分析得知，应用该算法能够正确的加/解密文件，同时图像加密后的灰度直方图也会表现的更加均匀[11]。直方图如图2所示：

图2 原始图像和加密图像及其直方图

基于混沌的数值图像加密算法中，需要科学的对相邻像素的相关性进行分析，随机抽取两个相邻像素，并通过下列模型对相邻像素之间的关系进行表述。

3 安全性和性能的分析

（1）明确了混沌实值序列预处理，实验表明，理想的混沌序列应该具备几个方面的统计特性，如：分布均匀；与δ函数的自相相关；互相关性为零。可是实际上由公式（1）所产生的实值序列xi，yi， iz（i=1，2，...）具有较差的均匀分布特性，局部取值会呈现一定单调性，在应用期间很容易被破解，同时自相关与互相关的特性也欠缺合理性，没有达到理想的效果，这在一定程度上给序列的灵活性带来了限制[12]。为此，对xi，yi， iz做相应的预处理极为重要。例如：可以采用xi+yi序列，将“和”序列的整数部分去除[13]，从而为统一值域提供方便；另外，为了能够有效的提升序列取值的无规则性和整体分布的均匀性，在去整的基础之上，可以将小数点继续向后移3位，其处理过程如公式（2）。实践表明，经过预处理后所得到的混沌序列拥有较好的均匀分布特性，同时也包括随机统计特性与相关性[14]。这与柳娜在《基于混沌的数字图像加密算法的研究》一文中有着极为相似的观点。通过该种预处理方式，能够在一定程度上有效的提升序列的伪随机特性。

（2）对秘钥空间的分析。在本文加密算法中，Lorenz系统在迭代期间已经应用了IEEE 754浮点数标准[15]。设定x0值以后，便能够得出相应的秘钥空间，这增加了对图像信息的保护能力，蛮力攻击无法实现。

4 总结

伴随科技的不断发展，图像信息已经被人们所喜爱。但是由于图像信息在传输中会涉及到一些机密问题，因此保证图像信息的安全性极为重要。为了能够真正地做到这一点，应用相应的加密技术极为重要。本文主要立足于两点，通过试验的方式，首先对于Lorenz混沌系统图像加密方案展开了相应的探究，其次研究了仿真实验结果，最后对其安全性与性能进行了简单的分析。通过文中三点的整合，明确基于Lorenz三维混沌系统与标准幻方变换的数字图像加密算法在保障图像信息安全方面有着积极的意义，但是还需要在不断的研究与分析中完善。

[1]张鹏伟，张涛．对一个数字图像加密算法的安全性分析[J]．计算机工程与科学，2015．

[2]章秀君，吴志强，方正等．一种基于四维超混沌系统的数字图像加密算法[J]．计算机工程，2013．

[3]冯明库．基于小波变换的数字图像混沌加密算法[J]．电光与控制，2010．