散粒货物对敞车静侧压力的分布规律研究

赵方伟，付秀琴，张 弘，张澎湃，丛 韬，张关震，吴 斯

（中国铁道科学研究院 金属及化学研究所，北京100081）

散粒货物对敞车静侧压力的分布规律研究

赵方伟，付秀琴，张 弘，张澎湃，丛 韬，张关震，吴 斯

（中国铁道科学研究院 金属及化学研究所，北京100081）

为研究散粒货物对敞车的静侧压力分布规律，以满载散粒煤的C80B型敞车为研究对象，采用修正的D－P模型数值模拟散粒煤的本构模型，通过简化几何模型和有限元方法，建立了整车三维数值离散模型。在车体与散粒煤的接触面均设置柔柔接触，采用修正的硬接触关系模拟其法向接触行为，并引入“弹性滑移变形”模拟其切向摩擦行为。对车体静侧压力进行数值计算，并将结果与库仑土压力理论计算结果进行对比。结果表明：散粒煤中部沉降量最大，沉降量沿装货高度呈非线性分布；侧压力沿敞车墙高非线性分布，且在顶部位置不为零；散粒煤对敞车的侧压力沿车长和车宽方向非均匀分布，呈非线性分布。

敞车；散粒货物；D－P模型；数值模拟；侧压力

在铁路运输的货物中，煤、矿石、矿材、粮食等以散装形式运送的颗粒状货物占总的货物发送量的七成以上。随着铁路货运的提速和重载化，散粒货物对敞车的作用问题变得日益突出。针对散粒货物对敞车的作用问题，尤其对端、侧墙的压力问题，国内外学者做了大量研究。

美国铁道学会AAR标准［1］按Rankine土压力公式计算散体作用于敞车端、侧墙的压力，认为其压力分布是线性三角形分布。我国TB／T 1335－1996《铁道车辆强度设计及试验鉴定规范》［2］中规定的散粒煤对敞车端、侧墙的计算方法是基于二维计算模型，认为散粒煤对端、侧墙的压力沿车长和车宽均匀分布。近些年，随着CAE技术的发展，散粒煤对敞车侧压力的研究引入了新的手段和方法。文献［3］在有限元软件中建立二维有限元模型，以M－C屈服准则模拟散粒货物塑性模型，研究了散体对敞车端墙的作用规律。文献［4］采用二维模型分析了极限状态时，散粒煤对车体端墙的侧压力分布。实践证明，二维计算模型不能反映真实情况。文献［5］建立了三维有限元计算模型，但采用的是集中质量法，以刚性杆单元模拟散粒货物对敞车的作用情况，无法真实的模拟散粒货物的流动性，误差较大。文献［6］考虑了端、侧墙加强横带的影响，以C70型敞车车体真实结构为研究对象，建立三维有限元模型，分析了散粒煤对车体端、侧墙的侧压力，但对于结构不同的敞车车体而言，不具有普遍规律性。

为了更准确的模拟散粒货物沿端、侧墙两个方向的侧压力分布规律，以C80B型专用敞车为原型，简化并建立整车三维数值模型，对其进行数值仿真计算。散粒货物选取煤作为分析对象，采用修正的D－P准则，对车体端、侧墙静侧压力进行数值模拟，分析散粒货物对敞车静侧压力的分布规律。研究的成果可以为我国运煤敞车端、侧墙压力校核标准的改进和完善提供理论依据，也可以为车辆的结构设计优化提供参考。

1 数值模型

1.1 散粒煤本构模型

根据土力学理论，散粒煤属于典型的颗粒状松散货物，本构模型一般选择M-C模型、D－P模型和修正的D－P模型。

（1）Mohr-Coulomb（M－C）理想弹塑性模型

Coulomb在土的摩擦试验、压剪试验和三轴试验的基础上，于1773年提出了库仑破坏准则，认为当土体某平面上剪应力达到某一特定值时，便进入屈服［7］。其准则方程形式一般为

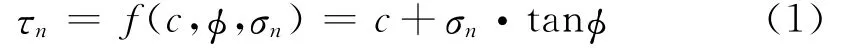
式中c为土的黏聚力，φ为土的内摩擦角，σn为屈服面上的正应力。该方程通过试验确定。

在π平面上的屈服曲线为一封闭的非正六边形。现在，M－C准则仍被广泛应用，该准则在π平面上的拉、压轴相等时即为广义Tresca准则。M－C准则比较符合试验，但是它的缺点在于三维应力空间中的屈服面存在角点奇异性，且没有考虑中间主应力σ2的影响。

（2）Drucker-Prager（D－P）模型

1952年Drucker和Prager首先把不考虑中间主应力σ2影响的Coulomb屈服准则与不考虑净水压力影响的Mises准则联系在一起，提出广义Mises理想塑性模型，即D－P模型［8］。D－P模型的屈服面方程为

D－P屈服函数所表示的屈服面在π平面上是一个圆，更适合数值计算。但是作为近似计算，D－P模型仍被广泛应用。

（3）扩展的Drucker-Prager（D－P）模型

该模型可以用来模拟摩擦材料，典型的是粒状岩土材料及表现压力相关的屈服材料；还可以用来模拟抗压屈服强度大于抗拉屈服强度的材料，且容许材料等向硬化或软化。修正的D－P模型屈服面方程为

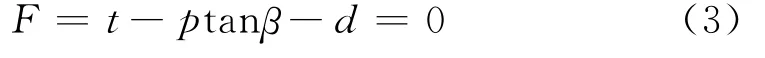
式中t＝q／2［1＋1／k－（1－k）（r／q）3］，q为偏应力，k为三轴拉伸强度与三轴压缩强度之比，反映了中间主应力σ2对屈服的影响，r为第3偏应力不变量，p为平均应力，β为材料的内摩擦角，d为材料的粘聚力。

修正的D－P模型屈服面在π面上的图形为光滑过渡曲线，且考虑了平均主应力的影响。

由于在铁路运输过程中，散粒煤主要承受压应力，受压屈服强度远大于受拉屈服强度，因此，选取修正的D－P模型来描述散粒煤本构模型更合适。散粒煤本构模型参数如表1所示。

表1 散粒煤本构模型参数

1.2 有限元模型

C80B专用敞车车体主要是由钢板焊接而成，车体内部长、宽、高分别为10 550 mm，2 976 mm，2 600 mm。为研究散粒煤对敞车侧压力的规律，将C80B敞车简化为没有顶面的立方体薄板结构，单元类型选取板壳单元Shell63，网格划分的精度直接关系到有限元计算的准确性，采用等尺寸单元进行划分。通过网格离散建立仿真离散模型，如图1所示。根据实际情况，仅在敞车底板处设置全约束边界条件。车体为钢结构，材料参数设置为：密度7.8×10－9t／mm3，弹性模量2.1×105 MPa，泊松比0.3。

图1 车体仿真离散模型

不考虑颗粒物性参数、粒径形状对结果的影响，只研究整个散体所表现出来的属性，根据连续介质理论，把散粒介质近似为连续介质［9］。因此，采用实体单元模拟散粒煤，单元类型选取Solid45六面体单元。设定散粒煤的装货高度与敞车车体的内高相同。散粒煤仿真离散模型见图2。计算载荷为车体与散粒煤的自重。

图2 散粒煤仿真离散模型

1.3 接触面力学模型

在敞车车体底面、端墙和侧墙均设置接触对，接触类型选择柔柔接触，刚度较大的车体表面作为接触主面，散粒煤表面为从面［10］。在车体与散粒煤的三维建模分析中采用面面接触方法模拟车体与散粒煤的接触行为。

（1）接触面的法向模型

对于接触问题，车体与散粒煤只有在压紧状态时才传递法向应力p，存在间隙时不传递法向压力，这种法向行为被称为硬接触［11］。硬接触在计算中限制了可能发生的穿透现象，但当接触条件从间隙为正到间隙为零时，接触压力会发生剧烈的变化，有时使得接触计算很难收敛。

根据岩土工程理论，认为车体与散粒煤接触面具有黏聚力，在脱开之前能承受一定的拉力，这时可采用修正硬接触关系。为保证接触计算收敛，可以指定一个能承受的拉力pmax，在拉力超过该值后才认为接触面脱开，接触压力变为零；也可以指定一个适当的过盈量hmax，当过盈量超过hmax后才认为接触面从脱开转为闭合。

（2）接触面的摩擦模型

当接触面处于闭合状态时，接触面可以传递摩擦力。若摩擦力小于某一极限值τcrit时，接触面处于黏结状态；若摩擦力大于τcrit之后，接触面开始出现相对滑动变形，此时处于滑移状态［12］。在理想状况下，车体与散粒煤接触面在滑移状态之前没有剪切变形，在仿真计算时容易导致不收敛。需要对计算模型进行修正，通过引入“弹性滑移变形”，允许接触表面黏结在一起时发生少量相对滑移变形。根据车体与散粒煤接触面上单元的长度确定弹性滑移变形，一般设置为单元典型长度的0.5%，然后选择罚摩擦方法中的刚度进行计算。

2 位移响应分析

2.1 散粒煤位移响应

散粒煤的垂向位移响应结果，如图3所示。分别选取散粒煤端墙中部、侧墙中部和端侧墙连接处3个位置的垂向一排节点，以散粒煤顶部为起点，描绘垂向位移响应曲线，如图4所示。

图3 散粒煤垂向位移响应云图

图4 散粒煤垂向位移曲线

由图3可见，在重力作用下散粒煤发生了沉降，散粒煤中部垂向位移最大，最大值为6.618 mm。由于散粒煤与车体端、侧墙摩擦力的作用，靠近车体端、侧墙的散粒煤沉降量小于内部。由图4可以看出，散粒煤在端、侧墙部位的垂向位移随着装货高度的增加而逐渐减小，且呈非线性递减。同一装货高度下，侧墙垂向位移大于端墙垂向位移，端侧墙连接处垂向位移最小。随着装货高度的减小，端、侧墙部位及其连接处的垂向位移差值逐渐变小，说明越靠近底部沉降逐渐变得均匀。原因是底部散粒煤所受的压力大大超出外摩擦力，使得散体与敞车摩擦力对散体的影响逐渐减弱。

2.2 车体位移响应

散粒煤作为散粒状介质具有流动性，其侧压力作用在车体上使车体发生位移变化，根据土力学中挡土墙侧压力理论，车体的位移变化又会反过来影响散粒煤的侧压力［13］，因此，为分析散粒煤对车体端、侧墙的侧压力情况，提取计算结果中车体纵向和横向位移响应，分别如图5～图6所示。

图5 车体纵向位移响应云图

图6 车体横向位移响应云图

在散体侧压力的影响下，敞车端墙的最大纵向位移为0.028 36 mm，出现在敞车端墙顶部位置。端墙靠近底部的中间位置出现与顶部反方向的变形，这一现象的出现是由于散粒煤在重力作用下发生沉降，导致作用中心位置下移。敞车侧墙的最大横向位移为0.500 2 mm，出现在敞车侧墙靠近中间位置的顶部。

3 接触侧压力分析

以散粒煤顶部为起点，描绘散粒煤端墙中部、侧墙中部测点的压力分布曲线，并与经典库仑理论计算结果进行对比，如图7所示。

图7 接触侧压力曲线

根据土力学理论，端、侧墙的位移直接影响侧压力的大小，如果端、侧墙位移方向与散粒煤作用方向相同，则会出现压力松弛现象，导致侧压力减小；如果端、侧墙位移方向与散粒煤作用方向相反，则会出现压力缩紧现象，导致侧压力增大；列车静态工况下，端、侧墙与散粒煤之间的侧压力属于挡土墙“被动土压力”，受散粒煤的压力，端、侧墙有向外的位移，与散粒煤作用方向相同，所以侧压力会减小。减小的程度与位移大小有关，位移大则减小的幅度越大，反之，则减小的幅度越小。

由图7可以看出：（1）散粒煤对敞车端、侧墙的侧压力沿墙高均呈非线性分布规律，且比库仑理论计算结果略小，说明基于库仑理论计算的车体端、侧墙侧压力存在一定误差；（2）散粒煤在车体顶点处的侧压力不为零，约为0.14 k Pa；（3）在墙高的中上部分，端墙上的侧压力值要大于侧墙上的侧压力值，原因是在侧压力的作用下车体侧墙顶部相对于端墙顶部发生了更大变形。底部附近，侧墙上的侧压力值更大，原因是底部位置端墙变形相对更大；（4）在墙高的中部区域，近似呈线性分布，侧压力随着深度的增加而增大；在墙高的下部分，仿真的结果与库仑理论计算的结果迥异，侧压力值出现压力松弛的现象。

为进一步分析同一高度散粒煤对敞车端、侧墙的压力分布规律，沿端墙—侧墙水平方向选取等间距测点，描绘等高度侧压力曲线，如图8所示。

由图8可知，散粒煤对敞车的侧压力沿车长和车宽方向非均匀分布，且呈非线性分布。对于最为关注的车体端墙，侧压力沿车高呈非线性分布，且在顶部位置不为零；在墙高的中部区域，近似呈线性分布，侧压力随着深度的增加而增大；在底部出现压力松弛现象（如图5～图6所示），最大侧压力出现在车体底部偏上位置。

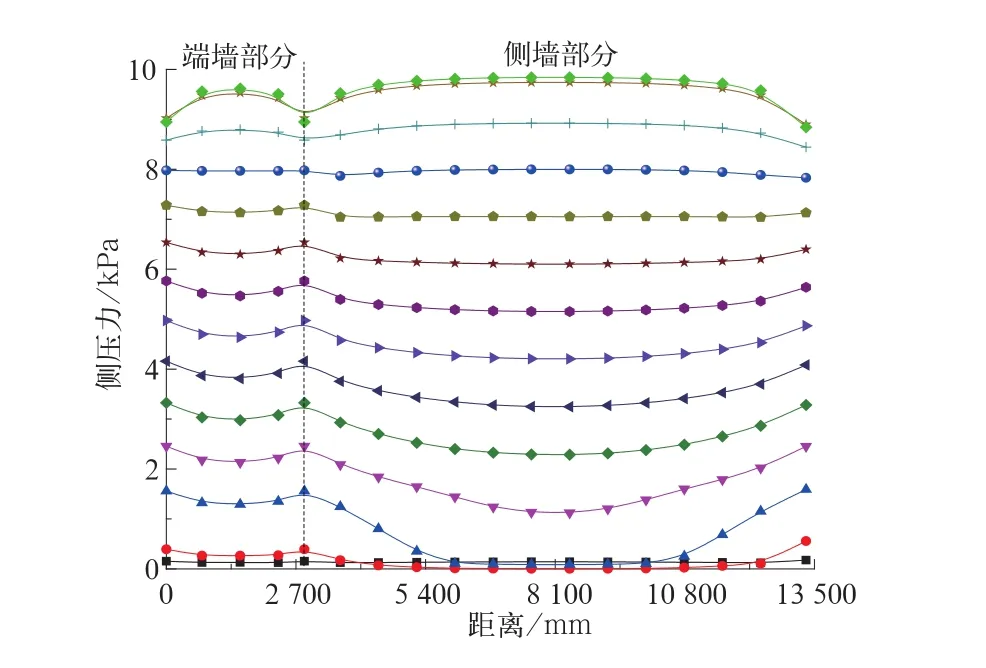
图8 等高度接触侧压力分布曲线

4 结 论

（1）简化C80B型敞车模型，提出采用修正的D－P模型描述散粒煤的本构模型，考虑车体与散粒煤之间的接触关系，实现了散粒煤对敞车车体侧压力的三维仿真模拟。该方法可以为进一步研究其他载重车型提供参考。（2）在重力作用下散粒煤发生不均匀沉降，中部沉降量最大，沿墙高沉降量呈非线性分布。敞车端墙的最大纵向位移出现在敞车端墙顶部位置；侧墙的最大横向位移出现在敞车侧墙靠近中部位置的顶部。（3）通过对比分析端墙与侧墙的侧压力分布曲线发现，两者的侧压力值大小并不相同，在墙高中上部分，端墙上的侧压力值要大于侧墙上的侧压力值；底部附近，

侧墙上的侧压力值更大。因此，在对车体侧压力校核时，应分别校核端、侧墙侧压力。（4）散粒煤对敞车的侧压力沿车长和车宽方向均呈非线性、不均匀分布，说明采用二维模型得到的侧压力分布结果不准确。

［1］ AAR Manual and Standards［S］.America：Association of American Railoads，1999.

［2］ TB／T 1335－1996铁道车辆强度设计及试验鉴定规范［S］.北京：中华人民共和国铁道部，1996.

［3］ 何华.铁路货车的散体货物_流体货物动压力研究［D］.长沙：中南大学，2008.

［4］ 曾祥坤，田红旗.散粒货物对铁路敞车端墙侧压力研究［J］.铁道学报，2007，29（4）：32-37.

［5］ 杨爱国，张志强，杨江天.基于有限元建模的敞车轻量化设计［J］.中国铁道科学，2007，28（3）：79-83.

［6］ 王斌杰，赵方伟，李强.散粒煤对敞车静压力的三维有限元模拟［J］.铁道学报，2016，38（2）：17-22.

［7］ Vidal P，Gallego E，Guaitac M，et al.Finite element analysis under different boundary conditions of the filling of cylindrical steel silos having an eccentric hopper［J］.Journal of Constructional Steel Research，2008，（64）：480-492.

［8］ Rotter J M，Hoist F G，Ooi J Y，et a1.Silo pressures predictions using discrete-element and finite element analyses［J］.Philosophical Transaction Mathematical，Physical and Engineering Sciences，Series A，1998，356：2685-2712.

［9］ Hubner A，Teng J G，Saal H.Buckling behaviour of large steel cylinders with patterned welds［J］.International Journal of Pressure Vessels and Piping，2006，（83）：13-26.

［10］ Vidala P，Gallegob E，Guaitac M，et al.Finite element analysis under different boundary conditions of the filling of cylindrical steel silos having an eccentric hopper［J］.Journal of Constructional Steel Research，2008，64：480-492.

［11］ 朱向荣，王金昌.ABAQUS软件中部分土模型简介及其工程应用［J］.岩土力学，2004，25：144-148.

［12］ Juan A，Moran J M，Guerra M I，et a1.Establishing stress state of cylindrical metal silos using finite element method：comparison with ENV 1 993［J］.Thin-Walled Structures，2006，44：1192-1200.

［13］ OOI J Y，SHE K M.Finite Element Analysis of Wall Pressure in Imperfect Silos［J］.Solid Structures，1997，34（16）：2065-2072.

Static Lateral Pressure Distribution Study of Granular Cargo on Gondola Car

ZHAO Fangwei，FU Xiuqin，ZHANG Hong，ZHANG Pengpai，CONG Tao，ZHANG Guanzhen，WU Si
（Metals＆Chemistry Research Institute，China Academy of Railway Sciences，Beijing 100081，China）

In order to study the static lateral pressure distribution of granular cargo on gondola car，C80B gondola car full of granular coal is regarded as the research object.Revised D－P model is adopted to simulate the constitutive model of granular coal.Through the simplified geometric model and finite element method，3－D numerical discrete model of car body is established.Flexible-flexible contact type is set between car body and granular coal.The modified hard contact is used to simulate the contact behavior.The elastic slip deformation is introduced to simulate the tangential friction behavior.Static lateral pressure on the gondola car body is simulated.The results are compared with the Coulomb pressure theory.It shows that the granular coal settled under gravity，and central vertical displacement is largest.Along the loading height，the distribution of settlement is nonlinear.The lateral pressure distribution along wall height of gondola car is nonlinear，and the value at the top is not zero.The lateral pressure along the length and width direction of gondola car is non-uniform distribution，and distribution is nonlinear.

gondola car；granular cargo；D－P model；numerical simulation；lateral pressure

U272.2

A

10.3969／j.issn.1008－7842.2016.06.11

1008－7842（2016）06－0042－04

7—）男，助理研究员（

2016－07－15）