任务呈现方式、双任务反应顺序影响算术估算策略选择与执行*

艾继如 张红段 司继伟 卢 淳 张堂正

(山东师范大学心理学院, 济南 250358)

1 引言

在算术计算任务中, 个体的行为依赖于所使用的策略(Uittenhove & Lemaire, 2012)。策略是完成较高水平目标或任务的一个或一系列程序(司继伟,徐艳丽, 封洪敏, 许晓华, 周超, 2014)。策略运用包括策略分布、策略选择和策略执行, 是个体在问题解决过程中如何选择策略以及如何使用特定策略去解决问题的过程(Lemaire & Lecacheur, 2011)。有研究显示, 无论是两位数(36×23)还是三位数(429+287)的算术估算问题, 个体在上调策略(将两个加数都向上调整到最接近的整十数然后相加, 如46+78, 上调策略：50+80=130)中的反应时间明显长于下调策略(将两个加数的个位数字舍去, 变成整十数, 然后相加, 如43+69, 下调策略：40+60=100),且正确率低于下调策略(Lemaire & Lecacheur, 2002)。现有研究指出算术策略的运用会受到各种因素的影响, 如情境特征、个体特征、文化差异(Imbo &LeFevre, 2009, 2011)、前一问题的策略使用(Ardiale &Lemaire, 2012; Lemaire & Lecacheur, 2010; Schneider &Anderson, 2010 )等。

中央执行作为工作记忆中的核心成分, 是对当前信息加工的管理、监督和控制系统(Baddley & Hitch,1974), 对个体的算术任务表现有着重要影响。Imbo和Vandierendonck (2007)发现被试完成心算任务的策略执行表现会受到中央执行负荷的影响, 无负荷实验条件下的反应时间短, 正确率高。国内的近期研究也发现无负荷实验条件下, 个体的策略选择适应性表现最好(司继伟, 杨佳, 贾国敬, 周超, 2012)。个体的策略运用过程易受中央执行成分的制约(Hodzik & Lemaire, 2011), 而双任务协调属于中央执行的重要成分, 它体现了个体合理分配注意力、保证两个任务顺利完成的能力(彭华茂, 张凌, 申继亮,2009)。可见个体的策略运用可能会在一定程度上受到双任务协调能力的制约。

与单独执行每个任务相比, 个体同时从事两个任务的反应时间往往更长、正确率往往更低(Schubert,Fischer, & Stelzel, 2008; Szameitat, Lepsien, von Cramon,Sterr, & Schubert, 2006)。双任务协调的存在促使许多研究者寻找影响双任务协调的因素。有研究发现,当前后两个实验中任务呈现顺序不同时, 被试需付出更多的努力, 表现为外侧前额叶激活程度增加(Szameitat et al., 2006)。Leonhard和Ulrich (2011)使用视觉任务(加号和减号辨别任务)和听觉任务(声音左右辨别)作为双任务, 结果发现刺激呈现顺序和准备对中央加工阶段具有重要作用。关于双任务协调的理论模型主要有3种：反应选择瓶颈模型认为个体信息加工中存在一个瓶颈, 在瓶颈阶段个体一次只能加工一个任务; 而中枢能量共享模型主张个体的中枢反应选择对信息是平行加工的, 总认知资源的有限导致分到每个任务上的资源有限, 从而导致两个任务上的反应时延长; 执行控制交互作用模型则着眼于个体对两个任务的协调控制过程,强调个体根据不同情境灵活的选择不同策略。那么在估算相关双任务中, 被试的表现用哪一种理论来解释更加恰当呢？这也是我们要探究的问题。

选择/无选法是Siegler和Lemaire (1997)发展起来的研究策略选择的新兴范式, 能对策略选择进行无偏估计。该范式包括两种实验条件：有选条件下,被试可自由选择想要使用的策略解决每个问题：无选条件下,被试必须使用给定策略解决所有问题。无选条件下的策略数目和有选条件下被试的可选策略数目相等(张红段, 王玉璇, 胡冬梅, 李红霞, 司继伟, 2015)。本研究中的策略运用条件主要有：最佳选择(有选条件)、无选上调、无选下调。此外, 当估算题目的数字消失时, 被试需要在头脑中保持题目信息, 这就会占用大量的工作记忆资源从而导致被试的策略运用受到一定程度的影响。

本研究将以算术估算为突破口, 通过设置不同的双任务情境考察个体双任务协调能力, 我们推测估算题目的数字消失与否会对双任务表现产生影响。估算题目的数字消失的条件下, 个体在两个任务上的反应时更长, 错误率更高。通过对不同双任务情境下策略运用表现变化的考察, 能揭示个体究竟如何根据任务情境变化, 灵活地选择并执行算术策略, 有助于探测个体算术加工的内在机制以及探讨双任务协调理论模型对当前任务中被试表现的解释力, 从而为揭示工作记忆与策略运用的灵活性、适应性之间的内在联系提供一定证据支持。

2 实验1

2.1 目的与假设

2.1.1 实验目的

通过设置两个不同的双任务情境(估算题目的数字消失与不消失), 对被试双任务协调的行为表现进行考察, 分析任务呈现方式、双任务反应顺序对个体的算术策略选择与执行的影响。

2.1.2 研究假设

(1)估算题目的数字消失时, 个体完成两个任务需要更多的认知资源, 两个任务都回答正确的比例有所下降; (2)估算题目的数字消失条件对个体策略选择的影响更大, 为避免资源的耗竭, 个体可能会倾向于选择较简单的策略; (3)上调策略的反应时间长, 错误率高, 策略执行中, 估算题目的数字消失的条件对上调策略的影响更大。

2.2 方法

2.2.1 被试

随机选择在校大学生31人, 男生17人, 女生14人, 平均年龄20.85岁。

2.2.2 实验设计

采用2(估算题目的数字消失与否：消失, 不消失)×3(策略运用条件：最佳选择, 无选上调, 无选下调)被试内实验设计, 因变量为被试两个任务的反应时和正确率。字母任务中, 如果被试输入的答案等于两个字母代表的数字相加之和则判定为正确。估算任务中：无选条件下, 被试输入的估算答案等于按照相应的方法将两个运算数调整到整十数后相加的结果(无选上调：46+78, 被试输入130, 则判定为正确; 无选下调：46+78, 被试输入110则判定为正确), 最佳条件下, 被试对上调题目选择了上调策略, 对下调题目选择了下调策略(上调题目：46+78, 被试输入130, 则表明被试选对了策略并得到了更精确的估算结果; 下调题目34+52, 被试输入80, 则表明被试选对了策略到了更精确的估算结果)判定为正确。

2.2.3 实验材料

两位数加法估算任务(主任务)：120道题目, 分3个区组, 最佳选择条件下48道题目, 无选上调和无选下调条件下各36道题目。3个区组的精确计算的正确答案平均值分别为131.52, 131.11, 131.44。题目全部为混合题目(即一个加数的个位数字大于5,另一个加数的个位数字小于5), 和为三位数。若两个加数个位数字相加和大于10, 则为上调题, 若两个加数个位数字相加和小于10, 则为下调题。每个区组中, 上、下调题目各占一半。每个区组又分成两个小组：估算题目的数字消失组与不消失组, 两个小组内上、下调题目亦各占一半, 两个加数中大数在前的题目占所有题目的1/2, 正确答案和估算值之间的差异在两个小组之间进行匹配, 最佳选择条件下为8.13, 8.33; 无选上调条件下为10, 10.56; 无选下调条件下为10.17, 9.94。该任务已在前期研究中得到使用(司继伟等, 2012; 杨佳, 2012)。关于估算题目的选择, 主要对以下几方面进行了控制：1)个位数字中没有0或5; 2)两个加数的十位或个位数字不能重复; 3)每个加数个位和十位数字不能重复; 4)两个加数不能调换位置重新使用(Campbell, 2005)。

字母替代任务(次任务)：改编自司继伟等(2012)研究中的字母任务。与之前不同的是, 本研究并非要求被试将字母排序, 而是要求他们对字母所代表的数字相加。A、B、C、D 四个字母分别代表着数字1、2、3、4, 每两个字母组成一对, 共12对, 分别为AB AC AD BA BC BD CA CB CD DA DB DC。实验中, 两个字母连续快速呈现, 当第二个字母消失后, 被试需输入两个字母所代表的数字相加的和,若第一个字母为A, 第二个字母为B, 被试应该输入答案3。

2.2.4 实验程序

先向被试介绍两种任务, 告知被试先反应估算任务, 再反应字母任务, 且两个任务同等重要, 对每个任务都要既快又准地做出反应。主试以纸笔形式给被试呈现2到3道估算题目, 给被试讲明白上调策略和下调策略两种估算策略, 强调最佳选择条件下要选用会得到更加接近准确答案的估算策略。确保被试明白后再让被试开始实验。开始实验时,两个任务同时呈现, 分作3个区组：无选上调、无选下调和最佳选择。每个区组开始有10道练习试次, 给予被试正误反馈。3个区组中, 一半题目中估算题目的数字呈现固定的时间(策略无选条件下1700 ms, 策略选择条件下2700 ms)后消失, 一半题目中估算题目的数字则一直在屏幕上直到被试将两个任务都完成后消失。这两种情况的出现顺序随机化。字母任务的反应规则在3个区组中一致。无选条件下, 12对字母对应36道算术题, 将算术题随机分成12组, 每组3道题目, 和字母对相匹配;最佳选择条件下, 将算术题随机分成12组, 每组4道题目和字母对相匹配。所有被试均按照先无选下调再无选上调再最佳选择的顺序完成实验, 被试每完成一个区组, 休息3 min。

实验开始后, 屏幕中央先出现指导语, 被试理解后, 按空格键消失, 之后出现一个“+”, 500 ms之后, “+”消失, 屏幕上出现一道算术题, 算术题上方有3个小方框, 其中一个方框中有一个字母, 持续500 ms (由于策略选择所需时间较多, 为避免因刺激呈现时间太短给实验带来的干扰, 在最佳策略选择条件下, 刺激呈现时间为1000 ms)后, 字母消失,算术题不变, 700 ms之后(为了消除视觉后像的影响), 算术题上方的其他方框内, 出现另一字母, 持续500 ms (最佳选择条件下为1000 ms)。之后, 实验分两种情况, 或者字母和估算题目的数字都消失,出现一个黑屏, 被试先输入算术题答案, 再输入字母答案(见图1); 或者字母消失, 估算题目的数字不消失, 被试同样先输入算术题答案, 再输入字母答案(见图2)。从字母消失到被试输入答案的这段时间为被试的估算反应时, 由计算机记录。

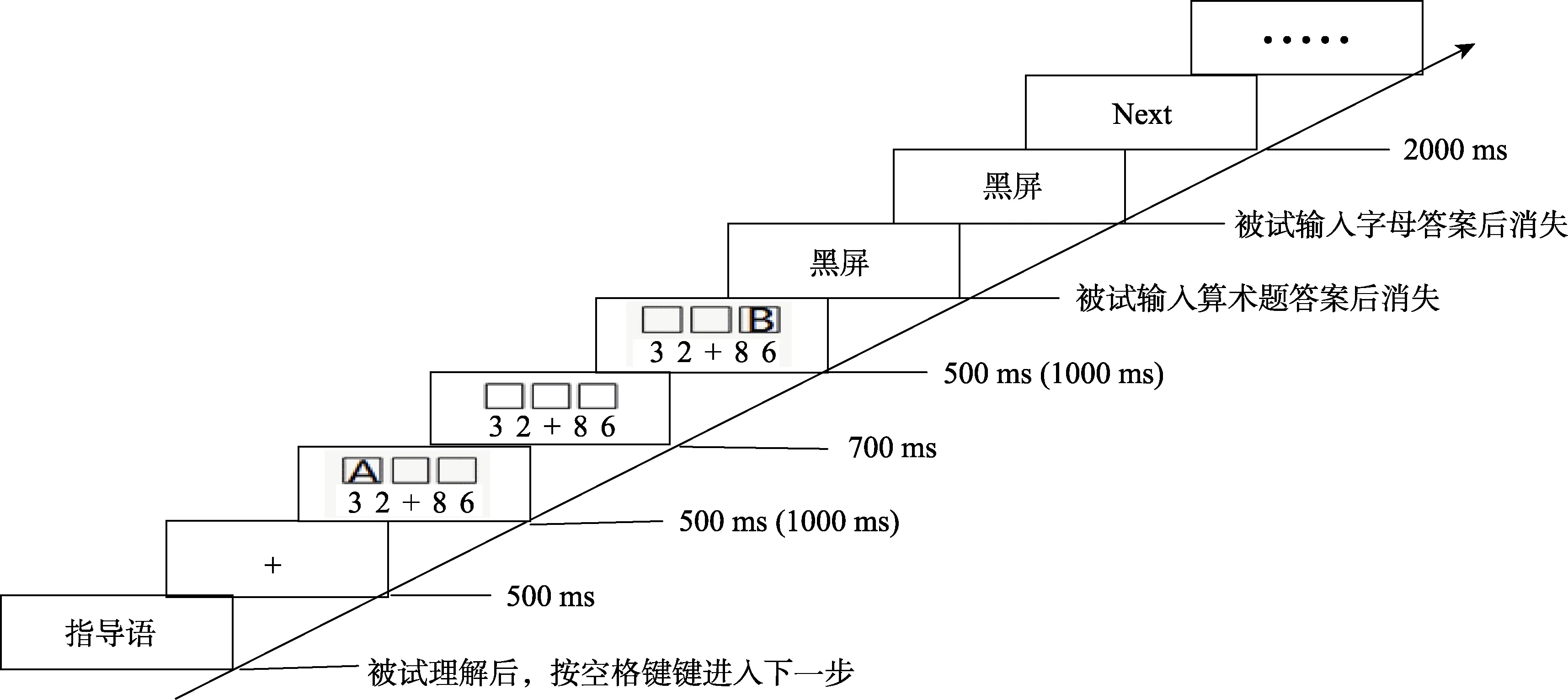
图1 估算题目的数字消失情境下的双任务操作流程

图2 估算题目的数字不消失情境下的双任务操作流程图

2.2.5 数据处理

采用SPSS 16.0和Excel 2003对数据进行统计分析。

2.3 结果

数据分析开始之前, 剔除正负3个标准差之外的数据和通过茎叶图选出来的极端数据, 最终策略选择条件下的有效被试有29人, 策略执行条件下的有效被试有30人。

2.3.1 个体双任务协调的结果

为考察在3个实验条件下, 估算题目的数字消失与否是否会影响到被试的双任务表现, 以被试两个任务都回答正确(同一试次中, 字母相加任务正确并且估算任务正确)的比率(见表1)作为因变量,进行配对样本t检验, 以确定所设置的两个双任务情境的有效性。对3种条件下被试两个任务都回答正确的比率进行配对样本t检验, 结果显示：最佳选择条件下,t(28)=3.95,p< 0.001; 无选上调条件下,t(29)=3.30,p< 0.01; 无选下调条件下,t(29)=2.81,p< 0.01。可见, 估算题目的数字消失与否的确影响了被试双任务表现。在算术题消失情况下,被试的双任务表现更差, 两个任务都回答正确的比例更低, 说明所设置的两个双任务情境是有明显区别的。并且由表1可知, 3种条件下, 被试对两个任务都回答正确的比例最低的在59%左右, 这说明被试在次任务上的正确率最低的也在59%左右, 说明被试的确按照要求进行了双任务加工, 字母任务起到了干扰作用。

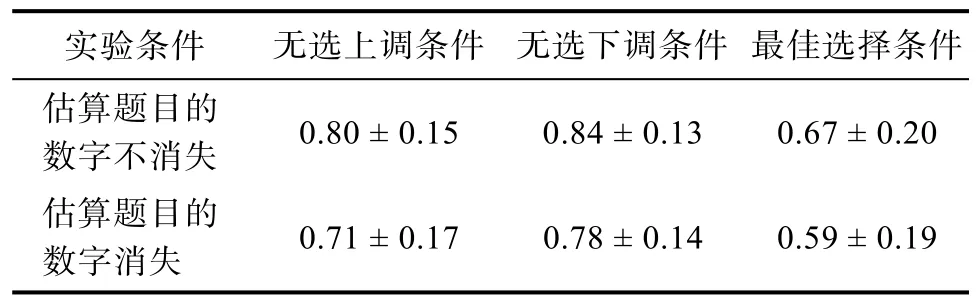
表1 在3个实验条件下被试对两个任务都回答正确的比例(M ± SD)

2.3.2 不同双任务情境对策略运用的影响

分析估算题目的数字消失与否对个体估算策略运用的影响, 主要考虑策略执行和策略选择两方面。

策略执行时被试要按指定策略解决问题, 无需根据个位数大小进行判断选择, 个位数的大小对这一过程的影响很小。而策略选择时, 被试可能根据个位数的大小选择一种更合理的策略, 显然这一过程会影响到被试的反应。故在分析策略执行时, 我们没有把题目类型(上调题、下调题)作为自变量进行统计处理。个体在两种无选条件下的估算反应时和正确率见表2。以反应时和正确率为因变量, 进行2(策略执行条件：无选上调, 无选下调)×2(估算题目的数字消失与否：消失, 不消失)重复测量方差分析。结果发现：策略执行条件在反应时上主效应显著,F(1,29)=60.53,p< 0.001, η²=0.676, 上调条件的反应时显著长于下调条件。估算题目的数字消失与否在正确率上主效应显著,F(1,29)=6.23,p<0.05, η²=0.177, 算术题消失的情况下, 错误率更高, 其他主效应和交互效应均不显著。

策略选择条件下, 个体策略选择正确的比率(上调题目选择上调策略, 下调题目选择下调策略)结果见表3。对被试策略选择正确的比率进行2(题目类型：上调题目、下调题目)×2(估算题目的数字消失与否：消失, 不消失)重复测量方差分析。结果显示：估算题目的数字消失与否主效应显著,F(1,28)=4.71,p< 0.05, η²=0.144, 估算题目的数字不消失,个体更容易选择最佳策略; 题目类型主效应不显著F(1,28)=3.76,p=0.06, η²=0.118; 两者交互作用不显著F(1,28)=0.07,p=0.80。

表2 不同策略执行条件下被试的正确率与反应时(M ± SD)

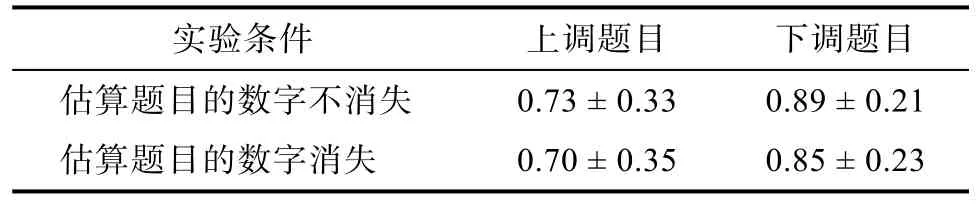
表3 个体在最佳策略选择条件下策略选择正确率(M ± SD)

2.4 讨论

该实验结果显示, 不同的双任务呈现情境会对个体的双任务表现产生明显影响。估算题目的数字消失时, 个体在两个任务上的表现差, 说明不同双任务情境下, 个体可能需要开展不同的认知努力,所消耗的认知资源也有差异。本研究中, 估算题目的数字不消失, 允许个体将较多认知资源集中在字母任务上, 但当估算题目的数字消失时, 个体就必须在头脑中同时存贮并加工两个任务, 就可能会导致两个任务在反应选择阶段的重叠时间有所延长,加之估算任务和字母替代任务都涉及加法运算, 两个任务之间就会产生干扰(Schubert et al., 2008), 从而导致表现相对较差。估算题目的数字消失对几种策略条件的影响都达到显著水平, 说明任务呈现方式确实影响到了算术估算策略的选择与执行。这也说明, 用执行控制交互作用理论来解释当前任务中被试的双任务表现更为合理, 因为被试似乎根据情境的变化调整了双任务协调策略。

有研究证实两个任务的难度不匹配时, 任务1难度比较大时, 个体便会优先加工任务2 (Leonhard,Fernández, Ulrich, & Miller, 2011)。本实验中, 要求被试先反应估算任务, 后反应字母任务, 那么个体是否就会按要求优先加工估算任务, 在估算任务中分配更多资源呢？鉴于前人研究中发现了反应顺序的差异会影响个体对两个任务的表现(Leonhard &Ulrich, 2011), 并且Sigman和Dehaene (2006)认为认知资源由任务1转向任务2时, 转换过程中会出现转换代价。因此有必要考察当要求个体后反应估算任务时, 其策略运用表现是否会出现变化。因此我们进一步进行了实验2。

3 实验2

3.1 目的与假设

3.1.1 研究目的

考察当个体先反应字母任务, 后反应算术任务时, 估算题目的数字消失与否对个体的算术策略选择与执行的影响。

3.1.2 研究假设

(1)估算题目的数字消失与否影响个体的双任务协调表现, 估算题目的数字消失情况下, 个体对两个任务都回答正确的比例低, 策略选择的正确率低, 策略执行的反应时长, 错误率高。策略执行中,估算题目的数字消失与否对上调策略的影响会更大; (2)与实验1相比, 实验2中估算题目的数字消失对个体策略选择的适应性影响更明显; (3)被试会根据情境的变化调整双任务协调策略。

3.2 方法

3.2.1 被试

随机选取在校大学生40人, 男生10人, 女生30人, 平均年龄为20.55岁 。

3.2.2 实验设计

采用2(估算题目的数字消失与否：消失, 不消失)×3(策略运用条件：最佳选择, 无选上调, 无选下调)被试内实验设计, 因变量为被试问题解决的反应时和正确率。

3.2.3 实验材料

字母替代任务、两位数加法估算任务同实验1。

3.2.4 实验程序同实验1

与实验1不同的是, 要求被试先反应字母替代任务, 再反应估算任务。实验开始前告知被试两个任务同等重要, 都要既快又准的做出反应。被试同样按照先无选下调再无选上调再最佳选择的顺序完成实验, 每完成一个区组, 休息3 min。

3.2.5 数据处理

使用SPSS 16.0和Excel 2003对实验数据进行处理。

3.3 实验结果

数据分析开始前, 剔除正负3个标准差之外的数据和通过茎叶图选出的极端数据, 策略选择条件下有效被试有34人, 策略执行条件下有效被试有37人。

3.3.1 个体的双任务协调结果

个体的双任务表现描述统计结果见表4。对被试在3种实验条件下两个任务都回答正确的比率进行配对样本t检验, 分析估算题目的数字消失与否是否会对个体的双任务表现产生影响。结果显示,被试在3种实验条件下对两个任务都回答正确的比率差异显著。最佳选择条件下,t(33)=5.94,p< 0.01;无选上调条件下,t(36)=6.84,p< 0.001; 无选下调条件下,t(36)=5.62,p< 0.001。

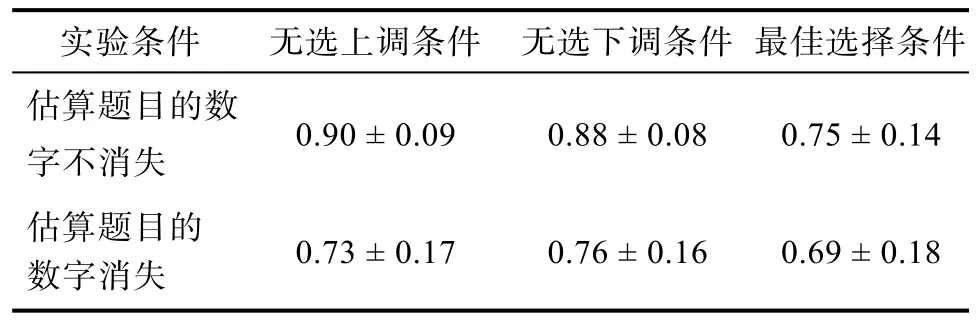
表4 在3个实验条件下被试两个任务都回答正确的比例(M ± SD)

3.3.2 不同双任务情境对个体策略运用的影响

对被试估算的反应时和正确率(表5)进行2(估算题目的数字消失与否：消失, 不消失)×2(策略执行条件：无选上调, 无选下调)重复测量方差分析。反应时上, 策略执行条件主效应显著,F(1,36)=94.17,p< 0.001, η²=0.723, 无选下调的反应时短于无选上调; 估算题目的数字消失与否的主效应边缘显著,F(1,36)=3.97,p=0.05, η²=0.099, 估算题目的数字不消失时的反应时更长。两者的交互作用显著,F(1,36)=11.03,p< 0.01, η²=0.235, 简单效应分析发现, 无选上调条件下, 估算题目的数字消失与否有明显影响,F(1,36)=11.79,p< 0.01, 估算题目的数字不消失情况下被试的反应时更长; 而在无选下调条件下, 估算题目的数字消失与否对被试的反应时没有明显影响,F(1,36)=0.21,p=0.65。

在正确率上, 策略执行条件主效应不显著,F(1,36)=0.88,p=0.35; 但估算题目的数字消失与否主效应显著,F(1,36)=52.293,p< 0.001, η²=0.529, 消失条件下的正确率低于非消失条件; 两者的交互作用显著,F(1,36)=4.34,p< 0.05, η²=0.108, 简单效应分析发现, 无选下调和无选上调条件下, 估算题目的数字消失与否均对正确率有明显影响,F(1,36)下调=26.87,p< 0.001,F(1,36)上调=40.54,p< 0.001, 但无选上调条件下, 估算题目的数字消失与否所导致的差异要大于无选下调条件。

个体在最佳选择条件下策略选择的正确率(上调题目正确选择了上调策略、下调题目正确选择了下调策略, 也就是估算结果的正确率)见表6。对正确率进行2(估算题目的数字消失与否：消失, 不消失)×2(题目类型：上调题目, 下调题目)重复测量方差分析, 结果表明, 题目类型主效应显著,F(1,33)=10.15,p< 0.05, η²=0.235, 个体在下调题目上的正确率更高; 估算题目的数字消失与否主效应显著,F(1,33)=17.34,p< 0.001, η²=0.344, 估算题目的数字消失时个体的错误率更高; 两者交互作用不显著,F(1,33)=1.22,p=0.277。

在这里, 我们进一步使用信号检测论中的判断标准C来衡量实验1、实验2中个体策略选择的适应性(Ardiale & Lemaire, 2012)。我们规定上调题目为信号, 个体使用上调策略解答上调题目为击中,使用下调策略解答上调题目为漏报, 下调题目使用下调策略为正确否定, 下调题目使用上调策略为虚报。由于两实验中被试的选取都是随机的, 可以认为两组被试间无差异。鉴于判断标准C会受到情境因素的影响, 我们推想两个实验条件、两种实验情境中个体的判断标准会存在差异。策略选择中个体判断标准和辨别力指标的描述统计结果见表7。

被试在上调题目中倾向于使用上调策略, 策略选择的适应性很高。但是对判断标准C进行2(实验条件：实验1、实验2)×2(估算题目的数字消失与否:消失、不消失)重复测量方差分析, 未发现任何主效应和交互效应。对d′进行2(实验条件：实验1、实验2)×2(估算题目的数字消失与否:消失、不消失)重复测量方差分析。结果估算题目的数字消失与否的主效应显著,F(1,57)=18.03,p< 0.001, η²=0.24,实验条件主效应不显著,F(1,57)=2.44,p=0.12。实验条件和估算题目的数字消失与否的交互作用显著,F(1,57)=6.43,p< 0.05, η²=0.101, 简单效应分析发现, 估算题目的数字不消失时, 先反应估算任务或先反应字母替代任务对策略选取的适应性影响不显著,F(1,57)=0.10,p=0.75。而估算题目的数字消失时, 先反应估算任务或先反应字母替代任务对策略选取的适应性影响显著,F(1,57)=6.03,p<0.05。估算题目的数字消失情况下, 被试需要在头脑中保持估算题信息, 这额外增加了被试的认知负荷, 使得被试的辨别力没有得到充分发挥。

表5 个体在不同策略执行条件下的估算正确率与反应时(M ± SD)

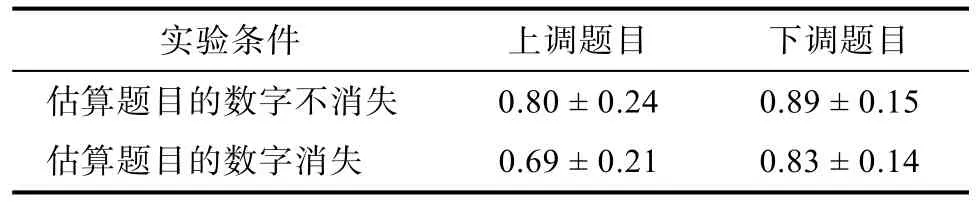
表6 个体在最佳策略选择条件下的策略选择正确率(M ±SD)

3.4 讨论

本实验发现, 估算题目的数字消失与否对个体策略执行的影响受策略执行条件的调节。在反应时上, 无论估算题目的数字消失与否, 个体在无选下调条件下的表现都没有区别, 但在无选上调条件下,当估算题目的数字不消失时, 个体的反应时要明显长于消失时。因为无选下调本身比较简单, 被试都无需将两个十位数加1, 只需看十位数即可, 所以估算题目的数字消失与否几乎不影响被试的反应时。而无选上调条件下, 被试在估算题目的数字不消失时的反应时明显变长, 这是由于实验中要求被试先对字母任务进行反应, 被试很可能出现注意偏向,将主要精力放在首先要反应的字母任务上(Sigman &Dehaene, 2006), 很可能将两个任务相继分开进行,在反应的开始集中精力于字母任务,直到对字母任务作出反应之后才开始对估算题进行反应, 使反应时延长。在正确率上, 估算题目的数字消失与否对两种条件下被试的表现均有明显影响, 且对无选上调条件下个体策略执行表现的影响大于无选下调条件, 表现为无选上调条件下被试的正确率更高。这是因为实验中要求被试先反应字母任务, 注意偏向使他们将主要精力放在字母任务上, 估算题目的数字消失条件下, 被试在对字母任务进行反应的同时要保持住估算题目信息, 这一过程可能导致估算题目的遗忘, 再加上上调策略的复杂性, 从而导致了正确率下降。而估算题目的数字不消失情况下,虽然被试将精力放在字母任务上, 但一直呈现的估算题目的数字允许被试完成字母任务后再对其进行估算, 就不存在估算题的遗忘这一问题, 所以正确率更高。我们在实验开始前要求被试又准又快的进行反应(曹雪亮等, 2004)、数据分析之前剔除正负3个标准差之外的数据和通过茎叶图选出的极端数据(仝文, 2015), 这都一定程度上对速度准确性权衡(刘彤冉, 施建农, 2007)进行了一定控制。因此,我们认为以上结果主要由于实验操纵, 而非速度−准确性权衡导致。

由于上调策略的加工过程较下调策略更繁琐,其反应时要长于下调策略(Lemaire & Lecacheur,2002)。结合本研究发现, 这似乎意味着复杂策略对双任务协调情境可能更敏感。Imbo和Vandierendonck(2007)曾发现无论是检索策略还是程序策略都受中央执行的影响。但也有研究者发现程序策略受中央执行的干扰程度相对更大(Tronsky, McManus, &Anderson, 2008), 这与本研究中的发现相类似。当估算题目的数字消失时, 个体在完成字母任务的同时需要保持住估算任务信息, 下调策略执行起来相对简单, 个体可以从头脑中直接提取答案完成, 而上调策略则需完成中间步骤, 个体必须使用某些程序策略得出问题答案, 需要消耗更多认知资源。

研究结果还显示, 在估算题目的数字消失时,实验2中被试的d′值偏低。个体在双任务情境中可能需要付出额外努力(Kittler, Krinsky-McHale, &Devenny, 2008)。Imbo和LeFevre (2011)也曾指出中国被试很可能更容易受外界环境的影响, 在压力情况下, 他们的策略适应性很低。本实验中两个刺激的呈现时间都较短, 估算题目的数字消失时, 根据Miller, Ulrich和Rolke (2009)提出的最佳化原则,为保证对两个任务的反应时间最短, 个体在实验2中加工完字母替代任务之后, 不会再花费更多时间对估算任务进行分析, 从而更多地选择了操作相对简单的下调策略。

4 总讨论

本研究采用估算任务和字母替代任务, 尝试通过变换刺激呈现方式、反应顺序, 深入考察了双任务情境下个体进行策略选择与策略执行的表现差异, 试图揭示中央执行成分中的双任务协调能力在算术策略运用中扮演的重要角色。

表7 最佳选择条件下个体判断标准和辨别力指标的描述统计结果(M ± SD)

4.1 双任务协调影响个体算术策略执行

本研究发现双任务协调会对个体的策略执行产生影响。实验2中个体在估算题目的数字消失时,策略执行的错误率更高。但实验1中, 个体在两种无选条件下都未表现出正确率上的差异, 说明双任务协调对任务的影响, 同任务的反应顺序、情境复杂程度有一定关系。陈英和和王明怡(2009)曾发现个体在有中央执行负荷条件下, 策略执行表现更差,这与本研究结果相似。

此外, 执行上调策略时受到的影响大于下调策略, 这可能与策略本身的操作复杂程度有关。个体执行上调策略时需要将每个加数的十位数字向上进1, 然后再相加, 导致反应时间长、错误率高, 而下调策略相对比较简单, 可以直接从记忆中提取答案(Lemaire & Lecacheur, 2002)。在双任务情境中,下调策略需要的认知资源较少, 个体解决问题时,可以达到自动化程度, 从而可将大部分资源集中于字母替代任务上。Tronsky等(2008)的研究也证实了个体在双任务情境中, 程序性计数策略受到的干扰相对更多一些。

4.2 双任务协调影响个体算术策略选择

同策略执行相比, 双任务协调似乎对策略选择的制约作用更为明显。个体在策略选择中需要付出更多的认知努力, 还存在一个策略判断过程。本研究两项实验结果表明, 无论双任务情境简单或复杂,个体都倾向于选择相对简单的下调策略, 但是当后反应估算任务时, 这种影响会表现得更大一些。这就支持了前人所发现的“双任务协调受任务反应顺序的影响” (Leonhard et al., 2011)。也与Imbo和LeFevre(2009, 2011)的发现一致。有研究证实个体可以实现项目内的策略转换(Ardiale & Lemaire, 2012), 个体选择一个策略去执行特定问题, 会同时评估该策略的有效性, 若发现该策略不是最佳策略, 认知系统会修正最初的选择而转向最佳策略, 这些认知加工过程都需要消耗个体有限的认知资源。本研究中,当估算题目的数字不消失, 或者要求个体先反应估算任务时, 个体的认知资源相对充足, 可进行策略的在线转换, 确保策略选择的正确性, 但在估算题目的数字消失时, 双任务情境本身已消耗了个体大量的注意资源, 加上项目内策略转换产生的转换代价, 从而导致个体偏向于选择较简单的下调策略。

4.3 研究意义与不足

以往许多对算术认知策略的研究主要围绕工作记忆以及其中的中央执行这一成分进行(王明怡,陈英和, 2006; 司继伟等, 2012), 正如引言中提到的中央执行对个体的算术任务表现有着重要影响,那么本研究对中央执行中的双任务协调功能对个体算术策略运用影响的研究将有助于深入理解中央执行功能在个体算术策略运用上的作用机制, 细化对算术认知策略的研究。

本研究结果与前人发现相一致, 即双任务协调能力会对个体的任务表现产生影响(Szameitat et al., 2006;Schubert et al., 2008)。此外, 结合已有文献(陈英和,王明怡, 2009)和本研究结果, 可以认为双任务协调能力在作用于相关任务操作的同时, 也需要其他中央执行成分的共同参与, 比如抑制和转换。双任务协调能力虽然可以调整两个任务的加工顺序(Leonhard &Ulrich, 2011), 决定两个任务的重叠程度(Schubert et al.,2008), 但在两个不同任务操作的相互作用过程中,也需要在不同任务之间实现灵活转换和信息的在线更新, 同时抑制无关信息的干扰。其次, 本研究中使用的选择/无选法范式属于研究估算策略灵活性的常用范式(Xu, Wells, LeFevre, & Imbo, 2014)。对不同双任务情境(两种呈现方式、两种呈现顺序)下策略运用表现变化的考察, 进一步揭示了个体究竟如何根据任务情境的变化灵活地选择并执行算术策略。被试在当前任务中会根据不同双任务情境及任务难度来调整认知资源的分配, 这也从侧面说明当前被试的表现更符合双任务协调的执行控制交互作用模型。可以说, 本研究间接为执行控制交互作用模型这一双任务协调理论的存在及有效性提供了一定底层证据支持。

5 结论

基于上述结果与分析, 本实验条件下可得到如下结论：

(1)双任务情境呈现方式影响个体的算术策略运用表现。表现为在估算题目的数字消失条件下,个体策略选择和策略执行的正确率相对较低。

(2)个体对双任务的反应顺序会影响算术策略运用。当先反应字母替代任务时, 个体的估算策略受双任务协调的影响会更明显。

(3)个体会根据情境变化调整双任务协调的策略, 其表现更加符合执行控制交互作用理论。

Ardiale, E., & Lemaire, P. (2012). Within-item strategy switching: An age comparative study in adults.Psychologyand Aging, 27(4), 1138–1151.

Baddeley, A. D., & Hitch, G. (1974). Working memory.The Psychology of Learning and Motivation,8(2), 47–89.

Campbell, J. I. D. (2005).Handbook of mathematical cognition. New York: Psychology Press.

Cao, X. L., Miao, D. M., Huang, F. E., Hou, Y. H., Sun, Y. F.,Shi, Y. F., & Li,Y. (2004). An experimental research of mental fatigue using a working memory test.Chinese Journal of Clinical Psychology, 12(4), 331–334.

[曹雪亮, 苗丹民, 皇甫恩, 侯艳红, 孙云峰, 史衍峰, 李媛.(2004). 工作记忆测量脑力疲劳的实验研究.中国临床心理学杂志, 12(4), 331–334.]

Chen, Y. H., & Wang, M. Y. (2009). The relationship between executive functions and arithmetical cognitive strategies of children.Psychological Science, 32(1), 34–37.

[陈英和, 王明怡. (2009). 儿童执行功能与算术认知策略的关系.心理科学,32(1), 34–37.]

Hodzik, S., & Lemaire, P. (2011). Inhibition and shifting capacities mediate adults’ age-related differences in strategy selection and repertoire.Acta Psychologica, 137(3), 335–344.

Imbo, I., & LeFevre, J. (2009). Cultural differences in complex addition: Efficient Chinese versus adaptive Belgians and Canadians.Journal of Experimental Psychology: Learning,Memory, and Cognition, 35(6), 1465–1476.

Imbo, I., & LeFevre, J. (2011). Cultural differences in strategic behavior: A study in computational estimation.Journal of Experimental Psychology, Learning, Memory, and Cognition,37(5), 1294–1301.

Imbo, I., & Vandierendonck, A. (2007). The role of phonological and executive working memory resources in simple arithmetic strategies.European Journal of Cognitive Psychology,19(6), 910–933.

Kittler, P. M., Krinsky-McHale, S. J., & Devenny, D. A.(2008). Dual-task processing as a measure of executive function: A comparison between adults with Williams and Down syndromes.American Journal on Mental Retardation,113(2), 117–132.

Lemaire, P., & Lecacheur, M. (2002). Children's strategies in computational estimation.Journal of Experimental Child Psychology, 82(4), 281–304.

Lemaire, P., & Lecacheur, M. (2010). Strategy switch costs in arithmetic problem solving.Memory and Cognition, 38(3),322–332.

Lemaire, P., & Lecacheur, M. (2011). Age-related changes in children’s executive functions and strategy selection: A study in computational estimation.Cognitive Development,26(3), 282–294.

Leonhard, T., Fernández, S. R., Ulrich, R., & Miller, J. (2011).Dual-task processing when task 1 is hard and task 2 is easy:Reversed central processing order?Journal of Experimental Psychology: Human Perception and Performance, 37(1),115–136.

Leonhard, T., & Ulrich, R. (2011). Determinants of central processing order in psychological refractory period paradigms:Central arrival times, detection times, or preparation?The Quarterly Journal of Experimental Psychology, 64(10),2012–2043.

Liu, T. R., & Shi, J. N. (2007). Speed-accuracy trade-off effect on children’s visual search.Chinese Journal of Clinical Psychology, 15(4), 359–362.

[刘彤冉, 施建农. (2007). 儿童视觉搜索的速度-正确率平衡.中国临床心理学杂志, 15(4), 359–362.]

Miller, J., Ulrich, R., & Rolke, B. (2009). On the optimality of serial and parallel processing in the psychological refractory period paradigm: Effects of the distribution of stimulus onset asynchronies.Cognitive Psychology, 58(3),273–310.

Peng, H. M., Zhang, L., & Shen, J. L. (2009). Aging of the central executive function of working memory.Psychological Science, 32(1), 67–70.

[彭华茂, 张凌, 申继亮. (2009). 工作记忆中央执行功能的老化研究.心理科学, 32(1), 67–70.]

Schneider, D. W., & Anderson, J. R. (2010). Asymmetric switch costs as sequential difficulty effects.The Quarterly Journal of Experimental Psychology, 63(10), 1873–1894.

Schubert, T., Fischer, R., & Stelzel, C. (2008). Response activation in overlapping tasks and the response-selection bottleneck.Journal of Experimental Psychology: Human Perception and Performance, 34(2), 376–397.

Si, J. W., Xu, Y. L., Feng, H. M., Xu, X. H., & Zhou, C. (2014).Differences of arithmetic strategy use in adults with different math anxieties: An ERP study.Acta Psychologica Sinica, 46(12), 1835–1849.

[司继伟, 徐艳丽, 封洪敏, 许晓华, 周超. (2014). 不同数学焦虑成人的算术策略运用差异: ERP研究.心理学报,46(12), 1835–1849.]

Si, J. W., Yang, J., Jia, G. J., & Zhou, C. (2012). The effect of central executive load on adult’s strategy using in computational estimation.Acta Psychologica Sinica, 44(11),1490–1500.

[司继伟, 杨佳, 贾国敬, 周超. (2012). 中央执行负荷对成人估算策略运用的影响.心理学报, 44(11), 1490–1500.]

Siegler, R. S., & Lemaire, P. (1997). Older and younger adults'strategy choices in multiplication: Testing predictions of ASCM using the choice/no-choice method.Journal of Experimental Psychology General, 126(1), 71–92.

Sigman, M., & Dehaene, S. (2006). Dynamics of the central bottleneck: Dual-task and task uncertainty.PLoS Biology,4(7), e220.

Szameitat, A. J., Lepsien, J., von Cramon, D. Y., Sterr, A., &Schubert, T. (2006). Task-order coordination in dual-task performance and the lateral prefrontal cortex: An eventrelated fMRI study.Psychological Research, 70(6), 541–552.

Tong, W. (2015).The research of orthographic satiation and semantic satiation in Chinese(Unpublished doctorial dissertation).Tianjin Normal University, Tianjin.

[仝文. (2015).汉字字形与语义饱和现象研究(博士学位论文). 天津师范大学, 天津.]

Tronsky, L. N., McManus, M., & Anderson, E. C. (2008).Strategy use in mental subtraction determines central executive load.The American Journal of Psychology, 121(2),189–207.

Uittenhove, K., & Lemaire, P. (2012). Sequential difficulty effects during strategy execution: A study in arithmetic.Experimental Psychology, 59(5), 295–301.

Wang, M. Y., & Chen, Y. H. (2006). The influence of central executive of working memory on children's arithmetical cognitive strategies.Psychological Development and Education, 22(4), 24–28.

[王明怡, 陈英和. (2006). 工作记忆中央执行对儿童算术认知策略的影响.心理发展与教育, 22(4), 24–28.]

Xu, C., Wells, E., LeFevre, J. A., & Imbo, I. (2014). Strategic flexibility in computational estimation for Chinese-and Canadian-educated adults.Journal of Experimental Psychology:Learning, Memory, and Cognition, 40(5), 1481–1497.

Yang, J. (2012).Central executive load on age-related differences in strategy use: The case of computational estimation(Unpublished master’s thesis). Shandong Normal University,Ji’nan.

[杨佳. (2012).中央执行负荷影响算术策略运用的年龄相关差异: 以估算为例(硕士学位论文). 山东师范大学, 济南.]

Zhang, H. D., Wang, Y. X., Hu, D. M., Li, H. X., & Si, J. W. (2015).Central executive components and individuals’ arithmetic strategy use with field-dependence/field- independence cognitive style: An eye movement study.Psychological Research, 8(1), 43–51.

[张红段, 王玉璇, 胡冬梅, 李红霞, 司继伟. (2015). 场认知风格、中央执行成分影响个体算术策略运用的眼动研究.心理研究, 8(1), 43–51.]