使用验证性补偿多维IRT模型进行认知诊断评估*

詹沛达 陈 平 边玉芳

(北京师范大学中国基础教育质量监测协同创新中心, 北京 100875)

1 引言

人们已不满足于只能分析出一个总分的教育与心理测量方法, 具有诊断功能的测量方法因此逐渐受到人们的关注。基于此, 测验编制者希望借助被试的作答结果获得更加丰富的信息, 以便对被试做出更客观更有针对性的评估和补救。认知诊断评估作为一种将形成性评估和终结性评估相结合的综合评估形式, 其最终目的是为了更有效地促进学生的发展, 其作为一种评估手段, 更关注的应是评估后如何更有效地对学生进行补救教学, 或是如何修正现有教学的过程与方法以促进学生更有效地成长。近些年, 认知诊断模型(cognitive diagnostic models, CDMs)得到快速发展, 常见的有DINA(Junker & Sijtsma, 2001)、LCDM (Henson, Templin,& Willse, 2009)和G-DINA (de la Torre, 2011)等; 另一些拓广模型(比如, Embretson & Yang, 2013;Huang & Wang, 2014; Li & Wang, 2015; Templin &Bradshaw, 2014; 詹沛达, 李晓敏, 王文中, 边玉芳,王立君, 2015)也被提出并建议使用在特定的测验情境中。

在CDMs闪耀着光芒的同时, 多维IRT模型(multidimensional IRT models, MIRTMs)似乎受到些许冷落。而实际上, MIRTMs和CDMs一样也具有诊断功能(Embretson & Yang, 2013; Stout, 2007;Wang & Nydick, 2015), 只不过因为MIRTMs是在连续量尺上刻画或诊断被试的潜变量值, 并没有直接或明确地对被试进行分类, 导致我们放大了其根据子维度分排序的功能。另外, 随着家长及学生对反馈信息精细化的要求越来越高, 当前CDMs中对属性精细化的研究越来越多(比如, Karelitz, 2004;von Davier, 2005; 詹沛达, 边玉芳, 王立君, 2016),也有研究直接采用属性掌握概率这一连续变量(Zhan, Wang, Li, & Bian, 2016; 詹沛达, 边玉芳,2015)来进行认知诊断。即不仅希望要诊断出掌握状态, 还要了解到掌握程度, 而对潜变量的精细化描述恰恰是MIRTMs的优势。

MIRTMs与CDMs的主要区别在于前者假设潜变量空间由K维连续变量(即潜在特质)组成, 而后者假设潜变量空间由K维离散变量(即属性)组成。而至于如何在这两类模型中进行选择, 则通常取决于测验目标潜变量的含义和测验目的, 若目标潜变量的含义相对较大或粒度较大(比如数学能力)则MIRTMs更为常用, 而若含义相对较小或粒度较小(比如分数进位)则CDMs更为常用; 若测验目的是探究被试在某方面能力的大小则MIRTMs更为常用, 而若测验目的仅为诊断被试是否掌握某方面的能力则CDMs更为常用。当然, 万事非绝对, 暂无研究和证据表明我们一定要按某种规则选用两者中的某一个。

通常根据潜变量之间的关系, 无论是MIRTMs还是CDMs均大体可分为补偿模型和非补偿模型这两类。补偿模型认为被试在某一维度的优势可以去弥补其在其他维度的劣势, 进而假设潜变量之间为累加求和关系; 而非补偿模型认为只有被试拥有或达到该题目所考查的所有维度的要求才有较高的概率正确作答该题目, 进而假设潜变量之间为连乘关系。另外, 自MIRTMs和CDMs诞生起, 关于两者的研究长期是相互分离和独立的, 直到近些年才有研究去触碰这两类模型的交叉点(比如,Bradshaw & Templin, 2014; Embretson & Yang,2013; Wang & Nydick, 2015; 詹沛达等, 2015)。这也在一定程度导致“补偿”和“非补偿”这两个概念在MIRTMs和CDMs中的建模(量化)描述是有所差异的。鉴于本文主题且为便于区分, 下文将MIRTMs中的“非补偿”称为部分补偿(partially-compensatory)(Reckase, 2009), “补偿”仍保留原有含义(即潜在特质之间的累加); 而把CDMs中的“非补偿”称为连接(conjunctive) (Maris, 1999), 把“补偿”限定于补偿连接缩合规则(Maris, 1999) (即属性之间的累加),而不包含以DINO模型为例的分离(disjunctive)缩合规则(Maris, 1999)。基于上述概念区分, 可知在“补偿”的含义下MIRTMs和CDMs对潜变量之间的关系具有相同的量化定义, 这也为本文后续研究中对比探究这两类模型的认知诊断功能奠定了基础。另外, Bolt和Lall (2003)也指出当使用补偿MIRTMs去拟合由部分补偿MIRTMs产生的数据时,补偿MIRTMs的拟合结果与部分补偿MIRTMs的拟合结果一样好; 反过来, 由部分补偿MIRTMs去拟合由补偿MIRTMs产生的数据时却无法得到与使用补偿MIRTMs自身去拟合该数据一样好的结果。因此, 补偿MIRTMs在实际应用中比部分补偿MIRTMs更为普遍。

结合本文主题, 下面首先介绍验证性补偿多维两参数Logistic模型(confirmatory compensatory multidimensional two-parameter Logistic model,CC-M2PLM)及其诊断功能的具体化, 然后通过模拟研究对比探究CC-M2PLM和线性Logistic模型(linear Logistic model, LLM) (Maris, 1999)的认知诊断功能。模拟研究结果表明CC-M2PLM可用于诊断测验数据分析, 且认知诊断功能与直接使用LLM的效果相当; 最后, 以两则实证数据为例来说明CC-MIRTMs在实际诊断测验分析中的可行性。

2 CC-M2PLM及其认知诊断功能

2.1 CC-M2PLM介绍

在众多CDMs中, 假设属性间满足补偿关系的LLM近些年逐渐受到研究者的提及和关注(比如,de la Torre, 2011; 詹沛达等, 2015), 主要原因是：在特定题目中LLM可以把被试的属性掌握模式细分为组(其中表示题目i所考查的属性总数), 这比常用的DINA模型中的2组(即全掌握组和未全掌握组)要精细许多。与LLM相对应, 补偿M2PLM (compensatory M2PLM, C-M2PLM)是补偿MIRTMs中一个较为常用的模型。限于篇幅原因,LLM的题目反应函数(item response function, IRF)及其中参数含义详见Maris (1999)和詹沛达等(2015); 而C-M2PLM的IRF及其中参数含义详见Reckase (2009)。

C-M2PLM在建构之初实为一种探索性(exploratory)模型(Embretson & Yang, 2013), 即假设K维潜在特质均对题目i的正确作答概率产生影响。这相当于探索性因素分析中假设所有潜在变量均在观察变量(作答)上有载荷(区分度)。然后根据每个维度上的区分度参数估计值来判断该维度是否对该题目的正确作答概率产生影响, 若无影响则该维度上的区分度参数接近于0。在CDMs中Q矩阵为一种验证性矩阵(confirmatory matrix), 用于指定题目和维度之间的关系, 可以简化模型及参数估计的复杂性。借鉴该优点, 可通过在探索性C-M2PLM(exploratory C-M2PLM)中引入Q矩阵来限定题目与各维度潜在特质之间的关系, 进而得到验证性的C-M2PLM (记为CC-M2PLM), 则CC-M2PLM的IRF可被描述为：

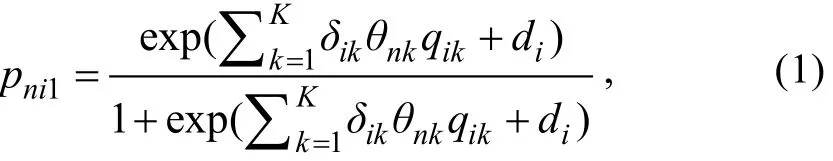
式中pni1表示被试n在题目i上的正确作答概率,δi=(δi1,δi2,...,δiK)’是K×1维的题目区分度参数向量,θn=(θn1,θn2,...,θnK)’是K×1维的潜在特质参数向量(通常θnk∈(-3, 3)),di是截距参数。类似对模型引入验证性矩阵的做法亦可参见Embretson和Yang(2013)、Wang和Nydick (2015)。对比LLM和CC-M2PLM可发现, 仅从IRF上来看两者完全一样且均属于验证性模型范畴。当然, 由于两者分别属于MIRTMs和CDMs, 所以两者的主要差异体现在对潜在变量的量化描述方式上：CC-M2PLM中一般假设K维潜在特质满足多元正态分布, 即; 而LLM中假设潜在特质向量满足狄利克雷(Dirichlet)分布, 即假设1×K维属性模式从2K种属性模式中按某种概率抽取。这导致两种模型中的被试参数量尺是不同的, 因此为了实现CC-M2PLM的认知诊断功能就需要对CC-M2PLM中的被试参数进行某种转换(详见2.2节)。

本研究旨在探究模型的认知诊断功能, 所以相对于题目参数返真性而言, 我们更关注被试参数的估计返真性。另外, 鉴于这两类模型中题目参数的含义不同, 缺乏直接比较的意义。所以下文不再呈现题目参数的估计结果。而这两类模型中的题目参数之间是否存在关系、存在哪种关系, 值得今后进行进一步的探究。

2.2 对CC-MIRTMs认知诊断功能的具体化

CDMs与MIRTMs的主要差异在于对同一潜变量使用了不同的量尺进行刻画。在CC-MIRTMs中假设潜变量为连续变量, 而CDMs中假设潜变量为离散变量, 所以为使两者具有可比性同时使CC-MIRTMs具有认知诊断功能, 就需要对CC-MIRTMs的潜变量进行转换。对此, 可以尝试使用切点(cutoff point,CP)法：当连续的潜在特质值大于等于CP时, 可判断被试掌握该潜在特质; 否则判断被试未掌握该特质。在DCM中, CP法通常被用于生成具有相关性的属性(Chiu, Douglas, & Li, 2009; Wang, Chang, &Huebner, 2011; 詹沛达等, 2016), 如下：

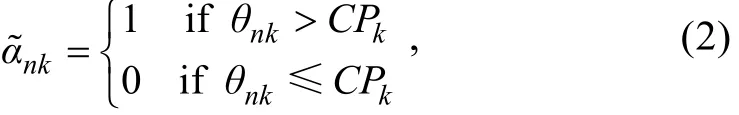
式中,θnk为被试n的第k维潜在特质值,CPk表示第k维潜在特质上的切点,表示由被试n的第k维潜在特质值转换得到的掌握状态。而且为了与CDMs中的属性(αnk)进行区分, 下文称为跨界属性(transborder attributes)。具体的切点选择方法详见3.3节。

由于式(2)仅是对被试潜在特质的一个转换,并不涉及参数估计过程, 所以该方法可能具有如下优势：(1)可以同时报告具体潜在特质值和掌握状态,可满足不同的测验目的; (2)被试潜在特质参数与题目参数的量尺并未发生变化, 已有的MIRTMs题库可继续使用; (3)相比于CDMs, 对MIRTMs进行参数估计的软件相对更为成熟和丰富, 可直接使用;(4)所有MIRTMs中的统计指标均可直接使用; (5)模拟研究中可借助CDMs中的部分相关统计指标来对参数估计返真性进行探究, 比如采用属性判准率来评估被试参数的返真性。

3 模拟研究：CC-M2PLM的诊断能力探究及其与LLM的对比

3.1 研究目的与设计

模拟研究将以具有认知诊断功能的LLM为“真实”模型来生成作答数据, 并视其为诊断测验数据,并同时采用CC-M2PLM和LLM来拟合数据。诊断分析结果以LLM的诊断结果为基线, 进而探究CC-M2PLM与LLM的诊断结果之间的近似程度。如果两者的诊断结果非常接近甚至几乎一致, 则可说明CC-M2PLM具有较好的认知诊断功能; 反之,若两者的诊断结果差异非常大, 则说明CC-M2PLM的认知诊断功能有限。因为本研究需采用式(2)对CC-M2PLM的潜在特质估计值进行划分, 而不同的切点设定可能会导致潜在特质被转换为不同的跨界属性, 本文先通过一个预研究以寻找合适的切点。

3.1.1 自变量参数设定

选取主要影响被试参数估计的三个因素作为自变量：(1)属性数量K：少(3)、中(5)、多(7); (2)属性间四分相关(tetrachoric correlation)系数ρ：低(0.3)、中(0.65)、高(0.9); (3)题目数量I：少(15)、中(30)、多(60)。

3.1.2 被试参数与题目参数设定

设定被试数量为N=3000, 按如下方法生成被试属性：(1)依据多元正态分布MVNK(0, Σ)生成K维连续变量矩阵; (2)设定各连续变量满足标准正态分布, 之后以0为切点对各连续变量进行两段切割;(3)通过设定Σ矩阵来调控各多分属性之间的四分相关。另一方面, 设定所有题目的猜测概率均为0.1,非失误均为0.9。由于LLM采用logit连接函数, 所以需要把所有题目的截距参数均设定为-2.197, 题目i对属性k的权重参数设定为。

3.1.3 测验Q矩阵的建构

在诊断测验中, 可达矩阵R是实现对每个属性准确诊断的前提条件(丁树良, 杨淑群, 汪文义,2010)。因为本研究不考虑属性层级结构假设(Leighton, Gierl, & Hunka, 2004), 所以R矩阵为单位阵。本研究设定：(1)每个测验Q矩阵中有且仅包含2个R矩阵(依据属性数量分别有6、10、14题); (2)测验Q矩阵中除2个R矩阵以外的行随机从(2K−1)种不含全0模式的属性模式中随机抽取;(3)尽量保证每个属性在所有题目上的平均考查次数相等。

3.2 模拟作答、参数估计及评估指标

采用R软件(version 3.2.2 64-bit; R Core Team,2015)自编程序进行模拟作答生成。根据各参数“真值”和LLM计算被试n在题目i上的正确作答概率pni1,则被试作答服从伯努利分布,。本研究使用R软件中的mirt包(Version 1.14;Chalmers et al., 2015)和CDM包(Version 4.6-0;Robitzsch, Kiefer, George, & Uenlue, 2015)分别对CC-M2PLM和LLM进行参数估计。对于LLM, 选用默认的EM算法; 而对于CC-M2PLM, 由于涉及高维计算(MIRTMs在参数估计过程中涉及对协方差矩阵进行估计, 所以目前5维或7维对于一般的EM算法来说非常具有挑战性), 这里我们选用相对更适合的MH-RM算法(Cai, 2010)。附录部分呈现了对这两个程序包的具体设定, 供实际测验分析者参考。本研究对整个模拟过程重复30次, 以减少随机误差影响。

本研究采用属性判准率(ACCR)和属性模式判准率(PCCR)作为被试参数估计返真性的评价指标(Chen, Xin, Wang, & Chang, 2012)。注意在使用ACCR和PCCR探究CC-M2PLM的被试参数返真性前, 需先采用式(2)将潜在特质估计值转换为跨界属性估计值, 具体的切点设置方法详见3.3节。

3.3 预研究：切点的选定

Templin和Bradshaw (2013)指出使用CDMs分析由IRMs生成的作答数据时, CDMs会按照IRT量尺上的0点把潜在特质θ划分为掌握和未掌握两类。对此, 本文简单重复Templin和Bradshaw (2013)的研究, 并作为预研究以探究适合本研究的切点：即使用CC-M2PLM生成作答数据并使用LLM去分析该数据。由于是预研究, 本文将简化其实验条件(K=3、N=3000、I=30、ρ =0.2), 则, 其中

预研究结果如图1所示, 这与Templin和Bradshaw (2013)的结论基本一致, 即被试的潜在特质“真值”大体上是以0点为分界线被估计为和两类。

由于数据本身没有发生变化, 则隐藏在该数据背后的潜在建构(即潜变量)也没有发生变化, 所以即便我们使用不同的数据分析方法或模型去量化该潜变量(即刻画在不同的量尺上), 这些量化数值之间也必定存在某种数学转换关系。我们可尝试从量尺角度来看切点选择的问题, 可以对logistic量尺上的值(θ)进行转换, 将其转换到0～1量尺上：, 此时δ所在的0～1量尺其实就是属性掌握概率量尺(Zhan, Wang, Bian et al., 2016; 詹沛达, 边玉芳, 2015)。通常, 在该量尺下可以以0.5为切点将属性掌握概率转换为0和1的属性掌握状态(de la Torre & Douglas, 2004)。可发现当δ=0.5时,有θ=0, 这与上述预研究中得到被试潜在特质“真值”大体上以logistic量尺上的0点为分界线的结果相符。那么, 基于上述结果且为简化研究又不失一般性, 下文正式模拟研究将在IRT的logistic量尺上设定所有维度的切点相等：CPk=0, 即当潜在特质为正值时, 跨界属性为1 (掌握)。

图1 使用LLM去估计由CC-M2PLM生成的作答数据的结果

3.4 模拟研究结果

表1中列出了分别使用LLM和CC-M2PLM去拟合由LLM生成的诊断测验数据的结果(限于篇幅仅列出K=7的结果, 其余条件详见图2)。首先, 可以看到无论是在哪种实验条件下, CC-M2PLM的ACCR和PCCR指标值与作为“真实”模型的LLM的指标值是基本一致的, 且绝大多数差异都在千分位上。其次, 各自变量条件对CC-M2PLM和LLM的诊断结果影响也是一致的。根据表1和图2中结果, 足以说明通过式(2)对CC-M2PLM中被试潜在特质估计值进行转换, 确实能够使CC-M2PLM展现出其本有的认知诊断功能, 且其认知诊断表现与LLM的认知诊断表现几乎一致。另外, 我们并没有直接探究CC-M2PLM的参数估计返真性问题, 原因是：(1)本文旨在探讨CC-M2PLM的认知诊断功能, 因此直接分析一个诊断测验数据更符合主题;(2)用LLM去拟合LLM本身生成的数据其参数估计返真性不是问题, 那么用CC-M2PLM去拟合同一批数据能够得到与LLM相一致的结果也足以说明CC-M2PLM的参数返真性较好。

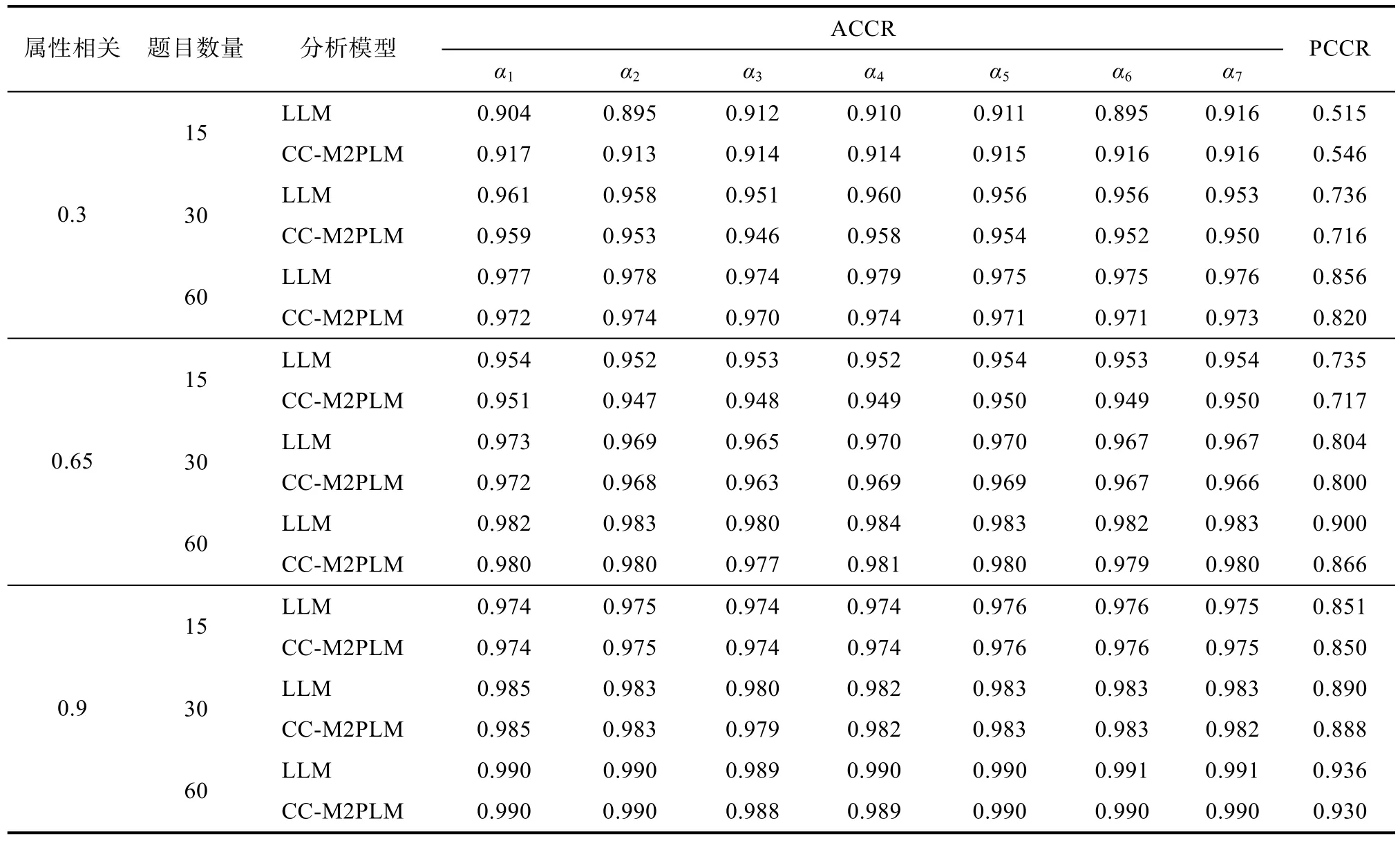
表1 LLM与CC-M2PLM的被试参数估计返真性(K=7)

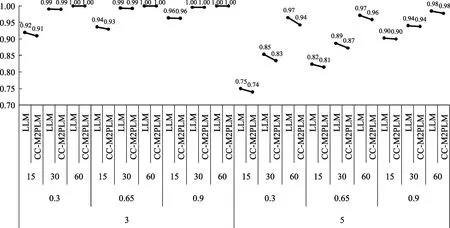
图2 LLM与CC-M2PLM的被试参数估计返真性(PCCR, K=3 & 5)

如上文所述, CC-M2PLM除了能给出“掌握”或“未掌握”的诊断结果外, 还能够给出被试潜在特质的具体估计值。表2呈现了(在K=3、ρ=0.3、I=30的条件下)4名被试的潜在特质维度估计值和相对应的属性模式估计结果, 以被试3和4为例, 尽管两者的跨界属性(模式)一致, 但相对更为精准的潜在特质估计值还是存在些许差异。此外, 我们还在[−0.5, 0.5]范围内为CPk选取11个节点, 并分别计算转换后的跨界属性的返真性, 结果表明CPk=0时的ACCR和PCCR均为最高, 而其他CPk设定均会降低CC-M2PLM的判准率。

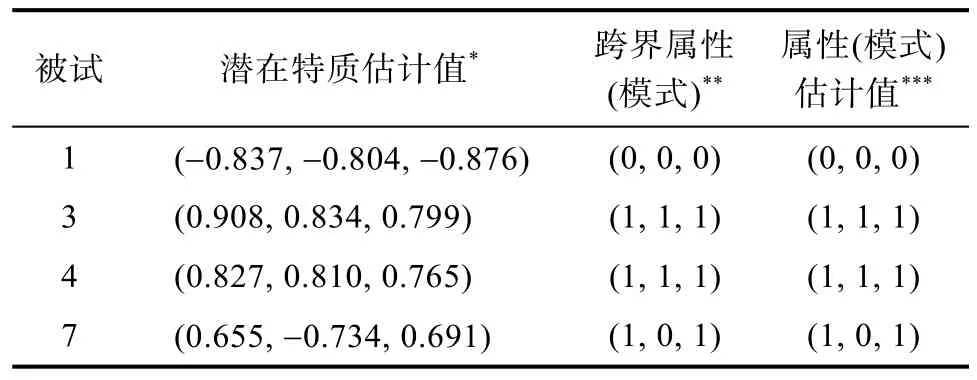
表2 CC-M2PLM与LLM的被试参数估计值对比

综上所述, 模拟研究结果表明使用式(2)将潜在特质转换为跨界属性后, 再使用CC-M2PLM分析诊断测验数据的方法具有可行性。这为下文实证数据分析提供了前提保证。

4 实证数据分析

实证数据分析包含两个子研究, 分属于数学和英语测验数据。模型-数据拟合指标涉及：标准化残差均方根(SRMR)、近似误差均方根(RMSEA)、Tucker-Lewis指数(TLI)、比较拟合指数(CFI)、-2×log(likelihood) (即2LL)、AIC以及BIC。

4.1 实证数据分析1：分数减法数据

选用de la Torre (2009)一文中对分数减法(fraction subtraction)数据(Tatsuoka, 2002)的描述, Q矩阵见图3。该数据中I=15、K=5、N=536。同样使用LLM、CC-M2PLM与DINA去拟合该数据。

表3给出了模型−数据拟合指标值。3个模型的SRMR指标值分别为0.090、0.094和0.103, 表明模型-数据拟合勉强可被接受。综合4个拟合指标(SRMR < 0.1、RMSEA < 0.05、TLI > 0.9、CFI > 0.9)可知CC-M2PLM对分数减法数据具有较好的拟合结果。CC-M2PLM的−2LL、AIC和BIC在3个模型中均最小, 说明CC-M2PLM对该数据的拟合结果相对最好。LLM对该数据的拟合结果优于DINA。

表4呈现了随机选取的5名被试的潜在特质维度估计值和相对应的跨界属性(模式), 以被试135和415为例, 尽管两者的跨界属性(模式)一致, 但相对更为精准的潜在特质估计值仍存在差异。被试2和57的潜在特质估计值完全一致, 这因为两者的作答模式完全一致。从这两组被试的结果可以看出,当作答模式存在些许差异时(被试135错误作答所有题目, 而被试415仅正确作答了第5题), 跨界属性(模式)或由LLM估计得到的属性(模式)估计值都无法精准地区分他们, 而基于CC-M2PLM估计得到的潜在特质估计值却能够在跨界属性(模式)的基础上更精准地区分他们：第5题仅考查属性3, 被试135和415的潜在特质估计值也可发现差值最大的为属性3; 而当作答模式完全一致时, 即便更为精准的潜在特质估计值也可以得到相同的估计值。

4.2 实证数据分析2：ECPE数据

本研究实证数据来自ECPE (Examination for the Certificate of Proficiency in English)。该数据中I=28、K=3、N=2922。Q矩阵见图4, 其中α1到α3分别代表：句法规则(morphosyntactic rules)、衔接规则(cohesive rules)和词汇规则(lexical rules)。分别使用属于补偿模型的LLM和CC-M2PLM与属于连接模型的DINA去拟合该数据。

图3 分数减法数据的Q矩阵(K × I 的Q’矩阵。其中, “灰色”为1, “空白”为0)

表3 分数减法数据的模型−数据拟合结果

表4 分数减法数据的诊断报告样例

图4 ECPE数据的Q矩阵(K × I 的Q’矩阵。其中, “灰色”为1, “空白”为0)

表5 ECPE数据的模型-数据拟合结果

表5给出了模型-数据拟合指标值。3个模型的SRMR指标值分别为0.020、0.032和0.033, 表明模型-数据拟合理想。对CC-M2PLM而言, RMSEA <0.05、TLI > 0.95、CFI > 0.95, 结合SRMR指标后表明CC-M2PLM的模型-资料拟合情况理想。CC-M2PLM的−2LL、AIC和BIC在3个模型中均最小, 说明CC-M2PLM对该数据的拟合结果相对最好。LLM对该数据的拟合结果优于DINA, 表明该数据中的3个属性之间更倾向是补偿关系而非连接关系。

5 总结与展望

本文首先介绍两个分别隶属于MIRTMs和CDMs的验证性补偿模型：CC-M2PLM和LLM。其次, 为两者具有可比性, 本文尝试性地把CC-M2PLM中的潜在特质转换为属于分类变量的跨界属性, 以期具体化其认知诊断功能。然后, 通过模拟研究探究CC-M2PLM的认知诊断功能, 结果表明CC-M2PLM可用于诊断测验数据分析, 其认知诊断功能与LLM一样好。最后, 以两则实证诊断测验数据为例来探究CC-M2PLM的实际应用性。当然任何事物都是相对而言的, 使用MIRTMs也需要付出诸如相对更长的参数估计耗时、题目参数与CDMs中的题目参数含义存在差异等代价。

由于篇幅有限且为聚焦研究主题, 本文对部分研究条件做了简化或限定：(1)Q矩阵界定正确; (2)被试数量固定; (3)仅考虑MIRTMs中的两参数模型等, 而这些限定的研究条件也均可能是判准率的影响因素, 开放这些条件后MIRTMs的表现如何值得进一步探究。另外, 本研究未关注题目参数, 主要原因在于MIRTMs中的题目参数与CDMs中的题目参数之间的关系还有待进一步探究。再有, 本研究仅关注补偿模型, 而非补偿(i.e., 部分补偿和连接)模型的认知诊断功能也值得探究。

Bolt, D. M., & Lall, V. F. (2003). Estimation of compensatory and noncompensatory multidimensional item response models using Markov chain Monte Carlo.Applied Psychological Measurement, 27, 395–414.

Bradshaw, L., & Templin, J. (2014). Combining item response theory and diagnostic classification models: A psychometric model for scaling ability and diagnosing misconceptions.Psychometrika, 79, 403–425.

Cai, L. (2010). Metropolis-Hastings Robbins-Monro algorithm for confirmatory item factor analysis.Journal of Educational and Behavioral Statistics, 35, 307–335.

Chiu, C., Douglas, J., & Li, X. (2009). Cluster analysis for cognitive diagnosis: theory and applications.Psychometrika, 74, 633–665.

Chen, P., Xin, T., Wang, C., & Chang, H.-H. (2012). Online calibration methods for the DINA model with independent attributes in CD-CAT.Psychometrika, 77, 201–222.

Chalmers, P., Pritikin, J., Robitzsch, A., Zoltak, M., Kim, K.,Falk, C. F., & Meade, A. (2015).mirt: Multidimensional Item Response Theory. R package version 1.14, URL http://CRAN.R-project.org/package=mirt

de la Torre, J. (2009). DINA model and parameter estimation:A didactic.Journal of Educational and Behavioral Statistics,34, 115–130.

de la Torre, J. (2011). The generalized DINA model framework.Psychometrika, 76, 179–199.

de la Torre, J., & Douglas, J. (2004). Higher-order latent trait models for cognitive diagnosis.Psychometrika, 69, 333–353.

Ding, S. L., Yang, S. Q., & Wang, W. Y. (2010). The importance of reachability matrix in constructing cognitively diagnostic testing.Journal of Jiangxi Normal University (Natural Sciences Edition), 34, 490–494.

[丁树良, 杨淑群, 汪文义. (2010). 可达矩阵在认知诊断测验编制中的重要作用.江西师范大学学报(自然科学版),34, 490–494.]

Embretson, S. E., & Yang, X. D. (2013). A multicomponent latent trait model for diagnosis.Psychometrika, 78, 14–36.

Junker, B. W., & Sijtsma, K. (2001). Cognitive assessment models with few assumptions, and connections with nonparametric item response theory.Applied Psychological Measurement, 25(3), 258–272.

Henson, R. A., Templin, J. L., & Willse, J. T. (2009). Defining a family of cognitive diagnosis models using log-linear models with latent variables.Psychometrika, 74, 191–210.

Huang, H. Y., & Wang, W. C. (2014). The random-effect DINA model.Journal of Educational Measurement, 51,75–97.

Karelitz, T. M. (2004).Ordered category attribute coding framework for cognitive assessments(Unpublished doctorial dissertation). University of Illinois at Urbana– Champaign.

Leighton, J. P., Gierl, M. J., & Hunka, S. M. (2004). The attribute hierarchy method for cognitive assessment: A variation on Tatsuoka’s rule-space approach.Journal of Educational Measurement, 41, 205–237.

Li, X. M., & Wang, W.-C. (2015). Assessment of differential item functioning under cognitive diagnosis models: The DINA model example.Journal of Educational Measurement, 52,28–54.

Maris, E. (1999). Estimating multiple classification latent class models.Psychometrika, 64, 187–212.

R Core Team. (2015).R: A language and environment for statistical computing(Version 2.15.1) [Computer Software].Vienna, Austria: R Foundation for Statistical Computing.Available from http://www.R-project.org/

Reckase, M. (2009).Multidimensional item response theory.New York: Springer.

Robitzsch, A., Kiefer, T., George, C. A., & Uenlue, A. (2015).CDM: Cognitive Diagnosis Modeling. R package version 4.6-0, URL http://CRAN.R-project.org/package=CDM

Stout, W. (2007). Skills diagnosis using IRT-based continuous latent trait models.Journal of Educational Measurement,44, 313–324.

Sun, J., Xin, T., Zhang, S. M., & de la Torre, J. (2013). A polytomous extension of the generalized distance discriminating method.Applied Psychological Measurement,37, 503–521.

Tatsuoka, C. (2002). Data analytic methods for latent partially ordered classification models.Journal of the Royal Statistical Society: Series C (Applied Statistics), 51, 337–350.

Tatsuoka, K. K. (1983). Rule space: An approach for dealing with misconceptions based on item response theory.Journal of Educational Measurement, 20, 345–354.

Templin, J., & Bradshaw, L. (2013). Measuring the reliability of diagnostic classification model examinee estimates.Journal of Classification, 30, 251–275.

Templin, J., & Bradshaw, L. (2014). Hierarchical diagnostic classification models: A family of models for estimating and testing attribute hierarchies.Psychometrika, 79, 317–339.

von Davier, M. (2005).A general diagnostic model applied to language testing data(ETS Research Report no. RR-05-16).Princeton, NJ: Educational Testing Service.Wang, C., Chang, H.-H., & Huebner, A. (2011). Restrictive stochastic item selection methods in cognitive diagnostic computerized adaptive testing.Journal of Educational Measurement, 48, 255–273.Wang, C., & Nydick, S. W. (2015). Comparing two algorithms for calibrating the restricted non-compensatory multidimensional IRT model.Applied Psychological Measurement, 39, 119–134.

Zhan, P. D., & Bian, Y. F. (2015). The probabilistic-inputs,noisy “and” gate model.Psychological Science, 38, 1230–1238.

[詹沛达, 边玉芳. (2015). 概率性输入, 噪音“与”门(PINA)模型.心理科学, 38, 1230–1238.]

Zhan, P. D., Bian, Y. F., & Wang, L. J. (2016). Factors affecting the classification accuracy of reparametrized diagnostic classification models for expert-defined polytomous attributes.Acta Psychologica Sinica, 48, 318–330.

[詹沛达, 边玉芳, 王立君. (2016). 重参数化的多分属性诊断分类模型及其判准率影响因素.心理学报, 48, 318–330.]

Zhan, P. D., Li, X. M., Wang, W.-C., Bian, Y.-F., & Wang, L. J.(2015). The multidimensional testlet-effect cognitive diagnostic models.Acta Psychologica Sinica, 47, 689–701.

[詹沛达, 李晓敏, 王文中, 边玉芳, 王立君. (2015). 多维题组效应认知诊断模型.心理学报, 47, 689–701.]

Zhan, P. D., Wang, W.-C., Bian, Y. F., & Li, X. M. (2016).Higher-order cognitive diagnostic models for polytomous latent attributes. Paper presented at the annual meeting of the National Council on Measurement in Education,Washington, DC.

Zhan, P. D., Wang, W.-C., Li, X. M., & Bian, Y. F. (2016).The probabilistic-inputs, noisy conjunctive model for cognitive diagnosis. Paper presented at the annual meeting of the American Educational Research Association, Washington,DC.

附录：模拟研究参数估计程序(以K=3、I=15为例)

1 LLM

R> library (CDM) #载入CDM包

R> Qmatrix <- read.table ("Q3.txt") #读取Q矩阵

R> Data <- read.table ("data.txt”) #读取作答数据

R> LLM <- gdina (data=Data, q.matrix=Qmatrix, rule="ACDM", linkfct="logit") #ACDM与LLM差异在于连接函数不同

R> attribute <- IRT.factor.scores (LLM, type="MAP") #读取被试属性估计值, 选用MAP方法

R> itempar <- LLM $ coef [, c (1,2,3,6,7) ]) #读取题目参数估计值, 原文未呈现

R> summary (LLM) #输出诸如参数估计数量、模型-数据拟合指标、属性相关等信息

R> IRT.modelfit (LLM) #输出模型-数据拟合指标, 如SRMR、AIC、BIC等

2 CC-M2PLM

R> library (mirt) #载入mirt包

R> K<-3 #设定维度数

R> Q <- matrix(scan("Q3.txt"), ncol=K, byrow=T, dimnames=list(NULL, c('Factor1', 'Factor2', 'Factor3'))) #读Q矩阵, 维度赋名

R> cc <- 1 - diag(K)

R> COV <- as.matrix(cc==1) #设定维度之间存在相关, 用于参数估计

R> model <- mirt.model(Q, COV=COV) #依据Q矩阵, 来界定题目与维度之间的关系

R> Data <- read.table("data.txt”) #读取作答数据

R> CM2PLM <- mirt(data=Data, model=model, method="MHRM", SE=T) #选用MHRM法进行参数估计

R> theta <- fscores(CM2PLM, method="MAP", full.scores.SE=T) #读取被试潜在特质估计值, 选用MAP方法

R> itempar <- coef(CM2PLM, as.data.frame=T, SE=T) #读取题目参数估计值, 原文未呈现

R> M2(CM2PLM) #输出模型-数据绝对拟合指标, 如M2、SRMR、RMSEA等

R> print(CM2PLM) #输出模型-数据相对拟合指标, 如AIC、BIC等

R> CP<- c ( 0, 0, 0) #设定3个维度的切点均为0

R> tb.attribute <- theta

R> for ( k in 1:K) {tb.attribute [ , k ] <- ifelse ( theta [ , k ] > CP [ k ], 1, 0 )} #将潜在特质估计值转换为跨界属性