交通流Washout缓解控制方案试验分析

任鹏飞，薛　鹏，李　可

(河南工程学院 电气信息工程学院，河南 郑州 451191)



交通流Washout缓解控制方案试验分析

任鹏飞，薛鹏，李可

(河南工程学院 电气信息工程学院，河南 郑州 451191)

摘要：针对环状交通流拥堵的问题，基于最优速度函数提出了Washout缓解控制方案.分析环状交通流的行进特点，建立系统动态平衡控制模型后，再利用乐高NXT模型车搭建室内试验平台.设定运行时间为5 min，定点监测车流密度和流量变化.将试验数据与实测交通数据进行对比，验证了模型的有效性.进一步为被控车流引入Washout控制器，试验数据显示该方案可有效缓解交通阻塞，在拥堵形成初期的控制效果尤为明显.

关键词：交通拥堵；车流密度；不稳定平衡；最优速度

在交通流优化控制问题中，流量、速度和密度是主要指标.车流从顺畅的自由流向拥堵的阻塞流转变时，会出现流量急剧减少的现象[1-2].如何降低观测点车流量的减少速度，是缓解交通拥堵、提高出行质量亟待解决的问题之一.

控制交通流以缓解阻塞最理想的方案就是使全部车辆自动行驶，但全自动行驶技术在安全等方面还存在很多问题.已有不少文献对缓解拥堵的策略在理论和试验的多个层面进行了探讨，如文献[3] 针对解决城市交通拥堵决策问题，从错误优化的角度来研究城市交通拥堵的决策方法；文献[4]针对紧急交通流优先控制对城市常态交通干扰导致的拥堵问题，提出了一种面向紧急交通流分级优先控制的优先级划分模型；文献[5]基于Washout控制方法针对环状交通流中因车辆加减速度控制不当引起的交通不畅问题，分析了控制器的有效性和参数控制条件.在此基础上，进一步研究了Washout控制的可行性，提出了在每辆车上加载驾驶辅助控制系统来协助司机调节车速以实现交通流的阻塞抑制，并构建了乐高NXT小车进行室内试验，以验证方案的有效性.

先采用最优速度函数建立模型车交通流的动态数学模型.试验侧重两方面：一是通过与实际车流数据的对比来验证模型的有效性，二是基于模型提出加载于各个车辆的Washout控制.通过对比分析控制器加载前后的车流运行特征，分阶段指出了控制器的优化效果.

1交通流动态模型

司机驾驶车辆时，需要根据与前方车辆的距离和自己当前的车速调节控制速度.理论上的最优速度函数是车速控制的理想状态.在不过度干涉司机驾驶意图的前提下，以车速协助调节，以实现每辆车都维持最佳车速行驶.最优速度函数采用

(1)

式中：yi表示第i辆车的车头与第i-1辆车的车尾之间的距离；b，c，yc是确定最优速度的必要参数.

1.1　试验小车状态模型

采用乐高NXT小车进行室内试验.当以最优速度函数调节车速时，第i辆车的驱动电压满足

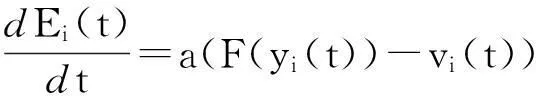
(2)

式中：Ei是小车电机输入电压，vi是第i辆车的速度，参数a表征司机对油门/刹车的控制灵活度.采用超声波传感器测定车距，以光栅传感器测定车速，可得动态车流速度模型为

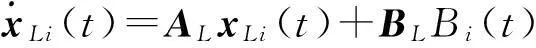
(3)

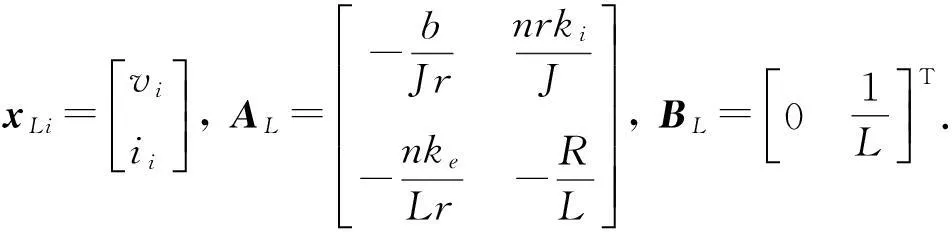
由式(2)、(3)可得第i辆车的状态模型为

(4)

1.2　最优速度Washout控制

实现车速遵循最优速度函数以缓解交通拥堵问题是系统设计目标.但是，控制速度和车距到哪个具体值是很难用函数准确描述的.也就是说，系统的平衡点是不确定的.如何在不确定的平衡点实现系统的稳定控制是关键问题.Washout控制可基于最优速度函数实现车流速度在系统平衡点的稳定控制.

假设在长度为C的环形车道上共有N辆车在行驶，平衡状态下的车间距离应满足

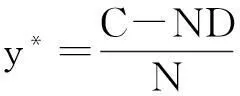
(5)

车辆速度应满足

(6)

同时，第i辆车的控制电压满足

(7)

给第i辆车添加Washout控制器

(8)

式中：α和 β均不为0，选择两者的适当值，使得系统稳定到平衡点来抑制阻塞.

添加控制器(8)，通过式(4)和式(7)进行稳定性分析.在车流系统平衡点处有

(9)

(10)

B=[01000]T. 其中，Λ是平衡点y=y*处最优速度函数的变化率，即

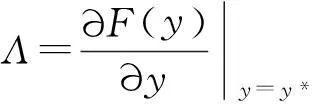
(11)

进一步考虑环形车道的圆周特点，有

(12)

又因为

(13)

所以，系统应满足约束条件

(14)

在使用Washout控制器后，车距yi和车速vi应满足

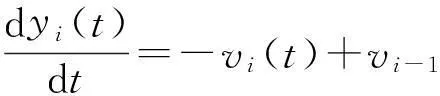
(15)

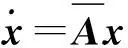
(16)

系统(16)存在一个零特征值，但由于约束条件(14)，这个零特征值对应的特征向量正好是系统的一个平衡状态.因此，若要使系统(16)闭环稳定，只要矩阵A的非零特征值全部具有负实部即可.因此，可以确定Washout控制器的关键参数α和β.

2验证与分析

以环状车流为研究对象，借助乐高NXT模型车进行室内试验，现场如图1所示.重点分析两个问题：一是将试验结果和实测车流数据进行比对,分析所建模型的可靠性；二是引入控制器(8)分析Washout控制抑制或缓解交通阻塞的有效性.

图1　试验现场俯视图Fig.1　Top view of the laboratory experiment

2.1　可靠性分析

假定共有N台车按照逆时针方向行驶在环形车道上，所有车辆长度均为D.为简化模型，进一步假设所有车辆拟遵循的最优速度控制参数相同，全部车辆都采用a=0.15,b=7,c=7,yc=20的参数设置.如图1所示，直径为2 m的环形车道上共放置了7台车，行车时间设定为5min，所测得的车流量和车流密度的关系如图2所示.

图2　无控制车流特性Fig.2　Traffic flow without control

从图2可以看出，车流特征依照密度明显分为两部分：在低密度区段，车流顺畅通行，车流密度稍增加，车流量也随之增加，此时，车流以一定速度前进，为自由车流；在高密度区段，阻塞现象出现，车流密度的增加反而导致车流量减少，为阻塞流.这两种状态以一定的车流密度为界限发生明显转变,与文献[2]的数据对比可知，这一结果和现实中的车流变化完全一致，验证了模型的合理性和有效性.

2.2　优化效果分析

为了控制交通流的流量变化，给全部车辆安装Washout控制器(8)，选择控制器参数α=-5,β=0.5,所得的运行结果如图3所示.从图3中可以看出,在车流密度ρ为0~2.5台/m的低密度区段时，施加控制和不施加控制的结果完全相同，车流在这个阶段都按照最优速度函数以一定速度行驶.在ρ为2.5~2.9台/m的交替阶段时，车流量较大，在没有施加控制的自由行驶状态下，车流量急剧下降，而施加Washout控制的情况下就没有这种现象.在ρ=2.9台/m以后，车流处于严重拥堵状态，控制失效.

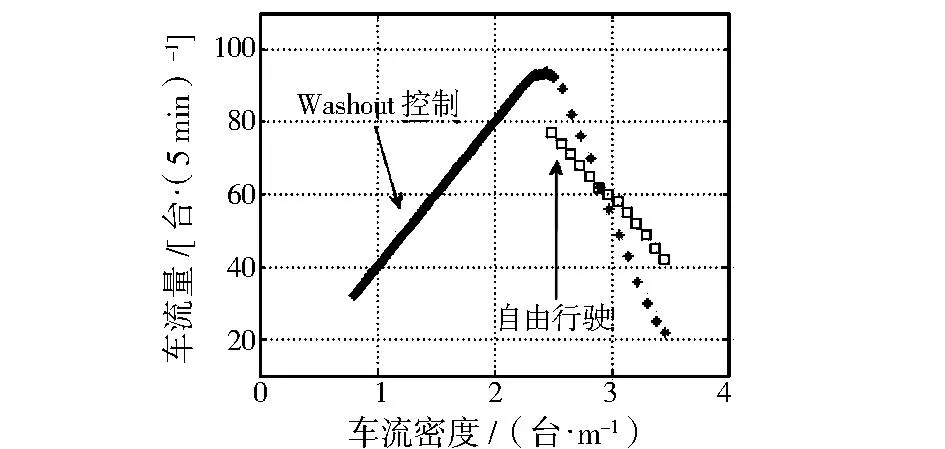
图3　Washout控制效果Fig.3　Traffic flow with Washout control

由此可见,在Washout控制下，车流在从自由流向阻塞流转变阶段，交通阻塞缓解，可抑制车流量急剧减少的现象；在车辆低密度行驶时，同样能保障车流以最优速度行驶；在车流严重拥堵时，控制是无效的.

进一步从车间距离分析车流阻塞抑制效果.图4以各车的车头距第一台车车头的距离为参考指标，对比分析所提的控制方案对车流运行特征的改进效果.在车流阻塞形成初期，7台车直接的车距如图4(a)所示，随时间波动的车距显示了车流的阻塞状态.在引入Washout控制方案后，车间距如图4(b)所示.可以看出，各车辆等间距前进，车辆能保持最优速度行驶.对比可见，所提控制方案是有效的.

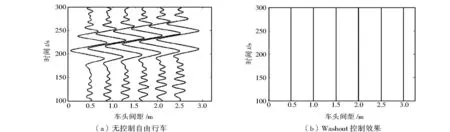
图4　车头间距仿真分析Fig.4　Simulation results of space headway

3结语

借助最优速度函数构建了环状交通流的动态模型.首先，利用乐高NXT模型车进行室内试验，以所建模

型和实际车流具有相同特性的结果验证了建模的合理性和有效性.然后，给车辆添加Washout控制器，结果显示车流阻塞带来的车流量减少现象得到了抑制，交通效率进一步提高.不足的是，所有车流都遵从同一最优速度函数的假设不尽合理，在今后的研究中应进一步完善.

参考文献:

[1]GE H X,YU J,LO S M.A control method for congested traffic in the car following model[J].Chinese Physics Letters,2012,29(5):500-502.

[2]廖律超，蒋新华，邹富民,等.基于交通视频的交通拥堵状态自动识别方法[J].公路交通科技，2014，31(1):110-117.

[3]周金革，叶启新，郭开仲.基于错误矩阵方程的解决城市交通拥堵决策研究[J].数学的实践与认识，2014,44(1)：163-169.

[4]王嘉文，马万经，杨晓光.紧急交通流信号控制优化级划分模型[J].东南大学学报：自然科学版，2014,44(1)：222-226.

[5]薛鹏，任鹏飞，王划.环状交通流Washout控制及其稳定性分析[J].计算机应用,2014,34(2)：597-600.

Experimental investigation of effects of Washout control

on reducing traffic jam

REN Pengfei, XUE Peng, LI Ke

(CollegeofElectricalInformationandEngineering,HenanInstituteofEngineering,Zhengzhou451191,China)

Abstract:Aiming at issues of traffic jams in circle, Washout out control scheme was proposed based on optimal velocity functions. Dynamic balancing control system model was established after analyzing the characteristics of cyclic traffic flows. Then indoor experimental platform was constructed with LEGO robot cars. Traffic flow and density were collected at a given position in 5 minutes. Comparing experimental results with real traffic data, the effectiveness of the model was validated. Introducing Washout controller for each vehicle, the data showed that the Washout control scheme can release the traffic jams and the control effect is particularly significant in the early stage of congestion.

Key words:traffic jam；traffic density；unstable balancing；optimal velocity

作者简介：任鹏飞(1982-)，男，河南郑州人，讲师，主要从事自动化设备应用方面的研究.

收稿日期：2015-09-08

中图分类号：TM343

文献标志码：A

文章编号：1674-330X(2015)04-0059-04