基于基准的定位元件约束自由度分析

赵轲

(广东石油化工学院 机电工程学院，广东 茂名 525000)

基于基准的定位元件约束自由度分析

赵轲

(广东石油化工学院 机电工程学院，广东 茂名 525000)

摘要：为解决工件在定位时需要约束的自由度数和自由度以及定位元件约束工件自由度数和自由度的问题，应用六点定位原理，对各种典型定位实例和定位元件进行了分析。分析表明，工件需要约束的自由度数和自由度由所选择的定位基准几何特征决定，而定位元件约束的自由度数和自由度也由定位元件与定位基准实质接触面几何特征来决定，且其个数都遵循“面三、线二、点一”的规律。

关键词：定位基准；自由度；约束；定位元件

Analysis of DOF Constrained by Position-Element Based on Datum

ZHAO Ke

(College of Machinery and Electronic Engineering, Guangdong University of Petrochemical

Technology, Maoming 525000, China)

Abstract:In order to solve the problems of DOF and DOF number which needs to be constrained when the workpiece is located, and position-element can constrain, this paper analyzes the cases of typical position and position-elements. It indicates: DOF and DOF number which needs to be constrained is determined by the geometric features of location datum, DOF and DOF number which the position-element can constrain is determined by the geometric features of essence contact surface between the position elements and the location datum, the DOF number is three, two and one when the datum and contact surface is surface line and point.

Keywords:location datum; DOF; constraint; position-element

0引言

工件在夹具中定位，以便相对于机床和刀具有正确的位置进行加工，所以，定位方案需要约束的自由度，应根据工件被加工面的加工要求来决定。一般来讲，根据6点定位原理，工件在空间运动的6种可能性，即6个自由度，应该用6个正确分布的点来全部约束。但事实上，不是所有的被加工工件都需要约束6个自由度，进行6点完全定位，也可以采用不完全定位和过定位方案等。甚至，有些工件是无法进行完全定位的。文中对各种典型的工件定位实例进行分析，同时研究了典型定位元件约束了工件的自由度，揭示了工件需要被约束的自由度数、自由度与选用的定位基准几何特征之间的内在联系和基本规律，为合理设计定位方案和选择定位元件提供了直接的理论依据。

1定位基准与约束自由度和自由度数的关系

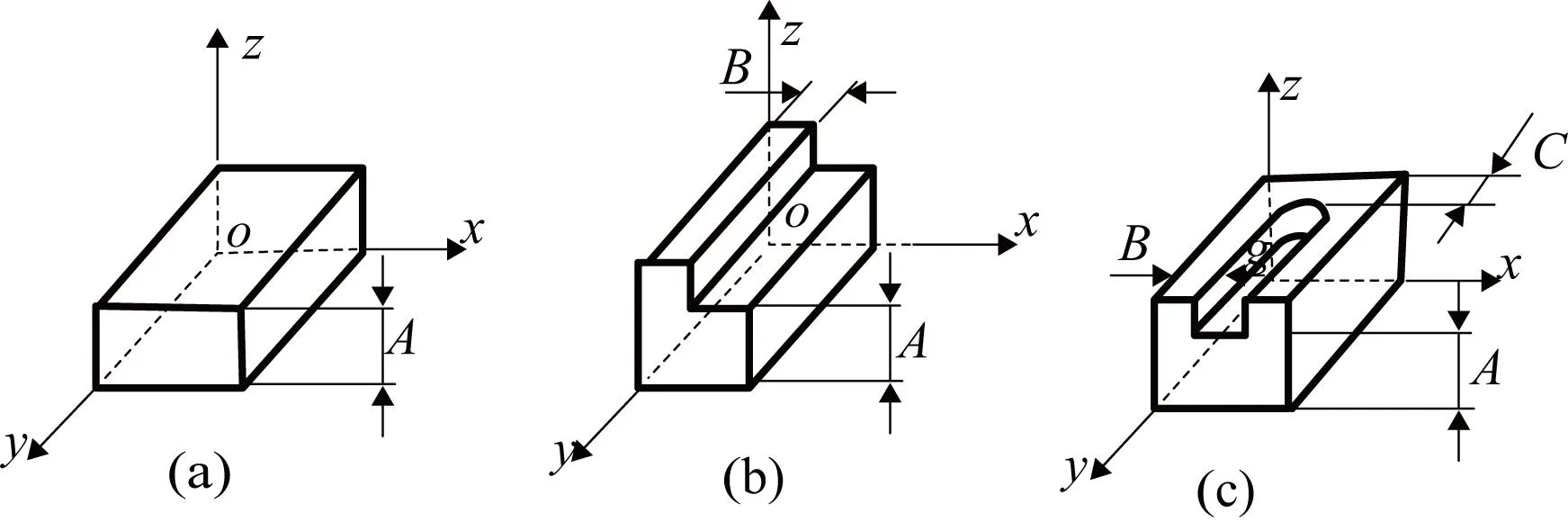
图1　长方体工件的定位基准

图2　长圆柱体工件的定位基准

图3　球体工件的定位基准

综上所述，在判断工件需要约束哪些自由度时，可根据其尺寸精度要求，先确定需要的定位基准面，并根据所选的定位基准面几何特征，遵循“面三、线二、点一”的规律来确定各自需要约束的自由度数和自由度，然后根据实际情况，考虑需要消除的重复定位，即可得到工件需要约束的自由度。

2定位元件约束的自由度数

确定需要约束的自由度后，需要选择合适的定位元件对工件进行定位，而定位元件能够限制的自由度，也由定位元件的定位面几何特征来决定。

常用的定位元件主要有：支承钉(如图4(a))，支承钉与定位基准面的接触本质上相当于一个点，限制一个自由度；支承板，短V型块，短定位套、短定位销等(如图4(b))与定位基准面的接触本质上相当于一条线，限制两个自由度；锥套和锥销(如图4(c))与定位基准面的接触为面，限制3个自由度。从表面上看，锥销和定位基准面的接触为线接触，但其定位元件的定位面为锥面，和平面定位一样，故其应限制3个自由度。具体限制哪些自由度，不再赘述。

图4　常用的定位元件

综上所述，定位元件限制的自由度数也遵循“面三、线二、点一”的规律，这里的面指与定位元件实际接触的定位面是圆锥面或者大的平面。

3结语

工件在夹具中定位时，需要约束其在空间中运动的6种可能性，即6个自由度。但在分析定位需要约束的自由度时，需要注意“定位不等于夹紧”等问题。因为概念不明确，难以区分析并得出到正确的结论，或者得到正确的结论但不明白为什么。

文中从定位基准的角度出发，分析了6点定位原理，明确了定位就是通过确定定位基准面在空间(夹具中)的正确位置，进而使得工件定位的概念。所以，选择不同的几何要素做基准面，只要分析该几何要素在空间需要约束的自由度就可以了，且该自由度数也是基准面最多能约束的自由度数，遵循“面三、线二、点一”的规律(不包括出现过定位时的分析[4])。定位元件限制的自由度数由定位元件的有效作用面形状决定，也遵循“面三、线二、点一”的规律。

参考文献:

[1] 吕明，庞思勤. 机械制造技术基础(第2版)[M]. 武汉：武汉理工大学出版社,2010.

[2] 吴拓. 机械制造工艺与机床夹具[M]. 北京: 机械工业出版社,2010.

[3] 李邵华. 数控机床与工装夹具设计[M]. 杭州：浙江科学技术出版社,2009.

[4] 严红. 组合定位时自由度判定的研究与应用[J] . 湖南工业职业技术学院学报，2012，8(4)：36-37.

收稿日期：2014-05-06

中图分类号：TH703.65

文献标志码：B

文章编号：1671-5276(2015)04-0067-02

作者简介：赵轲(1978-)，女，山西兴县人，讲师，硕士，研究方向：机电液一体化产品设计。

基金项目：茂名市科技计划项目资助 (2011B01008)