稀疏阵列相干信号功率合成栅基仿真技术

陈秋菊，姜秋喜，曾芳玲，王华山

(1. 电子工程学院 信息处理重点实验室，　合肥 230037)

(2. 桂林长海发展有限责任公司，　广西 桂林 541001)



稀疏阵列相干信号功率合成栅基仿真技术

陈秋菊1，姜秋喜1，曾芳玲1，王华山2

(1. 电子工程学院 信息处理重点实验室，合肥 230037)

(2. 桂林长海发展有限责任公司，广西 桂林 541001)

摘要：稀疏阵列相干信号功率合成栅基仿真技术包括阵列功率合成数学建模、栅格尺度原则选定及计算机仿真实验设计实现等。文中从多点源稀疏阵列交汇区域相干信号的功率合成原理出发，建立其数学模型，设计了栅基实验流程，并对实验中重要参数栅格尺度的选定原则进行了推算分析，为利用计算机无失真地复现多点源功率合成能量分布规律打下了理论基础。

关键词：稀疏阵列; 空间功率合成; 相干信号

0引言

当前空间功率合成技术多采用集中密布阵方式[1-7]，合成出的波束中心指向天线阵，形成以目标方向为中心的扇形区域，易被敌方准确测向定位，其抗反辐射导弹攻击能力较弱。随着相控技术的发展，稀疏多点源各信号之间相位相干逐渐成为可能[8]。稀疏分布多点源通过干涉效应在交汇区域实现功率增强，可在扩大电子干扰威力的同时，以分散布阵的方式使对方侦察测向设备不能对其测向定位，利于隐蔽自身，能够有效对抗反辐射武器，增强系统的生存能力。

文献[9]就二元稀疏阵的交叉波束合成进行了初探，经过分析得出两交叉波束的工作波长越短，则交汇区域内干涉相长点越密；两波束交叉角度越大，干涉相长点也越密的结论。文献[10]也就频率、极化方式等因素对二元阵列的功率合成效果的影响进行了初步分析。当点源数增加后，复杂性也大大提高,但文献中并没有给出进一步的分析和讨论。文献[11]讨论了相位的随机性对空间目标点功率合成的影响，但只分析了相干信号交汇区域内其他点的功率分布。本文提出基于计算机仿真的相干信号功率合成栅基仿真技术，建立了多点源交汇区域相干信号功率合成数学模型，研究了多点源在交汇区域的干涉效应仿真中的栅格尺度选择问题，为无失真地复现多点源功率合成能量分布规律打下理论基础。

1多点源交汇区域相干信号功率合成数学模型

建立大地直角坐标系，如图1所示。以正北方向为Y轴，正东方向为X轴，设T为目标点，其坐标为T(x0,y0,z0)，各点源位置为Ai(xi,yi,zi)，i=1,2,…,N(N≥3)，N为节点数。各点源波束均指向目标点，H为交叉波束交汇区域内另一点，其坐标为H(x,y,z)，各站发出的信号频率相同，通过对各节点信号相位的控制，使在点T的场强得到增强。图1中，r、r′分别为T点和H点到原点的距离，Rit为第i个节点到T点的距离，Ri为第i个节点到H点的距离。

假设第i个点源发出的信号在T点产生的场强为

(1)

图1点源及区域点的空间位置图

(2)

各节点到达H点的相位为φi，则

(3)

则H点总合成场强为各方向合成场强分量的矢量叠加，即有

(4)

其中

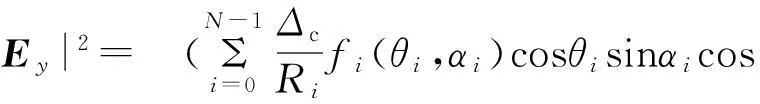
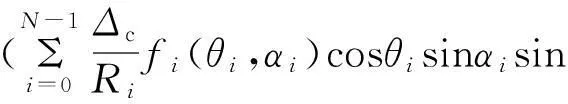
于是得

|Eh|2=|Ex|2+|Ey|2+|Ez|2=

cos(φi-φj)[cosθicosθjcos(αi-αj)+

sinθisinθj])

(5)

由于电磁波的传播和干涉效应，当H点位于交叉区域内不同位置时，合成功率值是不同的，该值受到各点源与H点之间的方位因素的影响。

各节点信号到达目标参考点T时，由于在初相设置中，已包含为抵消波程而设置的相位。因此，信号达到T点时，相位经波程抵消后可视为0或固定值φ0，则可得在T点的合成场强的平方值为

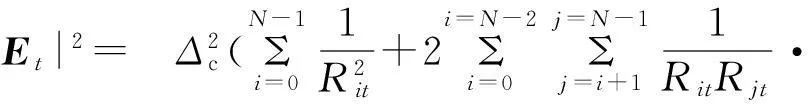
[cosθicosθjcos(αi-αj)+sinθisinθj])

(6)

可见，通过相位控制，可使各站发射的信号到达T点的场强同相，使T点的功率合成仅依赖于节点与目标点之间的几何位置关系。

2栅基仿真技术

由式(5)可知，当点源数大于2时，难以对交汇区域中各点功率分布规律进行理论探讨。为便于分析，拟采用计算机栅基仿真实验，即对稀疏阵的空间交汇区域按一定间隔划分栅格，进行采样，对每个采样点基于式(5)进行合成场强计算，进而得到各点功率值，以便观察和分析合成功率分布。

图2栅基实验分析流程

栅基实验分析流程，如图2所示。

为了精细描述区域内功率分布，采样间隔(即栅格尺度)应尽可能小。但考虑到计算量的限制，采样间隔不可能无穷小。采样间隔的选择与波束干涉相长点分布规律有关。首先就二元稀疏阵交叉波束合成进行初步分析，如图3所示。

图3　两点源稀疏阵交叉波束合成示意图

设S1、S2构成二元稀疏阵，A为目标点，针对目标点S1、S2波矢方向分别为k1和k2，α、β分别为天线S1和S2天线主方向的倾斜角。假设两波束均为线极化，极化方向相同，则两天线对准目标点时，两相位相长点之间的间距为[3]

(7)

下面将从式(7)出发，推算栅基仿真实验中栅格尺度的选定原则。

二元稀疏阵的波束交叉区域中，取任一点(如A点)为参考起点，则其在任意某一方向(如γ角方向)的等相位相长点将周期性出现，等相位相长点A点与其γ角方向最邻近的等相点B点的距离L为

(8)

则该方向上其他等相位相长点与A点的间距为L的整数倍，即等相位相长点出现周期为

(9)

研究合成功率分布时，需重点关注区域内能量相长的情况，不希望在仿真过程中遗漏相长点。因此，采样时栅格尺度应能够满足反映相长点分布规律的要求。而相对于参考点A点，γ角方向等相位相长点出现频率为

(10)

由奈奎斯特采样定律可知，如需无失真保留该方向相长点分布规律，则该方向采样频率fs需满足fs≥2fL，即

[2]Bandekar, B.V. and S. Singh, System and method to provide analytical processing of data in a distributed data storage systems. 2017.

(11)

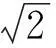
(12)

(13)

对于多元稀疏阵，进行二维栅基实验时采样间隔应满足如下条件

(14)

可知

(15)

进行三维栅基实验时采样间隔应满足如下条件

(16)

可知

(17)

3基于有效功率区的栅基尺度选定原则校验

在多点源情况下研究空间功率合成，感兴趣的是信号叠加到超过一定阈值的有效功率点分布的情况。但由于节点多，叠加情形复杂，难以如二元情形推算出相长点的分布情况，除目标参考点外，所有节点信号完全同相的叠加点可能并不存在。因此，定义有效功率点的概念，根据T点和H点的功率关系，将满足|Eh|2/|Et|2≥γ0的H点视为有效功率点，其中|Et|2按式(6)取最佳合成时的功率值。

γ0的取值根据实际需要确定，将满足上述不等式的点标定出构成多点源交叉区域内的有效功率点。有效功率点聚集的区域叫做有效功率区，有效功率区的数量和分布往往是重点关注区域。考虑到空间功率干涉合成的应用需求，我们基于有效功率区分布特征(如数目、位置)进行栅基仿真技术的二维校验实验。实验如下：

实验条件：稀疏阵列阵型选择，如图4a)所示。

图4　一种阵型示意图(目标处为[0，0])与各节点天线方向图

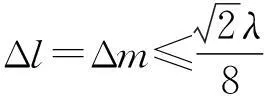
表1各次实验栅格尺度设定值m

观察区域x轴方向[-2.5m,2.5m]，y轴方向[-2.5 m,2.5 m]。结合功率合成分析的应用需求，仿真校验采用有效功率区个数及分布进行衡量。各次实验结果见图5，有效功率区个数见表1，为便于观察，我们对有效点分布图中非有效点的灰度值进行了置零处理。

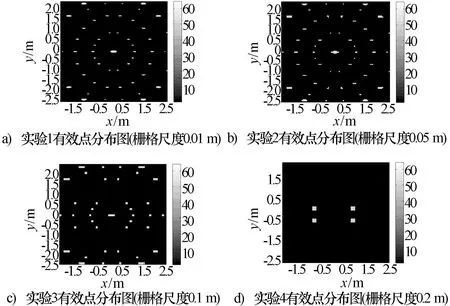
图5　各次实验仿真结果图

综上所述，推算出的尺度要求，栅格尺度不得小于0.053 m。实验1、实验2均满足该要求，则从表1中有效功率区个数及图5中有效点分布可见，仿真结果仍能真实反映有效功率块状区的分布情况，失真不明显；实验3、实验4均不满足该要求，结果在有效功率块状区数目以及有效点占比等指标上严重失真。该实验有效验证了栅格尺度的选定原则。

4多点源稀疏布阵功率合成仿真案例

选用两种阵型进行多点源稀疏布阵功率合成仿真实验。除阵型外，其他实验条件均与第3节中栅格尺度选定原则验证实验相同。栅格尺度：Δx=Δy=0.05 m。单线阵阵型如图6a)所示：各节点在二维平面内等间距分布于距离目标中心点[3 km,5 km]区间，波束中心均对准目标点([0,0])。双线型阵型如图6b)所示：各节点在二维平面内等间距分布于距离目标中心点[3 km,5 km]区间内且与目标中心点共线的两条线上，波束中心均对准目标点([0,0])，其中一条线与x轴正向夹角60°，另一条线与x轴正向夹角120°。观察区域x轴方向[-100 m, 100 m]，y轴方向[-100m, 100m]。

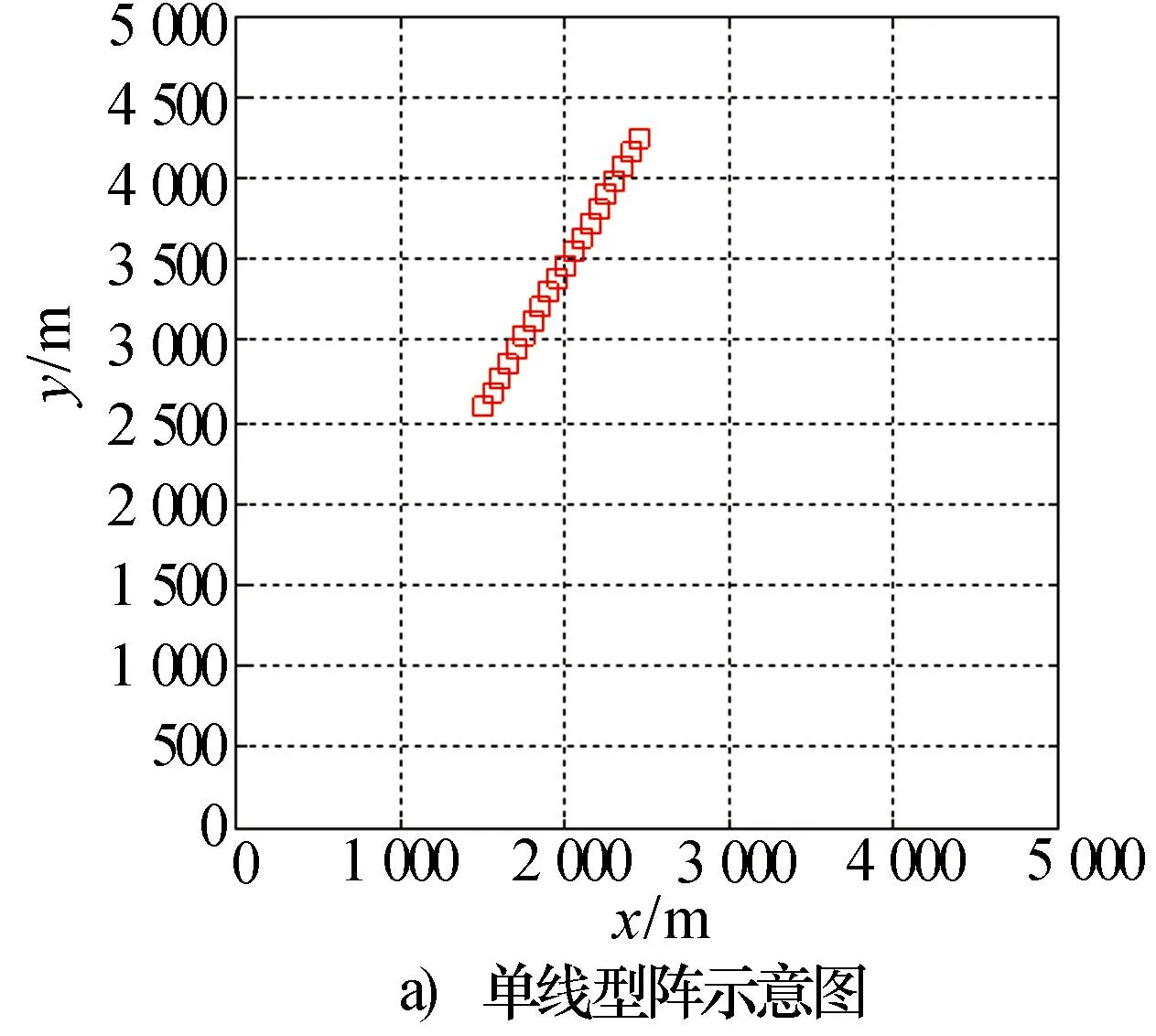
图6　阵型示意图

单线型阵功率合成效果如图7a)、图7b)所示。双线型阵功率合成效果如图7c)、图7d)所示。

5结束语

当点源数量较大时，稀疏阵列空间功率合成难以仅仅依靠理论模型进行分析，必须通过计算机进行仿真实验加以研究。本文结合相干信号功率干涉合成的理论模型及相长点分布规律，讨论了计算机栅基仿真技术中重要的指标选定原则，即栅格尺度的选定原则，并通过实验进行了初步验证，并给出了典型阵型下的干涉合成结果。下一步还将借助图像的结构相似度指标加以验证，并进一步研究不同阵型的合成功率分布规律。该文可为多点源稀疏阵列空间功率合成的仿真研究提供理论依据。

参 考 文 献

[1]邓朝平，侯德亭,周东方, 等. 密集阵高功率微波空间功率合成[J]. 强激光与粒子束，2013, 25(2): 436-441.

Deng Chaoping, Hou Deting, Zhou Dongfang, et al. Spatial power combing of close-packed antenna arrays of high power microwave[J]. High Power Laser and Particle Beams, 2013, 25(2): 436-441.

[2]葛俊祥. 毫米波空间功率合成技术及其发展[J]. 电子学报, 1995, 23(10): 152-154.

Ge Junxiang. Millimeter wave spatial power combine technqiue and its advance[J]. Acta Electronica Sinica, 1995, 23(10): 152-154.

[3]张光义. 相控阵雷达系统[M]. 北京: 国防工业出版社, 2000.

Zhang Guangyi. Phased array radar system[M]. Beijing: National Defense Industry Press, 2000.

[4]Liu W, Zhou H J, Luo X G. Combined efficiency analysis of spatial power combining[C]// 2012 IEEE 11th International Conference on Signal Processing. Xi′an, China: IEEE Press, 2012: 333-337.

[5]Varia K R. Power combining in a single multiple-diode cavity[C]// IEEE MTT-S International Microwave Symposium Digest. Ottawa, Canada: IEEE Press, 1978: 344-345.

[6]Ma Y, Sun C. 1-W millimeter-wave Gunn diode combiner[J]. IEEE Transactions MTT, 1980, 28(12): 1460-1463.

[7]胡风革, 张建华, 张尧锋. 基于改进遗传算法的反向天线阵稀疏优化[J]. 现代雷达, 2012, 34(5): 53-56.

Hu Fengge, Zhang Jianhua, Zhang Yaofeng. Optimization of sparse retrodirective array based on improved genetic algorithm[J]. Modern Radar, 2012, 34(5): 53-56.

[8]裴英, 肖文书. 相干MIMO雷达关键技术研究[J]. 现代雷达, 2013, 35(3): 9-12.

Pei Ying, Xiao Wenshu. A study on key technology of the coherent MIMO radar[J]. Modern Radar, 2013, 35(3): 9-12.

[9]张嘉焱, 舒挺, 袁成卫. 高功率微波空间功率合成的初步研究[D]. 长沙: 国防科学技术大学, 2006.

Zhang Jiayan, Shu Ting, Yuan Chengwei. Primary study on spatial powers combining of parallel and cross beams of high power microwave[D]. Changsha: National University of Defense Technology, 2006.

[10]路通. 空间功率合成中天线阵列的应用研究[D]. 成都: 电子科技大学, 2009.

Lu Tong. Research on synthesis of sparse volumetric array[D]. Chengdu: University of Electronic Science and Technology of China, 2009.

[11]任学尧, 陈鑫. 随机相位微波功率的空间合成效率[J]. 强激光与粒子束, 2009, 21(7): 1041-1004.

Ren Xueyao, Chen Xin. Efficiency of microwave power spatial synthesis under random phase shift[J]. High Power Laser and Particle Beams, 2009, 21(7): 1041-1044.

陈秋菊女，1982年生，博士。研究方向为信号与信息处理。

姜秋喜男，1960年生，教授，博士生导师。研究方向为电子对抗、信号与信息处理等。

曾芳玲女，1970年生，博士，副教授，硕士生导师。研究方向为电子对抗、电路与系统等。

The Grid-based Simulation for Power Synthesis of Sparse Array Coherent Signal

CHEN Qiuju1，JIANG Qiuxi1，ZENG Fangling1，WANG Huashan2

(1. Laboratory of Signal Processing, Electronic Engineering Institute,Hefei 230037, China)

(2. Changhai Co. Ltd of CEC,Guilin 541001, China)

Abstract：The grid-based simulation for power synthesis of sparse array includes power synthesis modeling, the sampling interval setting and realization of the computer simulation experiments. Based on the principle of power synthesis of sparse array, the mathematical model is established and the grid-based simulation experiment is designed. The setting principle of the most important parameter-sampling interval is analyzed. The results could be the theoretical basis for the further analysis of the space power synthesis of multi-source sparse array.

Key words：sparse array; power synthesis; coherent signal

收稿日期：2015-07-22

修订日期：2015-09-22

通信作者：陈秋菊Email：qqchern@gmail.com

中图分类号：TN957

文献标志码：A

文章编号：1004-7859(2015)11-0087-05