基于自适应系统辨识的收发隔离技术研究

邹纯烨，张剑云，周青松，黄中瑞

(合肥电子工程学院 雷抗系502教研室,　合肥 230037)



基于自适应系统辨识的收发隔离技术研究

邹纯烨，张剑云，周青松，黄中瑞

(合肥电子工程学院 雷抗系502教研室,合肥 230037)

摘要：收发隔离是机载干扰机不可避免的难题。如果收发隔离问题解决不好，轻则削弱干扰机效率，重则造成自发自收，形成自激励。固定步长的归一化最小均方误差(NLMS)算法在解决基于自适应系统辨识的收发隔离的问题时，由于精度不够，隔离效果很不理想。针对此问题提出一种基于先验误差的变步长NLMS算法，该算法依据相邻时刻先验误差的相关系数改变步长因子，改变后的步长因子能够在算法收敛过程中削弱噪声的影响，提高算法精度。理论分析和仿真结果证明：基于文中的变步长NLMS算法的收发隔离方案与基于其他最小均方误差算法的隔离方案相比，隔离性能有较大的改善。

关键词：收发隔离；自适应系统辨识；先验误差；归一化最小均方算法

0引言

有源干扰按干扰原理可分为压制性干扰和欺骗性干扰两类[1]。有源干扰机工作时，无论进行哪种类型的干扰，均必须随时对敌方雷达信号的参数进行侦察，然后根据侦察到的敌方雷达信号的参数，有针对性地调整干扰信号的频带范围和干扰功率分配。由于干扰机发射的干扰信号频率范围和接收端的频带范围有重叠，而且对于机载、舰载干扰机，发射机和接收机的空间距离受到限制。因此，发射机的大功率干扰信号不可避免会耦合到接收端。耦合到接收端的大功率干扰信号会增大接收机的外部噪声而使待跟踪目标信噪比降低，从而丢失目标信息；严重的情况下使干扰机自发自收，形成自激励[1]。解决干扰机收发隔离问题的一个有效方法是对收发耦合环境进行系统辨识，这样耦合到接收端的干扰信号能够通过辨识出的耦合系统提前预知，在接收端对消掉耦合干扰信号即能达到隔离的目的。为了研究方便，本文从时不变耦合环境入手。

针对时不变耦合系统下的收发隔离问题，文献[2]提出灵敏度-发射功率控制、时分隔离方案，优点是隔离度高，但是存在的不足是限制了发射端和接收端的同时工作，影响干扰机效率。针对此问题，文献[3-4]提出将自适应对消技术应用到收发隔离中，不足是未对隔离性能进行量化分析。文献[5]提出将收发耦合环境看成是时不变、小延时的，利用自适应最小均方误差(LMS)算法对耦合环境进行辨识，辨识后进行对消，达到隔离的目的。此隔离方案不仅可以隔离遮盖性干扰，而且可以隔离欺骗性干扰，但存在的问题是不能满足机载干扰机隔离度要求。

鉴于此，针对基于自适应系统辨识的收发隔离问题，本文提出一种新的基于先验误差的变步长归一化最小均方误差(NLMS)算法，应用此算法对耦合环境进行辨识能够取得比文献[5]所用方法更高的精度，因此可以获得更好的隔离性能。该收发隔离方法能够保证干扰机发射机和接收机的同时工作，并且为了增强说服力，本文对隔离性能进行了量化分析。

1问题描述

干扰机收发隔离是使干扰机发射机发射的干扰信号不影响接收机正常工作的问题。基于自适应系统辨识的收发隔离问题是指用自适应算法将收发耦合环境通路进行辨识，然后在接收端提前对消掉辨识干扰信号，从而达到收发隔离目的的问题。具体模型如图1所示。

图1　基于系统辨识的收发隔离模型

敌方雷达信号x(t)和干扰信号g(t)经过耦合环境产生的耦合干扰信号g′(t)同时进入侦察接收机，形成混合信号x(t)+g′(t)。由于耦合干扰信号g′(t)的功率较大而使敌方雷达信号x(t)淹没，收发隔离的目的就是将g′(t)削减为零(理想情况)，实际中g′(t)不可能为零。只要隔离后的信干比大于侦察接收机正常工作所需的信噪比即可。基于自适应系统辨识的收发隔离是指：利用输入数据g(t)和输出数据g′(t)加噪声，用自适应滤波算法将耦合通路h(t)辨识出来，辨识出的通路函数h′(t)称作辨识通路h′(t)，然后在接收端对消掉耦合的干扰信号。

为了研究方便，本文对耦合通路做两个合理化假设：(1)耦合通路在一段时间内是时不变的，即时不变耦合通路；(2)耦合通路主要由多径效应构成。干扰机发射端的干扰信号经过多条路径，每一条路径将延迟和衰减发射端的干扰信号到达接收端。这种情况下，可以证明逼近耦合通路函数h(t)的一个好的模型是低通节拍延迟线模型(FIR)[6]，如图2所示。

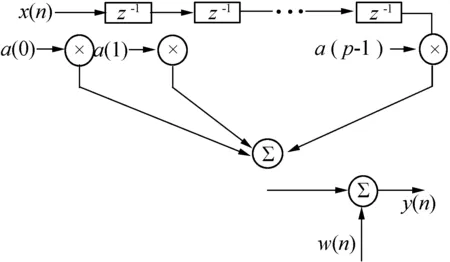
图2　节拍延迟线模型

耦合通路的时延和幅度衰减会在FIR模型的系数a(n)上反映，系统辨识的任务是根据输入信号x(n)和输出数据y(n)对系数a(n)进行估计。输入信号x(n)为用来进行自适应系统辨识的探测信号，理想情况下应该选择为伪随机信号[6]，但是实际中为实现方便常常选择高斯白噪声作为替代。自适应系统辨识算法有很多，但是，NLMS算法因其实现简单而应用最为广泛，是本文研究的重点。

2本文NLMS算法

2.1基本模型

假定d(n)为希望得到的滤波器输出信号，即

d(n)=xT(n)h(n)+v(n)=y(n)+v(n)

(1)

式中：xT(n)=[x(n),x(n-1),…,x(n-M+1)]T为输入信号向量，M为滤波器阶数；h(n)=[h0(n),h1(n),…,hM-1(n)]T为M阶滤波器系数；v(n)为独立于x(n)的系统噪声，并且假设滤波器结构与未知系统结构相同。相应的先验估计误差定义为

(2)

(3)

(4)

式中：μ(n)为LMS算法步长。假定式(1)中v(n)=0(即假定没有噪声存在)，可以得到

d(n)=xT(n)h(n)

(5)

结合式(3)~式(5)并令ε(n)=0，得到NLMS的步长为

μ(n)=[xT(n)x(n)]-1

(6)

由此得到标准NLMS的系数更新公式

(7)

式中：δ为一个非常小的正数，目的是防止出现xT(n)x(n)=0而出现的病态情况。式(7)的推导是在v(n)=0的假设下得到的，但是在实际中一般情况下v(n)≠0，此时，NLMS算法系数更新公式变为[7-10]

(8)

式中：γ(n)为归一化步长因子，0≤γ(n)≤1。

2.2算法描述

本文算法在文献[7]的框架下对步长因子γ(n)改变方案进行改进，具体改进方法如下式

(9)

式中：α为一个非常接近于1的常数，经验值为0.999；f(e(n))=b(1-exp(-a|e(n)e(n-1)|))为迭代误差e(n)对步长因子γ(n)的贡献量。(1-α)f(e(n))为当系统变量ζ(n)小于系统变量阈值ζth时，n时刻步长因子γ(n)在前一时刻γ(n-1)的基础上的调整量。ζ(n)为系统变量，定义式为[7-10]

(10)

ζ(n)能够根据输出数据d(n)和迭代误差e(n)表征迭代系数的状态，并为分段变步长方案提供分段依据。式(10)中各个变量的计算方法如下[7-11]

(11)

(12)

(13)

2.3算法分析

在此部分将对本文的NLMS算法进行可行性分析。可行性分析采用对比的方式，即与已经证明可行的NLMS(文献[7])进行对比，从而分析本文算法的可行性。

因为本文NLMS算法是在文献[7]的框架下进行的改进，所以这里选择文献[7]进行对比和分析。文献[7]所采用的步长因子γ(n)改变方案为

(14)

按照式(9)可以将文献[7]理解为如下形式

(15)

(16)

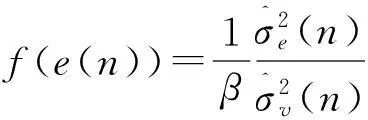
根据文献[7-10]，算法可行需要满足的条件是： 迭代初期，步长因子γ(n)应该较大(最大不能超过1)；随着迭代次数增加，γ(n)随着e(n)逐渐减小；达到最优收敛性能时，γ(n)应非常接近于0。经过大量的实验和尝试，找到满足这样要求的方案，如式(9)，为了便于观察和分析，我们将式(9)中f(e(n))与e(n)的关系用图形展示出来(b=10，a=0.6)。具体情况如图3所示。

图3　叠加量随迭代误差变化图

从图3可以看出：当e(n)>7时，f(e(n))为1，此时以最大的步长因子加快收敛速度；随着迭代次数的增加，e(n)逐渐减小，f(e(n))也逐渐减小，从而兼顾收敛速度和稳态误差两对矛盾；当e(n)逐渐接近于0时，也就是接近于最优收敛性能时，f(e(n))非常接近于0，能够有效减小稳态误差。

通过以上分析可以得出：本文提出的变步长方案虽然在思路上与文献[7]相差很大，但是在核心思想是相通的，能够满足文献[7]的可行性要求。因此，本文方案在理论上是可行的。

3仿真结果及分析

此部分在时不变环境下基于系统辨识收发隔离模型的基础上，将本文提出的基于先验误差的变步长NLMS算法应用到收发隔离中。首先，提出收发隔离性能的量化衡量指标；然后，通过仿真比较和分析本文隔离方案与文献[5]所提出隔离方案的隔离性能。

3.1隔离性能衡量指标

1)能量比

经过干扰对消后的敌雷达信号与真实雷达信号的差值的能量占真实敌方雷达信号能量的比值，简称能量比。其定义式为

(17)

式中：x(k)为真实敌方雷达信号；x′(k)为经过干扰对消后的敌方雷达信号。能量比从能量角度反映了经过干扰对消措施后的敌雷达信号与真实雷达信号的接近程度，是衡量隔离措施的前提。因为如果经过对消措施后的敌雷达信号与真实的敌方雷达信号差距很大的话，证明隔离措施对敌雷达信号产生了很大的影响，而这违背了收发隔离的初衷。

2)隔离后信干比

隔离后信干比决定了侦察接收机能否正常接收敌方雷达信号，隔离后信干比如果大于接收机正常工作所需的信噪比，则证明隔离方案不需要其他隔离措施也是有效的，否则说明还需要附加其他的隔离措施才能保证接收机的正常工作。

3)隔离前后信干比改善量

将隔离后的信干比与隔离前的信干比做差值，就得到了信干比改善量，用于量化对比不同隔离措施的隔离效果。

3.2隔离性能比较

为了便于对比效果，本文仿真参数的设置同文献[5]条件相同。假定敌方雷达信号为单频调制连续正弦波信号，频率为2.5 kHz，敌方雷达信号的信噪比为40 dB，施放的干扰为噪声调幅信号，载频为2.5 kHz，接收机接收频率范围为[2 450，2 550]。用来探测系统的探测信号设置为高斯白噪声，参考信号的信噪比为30 dB，采样频率为10 kHz，采样时间T为3.6 s。假设耦合环境传递函数为H(z)=0.8z-1+0.5z-3+0.1z-5，自适应滤波器阶数设置为8阶。本文变步长NLMS算法的参数设置为：α=0.999 3，δ=0.000 1，a=0.6，b=10，ζth=0.35，仿真结果在100次独立实验下得出。

实验1：系统辨识情况比较

如图4所示，画出了本文自适应算法与文献[5]所采用的自适应算法对耦合环境的传递函数的辨识情况，传递函数为H(z)=0.8z-1+0.5z-3+0.1z-5，文献[5]经过3.6 s的采样后辨识结果是(图5中的实心点)：(0.7581，-0.0039，0.4722，-0.0031，0.0966，-0.001 1，-0.001 1，-0.001 2)，而本文的自适应算法经过同样采样时间后辨识的结果为(图5中的叉)：(0.80005，0.000038，0.50001，-0.000042， 0.1002，-0.000 091，0.000 221，-0.000 22)。通过两组数据和图形可以看出：本文NLMS算法的辨识精度优于文献[5]所采用的自适应算法。两种算法辨识精度的差距可以通过局部放大图清楚地观察到，考虑到干扰信号通常功率很大，因此，很小的差距经过多阶滤波器后，差距就会变得很大，从而隔离性能相差很多，这在下面的仿真中得到了证明。

图4　两种算法辨识性能对比

实验2：隔离性能比较

为了全面衡量隔离效果，从残余干扰信号与真实敌方雷达信号的能量比、经过干扰对消后的敌方雷达信号与真实雷达信号的时频域对比情况、隔离前后干扰信号的时域对比情况、隔离前后信干比情况等角度进行分析，具体情况如图5所示。

图5　残余干扰信号能量对比分析

由图5可以清楚地看出：经过文献[5]的隔离措施后，残余的干扰信号能量(经过干扰对消后的敌方雷达信号与真实雷达信号的差值)较大，残余干扰信号的能量是真实雷达信号能量的110倍左右(图5中的实心点)；而经过本文的隔离措施后，残余干扰信号的能量占真实雷达信号能量的比例大约为8.04%(图5中的空心圈)，这样小的残余干扰信号不会对真实雷达信号产生本质的改变。

由图6、图7可知：对消前耦合到接收端的干扰信号的幅度在±5 V之间，经过文献[5]的隔离措施后，干扰信号的幅度在(3×10-2)V之间，而经过本文隔离措施后，干扰信号的幅度在±(2.5×10-4)V之间，将干扰信号的幅度在文献[5]的基础上削减了2个数量级。

图6　对消前干扰信号

图7　两种隔离方案隔离后干扰信号对比

为了便于观察，时域只取0.01 s的信号进行观察，图8a)、b)为经过文献[5]的隔离措施后，敌方雷达信号与真实敌方雷达信号时频域对比情况。图8a)、b)中虚线表示真实的敌方雷达信号，实线表示经过隔离措施后叠加了残余干扰信号的敌方雷达信号。可以清楚地看出：经过隔离后的敌方雷达信号与真实雷达信号差距较大，尤其是在幅度上，这在频域对比图上也能得到证明，而收发隔离的理想目标是敌方雷达信号保持不变，即无论是从时域还是频域角度两个信号都尽可能地接近。

图8　文献[5]隔离后的雷达信号与真实雷达信号时频对比

图9a)、b)展示的是经过本文隔离措施后，敌方雷达信号与真实雷达信号时频域对比情况。可以看出：无论是从时域还是频域进行对比，两种信号都非常的接近，尤其是从频域放大图可以看出，经过放大后的两信号的频域几乎重合，说明本文隔离方案几乎未对真实的雷达信号产生改变，对消掉大功率干扰的同时保持了敌方雷达信号的本来性质。

图9　本文隔离后的雷达信号与真实雷达信号时频对比

通过图5、图9可以看出：经过本文隔离方案后的敌方雷达信号保留了原来的性质，没有发生本质的改变，这是隔离方案可行的前提；由图6、图7可以看出：本文隔离方案能够将耦合的干扰信号在文献[5]的基础上削减2个数量级，说明本文隔离措施是有效的。

由图10、图11可以看出：隔离前信噪比大约为-45 dB，经过本文隔离措施后，将信干比提高至少50 dB，使得隔离后的信干比在5 dB以上，而文献[5]隔离后信干比提高约28 dB，本文方案在文献[5]的基础上，将信干比又提高约22 dB。实际工程中本文隔离措施如果配合其他的隔离措施，如空间隔离提高约6 dB、隔离板增加约20 dB，将这些措施综合应用是可以满足工程需求的。

图10　本文与文献[5]信干比改善量对比

图11　本文隔离前后信干比情况

4结束语

本文针对固定步长的NLMS算法应用在基于自适应系统辨识的收发隔离中隔离性能不理想的问题，提出一种基于先验误差的变步长NLMS算法。该算法依据相邻时刻先验误差的相关系数调整步长因子，这样的步长因子改变能够在算法收敛过程中削弱噪声的影响，提高了算法辨识精度。将此变步长NLMS算法应用在收发隔离中，提高了隔离性能。仿真结果表明：(1)经过本文隔离方案后的残余干扰信号能量与真实敌方雷达信号能量的比值为8.04%，隔离措施未对真实雷达信号产生本质影响，在削弱耦合干扰信号的同时保持了其原来的性质，本文方案是可行的；(2)信干比改善量在文献[5]的基础上提高约20 dB，隔离方案是有效的；(3) 本文方案结合其他隔离措施使得隔离后的信干比能够满足工程要求，具有工程实用性；(4)本文算法步长因子每次迭代更新需要进行对数运算，因此，计算复杂度较高，是下一步工作的重点。

参 考 文 献

[1]刘国岁，孙光民，顾红. 连续波雷达及其信号处理技术[J]. 现代雷达，1995，17(6)：35-36.

Liu Guosui，Sun Guangmin，Gu Hong. CW radar and its signal processing technique[J]. Modern Radar，1995，17(6)：35-36.

[2]谢旻睿. 有源干扰的收发隔离技术研究[D]. 西安: 西安电子科技大学，2012.

Xie Minrui. Research on transmitter-receiver isolation technology of active jamming[D]. Xi′an：Xidian University，2012.

[3]饶睿楠. 自适应对消的收发隔离技术[D]. 西安: 西安电子科技大学，2006.

Rao Ruinan. Adaptive cancellation technique for transmitter-receiver isolation[D]. Xi′an：Xidian University，2006.

[4]桑乃建，汪学刚. 一种基于分数延时滤波器的自适应对消技术的研究[J]. 雷达与对抗，2011，31(4)：29-33.

Sang Naijian，Wang Xuegang. A research on adaptive cancellation technique based on fractional delay filter[J]. Radar & ECM，2011，31(4)：29-33.

[5]张凯，王建业. 基于自适应系统辨识的收发隔离技术研究[J]. 现代防御技术，2010，38(1)：78-80.

Zhang Kai，Wang Jianye. Research on transmitter receiver isolation technique based on adaptive system identification[J]. Modern Defence Technology，2010，38(1)：78-80.

[6]Kay S M. 统计信号处理基础[M]. 罗鹏飞,译. 北京: 电子工业出版社，2012.

Kay S M. Fundamentals of statistical signal processing[M]. Luo Pengfei,translate. Beijing：Publishing House of Electronics Industry，2012.

[7]Huang H C，Lee J H. A new variable step-size NLMS algorithm and its performance analysis[J]. IEEE Transactions on Signal Processing，2012，60(4)：2055-2056.

[8]Benesty J，Rey H. A nonparametric VSS NLMS algorithm[J]. IEEE Transactions on Signal Processing，2006，13(10)：581-584.

[9]Paleologu C，Benesty J. A family of variable step-size NLMS algorithms for echo cancellation[J] . IEEE Transactions on Signal Processing，2010，55(1)：49-58.

[10]Iqbal M A，Grant S L. Novel variable step size NLMS algorithm for echo cancellation[C]// IEEE International Conference on Acoustics, Speech, and Signal Processing. Las Vegas, NV: IEEE Press，2008： 241-244.

[11]Udrea R M，Paleologu C. Estimation of the noise power in the NPVSS-NLMS algorithm[J]. IEEE Transactions on Signal Processing，2010，50(2)：385-388.

邹纯烨男，1989年生，硕士研究生。研究方向为雷达信号处理。

张剑云男，1963年生，教授，博士生导师。研究方向为雷达信号处理、阵列信号处理、目标环境模拟等。

周青松男，1982年生，博士，讲师。研究方向为雷达信号处理、阵列信号处理、凸优化理论等。

黄中瑞男，1988年生，博士研究生。研究方向为雷达信号处理、凸优化与方向图综合等。

·信号/数据处理· DOI：10.16592/ j.cnki.1004-7859.2015.11.006

A Study on Transmitter-receiver Isolation

Based on Adaptive System Identification

ZOU Chunye，ZHANG Jianyun，ZHOU Qingsong，HUANG Zhongrui

(Radar Electronic Warfare Department 502 Teaching and Research Section,

Hefei Electronic Engineering Institute,Hefei 230037, China)

Abstract：Transmitter-receiver isolation is a inevitable problem for airborne jammer. Lower efficiency of jammer and even self-excitation might be caused by lower degree of transmitter-receiver isolation. Transmitter-receiver isolation is not satisfactory when the fixed step size normalized least mean square (NLMS) algorithm is implemented because of worse estimation accuracy. To solve this problem, a variable step-size NLMS algorithm based on prior estimation error is proposed in this paper. The correlation coefficient of the adjacent moment prior estimation error is employed in this NLMS algorithm to control the step size adaptively. The estimation accuracy as well as the isolation performance is improved by weakening the impact of syetem noise in this step size update scheme. The theory analysis and simulation results demonstrate that the performance of transmitter-receiver scheme based on the proposed variable step-size NLMS algorithm is better than schemes which are based on other least mean square algorithms.

Key words：transmitter-receiver isolation; adaptive system identification; prior estimation error; normalized least mean square algorithm

收稿日期：2015-07-22

修订日期：2015-09-22

通信作者：邹炖烨Email：chunye200ye@163.com

中图分类号：TN957

文献标志码：A

文章编号：1004-7859(2015)11-0016-06