基于模糊网络的机翼天线变形测量方法

封思远，保　宏，张旭东

(1. 西安电子科技大学 电子装备结构教育部重点实验室，　西安 710071)

(2. 南京电子技术研究所，　南京 210039)



基于模糊网络的机翼天线变形测量方法

封思远1，保宏1，张旭东2

(1. 西安电子科技大学 电子装备结构教育部重点实验室，西安 710071)

(2. 南京电子技术研究所，南京 210039)

摘要：高空长航时无人预警机的发展日益受到重视，而对其机翼长基线天线变形的实时高精度测量对保证天线性能具有重要意义。结合模糊自构架理论，提出了一种适于机翼变形实时测量的模糊网络法。首先，根据测得的机翼上各个位移测量点的形变位移量和相关应变点的应变量，自主构架网络来逼近二者之间的关系；然后，以空间三角桁架为对象进行仿真分析，并在静载作用下对铝制翼板模型进行变形测量实验。研究表明：模糊网络法具有较高的测量精度和较快的训练速率，为机翼变形测量提供了一种新的思路。

关键词：机翼长基线天线；模糊网络；自构架；变形测量

0引言

在现代信息化战争中，高空长航时无人预警机作为一种全天候的战场信息获取手段发挥着不可替代的作用[1]。这类飞机普遍采用轻质大展弦比柔性机翼，具有升阻比大、结构轻、柔性大等特点[2-3]，而此时机翼通常就是一部长基线天线。在气动载荷作用下，机翼会产生很大的弯曲和扭转变形[4-5]，使得天线无法满足自身型面要求，从而导致天线电性能急剧下降[6]。因此，机翼变形的实时高精度测量具有重要意义。

目前，机翼变形实时测量系统可以分为两大类：光电测量系统和非光电测量系统。光电测量系统使用成像的方式直接探知结构中目标点的位置[7-8]，变形重构算法相对简单，考虑到实际测量的环境，很难得到高精度的测量结果，并且成本高、质量重及安装困难等问题限制了其应用；非光电测量系统，多基于曲率或应变信息对变形进行重构，其中，如何由传感器信息推导出形变位移则是问题的关键。文献[9]利用模态重构法建立应变与结构变形之间的关系，但其不适用于结构大变形的重构，并且需要知道材料参数，通用性不强。

对此，本文提出一种适于机翼长基线天线变形实时测量的模糊网络法。该方法根据测得的应变量和形变位移量，能够自主构架网络来逼近二者之间的非线性关系。以空间三角桁架为对象进行仿真分析，并利用自行搭建的实验平台对铝制翼板模型在静载作用下进行变形测量实验，完成整个测量系统有效性的初步实验验证。

1变形测量系统结构

变形测量系统主要分为两个阶段：模糊网络自构架训练阶段和直接应用阶段。在自构架训练阶段里，针对各个位移测量点，模糊网络通过自构架算法，从零规则开始自主构架规则库来逼近该测量点的形变位移量与相关应变量之间的非线性关系。当逼近误差满足要求后，对当前各个位移测量点训练完成的规则库进行固化保存，而此时，所有位移测量点的规则库则构成了应变输入与形变位移输出之间的模糊网络，如图1所示；在直接应用阶段，输入应变测量系统测得的应变量，经过模糊网络计算，直接得出所要求的各个测量点的形变位移量输出，从而得到整个机翼长基线天线的整体变形，如图2所示。

图1　训练阶段框图

图2　应用阶段框图

在测量系统开始运行之前，需要把机翼长基线天线划分为若干个形变位移测量点，针对每个位移测量点，找到与其在多种载荷变形下紧密相关的若干个应变测量点。位移测量点的选取要尽可能反映出天线整体的变形情况，通常布置在形变位移较大处，并且根据变形情况，适当地分配密集程度。应变测量点的选取相对复杂，常用的布置方法有智能规划法[10]、模态动能法、有效独立法、特征向量乘积法等[11]，具体应用哪种方法应依据天线结构而定。在测量点确定后，分别利用位移测量系统和应变测量系统来测得在多种载荷情况下各个位移测量点的形变位移量和相关应变点的应变量。将不同载荷情况下的数据汇总，挑选部分形变位移量和应变量对应的数据作为模糊网络的训练样本。

2模糊网络法

模糊网络法基于T-S型模糊逻辑系统的普遍逼近特性[12]，能够以较高的精度逼近不同载荷情况下形变位移量和相关应变量之间的非线性关系。该算法采用三角隶属函数，能自主增加和删除隶属函数与规则，时刻保持系统的最简状态，并且针对所施加的不同载荷情况，进行统一训练，无需单独区分，同时，也无需了解对象的材料参数，通用性较强。模糊网络法的自构架训练阶段大致分为四个过程：增加隶属函数和规则；删除隶属函数和规则；自适应规则后件；固化规则库。

1)增加隶属函数和规则

根据以下两个准则[13]判断是否需要增加隶属函数：

(1)系统误差准则：以系统的均方根误差(RMS)来描述系统误差。若系统误差大于一个预先设定的误差阈值Er，则说明当前隶属函数分布不能很好地描述应变输入和位移输出之间的关系，需要增加隶属函数。

(2)ε完备性：针对每一个输入变量都至少存在一个隶属函数，其隶属度不小于一个设定值ε， 一般取0.5。找出所有输入变量对应的最大隶属度，若最大隶属度中的最小值小于ε，则需要增加隶属函数。

在增加隶属函数之前，针对每个应变输入，需要判断当前应变值是否与已有的隶属函数中心点重合，若重合，则只生成规则，而不再增加新的隶属函数。当一个新隶属函数增加时，则以当前该输入应变的值为中心点，相邻隶属函数的中心点分别为左右端点。同时，相邻隶属函数的端点也要调整为新增隶属函数的中心，以保持一个连续的隶属函数分布。

在生成规则时，以当前各个应变输入中隶属度最大的隶属函数为规则前件，实际测得的形变位移量为规则后件，每次只生成一条规则。假设某位移点有N个相关应变输入x1,x2,…,xN，规则形式为

THENy=αi

(1)

(2)

式中：Nrules为模糊规则数；μi为第i条规则的激活度；其中

从小额诉讼程序具体适用情形看，在韩国的民事案件中，标的额较小的案件所占比率为70.03%，如根据其2011年司法年鉴，2011年一审的民事案件共计985333件，其中和解案件为55374件，独立审判的案件 239920件，小额案件 690239件。［10］可见，韩国小额案件程序不是仅仅针对一般意义上的小额案件，而是民事诉讼通常程序外的所有案件。

x(k)=(x1(k),x2(k),…,xN(k))

2)删除隶属函数和规则

如果一个自构架模糊系统只能增加隶属函数和规则，那么随着训练数据不确定性的增加，规则数的增加则必然导致计算负担的增大和参数学习效率的降低。因此，有必要删除那些对系统作用可忽略不计的隶属函数和规则，保持系统的精简性。定义规则贡献率Ci为第i条规则的输出占系统总输出的比例，Si为规则的删除指标，如下式[15]

(3)

(4)

式中：yi=αiφi；Si′为前一步的Si值；τ是范围为(0，1)的衰减因子；β为更新阈值。Si初始化为1，如果Ci小于β，则Si衰减，否则Si保持不变。当Si衰减到低于删除阈值Ω时，则删除该条规则。

当删除部分规则后，一些隶属函数就不再起作用了，因此，把所有规则中都未涉及到的隶属函数予以删除。同时，调整相邻隶属函数的端点，使其保持连续的隶属函数分布。

3)自适应规则后件

规则后件的调整是基于系统当前估算的形变位移输出值和实测的形变位移量，对规则后件进行赏罚策略的调整。在当前k时刻，第i条规则后件调整的具体表达式为[16]

Δαi(k)=γμi(k-1)[r(k-1)-y(k)]

(5)

式中：μi(k-1)和r(k-1)分别为在k-1时刻第i条规则的激活度和实测的形变位移量；y(k)为当前k时刻系统估算的形变位移输出值；γ为常量，其大小直接影响到后件调整的快慢。

当模糊网络自构架完成，并且经过多次训练，精度满足指标要求后，则把当前各个位移测量点对应的规则库进行固化保存。在应用阶段中，输入与各个位移测量点相关的应变量，经过固化后的模糊网络快速计算，直接得出各个测量点符合精度要求的形变位移量输出，模糊网络法的流程图如图3所示。

3仿真与实验

3.1桁架模型仿真分析

以长度为30 m空间三角桁架为仿真对象，等长度分为100个桁架段。以桁架首端为固定端，考虑到此时的桁架是自然分段，并且由于三角形框的约束，导致在连接点的两边，应变存在着不连续的现象。因此，在连接点两边分别布置应变测量点，最后，总的应变测量点的数目为597个，其中，两个桁架段的应变测量点的分布情况如图4所示。以各个连接点作为位移测量点，总的位移测量点的数目为300个。在中间桁架段上的各个位移测量点，以相邻的两个应变测量点的应变量作为输入构成两应变输入单位移输出的规则库，而在尾端的三个位移测量点，则以相邻的一个应变测量点的应变量作为输入构成单应变输入单位移输出的规则库，从而构成整个桁架的模糊网络。

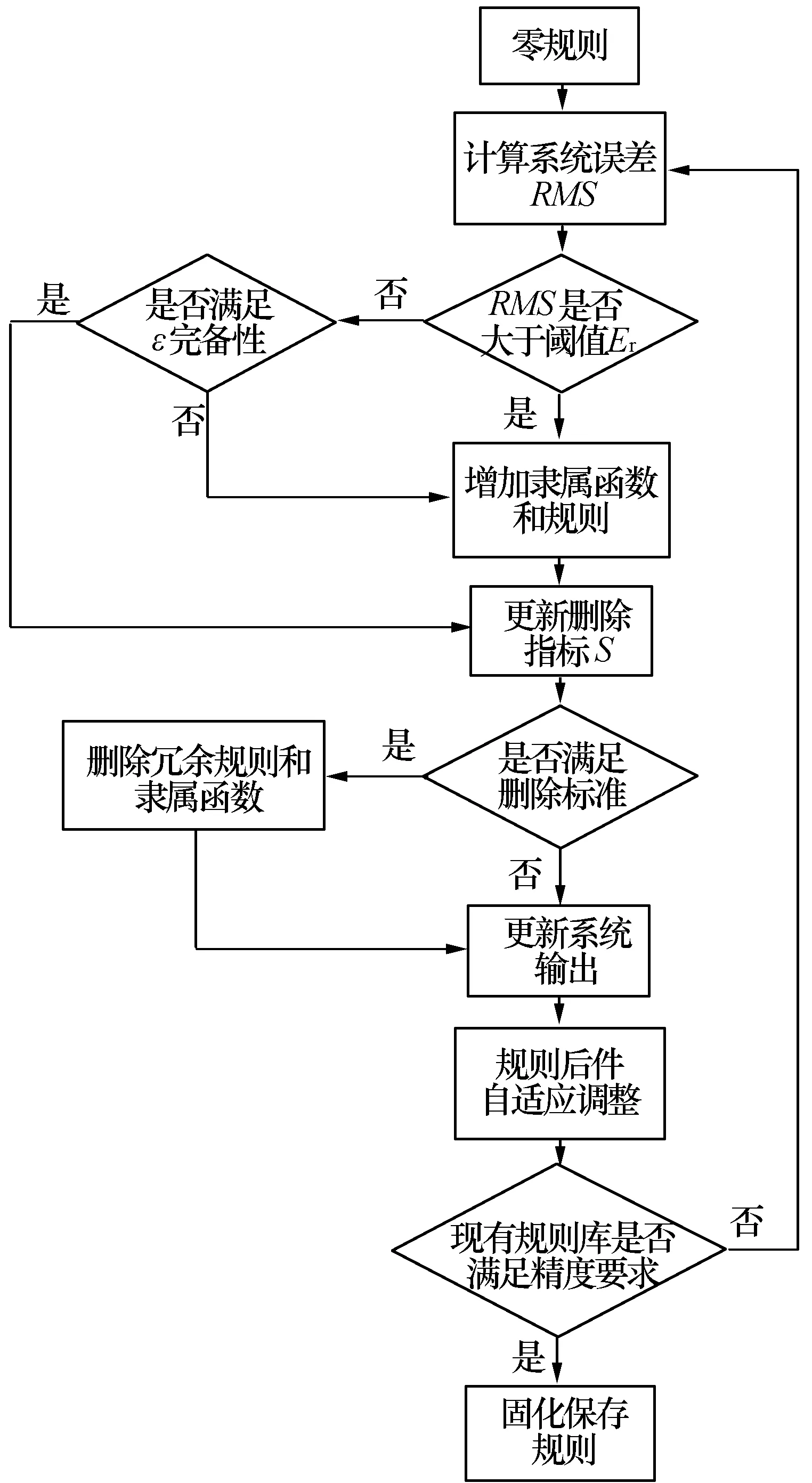
图3　模糊网络法流程图

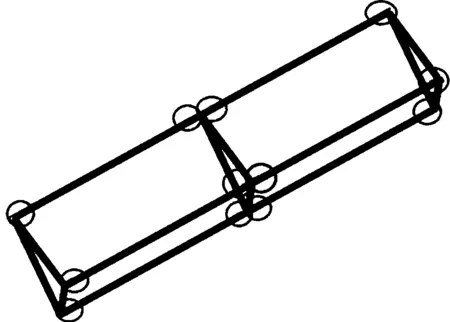
图4　应变测量点分布示意图

针对桁架300个位移测量点，分别均匀地以0.3 N等间隔的从-14.6 N到14.6 N施加纵向载荷力，并利用ANSYS软件分析得出各测量点对应的应变量和形变位移量，作为样本数据进行模糊网络自构架训练。当位移测量点的整体训练精度误差RMS<1 mm时，固化保存网络。利用固化后的网络，使整个桁架在一个均匀竖直向上且大小为10 N的载荷力作用下，对全部位移测量点进行形变位移量的估算测试，结果如图5、图6所示。

图5　桁架整体变形状态

图6　各位移测量点对应的形变位移估算误差

此时，位移测量点的整体形变位移估算误差RMS=0.048 2 mm。可以看出：模糊网络法能够以较理想的误差精度来逼近应变输入和相应形变位移输出二者之间的关系，验证了该方法理论上的可行性。

3.2翼板模型测量实验

为检验所提出的变形测量方法在实际中的有效性，设计翼板模型静态测量实验，测量翼板在末端单点集中载荷作用下竖直方向上的形变位移量。翼板模型的外形几何尺寸如图7所示，翼板厚度为5 mm，材料为6061-t6铝。

图7　翼板几何尺寸

实验过程中分别利用应变测量系统和位移测量系统来同时测量翼板测量点的应变量和形变位移量，整套实验系统如图8所示。应变测量系统由电阻式全桥应变片(BFH350-1.5EB-Q3)、信号放大器(BSFY-1)以及数据采集卡(阿尔泰USB2831)组成，位移测量系统由高精度动态三维光学测量仪(NDI Optrotrak Certus)及其配套软件组成。

图8　实验系统整体示意图

由于翼板末端的形变位移较大，因此，在翼板末端选取一个位移测量点，对其在竖直方向上的形变位移量进行测量。根据翼板模型的结构，利用智能规划法[10]来确定应变测量点的数量和位置，并从中选取两个距离位移测量点较近的应变测量点作为相关的应变输入进行测量。在翼板末端，逐次从0 kg~4.2 kg增加载荷，选其中7组不同载荷下的数据进行训练，并另选取3组不同载荷下的数据进行测试，其结果如表1、表2所示。由于上述应变测量系统直接测得的是电压量，需通过下式进行转换得到应变值。

(6)

式中：Uf为载荷作用下的输出电压；U0为零载荷时的输出电压；Am为信号放大器的放大倍数；Ue为应变传感器的激励电压；k为传感器的灵敏度系数。

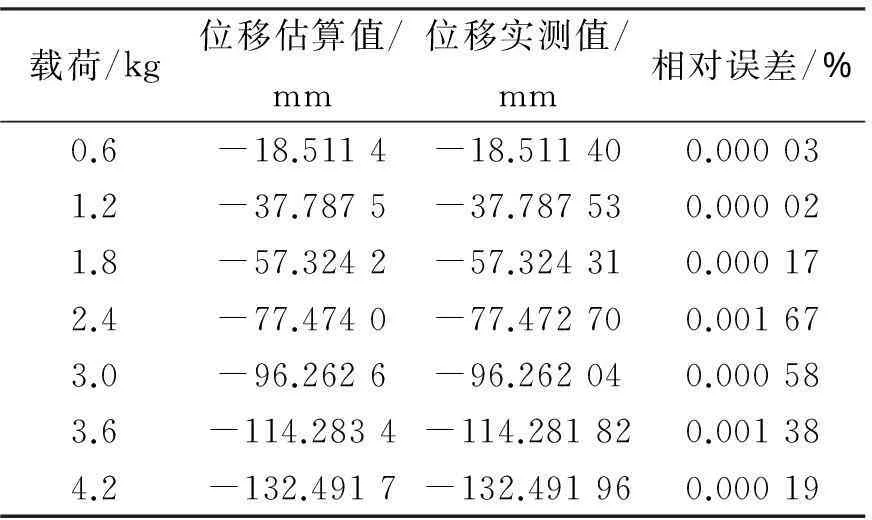
表1　模糊网络法的训练结果

表2　模糊网络法的测试结果

为直观地说明模糊网络的逼近情况，以施加的载荷(0 kg~4.2 kg)为横坐标，绘制对应的逼近曲线，如图9所示。可以看出：逼近曲线严格穿过参与训练的样本数据点，并与未参与训练的测试数据点较为接近。曲线整体变化相对平缓，没有出现剧烈的拐点，也间接表明了模糊网络法的稳健性。

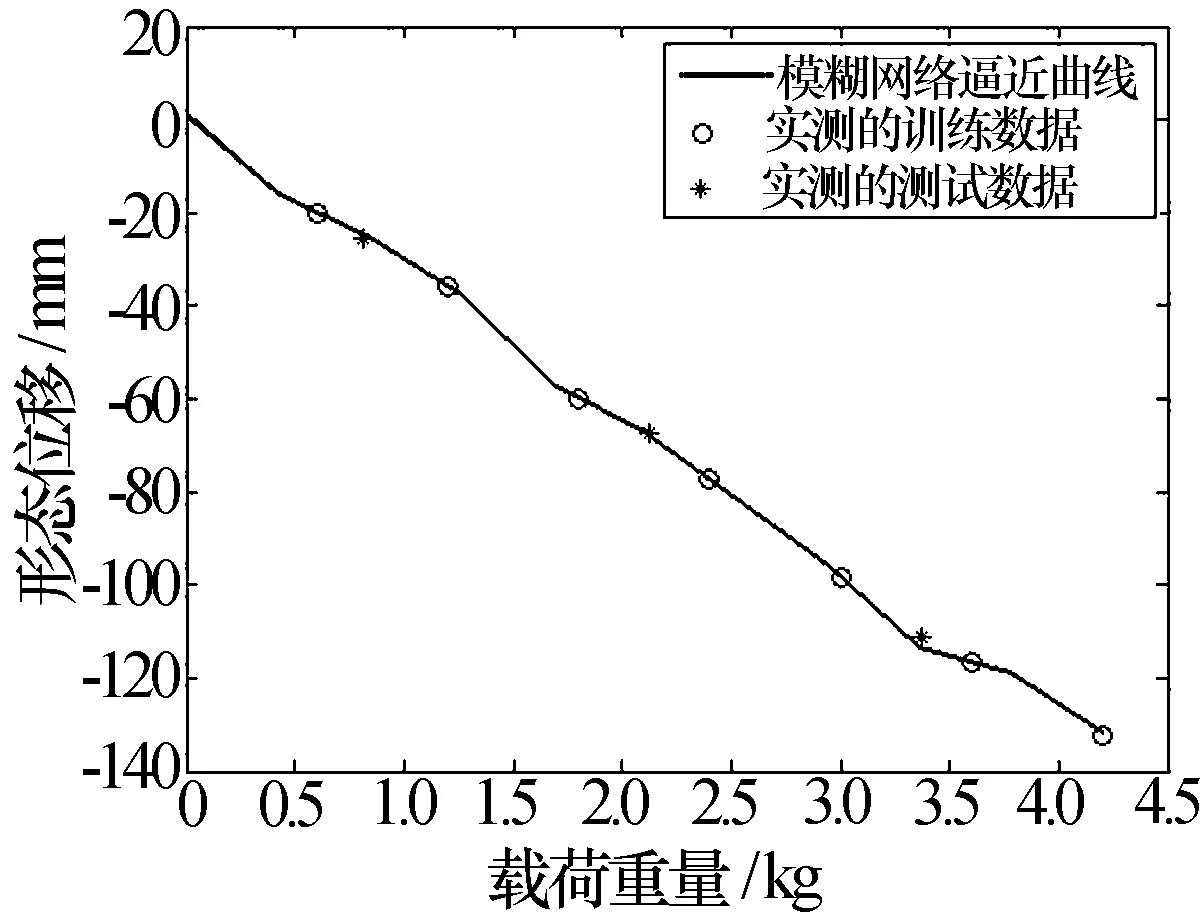
图9　模糊网络逼近曲线及实测数据点

由上述实验结果可知，随着位移测量点的形变位移量的增大，形变位移的估算误差有增大的趋势，但仍在一个较理想的范围内，说明建立的模糊网络能够较为准确地反映出结构变形的非线性规律，为进一步实现机翼长基线天线变形测量及外形重构提供了一定的理论及实验基础。但由于模糊网络是基于测量的应变量和相应的形变位移量进行自构架训练，因此，测量点的布置以及相关应变点的选取会对测试结果的精度影响较大。

4结束语

本文提出了一种适于机翼长基线天线变形实时测量的模糊网络法，该方法能较好的反映出相关应变量输入和相应形变位移量输出二者之间的关系，具有训练速率快、测量精度高、通用性强等特点。但由于高空长航时无人机飞行环境复杂，如何进一步提高测量系统的抗干扰能力以及合理地选取及布置位移测量点和相关应变测量点则是下一步研究的重点。

参 考 文 献

[1]陈国海. 下一代预警机雷达技术[J]. 现代雷达, 2010, 32(3): 1-4.

Chen Guohai. Technologies for next generation airborne early warning radar[J]. Modern Radar, 2010, 32(3):1-4.

[2]谢长川, 吴志刚, 杨超. 大展弦比柔性机翼的气动弹性分析[J]. 北京航空航天大学学报, 2003, 29(12): 1087-1090.

Xie Changchuan, Wu Zhigang, Yang Chao. Aeroelastic analysis of flexible large aspect ratio wing[J]. JournaI of Beijing University of Aeronautics and Astronautics, 2003, 29(12): 1087-1090.

[3]马铁林, 马东立, 张华. 大展弦比柔性机翼气动特性分析[J]. 北京航空航天大学学报, 2007, 33(7):781-784.

Ma Tielin，Ma Dongli，Zhang Hua. Aerodynamic characteristic analysis of high-aspect ratio elastic wing[J]. JournaI of Beijing University of Aeronautics and Astronautics, 2007, 33(7): 781-784.

[4]杨国伟, 郑冠男. 基于静气动弹性效应的飞机型架外形修正方法研究[J]. 航空工程进展, 2012, 2(2):143-150.

Yang Guowei, Zheng Guannan. Aircraft jig shape correction method based on static aeroelastic analyses[J]. Advances in Aeronautical Science and Engineering, 2012, 2(2): 143-150.

[5]Armen D, Sami F M, Jessica A, et al. Strain-based deformation shape estimation algorithm for control and monitoring applications[J]. AIAA Journal, 2013, 51(9): 2231-2240.

[6]Emily J A, Jie B Y, Richard D H, et al. Identifying and compensating for phase center errors in wing-mounted phased arrays for ice sheet sounding[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(6): 3416-3421.

[7]Jonathan B C, Donny P W, Jaynath N K. Shape estimation of deforming structures[C]// 42nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamic, and Materials Conference and Exhibit. Seattle, Washington, USA:AIAA, 2001: 1-11.

[8]周永兴. 飞行试验机翼变形测量的一种方法[J]. 测控技术, 2013, 32(4):15-19.

Zhou Yongxing. One technology of the aircraft wing deformation measurement in flight-test[J]. Measurement and Control Technology, 2013, 32(4):15-19.

[9]Philip B B, Eric H, Ralph E G. Strucutural shape identification from experimental strains using a modal transformation technique[C]// 42th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamic, and Materials Confere. Norfolk Virginia, USA: AIAA, 2003:1 -18.

[10]Li D S, Li H N, Fritzen C P. Load dependent sensor placement method: theory and experimental validation[J]. Mechanical Systems and Signal Processing, 2012, 31: 217-227.

[11]李东升, 张莹, 任亮, 等. 结构健康监测中的传感器布置方法及评价准则[J]. 力学进展, 2011, 41(1): 39-50.

Li Dongsheng, Zhang Ying, Ren Liang, et al. Sensor deployment for structural health monitoring and their evaluation[J]. Advances in Mechanics, 2011, 41(1):39-50.

[12]Castro J L. Fuzzy logic controllers are universal approximators[J]. IEEE Transactions on Systems, Man and Cybernetics, 1995, 25(4):629-635.

[13]张涛, 保宏, 杜敬利, 等. 非仿射非线性系统的自主构架模糊控制器[J]. 控制与决策, 2014, 29(8): 1532-1536.

Zhang Tao, Bao Hong, Du Jingli, et al. Self-structuring fuzzy controller for nonaffine nonlinear system[J]. Control and Decision, 2014, 29(8):1532-1536.

[14]Pomares H, Rojas I, Gonzalez J, et al. Structure identification in complete rule-based fuzzy systems[J]. IEEE Transactions on Fuzzy Systems, 2002, 10(3): 349-359.

[15]Chen P C. Fuzzy and neural network control schemes with automatic structuring process for nonlinear dynamic systems[D]. Taiwan:National Chiao Tung University, 2008.

[16]谢朝杰. 隶属度函数自调整模糊控制器的研究[D]. 西安: 西安电子科技大学, 2014.

Xie Chaojie. Study of membership function self-adjusting fuzzy controller[D]. Xi′an: Xidian University, 2014.

封思远男，1992年生，硕士研究生。研究方向为模糊控制及模糊系统辨识。

保宏男，1971年生，教授，博士生导师。研究方向为柔性天线阵面保型与变形测量、非线性控制、电子装备主被动控制。

张旭东男，1983年生，博士，高级工程师。研究方向为机载轻型相控阵雷达天线结构设计。

·收/发技术· DOI：10.16592/ j.cnki.1004-7859.2015.11.016

·天馈伺系统· DOI：10.16592/ j.cnki.1004-7859.2015.011.014

An Airfoil Antenna Deformation Measurement Method

Based on Fuzzy Network

FENG Siyuan1，BAO Hong1，ZHANG Xudong2

(1. Ministy of Education Key Laboratory of Electronic Equipment Structure, Xidian University,Xi′an 710071, China)

(2. Nanjing Research Institute of Electronics Technology,Nanjing 210039, China)

Abstract：The development of high-altitude long-endurance unmanned airborne early warning aircraft is receiving more and more attention, and the high-precision measurement in real time deformation of the airfoil long baseline antenna has great significance to ensure the antenna performance. According to the theory of fuzzy self-structure, a fuzzy network which is suitable for the real-time measurement of the airfoil deformation is proposed. Firstly, it can build a network to approximate the relationship between the strain and displacement automatically. Then, a simulation analysis of the model of the triangular space truss and a deformation measurement experiment on the aluminum airfoil model under static load are presented. The results show that the fuzzy network method has a high measurement accuracy and a fast speed for training and provides a new way of thinking for the airfoil deformation measurements.

Key words：airfoil long baseline antenna；fuzzy network；self-structure；deformation measurement

收稿日期：2015-07-28

修订日期：2015-09-25

通信作者：保宏Email：Hbao@xidian.edu.cn

基金项目：国家自然基金重大计划(51490660);中国电科集团创新基金(2014)

中图分类号：TN82

文献标志码：A

文章编号：1004-7859(2015)11-0059-05