基于拉格朗日乘子法的Delta并联机器人简化刚体动力学建模方法

王　刚，刘延杰，吴明月，韩海军

(哈尔滨工业大学机器人技术及系统国家重点实验室，黑龙江 哈尔滨 150001)

A Simplified Rigid Body Dynamic Modelling Method of Delta Robot Based

on Lagrangian Multiplier Method

WANG Gang，LIU Yanjie，WU Mingyue，HAN Haijun

(State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150001,China)

基于拉格朗日乘子法的Delta并联机器人简化刚体动力学建模方法

王刚，刘延杰，吴明月，韩海军

(哈尔滨工业大学机器人技术及系统国家重点实验室，黑龙江 哈尔滨 150001)

A Simplified Rigid Body Dynamic Modelling Method of Delta Robot Based

on Lagrangian Multiplier Method

WANG Gang，LIU Yanjie，WU Mingyue，HAN Haijun

(State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150001,China)

摘要：针对广泛应用于高速抓放操作的Delta并联机器人，提出了一种基于拉格朗日乘子法的刚体动力学建模方法，并利用约束方程的全微分求解出了动力学模型的显示表达式。建立了机器人的逆运动学以及刚体动力学模型，考虑机器人从动臂臂杆为轻质碳纤维杆，两端为较重的金属附件的特点，建立了简化刚体动力学模型。并针对机器人常用的高速抓放轨迹进行仿真，将简化前后的2种动力学模型与ADAMS仿真结果进行对比。

关键词：并联机器人；拉格朗日乘子法；简化刚体动力学模型；逆运动学模型

中图分类号：TP241

文献标识码：A

文章编号：1001-2257(2015)07-0068-05

收稿日期：2015-04-02

基金项目：国家高技术研究发展计划(863)资助项目(2013AA040901)；黑龙江省科研机构创新能力提升专项计划项目(YC13D004)

作者简介：王刚(1991-)，男，河北保定人，硕士研究生，研究方向为机器人结构优化设计与运动控制；刘延杰(1975-)，男，黑龙江哈尔滨人，博士研究生导师，教授，研究方向为机器人技术及系统；吴明月(1982-)，男，黑龙江哈尔滨人，博士研究生，研究方向为机器人结构优化设计以及振动抑制方法；韩海军(1985-)，男，黑龙江哈尔滨人，博士研究生，研究方向为机器人传感技术与运动控制。

Abstract：Targeting a Delta parallel robot which is widely used for high speed pick-and-place operation, a novel approximation for simplified rigid body dynamic model based on Lagrangian multiplier method is established. Both of the inverse kinematic and rigid dynamic model are developed, and the dynamic model is simplified considering the actual situation of the robot. Comparing the calculation results of the dynamic model before and after the simplification with the simulation results show that the simplified rigid model can not only reduce the amount of calculation but also improve the accuracy of it.

Key words：parallel robot; Lagrangian multiplier method; simplified rigid body dynamic model; inverse kinematic model

0引言

Delta并联机构是一类由3个转动副分别驱动3个平行四边形运动支链，具有3个平动自由度的并联机构[1-3]。伴随着Delta并联机器人在高速分拣、装配、包装等领域的广泛应用，其研究重点已经从早期的正逆运动学求解、工作空间分析等基本问题逐渐集中于动力学建模上来，它是对并联机器人实施基于动力学模型控制的基础[4]。针对Delta机构，目前已有不少学者对其进行动力学研究，其中大多数人采用虚功原理法以及牛顿欧拉法[5-6]，利用数值方法进行求解，求解精度受到迭代次数的限制，而且没有得到力矩的显示表达式。并且在对机器人进行动力学建模时，都是针对Delta机构进行计算，没有考虑到Delta机器人的实际情况。因此，其求解精度不高。

针对上述2个问题，提出了一种基于拉格朗日乘子法，结合方程组中各变量的物理含义，利用约束方程的全微分求解动力学模型的显示的表达式的方法，并且根据Delta机器人的实际情况，对机器人模型进行了合理的简化，建立了动力学模型。

1运动学模型

1.1　机器人结构

Delta并联机器人为少自由度并联机器人，其结构如图1所示。由定平台、动平台以及由主动臂和从动臂组成的3条运动支链组成。主动臂驱动端与减速机输出法兰连接，另一端通过2个球铰分别与2根从动臂以及动平台构成平行四边形机构，两从动臂依靠拉簧与主动臂以及动平台装配在一起，机构本身具有3个平动自由度。在实际应用中，常需要增加第4个旋转自由度，因此加入第4轴。

图1　Delta并联机器人三维模型

由于引入的第4轴不会对运动学造成影响，因此在运动学建模过程中，将其省略；因并联机构每条支链中的两支从动臂构成平行四边形机构，其运动完全相同，可以简化为一支；因主动臂驱动轴、从动臂与主动臂转轴、从动臂与动平台转轴相互平行,即na||nB||nC。所以可以将主动臂l1i以及从动臂l2i向定平台中心o平移r，平移后从动臂交于一点P，动平台与静平台半径差为e=R-r，如图2所示。

图2　单个支链坐标系结构

1.2　系统运动学模型

在参考系o-x0y0z0下，P点的位置矢量oP可以表示为：

oP=oAi+ABi+BPi

(1)

只需要分别求解出oAi、ABi、BPi关于关节角θ的表达式即可。令

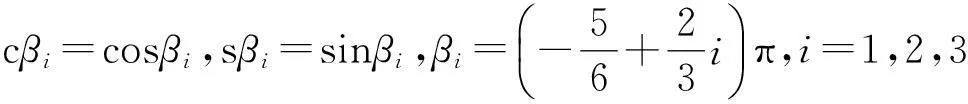
oAi=e·0Ri·ex

(2)

ex为x方向的单位向量，即ex=[100]T。沿主动臂方向的矢量AiBi可表示为：

AiBi=0Ri·iRAi·ex

(3)

其中，θi为驱动关节转角，规定向下为正方向；

BPi可由其余向量表示：

BPi=oP-oAi-ABi

(4)

又因为从动臂长度固定，所以

||BPi||=l2

(5)

可以得到并联机构的约束方程：

(6)

根据机构装配模式，可以求得Detla高速并联机器人的位置逆解模型为：

(7)

1.3　雅可比矩阵求解

系统的约束方程可以写为：

Гi(x，y，z，θ1，θ2，θ3)=(x-ecosβi-

l1cosβicosθi)2+(y-esinβi-l1sinβicosθi)2+

(z+l1sinθi)2-l22=0i=1，2，3

(8)

机构的约束方程只对形位进行约束，并且不显含时间t，为完整定常约束。系统为完整系统。式(8)对时间求导，整理可得：

(9)

A称为并联机构的正向雅可比矩阵，B称为机构的逆向雅可比矩阵。

机构的雅可比矩阵J为：

J=B-1·A

(10)

2动力学模型

2.1　拉格朗日乘子法建模

Delta并联机构有3个自由度，理论上需要3个广义坐标就能建立其动力学模型，但是由于delta机构的运动学比较复杂，如果只用(θ1，θ2，θ3)3个广义坐标来建立拉格朗日方程，那么得到的方程会极为复杂。因此，考虑利用拉格朗日乘子法建立动力学模型，引入3个多余坐标(x，y，z)，以及拉格朗日乘子(λ1，λ2，λ3)，则系统的广义坐标变为：

q=[x，y，z，θ1，θ2，θ3]T

系统的拉格朗日方程可写成如下形式：

(11)

n=6是广义坐标的数量，n=6是约束方程的数量，n-k=3是机构的自由度数。Гi是机构的第i个约束方程，λi是拉格朗日乘子。

前3个方程可以通过系统的约束获得：

(12)

Qj=[Q1，Q2，Q3]T为作用在机器人系统对应x，y，z自由度的非有势广义力，由于系统在x，y，z方向上不受外力作用，因此，方程中Qj=0。可以利用后3个方程求出作用在驱动关节上的驱动力：

(13)

Qj=[Q4，Q5，Q6]T即为所要求取的输入到机器人驱动关节上的3个驱动力矩Qj=[τ1，τ2，τ3]T。拉格朗日函数为系统的动能与势能之差：

L=K-V

(14)

因为Г(x，y，z，θ1，θ2，θ3)为系统的约束方程，而且θ1，θ2，θ3可由x，y，z表示，并根据自变量满足的条件，所以可以将约束方程写为：

(15)

由式(15)可得：

(16)

进而得到：

(17)

不难求出：

Q=[τ1，τ2，τ3]T=b+JT-1a

(18)

此结果将机器人各关节的驱动力矩表示为了显式表达式，便于对动力学模型的分析以及应用。

2.2　常规刚体动力学模型

一般地，在对Delta高速并联机器人进行动力学建模的过程中通常会进行2种假设[7-8]：将并联机器人的主动臂和从动臂等效为均质杆；将动平台等效为质点，第4旋转轴等效为动平台上的集中质量mx。

系统的总动能包括动平台动能与3条支链的动能，可以表示为如下形式：

(19)

其中，动平台与主动臂的动能求解较为简单：

(20)

从动臂的动能包括从动臂随某点的平动动能和从动臂绕这一点的转动动能。

(21)

从动臂随质心平移的速度为：

vbi=vBi+vCi

(22)

从动臂相对质心转动的角速度为：

(23)

将所有的运动矢量投影到支链坐标系oixiyizi中，如图3所示。

图3　从动臂空间刚体运动分解

从动臂与主动臂连接端Bi的速度为：

(24)

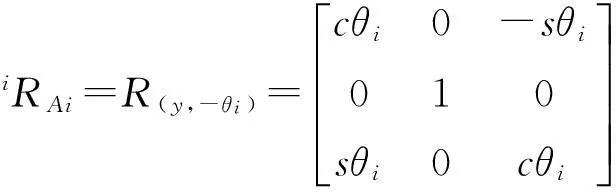
ez=[001]T

从动臂与动平台连接端Ci的速度为：

(25)

系统的所受的有势力为重力，因此系统的势能只包括动平台以及3条支链的重力势能。规定定平台所在平面为零势能面，则系统的势能可表示为：

(26)

Vp=mpgz

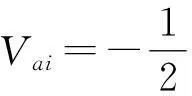
将所求得的机器人动能和势能代入式(14)得：

(27)

2.3　简化刚体动力学模型

结合Delta并联机器人的实际结构特点，考虑机器人从动臂的臂杆两端为铝合金的球铰接头，以及拉簧等零件，质量较重；而杆件主体为薄壁的碳纤维管，质量较轻。在对Delta并联机器人进行简化动力学建模的过程中进行3种假设：将并联机器人的主动臂等效为均质杆；将动平台等效为质点，第4旋转轴等效为动平台上的集中质量mx；将机器人从动臂等效为杆件两端的集中质量。

因此从动臂的空间刚体运动被简化为了质点的平面运动，从动臂动能简化为：

(28)

从而求得简化后的系统拉格朗日函数为：

(29)

动力学力矩表达式为：

Q=[τ1，τ2，τ3]T=b+JT-1a

(30)

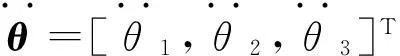
b为机器人各个驱动轴独立驱动各支链达到目标角加速度所需的力矩，a为机器人末端为达到目标加速度所需的力，即机器人3个驱动轴通过机器人结构模式作用到机器人末端的合力。因此JT-1a为机器人各支链间耦合产生的力矩，具体为各驱动轴作用到机器人末端的力，通过机器人机构模式耦合反馈到机器人驱动轴上所产生的等效力矩。

通过2种动力学模型的求解结果可知，简化动力学模型通过将从动臂等效为两集中质量，使得从动臂的空间刚体运动简化为了质点运动，消除了常规动力学模型中的速度耦合项，由于拉格朗日方程需要对各广义坐标的一阶导数求偏导，因此动力学模型的形式大大简化。

3对比分析

本文研制的Delta高速并联机器人如图1所示。工作空间为Φ 1 100mm×250mm的圆柱体。机器人动力学模型中的各物理量的数值见表 1。

表1Delta机器人物理参数定义

参数数值主动臂长度l1/m0.35从动臂长度l2/m0.80动静平台半径差e/m0.14机器人放置高度H/m0.60主动臂质量ma/kg0.85从动臂质量mb/kg0.24动平台质量mp/kg0.239旋转轴等效到动平台端质量mx/kg0.178主动臂等效转动惯量J1/(kg·m2)8.68×10-3驱动部件等效转动惯量Jm/(kg·m2)2.61×10-4主减速机减速比μ33

给定末端运动规律，设定最大运动加速度150 m/s2，末端负载为1 kg，图 4为常规动力学模型以及简化动力学模型力矩曲线与ADAMS仿真结果的对比。从图4可以看出，其驱动轴1和驱动轴3的力矩是相等的，3个轴中，轴2的峰值力矩最大。由图 4中常规动力学模型力矩曲线以及简化动力学模型力矩曲线分别与ADAMS仿真结果进行对比，可知2种动力学模型与仿真结果相差不大，力矩曲线的变化趋势相同，数值误差很小。

图4　力矩曲线对比

表2和表3分别为常规动力学模型的力矩曲线与ADAMS仿真结果的数值对比以及简化动力学模型与ADAMS仿真结果的数值对比。从表中的对比结果不难发现，简化动力学模型更符合机器人的实际情况，其计算所得的力矩曲线更接近仿真结果，其中轴1的最大峰值力矩误差由6.27%减小到2.07%，精度提升66.99%，最小峰值力矩误差由5.91%减小到1.54%，精度提升73.94%；轴2的最大峰值力矩误差由5.96%减小到1.88%，精度提升68.46%，最小峰值力矩误差由3.27%减小到0.66‰，精度提升97.98%。

表2常规动力学模型与仿真结果对比

参数ADAMS仿真/(N·m)常规模型/(N·m)幅值误差/%轴1最大力矩221.7207.8-6.27轴1最小力矩-214.8-202.1-5.91轴2最大力矩299.4289.6-3.27轴2最小力矩-244.8-230.2-5.96

表3简化动力学模型与仿真结果对比

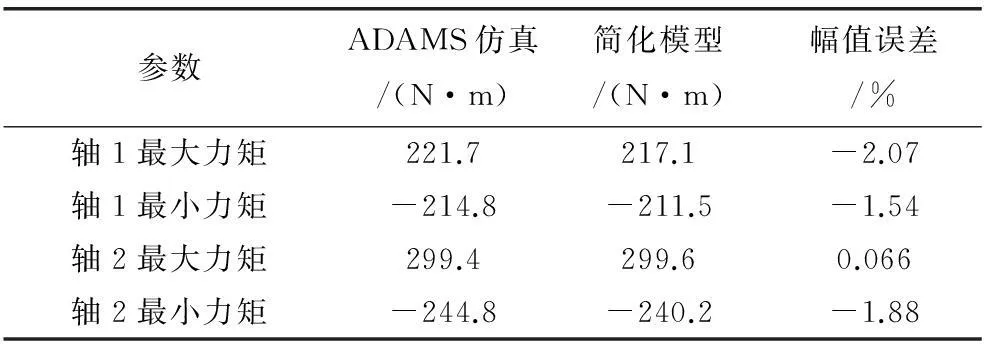
参数ADAMS仿真/(N·m)简化模型/(N·m)幅值误差/%轴1最大力矩221.7217.1-2.07轴1最小力矩-214.8-211.5-1.54轴2最大力矩299.4299.60.066轴2最小力矩-244.8-240.2-1.88

4结束语

利用拉格朗日乘子法建立了Delta并联机器人的动力学模型，并根据方程组中各变量的物理含义，利用约束方程的全微分将动力学模型化为显示的表达式。根据Delta机器人实际结构，考虑中间

旋转轴以及手臂附件的影响，对其动力学模型进行了合理的简化，并将其与常规动力学模型进行对比，在计算量方面，简化模型消除了速度耦合项，大大简化了计算。

参考文献：

[1]Pierrot F, Reynaud C, Fournier A. DELTA: a simple and efficient parallel robot[J]. Robotica. 1990, 8(2): 105-109.

[2]Clavel R. Device for the movement and positioning of an element in space[Z]. Google Patents, 1990.

[3]Merlet J. Parallel robots[M]. Springer Science & Business Media, 2006.

[4]冯李航，张为公，龚宗洋，等. Delta系列并联机器人研究进展与现状[J]. 机器人，2014，36(3): 375-384.

[5]Staicu S, Carp-Ciocardia D C. Dynamic analysis of Clavel's delta parallel robot[C]//IEEE International Conference on Robotics and Automation,2003：4116-4121.

[6]Khalil W, Ibrahim O. General solution for the dynamic modeling of parallel robots[J]. Journal of Intelligent and Robotic Systems,2007, 49(1): 19-37.

[7]Li Y, Xu Q. Dynamic analysis of a modified DELTA parallel robot for cardiopulmonary resuscitation[C]//IEEE/RSJ International Conference on Intelligtnt Robots and Systems,2005：233-238.

[8]从爽，尚伟伟. 并联机器人: 建模, 控制优化与应用[M]. 北京: 电子工业出版社, 2010.