基于惩罚回归样条的积分近似计算与应用

严恒普,　杨联强,　戴习民

(1.安徽大学数学科学学院,安徽合肥230601;　2.合肥工业大学数学学院,安徽合肥230009)



基于惩罚回归样条的积分近似计算与应用

严恒普1,杨联强1,戴习民2

(1.安徽大学数学科学学院,安徽合肥230601;2.合肥工业大学数学学院,安徽合肥230009)

[摘要]提出一种利用惩罚回归样条拟合被积函数f(x)，从而计算复杂积分f(x)dx的新方法.在仅知f(x)带随机扰动的离散数据点集的情况下，利用基于截断幂形式的样条基函数，通过惩罚样条回归，给出函数的多项式拟合结果，再根据该多项式形式便捷计算出积分.模拟和实际应用结果显示该方法计算简单快捷，并具有较好的准确度.

[关键词]惩罚样条； 积分计算； 回归

1引言

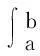
2惩罚回归样条与积分计算

2.1　惩罚样条回归

对于给定的离散数据点集(xi,yi)，i=1,2,…,n. 有多种方法可以发掘其内在的函数关系yi=f(xi)+εi，在以截断幂基样条函数为拟合工具情况下[6]，通常设

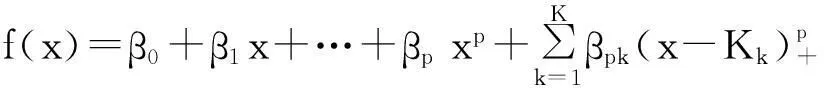
(1)

记

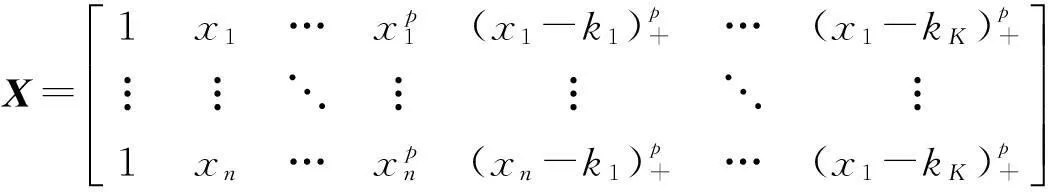
y=(y1,y2,…,yn)′，D=diag[0p+1,1m]，即D是由p+1个0和m个1构成的对角矩阵.模型(1)的拟合方法设为添加了惩罚项的广义最小二乘回归，目标函数为

‖y-Xβ‖2+λβ′Dβ,λ≥0，

(2)

其中λβ′Dβ称作惩罚项，其意义是控制拟合曲线对数据点的过度拟合现象，从而使得拟合曲线在拟合优度与曲线总体光滑性之间达到一个良好的平衡，λ称为惩罚参数.

令L=(y-Xβ)′(y-Xβ)+λβ′Dβ，化简后

L=y′y-2X′yβ+β′X′Xβ+λβ′Dβ，

(3)

(4)

(5)

惩罚参数λ的取值是使得如下定义的GCV(generalized cross-validation)得分取值最小的数值[6]，

2.2　积分计算

3模拟

本节给出两个被积函数已知的实例来说明上节方法的应用，并观察计算结果.

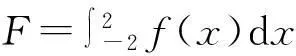
如图1a中所示，实曲线为原函数f(x)=sin2x+2e-16x2，虚线为拟合曲线，可以看出两条曲线几乎重合.图1b为筛选最优惩罚参数的结果图，在R软件中调用语句读出λ=31.5.

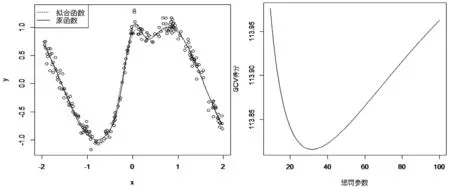
a.离散数据点、原函数、拟合函数　　　b. 惩罚参数取值　　　图1　例1中离散数据点集、原函数和拟合函数图像及惩罚参数取值图

(6)

a.离散数据点、原函数、拟合函数　　　　 b. 惩罚参数取值　　　图2　例2中离散数据点集、原函数和拟合函数图像及惩罚参数取值图

(7)

从(6)， (7)式相对误差来看，本文提出的积分估计方法还是比较合理的.

方法比较：我们还把本文提出的估计积分的方法与文献[1]，[2]中提出的方法进行了比较，首先可以借助Matlab的内置函数求出

基于本文惩罚样条回归估计下的积分值为F1=0.7029668，文献[1]中最佳积分值为F2=0.664468.相对误差分别为e1=0.09%，e2=5.1%;使用文献[2]中的方法计算出上述积的最佳值为F=0.634938，绝对误差e=9.5%.结果表明本文提出的估计积分的方法优于文献[1]，[2]中的方法.

4应用

基尼系数[8，9](Gini coefficient)是20世纪初意大利经济学家基尼，根据洛伦茨曲线所定义的判断收入分配公平程度的指标.基尼系数低于0.2表示收入过于公平；而0.4是社会分配不平均的警戒线，故基尼系数应保持在0.2～0.4之间，低于0.2社会动力不足；高于0.4，社会不安定.基尼系数的理论值等于绝对公平曲线与洛伦茨曲线所围面积与绝对公平曲线以下的面积之比.文章采用二次惩罚样条拟合的方法来拟合洛伦茨曲线.数据来源于《2011年安徽省统计年鉴》，以2010年安徽省农村居民人均年收入作为实证对象，计算出2010年安徽省农村居民的基尼系数，拟合结果如下：

图3　洛伦茨曲线的拟合

如图3，令绝对公平曲线与洛伦茨曲线所围面积为A，洛伦茨曲线以下的面积为B.则基尼系数理论值

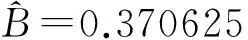
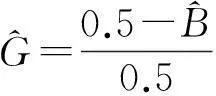
由此看来2010年安徽省农村居民人均年收入分配比较公平.

5总结

本文以基于截断幂基的惩罚回归样条为工具，给出了一种在已知函数带误差的离散数据点集的情形下求取该函数的积分的方法.该方法首先针对离散数据点集，通过惩罚样条回归拟合出函数的近似表达式，该近似表达式是以多项式形式给出的，通过该多项式表达式可以简洁的求出函数的积分近似值.该方法理论简单，计算快捷，模拟效果显示精确度较高，在实际应用中，具有较好的应用价值.

[参考文献]

[1]李平乐.工程设计中一类定积分的近似计算[J].湖南工业大学学报，2012，26(1):6-9.

[2]郑立飞，解小莉，王洁.关于定积分近似计算中矩形法的误差估计[J].高等数学研究，2011，14(001):5-6.

[3]刘清珺，陈婷，陈舜琮，等.正态分布积分近似计算公式及其在实验结果判定中的应用[J].现代测量与实验室管理，2009(3):21-23.

[4]杨少华.Monte Carlo方法在定积分近似计算中的应用[J].长春大学学报，2012，22(2): 185-187.

[5]Al-Nasser A D， Al-Talib M.The ranked sample-mean Monte Carlo method for unidimensional integral estimation [J].Asian Journal of Mathematics & Statistics，2010，3(1):130-138.

[6]Ruppert D，Wand M P，Carroll R J. Semiparametric regression [M].Cambridge University Press，2003.

[7]靳云汇，金赛男.高级计量经济学[M].北京：北京大学出版社，2007.

[8]张建华.一种简便易用的基尼系数计算方法[J].山西农业大学学报:社会科学版，2007，6(3):275-278.

[9]Al-Talib M M，Al-Nasser A D.Estimation of Gini-index from continuous distribution based on ranked set sampling[J].Electronic Journal of Applied Statistical Analysis，2008，1(1): 33-41.

Calculation of Integral Based on Penalized

Regression Spline and its Applications

YANHeng-pu1，YANGLian-qiang1，DAIXi-min2

(1.School of Mathematical Science，Anhui University, Hefei 230601，China;

2.School of Mathematics，Hefei University of Technology, Hefei 230009，China)

Abstract:This paper presents a new approach for calculating complex integral f(x)dx.When the discrete data points with errors of f(x) are given, the penalized regression splines are used to fit the function, and the fitted functions are expressed as polynomials. Then the integration can be calculated via the polynomials. Simulations and applications show that this method can be easily used and has good accuracy.

Key words:penalized splines; calculation of integration; regression

[基金项目]国家自然科学基金(11026076)

[收稿日期]2014-08-11

[中图分类号]O212.7

[文献标识码]C

[文章编号]1672-1454(2015)02-0056-05