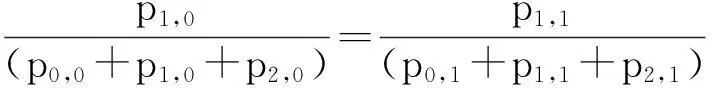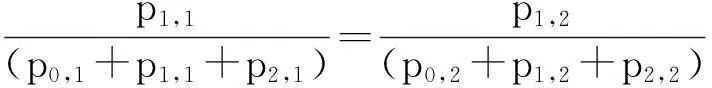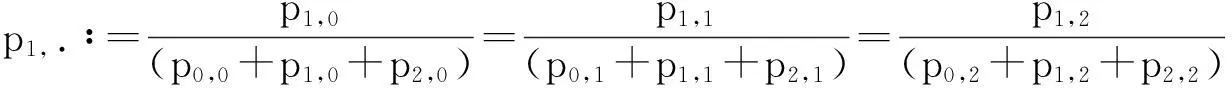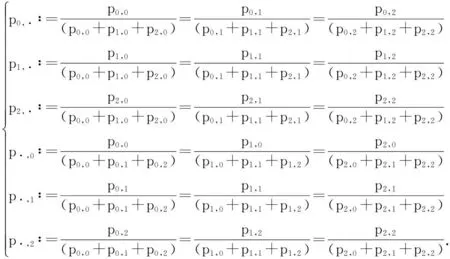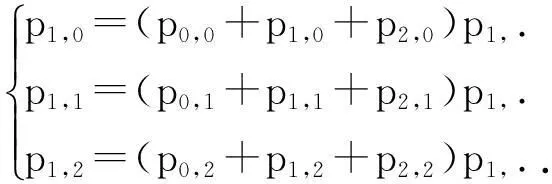二维连续型随机变量相互独立的一个充分条件
王 群, 彭小帆
(1.电子科技大学机械电子工程学院,成都611731; 2.电子科技大学数学科学学院,成都611731)
二维连续型随机变量相互独立的一个充分条件
王群1,彭小帆2
(1.电子科技大学机械电子工程学院,成都611731;2.电子科技大学数学科学学院,成都611731)
[摘要]提出了一个有关二维连续型随机变量相互独立的充分条件.该条件表明,如果二维连续型随机变量在任意概率值非0的矩形区域上被标准化后满足乘积的数学期望等于数学期望的乘积,则可推出它们是相互独立的.
[关键词]独立性; 二维连续型随机变量; 数学期望
1引言
随机变量之间的相互关系研究一直是一个重要的课题,而随机变量之间的相互独立性是描述随机变量之间相关关系最简单和最基础的性质.由独立性的定义我们知道,对于两个相互独立的随机变量,其乘积的期望等于期望的乘积,但其逆通常不正确[1].本文发现,如果一个二维连续型随机变量在任意概率值非0的矩形区域上被标准化后满足期望与乘积的运算可交换,则可推出它们是相互独立的.这里我们并没有依赖定义独立性时所需要的分布性质,而是直接考察随机变量在概率值非0的矩形区域上的数字特征.
2命题提出
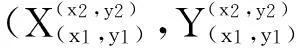
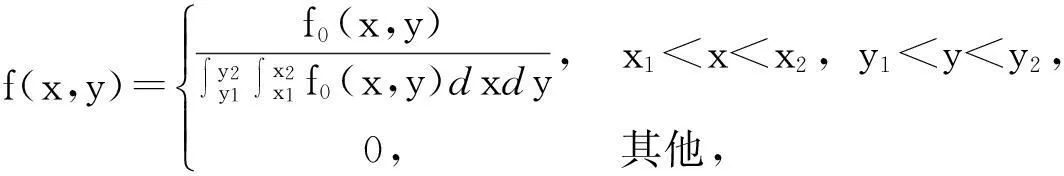
若有

(1)
则随机变量X与Y相互独立.
3证明
为便于讨论,我们将平面分成9个概率值皆不为0区域,如图1所示.
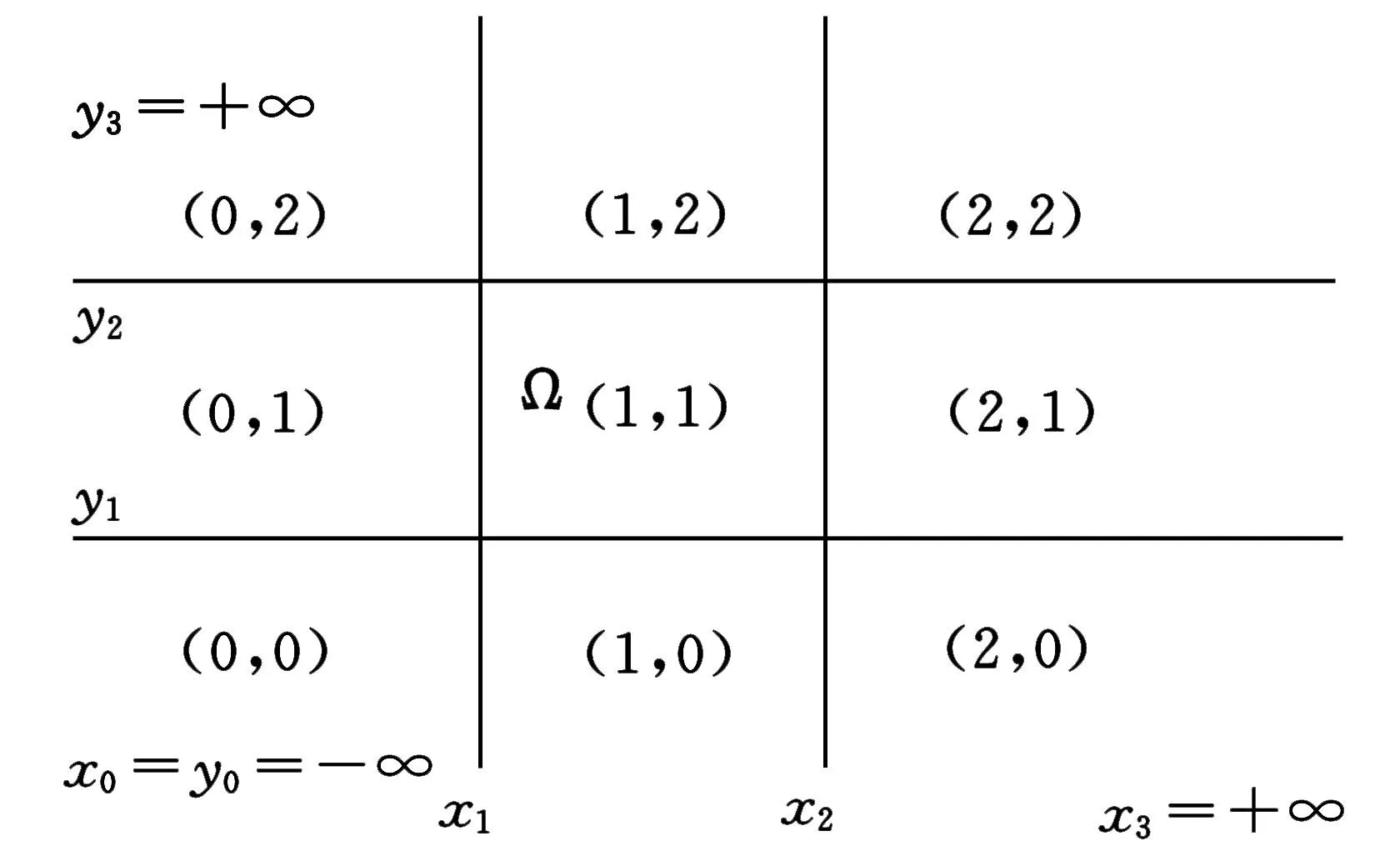
图1
为简化公式令
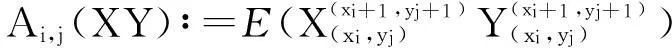

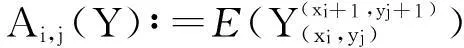
pi,j∶=P(xi 其中i,j=0,1,2.这样,(1)式所表示的条件可简写为 Ai,j(X,Y)=Ai,j(X)Ai,j(Y). 首先给出如下两个引理: 引理1在(1)式的条件下,有 Ai,0(X)=Ai,1(X)=Ai,2(X),i=0,1,2; A0,j(Y)=A1,j(Y)=A2,j(Y),j=0,1,2. 引理2在(1)式的条件下,有 pi,jpi+m,j+n=pi+m,jpi,j+n, 其中i,j=0,1,2且i+m,j+n∈{0,1,2}. 以A0,1(Y)=A1,1(Y)为例进行证明.考察区域(x0,x2)×(y1,y2)(由图1中区域(0,1)和区域(1,1)合并构成),由条件(1)式有 (2) 其中 和 将上面三个式子代入(2)式,化简可得 p0,1p1,1(A0,1(X)-A1,1(X))(A0,1(Y)-A1,1(Y))=0. 由于 A0,1(X) 所以有 A0,1(Y)=A1,1(Y), 用类似的方法可证,引理1剩下的结论也是成立的. 考察区域{x0 (3) 其中 将上面3组等式代入(3)式中化简并注意到引理1 A0,1(X)=A0,0(X),A1,0(Y)=A0,0(Y); A1,0(X)=A1,1(X),A0,1(Y)=A1,1(Y). 最终化简可得 (p0,0p1,1-p1,0p0,1)(A1,1(X)-A0,0(X))(A1,1(Y)-A0,0(Y))=0, 由于A1,1(X)-A0,0(X)>0,A1,1(Y)-A0,0(Y)>0,故 p0,0p1,1=p1,0p0,1. (4) 用上面类似的方法考察由区域(1,0)(2,0)(1,1)(2,1)构成的区域{x1 p2,0p1,1=p1,0p2,1. (5) 将(4)式与(5)式相乘 p0,0p1,1p1,0p2,1=p1,0p0,1p2,0p1,1, 消去两边的非0公共因子p1,1p1,0可得 p0,0p2,1=p0,1p2,0. (6) 同样的方法可以证明引理2剩余的结论. 由(4)式和(5)式左右分别相加可得 p0,0p1,1+p2,0p1,1=p1,0p0,1+p1,0p2,1, 在上式两边同时加上p1,1p1,0 p1,1(p0,0+p1,0+p2,0)=p1,0(p0,1+p1,1+p2,1), (7) 简化成如下分式形式 类似,有 令 (8) 借助于引理2并使用同上面类似的方法,我们可以得到如下方程组 可以证明,p0,·,p1,·,p2,·,p·,0,p·,1,p·,2就是随机变量落在相应区域内的概率: 以(8)式为例,将分式化为乘式可得 (9) 由概率可加性已知 (p0,0+p1,0+p2,0)+(p0,1+p1,1+p2,1)+(p0,2+p1,2+p2,2)=1, p1,0+p1,1+p1,2=P(x1 因此,将方程组(9)式两边相加可得 P(x1 (10) 类似,有 P(y1 (11) 最终,由(9)-(11)式有 P(x1 =p1,·p·,1=P(x1 由于{x1 4总结与结论 通常而言,两个随机变量乘积的期望等于期望的乘积并不能说明它们是相互独立的[1].但是本文发现,如果在任意概率值非零的矩形区域上标准化后的随机变量满足期望与乘积的运算可交换,那么这两个随机变量是相互独立的. [参考文献] [1]徐全智,吕恕.概率论与数理统计[M].北京:高等教育出版社,2010. A Sufficient Condition for the Independence of Two-dimensional Continuous Random Variables WANGQun1,PENGXiao-fan2 (1.School of Mechanical Electronic and Industrial Engineering,University of Electronic Science and Technology of China,Chengdu 611731, China;2. School of Mathematical Sciences,University of Electronic Science and Technology of China,Chengdu 611731, China) Abstract:We propose a sufficient condition for the independence of two-dimensional continuous random variables. This condition shows that the two-dimensional continuous random variables are independent, if the standardized random variables on any rectangular area with nonzero probability satisfy the exchangeability between the mathematical expectation and the product. Key words:independence; two-dimensional continuous random variables; mathematical expectation [中图分类号]O211.5 [文献标识码]C [文章编号]1672-1454(2015)05-0072-04 [基金项目]电子科技大学教育教学改革研究项目(Y02012023701299;2015XJYYB058) [收稿日期]2015-03-303.1 引理1证明


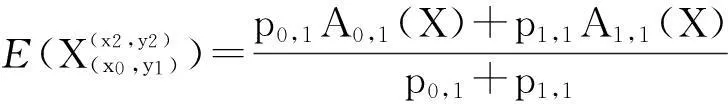
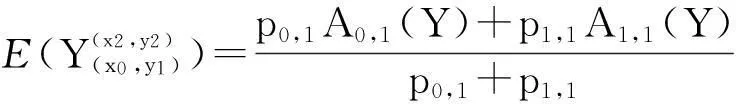
3.2 引理2证明

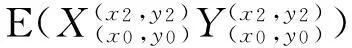

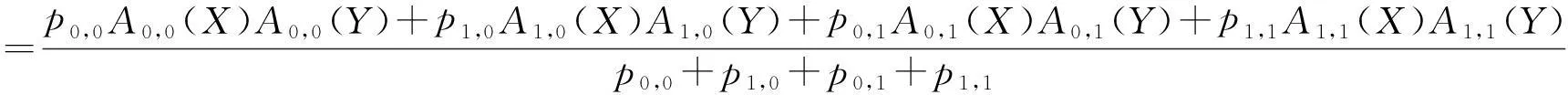
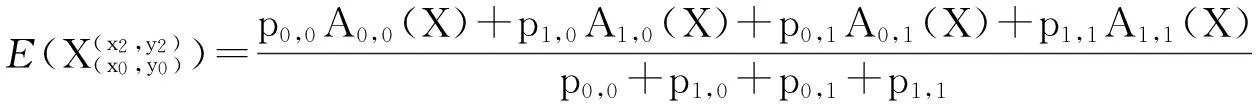
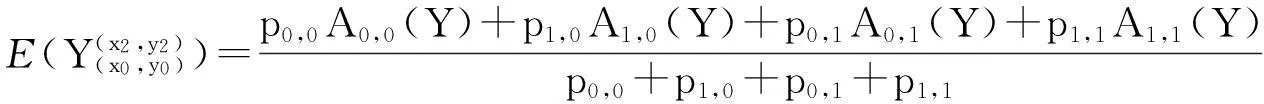
3.3 命题证明