高中生物课堂教学中数学模型的构建初探
陈敏


摘 要 在高中生物课堂推行建模教学能提高课堂教学的有效性,构建数学模型是其中重要的组成部分。构建数学模型可以化繁为简,透过现象揭示生命的本质,有助于学生的思维能力、创新能力的培养。
关键词 建模教学 数学模型 思维方式 创新能力
中图分类号 G633.91 文献标志码 B
构建模型是通过分析,舍去原型的一些次要细节、非本质联系,以简化甚至理想化的形式去再现原型的各种复杂结构、功能和联系,从而更好地解决问题。生物学经常会涉及一些抽象复杂的生命现象,这就需要通过构建模型去揭示生命现象的本质与生命活动的内在规律。生物课堂教学中建模的类型多种多样,其中数学模型是一个重要的组成部分,而且应用十分广泛。在《普通高中生物课程标准(实验)》中明确强调学生应“领悟假说演绎、建立模型等科学方法及其在科学研究中的应用;领悟系统分析、建立数学模型的科学方法及其在科学研究中的作用”。
1 数学模型的定义
数学模型是指运用数学这一学习工具,通过构建数学表达式以及能够表示数学关系的图表来揭示其中所隐藏的规律,并且能够预测将来的发展趋势。高中生物教材中涉及到大量的需要运用组合学、数理统计学、概率论、函数等知识来解决的生物问题,所以需要教师根据教材,适时地引导学生通过构建数学模型,将扑朔迷离的生物问题转换为简洁明了的数学“语言”,从而大大提高生物课堂教学的有效性。
2 数学模型的构建方法
2.1 运用组合学知识构建数学模型
在学习人教版生物教科书《必修2·遗传与进化》中“基因是有遗传效应的DNA片段”这节课,探究脱氧核苷酸序列与遗传信息多样性之间关系时,教师可以根据由简到繁、循序渐进的原则,先创设具体的数字化情境,然后引导学生从中发现规律,建立数学模型,领悟数学模型背后所蕴含的更深层次的生物现象或特性。例如教师可以设置下列的数字化情境:长度为10个碱基对的脱氧核苷酸序列可以有多少种的排列方式?那么100个碱基对、1 000个碱基对、n个碱基对呢?如果不同的排列方式都代表不同的基因,那么可以得出基因具有什么特性呢?这些问题引导学生应用数学课学习过的排列组合知识,通过亲自动脑、动手发现基因排列组合方式的表达式4n,其中4为碱基配对方式,n为碱基对的数目,并且从具体的数字化情境深刻领悟到基因的多样性。学生在小试牛刀的过程中,打破了学科之间看似无法逾越的鸿沟,品尝到了用数学的思维方式、方法解决生物学问题的成功的喜悦。同样的方法还可以应用在“基因的表达”这一节的探讨mRNA上的碱基与氨基酸之间的对应关系的过程中。
2.2 运用数理统计学知识构建数学模型
在高中生物课堂上运用数理统计学知识构建数学模型,简单地说就是指本着实事求是的原则,通过切实有效的方法收集数据、对数据进行合理地处理、推理,并进行统计分析,构建数学模型,以便对生物问题进行推断或预测,甚至提出相应的对策或建议。
在人教版生物教科书《必修3·稳态与环境》的“种群的特征”中,调查种群密度的样方法和标志重捕法都是运用数理统计学的方法。特别是在学习标志重捕法时,教师注重要引导学生思考:标志重捕法的原理是什么?它是依据什么来估算种群的数量,进而计算出种群密度的?假设N为种群数量,M为第一次标志数,m为重捕的标志数,n为重捕个体数,是否能构建出计算种群数量的数学表达式?当学生自主构建数学表达式M/N=m/n后,教师在给予适时的赞扬和鼓励的同时紧接着抛出问题:如果在调查期间由于有的标志物脱落,或者标志物过于醒目影响标志对象正常的生活,或者调查期间有大规模的迁入和迁出、出生和死亡等,那么所得出的种群密度与真实值相比是偏大还是偏小?从而让学生在已构建的数学模型的基础上,进一步认识到标志重捕法得到的种群数量和种群密度并非就是真实值,但在满足相关条件的前提下,可以无限接近真实值。
2.3 运用概率知识构建数学模型
概率是指随机事件或现象在相同条件下大量重复发生过程中所呈现的一种数量上的规律。
人教版生物教科书《必修2·遗传与进化》中的“孟德尔的豌豆杂交实验(一)”是开启学生探索生物遗传变异奥秘之路的重要的一节,教师要把握好这个机会培养学生运用概率论知识构建数学模型来解决生物问题。例如,在孟德尔一对相对性状的实验中,为什么雌雄配子的随机结合会导致F1自交后代出现3∶1的性状分离比呢?“性状分离比的模拟实验”中,在学生充分了解实验原理的基础上,教师将班级学生进行分组实验,抓取次数分别为10、15、20、25、30……,要求每个小组设计记录表格(表1),真实地记录实验数据。实验结束后,让小组代表汇报统计结果,结果发现有的小组的统计结果接近3∶1,而有的小组的统计结果出现了严重的偏差。这时,教师鼓励这些小组积极寻找实验失败和成功的可能原因。然后教师再让学生将所有小组的抓取次数、各组合的数量相加,统计DD、Dd、dd的数量及性状分离比,分析结果。最后,教师进一步提出问题:“如果当年孟德尔只做了少量的豌豆杂交实验是否能发现分离定律呢?”
这个模拟实验可以让学生体会到一个抽象的生物问题可以通过构建数学模型轻而易举地得以解决,同时也让学生懂得要获得一个事件发生的真实概率,应该要在尊重实验数据的基础上,尽可能地增加实验重复的次数。让学生领悟孟德尔两大遗传定律F2代所出现的3∶1的性状分离比是建立在科学家进行的大量实验的基础上,同时提高了学生对实验结果偏离真实情况的分析能力。
2.4 运用函数知识构建数学模型
函数是中学数学学习的重点和难点,一名高中学生已经学习并掌握了多种函数的一般性质和图像。教师可以充分利用这一优势,培养学生用函数式及曲线构建数学模型将一些复杂繁乱的生物问题变得简单形象,且可以预测。
例如,在人教版生物教科书《必修2·遗传与进化》的“杂交育种与诱变育种”中,植物杂交育种常用的方法是杂交→自交→选种→自交→不发生性状分离。在“选种→自交→不发生性状分离”的教学过程中,教师可以创设问题情境,由浅入深地引导学生进行思考讨论。
师:选种是根据表现型还是根据基因型?
生:表现型。
师:表现型符合的个体是否就一定能稳定遗传?
生:不一定。
师(追问):如果育种目的是要获得能稳定遗传的显性个体,那么在选种之后要怎么做才能使后代杂合子的比例降至最低呢?
学生相互讨论。
教师在解决问题的思路上进行适当的引导和点拨。
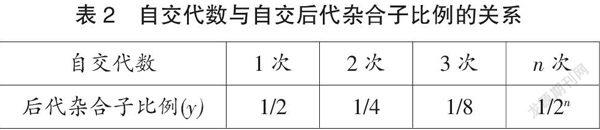
师:以杂合子(Aa)逐代自交为例,请大家完成表2,并写出自交代数与自交后代杂合子比例之间的函数表达式。
师:请写出自交n代数纯合子、显性(隐性)纯合子所占比例的函数表达式。
生:y=1-1/2n。
师:请大家用坐标图以曲线的形式来表示自交代数n与自交后代杂合子、纯合子以及显性(隐性)纯合子所占比例之间的关系。
生:a-纯合子比例,b-显性(隐性)纯合子比例,c-杂合子比例(图1)。
师:从曲线图大家可以发现什么规律?能否理解选种后不断自交的意义?
生:随自交代数的增加,杂合子比例在不断减小,纯合子的比例在不断增加,直至不发生性状分离,得到的将都是纯合子。
教师在这部分知识的教学中,主要扮演引导者的角色,通过设置问题情境,循循善诱地引导学生去发现问题、分析问题和解决问题。通过构建函数表达式并将函数表达式转换为直观形象的坐标图完成杂合子自交的数学模型的构建,使学生对植物杂交育种的基本方法不仅知其然而且还知其所以然。
3 不同数学模型之间的相互转换
在生物课堂教学的过程中可构建的数学模型是多种多样的,如函数表达式、表格、坐标图、饼状图、直方图等。一种教学内容并非只能对应一种类型的数学模型。在建模教学中,教师除了要逐步培养学生构建数学模型的能力,还要培养学生用多种不同的数学模型来表示同一个生命现象,让建模真正成为学生提高分析问题、解决问题的手段。
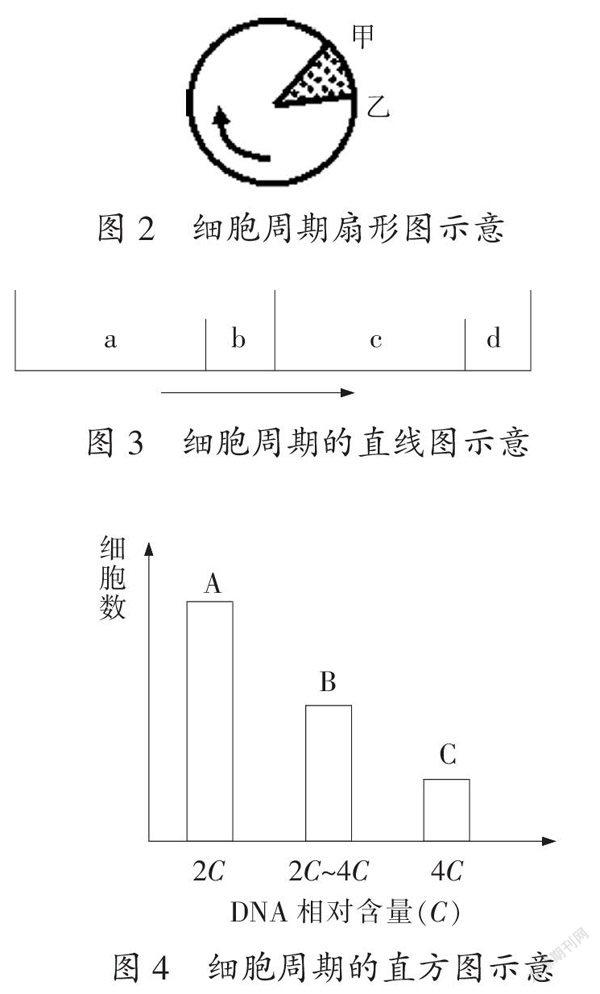
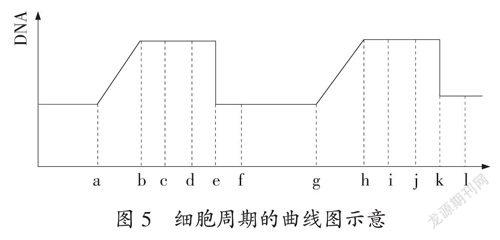
例如,高中生物人教版生物教科书必修1的“细胞的增殖”这一节中,细胞生长和增殖的周期性是教学重点,而对细胞周期这个概念的正确理解是学习有丝分裂的基础。教材中分裂间期、分裂期和细胞周期三者之间的关系是以扇形图(图2)的模型呈现,教师可以让学生尝试以直线图(图3)来展示三者之间的关系,从学生的模型构建中了解学生对分裂间期和分裂期在时间上的先后顺序以及占细胞周期的比例的理解和掌握的情况。在学习完有丝分裂的全过程后,教师可以让学生构建直方图(图4)和曲线图(图5)来表现一个完整的细胞周期。在教师层层深入地引导学生构建多种的数学模型的过程中,促进了学生对知识的内化,达到举一反三、触类旁通的效果。
在生物课堂教学过程中构建数学模型,需要教师的循循善诱,虽然会占用较多的教学时间,但是一堂课的有效性并不是取决于教师传授给学生多少课本知识,而在于学生通过这堂课的学习是否能灵活应用知识并且形成解题技巧。教师在高中生物课堂教学中实行建模教学,可以激发学生的学习兴趣,对培养学生的创新意识、发散型思维以及科学探究能力起到积极的作用。

