采用压缩感知的直扩测控信号处理*
程艳合
(1.解放军装备学院 光电装备系,北京 101416;2.北京航天飞行控制中心,北京 100094)
采用压缩感知的直扩测控信号处理*
程艳合1,**2
(1.解放军装备学院 光电装备系,北京 101416;2.北京航天飞行控制中心,北京 100094)
摘要:鉴于扩频测控系统宽带化带来的高速采样压力和高数据率问题,研究了基于压缩感知的直扩测控信号处理方法。通过深入分析直扩测控信号稀疏性,构造了延时-多普勒基字典,提出了基于压缩感知直扩测控信号处理框架,并针对直扩测控信号特点给出了改进正交匹配追踪重构算法,最后针对该信号处理方法的可行性和性能分别进行了仿真实验。仿真结果不仅验证了方法的可行性,同时表明可以在不影响解调性能条件下大幅度降低采样率或数据率,并具有一定的降噪效果,这将为直扩测控通信系统提供一种高效的模数转换和同步解调处理方式。
关键词:直扩测控信号;压缩感知;延时-多普勒基字典;伯努利随机矩阵;改进正交匹配追踪算法
doi:10.3969/j.issn.1001-893x.2015.02.003
引用格式:程艳合,杨文革,张令军.采用压缩感知的直扩测控信号处理[J].电讯技术,2015,55(2):129-134.[CHENG Yanhe,YANG Wenge,ZHANG Lingjun.DS TT&C Signal Processing Based on Compressive Sensing[J].Telecommunication Engineering,2015,55(2):129-134.]
中图分类号:TN911.7
文献标志码:码:A
文章编号:号:1001-893X(2015)02-0129-06
收稿日期:*2014-10-11;修回日期:2014-12-26Received date:2014-10-11;Revised date:2014-12-26
Abstract:In view of the high-speed sampling and high data rate pressures which come from broadband of the direct-sequence spread-spectrum tracking,telemetry and command(DS TT&C) system,a DS TT&C signal processing method based on compressive sensing(CS) is provided.Firstly,the delay-Doppler basic dictionary is built by in-depth sparse analysis of DS TT&C signal.Then,a DS TT&C signal processing framework based on CS is proposed,and the improved orthogonal matching pursuit(OMP) algorithm is provided referring to the signal.Finally,the feasibility and performance of the proposed method are investigated by simulation experiments.The results show that the method is feasible,and the sampling or data rate can be greatly reduced without degrading the demodulation performance,moreover,it can get some noise deduction effect.The technology will provide a more efficient analog digital conversion and synchronous demodulation method for DS TT&C system.
作者简介:
DS TT&C Signal Processing Based on Compressive Sensing
CHENG Yanhe1,YANG Wenge1,ZHANG Lingjun2
(1.Department of Optical and Electronic Equipment,The Academy of Equipment,Beijing 101416,China;
2.Beijing Aerospace Flight and Control Center,Beijing 100094,China)
Key words:DS TT&C signal;compressive sensing;delay-Doppler basic dictionary;Bernoulli random matrix;improved OMP algorithm
1引言
扩频体制由于自身的抗干扰性、隐蔽性、多址复用和可任意选址等优点受到了航天测控通信领域的广泛重视,统一扩频测控通信系统应运而生[1]。在统一扩频体制中,为了应对日益激烈的空间信息对抗形势,并获得更高的测距精度,系统扩频带宽进一步增大,给接收机前端A/D提出了很高要求,致使接收机按照Nyqiust采样定律进行采样变得非常困难[2]。另一方面,即使测控系统能够以Nyqiust速率进行采样,带宽的增加意味着数据率的提高,系统将面临高数据率问题,而且高数据率会给后续传输、记录存储和同步解调处理带来沉重负担。因此,有必要研究一种能够降低采样速率或者解决高数据率问题的方法。
近年来,出现了一个全新的信号处理理论,即压缩感知(Compressive Sensing,CS)。该理论突破了传统的Nyquist采样理论框架,目前已经广泛应用在雷达成像、模式识别和信号估计等研究中[3]。在测控通信领域,文献[4]将压缩理论应用到标准测控通信信号处理中,研究了信号的压缩测量与重构问题,但是没有涉及测控通信中带宽更宽、数据冗余更大的扩频测控信号。
本文将压缩感知理论应用于直扩测控(Direct-sequence Spread-spectrum Tracking,Telemetry and Command,DS TT&C)通信信号的处理中,首先分析了DS TT&C信号的稀疏性,然后给出了基于CS的DS TT&C信号处理框架,最后仿真验证了压缩感知理论不仅可以实现信号的重构,而且具有一定的降噪效果。
2压缩感知原理
对于长度为N的信号x,若信号本身不稀疏,假设存在一组变换基字典Ψ(其列向量Ψi为基原子向量),使得x在该变换基字典上是K-项稀疏的,即有x=Ψs[3],其中s是稀疏信号。压缩感知基本原理如图1所示,则有测量过程可表示为
y=Φx=ΦΨs=Θs。
(1)
式中,Φ∈CM×N是测量矩阵,Θ=ΦΨ∈CM×N是感知矩阵。据上可以给出原信号压缩比定义:
γ=M/N。
(2)
式中,N是信号长度,M是压缩测量值个数。文献[5]证明了如下结论:当感知矩阵Θ满足有限等距性(Restricted Isometry Property,RIP)时,信号x可以通过0-范数下优化求解从测量值y中精确重构,即
min‖s‖0s.t.y=Θs。
(3)
式中,‖·‖p是p-范数。

图1 压缩感知原理框图
有限等距性条件是信号重构的重要基础,其定义为:若对所有满足‖s‖0≤K的稀疏信号s,矩阵Θ都满足

(4)
式中,K是信号稀疏度,等距常数δK是保证式(4)成立的最小值,且δK∈(0,1),则称Θ满足参数为(K,δK)的RIP条件。δK具有单调性,对任意两个K1≥K2,有δK1≥δK2。若观测向量长度为
M=cK×lg(N/K)≪N。
(5)
式中,c是常数因子。如果式(5)成立,矩阵Θ以高概率满足RIP条件。在实际中,信号中一般存在噪声,可将式(5)扩展为
min‖s‖0s.t.‖y-Θs‖2≤δ。
(6)
式中,δ是信号噪声功率。
综上可知,压缩感知理论包括稀疏基字典Ψ、测量矩阵Φ、重构算法三部分主要内容。
3DS TT&C信号稀疏性分析
信号稀疏性是压缩感知理论应用的重要前提和理论基础。信号的稀疏性内容(即信号稀疏性分析)具体体现在设计合适的稀疏基字典,使得信号在该基字典所表示的变换域中最稀疏[6]。
常见的DS TT&C体制是脉冲编码调制-码分多址-二相相移键控(Pulse Code Modulation-Code Division Multiple Access-Binary Phase Shift Keying,PCM-CDMA-BPSK),在未加噪声情况下,接收机的接收信号数学模型可表示为[1]
x(t)=AD(t-τ)P(t-τ)exp(j(2π(fc+fd)t+θ))。
(7)
式中,A是载波振幅;P(t)是码速率为Rc扩频波形;D(t)是比特率为Rb数据波形,且有Rb=1/Tb≪Rc=1/Tc;fc是中频频率;τ是码相位,即传输时延;fd是多普勒频率;θ是载波初始相位,为简化后续理论分析使θ=0。
根据式(7)及DS TT&C信号特性易知,该类信号是时域连续波信号在时域不具有自身稀疏性,即该类型信号不是自身稀疏信号,而且其频谱被扩展,在频域也不具有明显的稀疏性。因此,本文从DS TT&C信号稀疏基字典构造着手,研究该类信号的字典稀疏性。
DS TT&C系统采用的扩频波形P(t)可以具体表示为

(8)



(9)
式中,D[k]是数据位,KD是处理信号时长包含的数据位数,Tb是标准位时长,且有
ψk,τ,fd(t)=P(t-τ-kTb)exp(j(2π(fc+fd)t))。
(10)
为了便于后续分析,以Nyqiust采样频率fs对式(9)进行离散化如下:

(11)
式中,Ts是采样时间间隔,n∈[1,N],N是KD位数据对应的Nyqiust采样点数。根据Nyqiust采样定理可知,式(11)所示离散化信号可以等效表达式(9)所示信号,后续分析与仿真都基于该等效离散化信号形式。值得注意的是,根据式(11)可知信号稀疏度与处理时长包含的数据位数KD保持一致。
已知函数ψk,τ,fd由传输时延τ、多普勒频率fd和对应数据位k确定,可以把ψk,τ,fd看作字典原子,通过离散化τ和fd对其进行扩充,可得基于信号模型分析的延时-多普勒基字典ΨS,具体表示如下:

(12)

4基于CS的DS TT&C信号压缩处理框架
在研究DS TT&C信号稀疏性基础上,利用压缩采样器直接对信号进行压缩采样,或者对已经按照Nyquist采样得到的数字DS TT&C信号进行压缩处理,可以降低模拟信号采样率或数字信号数据率,缓解传输、记录存储压力,所得到的是压缩状态数字信号,可以通过重构算法对其进行重构,并进行同步解调获得所需信息,如图2所示。

图2 基于CS的DS TT&C信号处理框架
4.1 信号压缩测量
在压缩感知理论框架中,对信号的压缩测量实质上是一个投影的过程,也就是将具有稀疏性的长度为N的原始信号直接投影到一组测量基(即测量矩阵)上,得到M(M< 在压缩感知应用过程中,较为常见测量矩阵包括高斯随机矩阵、伯努利随机矩阵,其中高斯随机矩阵在理论分析和数字域数据压缩处理中应用最为广泛,具备理论上的完美特性,但是它在实际系统中的硬件实现存在较大困难,所以不适用于模拟信号压缩采样;相对而言,虽然伯努利随机矩阵的理论完美性比高斯随机矩阵差一些,但是该矩阵硬件实现比较容易,可以通过线性反馈移位寄存器实现。因此,压缩采样相关研究基本都基于伯努利随机矩阵或者其扩展形式而展开,目前主要包括随机调制压缩采样、多带调制压缩采样等[7]。为了同时适应模拟信号压缩采样和数字信号压缩降维,本文采用伯努利随机矩阵作为测量矩阵进行后续仿真验证。 重构算法是整个信号处理流程中至关重要的一个组成部分,对信号的重构精确度有着很大的影响。压缩感知中的信号重构过程就是从M个观测数据点中对长度为N(M< 针对此类问题的一类有效方法是贪婪迭代类重构算法。该类算法的核心思想是通过每次迭代时选择一个局部最优解来逐步逼近原始信号,最终实现信号重构,其中OMP算法[9]是最常见的一种贪婪迭代算法,后续很多算法都是在其基础上的进一步改进。根据前文DS TT&C信号的稀疏性分析可知,信号的稀疏度与处理时长包含的数据位数保持一致,据此可以得出基于OMP算法的DS TT&C信号重构算法,描述如下: 输入:测量矩阵Φ,DS TT&C信号参数,处理时长包含数据位数KD,信号压缩测量向量y; 初始化:残差r0=y,支撑集Λ0=∅,迭代次数t=1; 循环步骤: (1)根据式(10)和式(12),构造稀疏基字典ΨS,并计算传感矩阵Θ=ΦΨS; (3)更新支撑集Λt=Λt-1∪{λt},并存储找到的传感矩阵原子列向量Θt=[Θt-1,φλt]; (6)若t≥KD,停止迭代过程;若不满足则t=t+1,继续执行步骤2。 5仿真实验 对上述DS TT&C信号压缩处理方法进行实验验证,主要思路是通过原始信号和重构信号对比来研究本文提出方法的性能。仿真实验分为可行性验证和性能分析两个阶段。 可行性验证主要是验证基于CS的DS TT&C信号处理方法可行性,因此暂不考虑噪声情况,在一定观测数量(压缩比)情况下,对比分析信号压缩前和重构后结果。 在仿真实验中,数据率Rb为10 kbit/s,伪码周期1023,码速率Rc为10.23 MHz,中频fc为14 MHz,采样率fs=56 MHz,传输延时量化精度Δτ=Ts,多普勒频率量化精度Δfd为5 Hz,延时适用范围[0,1/Rb],多普勒适用范围[-1000,1000]Hz,信号分段处理长度取KD=8,则有对应的Nyqiust采样值个数N为44 800,压缩比γ=0.1,结果如图3所示。 (a)时域对比 (b)频域对比 从压缩重构信号的时域波形和频域频谱结果可以看出,基于延时-多普勒基字典,观测数量为原始信号长度的1/10(即压缩比为0.1)时,重构误差很小(如图3所示),即信号压缩重构效果很好。 在信号压缩重构后,对重构数据进行后续的解调处理,并与原信号信息码元进行对比,如表1所示,可以看出,解调得到的信息码元全部正确。 表1 压缩重构判决码元与原始信息码元比较 综合上述分析可以认为,在应用延时-多普勒基字典和伯努利随机测量矩阵时,能够实现对DS TT&C信号的压缩重构,从重构的信号数据中可以实现正确的解调处理,从而实现了本文提出方法的可行性验证。 为了定量描述,首先定义信号压缩重构的时、频域相对误差如下: (13) (14) 性能分析主要从两方面进行,首先不考虑噪声,仿真分析压缩重构性能受观测数量变化的影响规律,用信号压缩重构相对误差表征压缩重构性能;其次,选定一个压缩比,仿真分析重构性能受噪声变化的影响规律。 考虑到采用的测量矩阵即伯努利随机矩阵具有一定随机性,为避免某次测量矩阵性能不佳而对压缩重构效果产生影响,对每种情况都重复实验100次。压缩比变化范围为γ=[0.001,1],信噪比变化范围取[-50 dB,50 dB],结果如图4和图5所示。 (a)时域 (b)频域 (a)时域 (b)频域 由图4可知,随着压缩比增大,即压缩观测数目增大,信号的时域、频域相对误差变化趋势一致:在低压缩比时,相对误差较大;当压缩比增大到0.004时,相对误差急剧降低;在高压缩比时,相对误差基本保持不变,保持在10-6左右。由图5可知,压缩重构信号与带噪原信号的时域、频域相对误差随信噪比变化趋势一致:在低信噪比时,相对误差较大,保持在1左右;当信噪比增大到-10 dB时,相对误差缓慢降低;当信噪比小于16 dB时,相对误差都保持在0.1以上。但原信号中噪声不仅对于后续的同步解调处理无用,而且会降低同步解调性能,因此没有必要恢复原信号中的噪声分量。下面考察压缩重构信号与相对应的加噪前原信号相对误差变化情况,如图6所示。由图6可知,重构信号与相对应的加噪前原信号时域、频域相对误差随信噪比变化趋势也保持一致:在低信噪比时,相对误差较大,保持在1左右;当信噪比增大到-20 dB时,相对误差快速降低;当信噪比大于-5 dB时,相对误差都保持在0.1以内。 (a)时域 (b)频域 通过以上的仿真实验,可以得出以下结论: (1)DS TT&C信号在延时-多普勒基字典上具有较强的稀疏性,基于该基字典和伯努利随机测量矩阵,不仅能够实现对DS TT&C信号的压缩重构,而且从重构信号数据中可以实现正确的解调处理; (2)在无噪声情况下,当压缩观测数量是原信号的0.4%时,重构相对误差保持在10-6左右,基本可以忽略,可认为此时原信号得到了很好的恢复; (3)在有噪声情况下,压缩重构信号与带噪原信号相对误差较大,但是相对于后续同步解调比较关注的加噪前原信号的误差较小,当信噪比大于-5 dB时,保持在0.1以下。这也同时反映了本文提出的DS TT&C信号处理方法具有一定的降噪效果。 6结论 本文将压缩感知理论应用于DS TT&C信号的处理中,基于所构造的延时-多普勒基字典,提出了基于CS的DS TT&C信号处理框架。仿真分析表明,本文所提方法能够在不影响后续同步解调性能的前提下,将所需要的采样率或数据率大幅度降低至原采样率的1%左右,并且具有一定的降噪效果。后续将进一步深入探讨基于CS的DS TT&C信号同步解调处理,以及该类型信号处理框架的硬件实现等相关问题。 参考文献: [1]刘嘉兴.飞行器测控与信息传输技术[M].北京:国防工业出版社,2011. LIU Jiaxing.Spacecraft TT&C and Information Transmission Technology [M].Beijing:National Defense Industry Press,2011.(in Chinese) [2]杨小牛,楼才义,徐建良.软件无线电技术与应用[M].北京:北京理工大学出版社,2010. YANG Xiaoniu,LOU Caiyi,XU Jianliang.Software Radio Technology and Application [M].Beijing:Beijing Institute of Technology Press,2010.(in Chinese) [3]Kazunori H,Masaaki N, Toshiyuki T.A user′s guide to compressed sensing for communications systems [J].IEICE Transactions on Communications,2013,96(3):685-712. [4]黄凌.采用压缩感知的标准测控信号处理[J].电讯技术,2014,54(5):578-583. HUANG Ling.A TT&C signal processing method based on compressed sensing [J].Telecommunication Engieering,2014,54(5):578-583.(in Chinese) [5]Donoho D L.Compressed Sensing[J],IEEE Transactions on Information Theory,2006,52(4):1289-1306. [6]Rubinstein R,Bruckstein A, Elad M.Dictionaries for sparse representation modeling [J].Proceedings of the IEEE,2010,98(6):1045-1057. [7]Cantles E I,Wakin M B.An introduction to compressive sampling [J].IEEE Signal Processing Magazine,2008,25(2):21-30. [8]Mohammad R M,Emad F, Mohammad H M.Non-negative sparse decomposition based on constrained smoothed0 norm [J].IEEE Transactions on Signal Processing,2014,100(7):42-50. [9]Wang J,Kwon S, Shim B.Generalized orthogonal matching pursuit [J].IEEE Transactions on Signal Processing,2012,60(12):6202-6216. 程艳合(1987—),男,河北衡水人,博士研究生,主要研究方向为航天测控技术、扩频信号处理、压缩感知理论; CHENG Yanhe was born in Hengshui,Hebei Province,in 1987.He is currently working toward the Ph.D. degree.His research concerns aerospace TT&C technology,spread spectrum signal processing and compressive sensing. Email:cheng20130810@foxmail.com 杨文革(1966—),男,江西金溪人,教授、博士生导师,主要研究方向为空间飞行器测控与通信系统、压缩感知理论; YANG Wenge was born in Jinxi,Jiangxi Province,in 1966.He is now a professor and also the Ph.D. supervisor.His research interests include spacecraft TT&C and communication system and compressive sensing. 张令军(1972—),男,山东沾化人,工程师、博士研究生,主要研究方向为信息系统、计算机工程。 ZHANG Lingjun was born in Zhanhua,Shandong Province,in 1972.He is now is an engineer and currently working toward the Ph.D. degree.His research concerns information system and computer engineering.4.2 信号重构

5.1 可行性验证

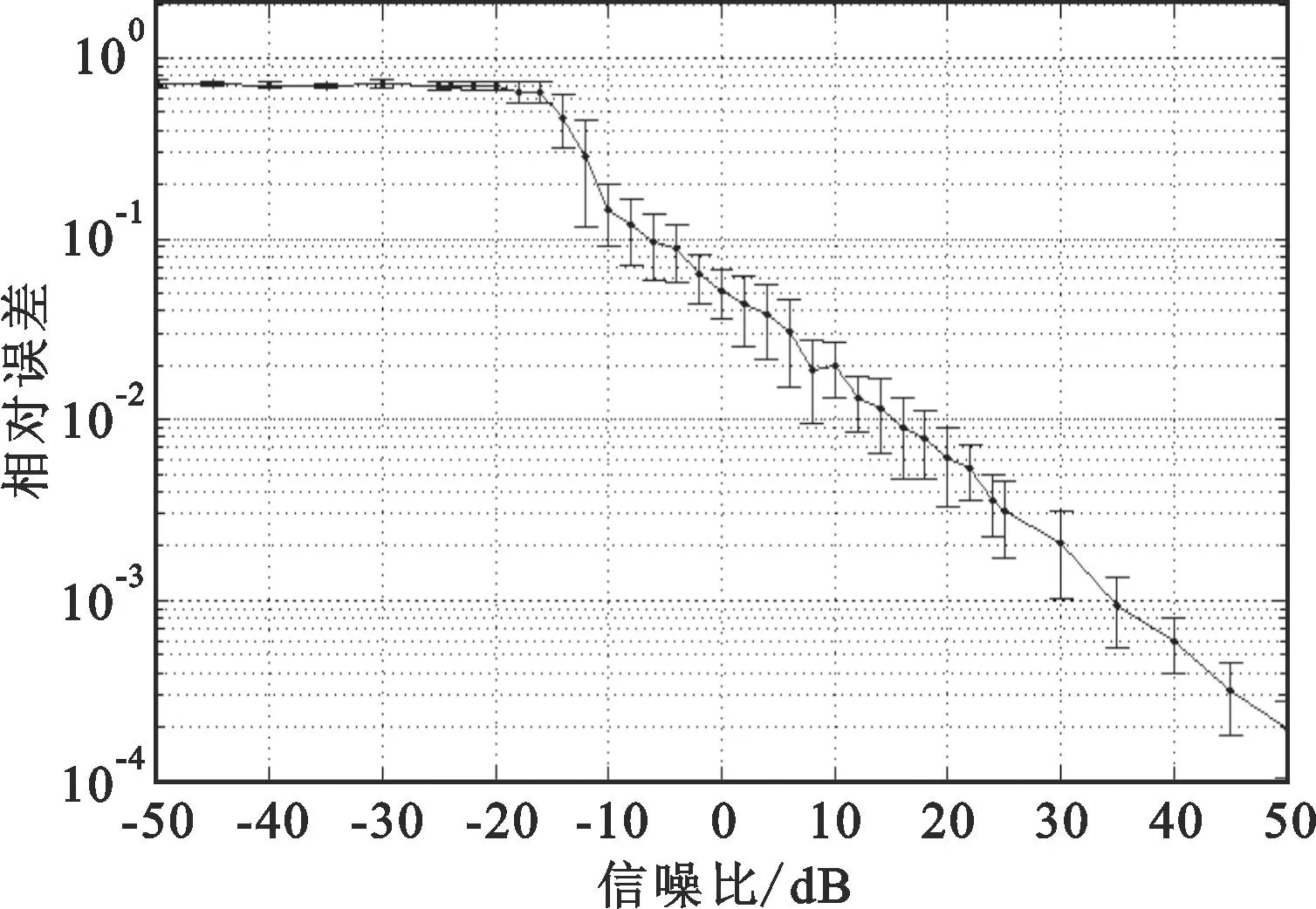
5.2 性能分析






5.3 仿真实验总结


