一种海洋蒸发波导通信带限信道建模方法*

肖金光，周新力，张 烨

(海军航空工程学院电子信息工程系，山东烟台264001)

1 引言

海面上蒸发波导(Evaporation Duct，ED)发生概率较高，能够陷获频率和仰角满足一定条件的电磁波，形成超视距传播，对于雷达探测、通信、电子对抗以及低高度武器或平台的攻防都具有重要意义。其中利用波导进行通信可行性已被美、澳大利亚等开展的试验所证实，对其性能的研究和系统设计也在持续开展[1－2]。射线追踪法(Ray Tracing，RT)作为一种基于几何光学理论的高频近似方法，虽然对衍射和散射的忽略造成了场强计算误差，但估计多径时间上具有明显优势，因而成为一种非常流行的预测无线信道特性的方法[3]。文献[4]给出了基于幅度和多径延迟时间的信道传输函数，但未考虑海面的反射作用。文献[5]基于RT，计算了多径延迟和到达信号幅度，幅度计算中用粗糙因子修正表面反射造成的场强衰减，但未考虑电波的传播扩散，且给出了波导强度而不是大气折射率剖面，亦即求解多径时间时未考虑射线在非均匀大气中传播速度的不均匀。文献[6]基于容量有限的Markov生灭过程研究大气波导中到达接收站的射线径数，利用MUSIC算法对多径到达角进行最佳估计。

综上所述，基于RT的蒸发波导通信研究中，场强计算和多径特性估计存在诸多问题有待解决。本文对蒸发波导通信带限信道建模信号的场强计算、多径特性、蒸发波导超视距通信系统设计使用策略、带限冲激响应方法进行了研究，并进行了数值试验。

2 基于SRT的蒸发波导信道建模方法

2.1 分段射线追踪法

RT认为电磁波在非常小的射线管内传播，跟踪每一条射线传播轨迹，有传统积分和泰勒级数近似两种模式。鉴于海洋蒸发波导高度一般不高于40 m，且本文的研究重点是电波的超视距传播问题，因此选用适于低仰角电波传播计算的泰勒级数近似法。

对大气折指数n引入平坦地球近似，将电波沿地表的传播等效为水平传播，则修正大气折射指数为

式中，re为地球半径。修正大气折射率M为

设 r1、h1、a1和 r2、h2、a2分别为射线初始位置和到达位置的距离、高度及仰角，ΔM为折射率变化量，g为修正折射率M在分层内的线性变化率，RT的求解公式组为

在某一折射率分层内部，上述射线的轨迹就会有三种情况:单调向上、单调向下或者在层内拐弯(达到最高或最低点)。如果进入别的分层则以进入点作为终点，而对于层内拐弯射线(根据初始点和终点的角度符号相反可以判断)，从最高点或最低点处拆成两段分别计算。这样就统一成单调向上和向下两种情况，这种大气分层条件下分段射线追踪(Subsection Ray Tracing，SRT)计算方法，既简化了运算，又便于进行传播路径长度和时间的计算。

单调向上和层内达到最高点两种情况如图1所示，而单调向下和层内达到最低点的情况具有与图1对称的形式。

图1 分段射线追踪Fig.1 Subsection ray tracing

从而，根据式(3)～(5)可以由射线初始位置、高度、仰角以及折射率分层情况，求得射线通过的路径。

2.2 蒸发波导模型和电波陷获传播条件

中性大气层结中蒸发波导的大气修正折射率剖面为[7]

式中，表面粗糙参数z0为1.5×10－4m，d为蒸发波导高度(单位为m)，M(z0)取为330。若取蒸发波导高度30 m，天线高度25 m，基于SRT的射线轨迹如图2所示(只绘出了超视距传播的射线)。

图2 射线轨迹Fig.2 Tracks of rays

对于一定强度/高度的波导，频率大于某一截止频率fmin(即波长小于某一截止波长，单位Hz)的电磁波才能形成陷获传播，如图3所示。截止频率与波导高度的近似关系可以表示为[8]

图3 最低陷获频率Fig.3 Minimum trapped frequency

2.3 海洋蒸发波导中电波传播计算

基于前面给出的大气分层条件下SRT计算方法，可以方便地计算射线的路径长度。射线弧与水平位移长度之差ΔS和射线长度S分别为

电波在某段路径上的传播时间Δt由射线长度s及传播速度v决定:

式中，c0为真空波速。电波强度由初始场、粗糙面反射系数、空间扩散决定，到达强度由接收球法确定。初始场为E(φ)=f(φ)E0，其中f(φ)为角度 φ 射线对应的天线方向图增益系数，全向天线时为1。空中传播射线的场强为E2=E1eiks/s，达到地表射线反射前后的场强关系为E2=ΓE1，其中Γ为菲涅耳反射系数，是入射余角的函数(由射线在表面上的入射余角决定)[9]。因此，假设射线发生L次反射，则射线经过路径S后的场强为

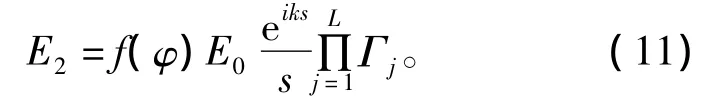
二维空间上某点的场强为所有到达接收球射线的强度和，接收球半径R取为[3]

式中， 为辐射源出发相邻射线的张角，单位为rad。多径信号的接收球法，需要清晰地区分各路径，然后针对每一路径族，使用接收球法计算该路径的信号强度，不妨称之为分离多径信号族接收球法。

2.4 蒸发波导带限信道建模方法

由图1可知，蒸发波导中，射线经不同路径到达接收位置，是典型的多径信道，其复低通等效冲激响应可以描述为[4]

式中，Ei和τi分别为第i条路径到达信号的幅度和到达时间，Ft、Fr为发收天线方向图量化因子，θt为射线初始角，θr为到达角。若收发天线均采用通信常用的全向天线时，Ft和Fr均为1，则式(13)可简化为

蒸发波导中的超视距通信不存在强度占绝对优势的视距路径。为了防止多径时延对接收造成不可逆的影响，信号符号周期Ts与最大多径时延τmax需要满足

为避免多径引起的频率选择性衰落，系统相干带宽Δf可取为

τmax决定了可通信道的最大带宽，相当于频域加窗，等效于时域乘以sinc函数，因此复低通表示的信道带限冲激响应为

3 信道特性仿真分析与建模

从源点±1°夹角内等间隔发射3000条射线，蒸发波导高度30 m，海面风速5 m/s，发射天线高度10 m、20 m和25 m时，电波到达100 km处的高度与时延分布关系如图4～6所示。

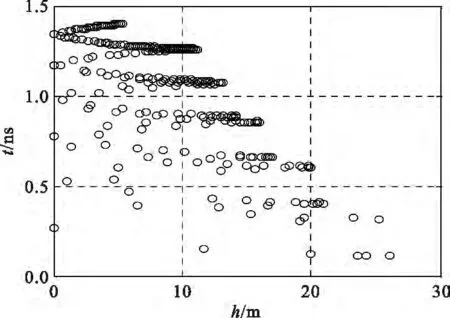
图4 10 m发射天线的多径信号时延分布Fig.4 Distribution of multipath signal delay with radiating antenna at 10 m

图5 20 m发射天线的多径信号时延分布Fig.5 Distribution of multipath signal delay with radiating antenna at 20 m

图6 25 m发射天线的多径信号时延分布Fig.6 Distribution of multipath signal delay with radiating antenna at 25 m

由图7可知，增加射线数只是增加了到达接收位置射线的密度。因为由原点出发射线的初始角是连续小角度变化的，相邻射线经历的传播路径差异不大，导致到达信号的强度、到达时间、到达角、到达高度连续变化。增大射线条数即减小初始角变化量，表现为到达信号参量的插值，这正说明了式(12)接收球法进行场强计算的原理。虽然不用置疑的是RT忽略的衍射造成了误差，但对于蒸发波导超视距多径信号，重要的是各径信号的相对强度。为了适应蒸发波导高度随气象条件的变化，保证较高的可通率，必须使得系统能够满足最恶劣条件下的通信。

发射天线高度仍为20 m，在加倍射线数基础上，再将接收距离加倍为200 km，电波到达高度与时延分布关系如图8所示。

由图4～6可知，波导高度相同，发射天线高度越接近波导高度，多径信号到达接收距离时同一接收高度上的径数越少，信号的最大多径时延(即图中接收高度上所有多径信号的时间跨度)越小，反之亦反。天线越低，射线跳数增加，多径情况越复杂，射线族越难分离。因此，分离多径信号族接收球法应用于天线高度极低情况时难度较大，此时可通过τmax粗略估计系统性能，好在一般舰船用通信天线高度不会低至贴近海面。

发射天线高度20 m，加倍射线数目，电波到达100 km处的高度与时延分布关系如图7所示。

图8 接收距离加倍时多径信号时延分布Fig.8 Distribution of multipath signal delay with receiving distance doubled

由图5和图8可知，径数和最大多径时延随距离增加而增大，但距离和最大多径时延增量不是直接的倍数关系。对于图8，根据式(12)可知接收球半径约为0.29 m。则16 m和20 m接收高度上，多径信号的相对功率G延迟剖面如图9和图10所示。

图7 射线数加倍时多径信号时延分布Fig.7 Distribution of multipath signal delay with ray number doubled

图9 16 m高度上相对功率延迟剖面Fig.9 Relative power delay profile at 16 m

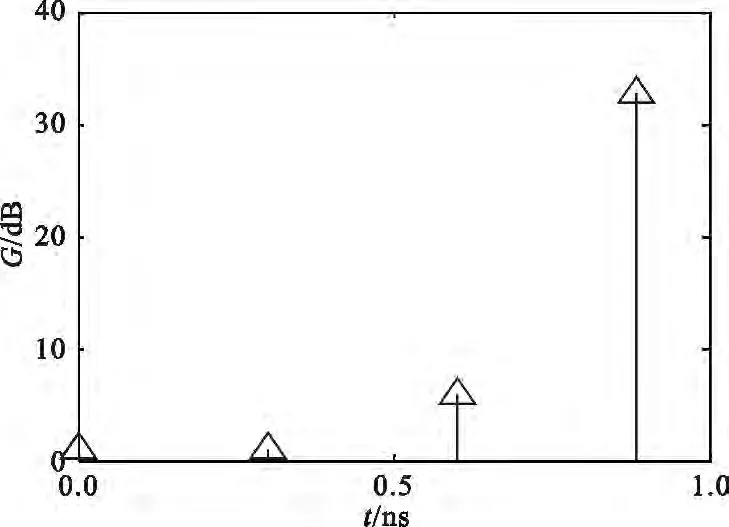
图10 20 m高度上相对功率延迟剖面Fig.10 Relative power delay profile at 20 m

由图9和图10可知，在16 m和20 m高度上，最大多径时延为0.885 ns，两种情况下主次径相对强度差可达26.8 dB，因此适当选择接收高度，可以使接收多径信号的相对强度达到最大，更加容易克服多径延迟对信号接收造成的影响，也可以用于指导自适应设计均衡器，实现更好的接收性能。

对于高度20 m上进行信号接收，取信号的符号周期 Ts为临界值，即0.885 ns，由式(16)可知系统相干带宽Δf为1.1 GHz。工程中通常采取冗余设计的办法降低信号处理的复杂度，不妨取符号周期为4、10倍的τmax以作对比，相应的通信带宽分别为280 MHz和110 MHz，则带限冲激响应如图11所示。

图11 带限冲激响应Fig.11 Bandwidth impulse response

因此，根据蒸发波导高度和预期的通信距离，基于SRT和海洋多径信号场强计算方法，仿真可得最大时延和功率延迟剖面，从而可得系统可用带宽和相应的带限冲激响应，根据辐射信号和带限冲激响应，评估系统的误码性能。当然，也可以据此自适应设计均衡器，进一步提高通信系统的误码性能。这对于基于软件无线电技术建立速率自适应数据通信，实现蒸发波导传输信道特性的高效利用具有重要指导意义。

4 结论

本文提出了一种基于RT进行蒸发波导通信中多径信号场强计算方法，给出了大气分层条件下SRT计算方法，综合考虑了电波空间扩散、粗糙海面反射和接收球法，计算电波到达强度，解决了大气波导内部多径信号强度难以计算的问题;研究了蒸发波导内部多径信号的特性;根据电波形成超视距传播条件和多径特性，研究了蒸发波导超视距通信系统设计使用策略;给出了基于多径特性建立带限冲激响应的方法，为蒸发波导通信的链路预算提供了有效的途径，通过控制路径损耗，维持正余量，达到期望的系统差错性能，也可以据此自适应设计均衡器，进一步提高通信系统的误码性能。仿真表明，一整套蒸发波导通信带限信道建模方法切实可行。蒸发波导通信前景诱人，适于波导高发区的岛屿、舰、岸之间移动通信节点的通信，数据速率和可通率较高，性价比优势明显。下一步将进行系统设计并开展试验验证。

[1]任香凝，李文计.海面蒸发波导微波超视距通信可行性分析[J].信息传输与接入技术，2008，34(2):22 －24.REN Xiangning，LI Wenji.Feasibility analysis on beyond－horizon microwave communication with evaporation duct over the sea[J].Radio Communications Technology，2008，34(2):22 －24.(in Chinese)

[2]Woods G S.High －capacity，long－ range，over ocean microwave link[J].IEEE Journal of Oceanic Engineering，2009，34(3):323 －330.

[3]吕英华.计算电磁学的数值方法[M].北京:清华大学出版社，2006:310 －315.LYU Yinghua.Numerical methods in computational electromagnetics[M].Beijing:Tsinghua University Press，2006:310 －315.(in Chinese)

[4]陈绍贺，郑辉，黄兴忠.大气波导中多径衰落信道参数的定量计算[J].电波科学学报，2010，25(4):638 －645.CHEN Shaohe，ZHENG Hui，HUANG Xingzhong.Numerical computation of parameters of multipath fading channel in the atmospheric duct[J].Chinese Journal of Radio Science，2010，25(4):638 －645.(in Chinese)

[5]赵楼，杨坤德，杨益新.海洋蒸发波导信道的多径时延[J].探测与控制学报2010，32(1):39 －44.ZHAO Lou，YANG Kunde，YANG Yixin.Multi－ path effect of Evaporation Duct[J].Journal of Detection ＆Control，2010，32(1):39 －44.(in Chinese)

[6]赵小龙，黄际英.大气波导中多径信道的参数研究[J].西安电子科技大学学报(自然科学版)，2008，35(2):314－318.ZHAO Xiaolong，HUANG Jiying.Research on multi －path channel parameters in the Marine atmospheric duc[J].Journal of Xidian University(Natural Science Edition)，2008，35(2):314 －318.(in Chinese)

[7]Sirkova I.Brief review on PE method application to propagation channel modeling in sea environment[J].Central European Journal of Engineering，2012，2(1):19 －38.

[8]Katherine L.A smart climatology of evaporation duct height and surface radar propagation in the INDIAN ocean[D].Monterey，CA:Naval Postgraduate School，2007.

[9]肖金光，周新力，刘晓娣.弯折谱估计在PE模型电波传播中的应用研究[J].电波科学学报，2014，29(3):559－566.XIAO Jinguang，ZHOU Xinli，LIU Xiaodi.Application of cured wave spectral estimation in wave propagation with parabolic equation model[J].Chinese Journal of Radio Science，2014，29(3):559 －566.(in Chinese)