载波频率号提取算法对箭载GLONASS速度计算的影响*

饶爱水，张 龙，王振平，汪 毅

(中国卫星海上测控部，江苏 江阴214431)

1 引言

GLONASS卫星采用频分多址的扩频信号，每颗卫星采用不同的载波频率而使用相同的测距码［1］，导航信号在不同的频率上播发使得接收机的设计更为复杂，也带来GLONASS测速的新特点。国内外关于导航系统测速的研究主要针对GPS测速，GLONASS测速以及“北斗”测速的相关文献较少。文献［2］研究了利用GPS单点测速技术测量海浪的运动速度，文献［3］研究了利用差分测速和Kalman滤波估计相位变率方法解算飞机飞行速度，文献［4］研究了利用自适应滤波方法减少影响GPS测速误差的方法，文献［5］分析了利用载波相位变率实时GPS测速的误差来源及其对测速的影响，文献［6］分析了多路径效应对实时动态精密单点定位的影响，文献［7］分析了多普勒对GPS测速的影响，文献［8］利用“北斗”实测多普勒观测量对其测速精度进行了初步探讨，文献［9］研究了箭载GLONASS单点定位的速度精度。本文研究GLONASS测速时载波频率号对高速运动目标测速的影响。

2 载波频率号参数介绍

GLONASS导航电文由一个超帧组成，每个超帧由5个帧组成，每个帧由15个串组成，含有24颗GLONASS卫星历书的全部内容，如图1所示。每个帧传送内容为GLONASS卫星的部分实时数据和给定的全部非实时数据。在帧结构上，第1～4帧相同，第5帧含有2个保留串。

L1载波和L2载波频率标称值(单位MHz)由如下表达式确定:

对于任何特定的GLONASS卫星，频道号K通过历书中的载波频率号HAn计算得到，2005年以后发射的GLONASS卫星的K取值为［－7，+6］。根据导航卫星测速原理，当接收机测得卫星信号多普勒频移fd后，可计算得出伪距变化率ρk为

式中，c为光速，fk为卫星的载波频率。联合公式(1)和公式(2)，可知频道号K的计算结果对GLONASS测速结果具有重要影响。

频道号K与历书参数载波频率号HAn之间的关系如公式(3)所示:

图1 GLONASS导航电文结构Fig．1 Navigation message structure of GLONASS

3 载波频率号算法设计及结果

根据GLONASS ICD文件规定，实时数据P3标识本帧内传送卫星历书的卫星数标志，“1”标识5颗卫星，“0”表示4颗卫星，P3位于每帧电文第3串的第80位，据此可以得出计算载波频率号的处理算法，本文称全帧积累算法，如图2所示。当电文串号m为7、9、11、13时，需要首先判断(m－1)串是否积累完毕，从中计算卫星号nA(位于第77～73位)，然后再从 m串中计算得到值，形成(nA、)配对表;当电文串号m为15时，首先要获取第3串中的P3值，为此需要积累本帧全部15串的数据，当P3值为1时再计算(nA、)的值。

保留串的存在，导致通过P3计算载波频率号的方法耗时较长，原因是需要积累一个完整的电文帧(共15串)才能确保P3值与第14、15串的值相匹配，至少需要积累30 s。该算法能获得正确的(nA、)配对表值，如表1所示。

图2 通过卫星数判断载波频率号Fig.2 Calculating carrier frequency number by satellite number

表1 卫星号与载波频率号配对表Table1 Counterpart table of satellite number and carrier frequency number

为了快速获得(卫星号、载波频率号)配对表，一种退化的算法是直接计算载波频率号，把第5帧的第14、15串数据当做正常数据处理，其算法流程如图3(a)所示，显然这种算法获得的载波频率号存在错误值;另一种保守的算法是丢弃第14、15串的数据(包括前4帧)，只处理第6～13串中的数据，其算法流程如图3(b)所示，根据GLONASS ICD文件说明，GLONASS历书在超帧内的排列如表2所示，这种方法将无法获取第5、10、15、20号卫星的载波频率号。

图3 错误的载波频率号计算算法Fig.3 Inaccurate calculation algorithm of carrier frequency number

表2 GONASS历书在超帧内的排列Table2 Arrangement of GLONASS almanac within superframe

通过观测保留的第14、15串的定义以及实际测量数据的分析，发现第15串的低数据位都为0，而非保留串的第15串的低数据位不为0，因此可以通过第15串的低位数据是否为0判断保留串，算法如图4所示。该算法与图2的算法类似，但由于无需积累完整一帧数据而具有较快的速度。

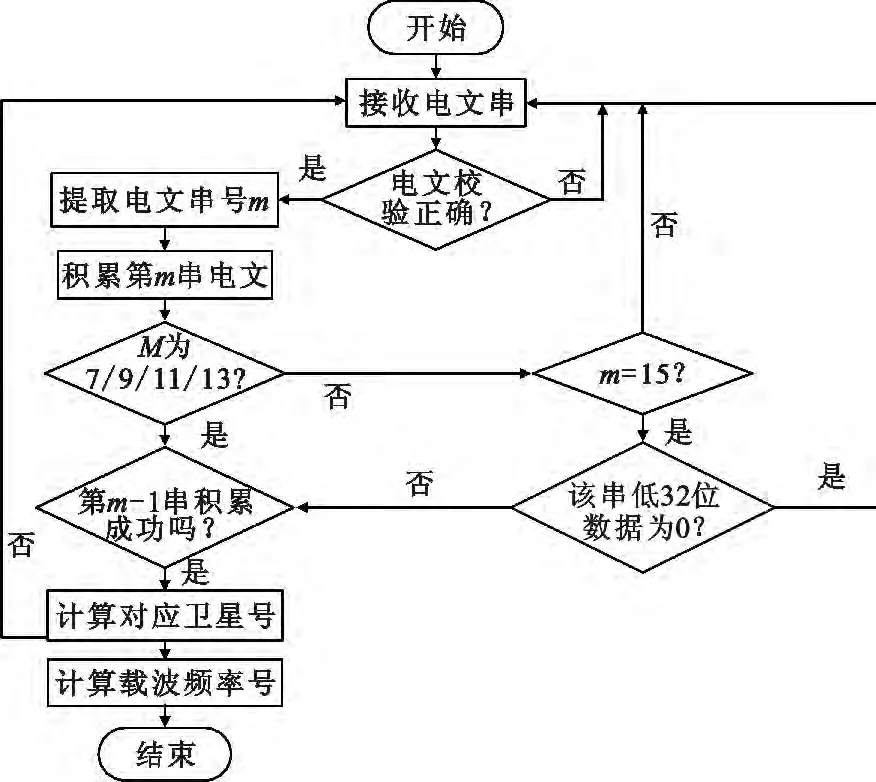
图4 通过保留位判断载波频率号Fig.4 Calculating carrier frequency number by reserve bits

通过复演某次火箭飞行任务数据，得出图2和图4两种算法计算载波频道号的时间曲线图，如图5所示。从图中可看出通过保留位判断载波频率号的算法可提前38 s计算出数据，对于短弧段实时测控任务，尽量缩短首次定位时间非常重要。

图5 两种载波频率号计算算法时间比较Fig.5 Time comparison between two carrier frequency number algorithms

4 载波频率号对速度精度的影响分析

4.1 速度误差理论分析

为考察载波频率号计算对速度精度的影响，公式(2)对fk进行微分，得到

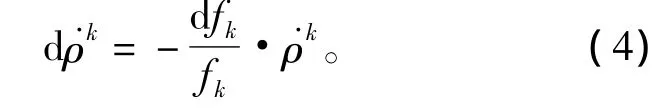
对于L1载波，fk近似取值为1602 MHz，dfk近似取值为(0.5625～0.5625×13)MHz， ρk近似为目标运行的速度V，可以估算得出

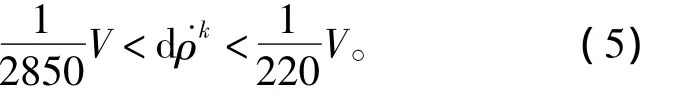
公式(5)即为载波频率号计算错误引起的速度误差值，对速度达几千米每秒的高速飞行器，最大可引起几十米每秒的误差，远超出试验任务要求的精度误差范围。

4.2 速度精度计算方法

采用伪距单点定位的最小二乘法，根据定位原理，有速度方程

式中，V为速度测量噪声向量，矩阵A为方向余弦矩阵，X为速度和钟差变化率向量，L为速度观测向量。根据最小二乘法的内符合精度估计公式，下面估算定位结果的精度[6]。

(1)伪距观测值的均方根差

式中，[vv]为残差V的平方和，n为观察到的卫星个数。

(2)未知数X的权逆矩阵Qxx

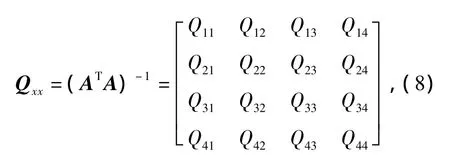
可得定位精度σP为

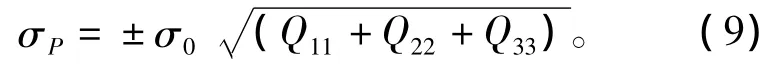
根据公式(9)，在定位计算时可一并获取到对应的速度精度。

4.3 实际计算结果

为估计载波频率号计算错误对速度精度的影响，在GNSS弹道计算软件中实现直接解算载波频率号算法(图3(a)算法)，通过复演某次火箭飞行试验数据，采用公式(9)估计GLONASS弹道精度，得到弹道精度曲线如图6所示。从图中可以看出引起的弹道精度误差在15～50 m/s之间，且精度误差随火箭运行速度增大而变大。分析该算法获取的8号卫星载波频率号有两个值，即6和0，0为获取到的错误值;该弧段内，火箭的飞行速度为7400～9400 m/s，根据公式(4)，dfk取值为(0.5625 ×6)MHz，可估算出由于载波频率号导致的速度精度误差最小值为15.6 m/s;根据公式(5)，可估算出速度精度误差最大值为42.9 m/s，理论分析与实际计算结果数据比较吻合。

图6 错误算法获取的GLONASS弹道速度精度曲线Fig.6 Curve of velocity precision of GLONASS trajectory calculated by inaccurate algorithm

采用图4通过保留位判断载波频率号的算法，估计该任务弧段GLONASS弹道精度，结果如图7所示。从图中可知，GLONASS弹道精度绝大部分在0.1 m/s以下，最大值在0.25 m/s左右，能够满足火箭飞行试验任务对速度精度计算的要求。

图7 正确算法获取的GLONASS弹道速度精度Fig.7 Curve of velocity precision of GLONASS trajectory calculated by accurate algorithm

5 结束语

随着导航系统的发展，GPS、GLONASS、“北斗”等导航系统用于测速服务的应用越来越普遍，不同导航系统对目标测速的影响因素多有不同。本文针对GLONASS测速问题，分析了载波频率号计算对测速的影响;在给出的4种载波频率号提取算法中，直接计算载波频率号算法获得错误的频率号，导致速度精度跳变，引起速度精度误差为目标飞行速度的1/2850～1/220;丢弃保留串算法无法获取第5、10、15、20号卫星的载波频率号，引起速度精度误差与直接计算载波频率号算法相同;通过卫星数判断载波频率号算法需要积累完整的电文帧，首次测速时间延长;而通过保留位判断载波频率号算法具有最小首次测速时间，缩短30 s以上。因此，通过保留位判断载波频率号算法具有最优的性能。

[1]刘基余.GLONASS现代化的启迪[J]﹒遥测遥控，2010，31(5):2 －6.LIU Jiyu.Some Enlightenment from GLONASS Modernization[J].Journal of Telemetry，Tracking and Command，2010，31(5):2 －6.(in Chinese)

[2]SHAN Rui，LIU Yanxiong，ZHAO Tiehu，et al.Research of the wave measurement using GPS absolute velocity estimation technology[J].Marine Science Bulletin，2013，15(2):59－70.

[3]田良辉，刘根友，郭爱智.Kalman滤波估计GPS载波相位变率的测速方法与实现[J].大地测量与地球动力学，2011，31(1):72 －77.TIAN Lianghui，LIU Genyou，GUO Aizhi.Method of Velocitymeasurement By GPS Carrier Phaserate Estimated From Kalman Filter and Its Implement[J].Journal of Geodesy and Geodynamics，2011，31(1):72 － 77.(in Chinese)

[4]仇立成，祝程程.自适应滤波在GPS测速中的应用[J].全球定位系统，2013，38(1):15 －17.QIU Licheng，ZHU Chengcheng.The Application of Adaptive Filter in Velocity Measurement with GPS [J].GNSS World of China，2013，38(1):15 －17.(in Chinese)

[5]郭爱智，王勇，刘根友，等.高频GPS实时单点测速误差分析[J].大地测量与地球动力学，2013，33(5):34 －38.GUO Aizhi，WANG Yong，LIU Genyou，et al.Error Analysis of High－Rate GPS Data Real Time Single－Point Velocity－Determination[J].Journal of Geodesy and Geodynamics，2013，33(5):34 －38.(in Chinese)

[6]万胜辉，杨遵龙，苏䶮.实时动态精密单点定位中的多路径效应削弱方法[J].电讯技术，2013，53(3):312 －317.WAN Shenghui，YANG Zunlong，SU Yan.Mitigation of Multipath Effects in Rear time Kinematic Precise Point Positioning[J].Telecommunication Engineering，2013，53(3):312 －317.(in Chinese)

[7]Zhang J.Short note:On the relativietic Doppler effect for precise velocity determination using GPS[J].Journal of Geodesy，2006，80(2):104 －110.

[8]王拓，吕志伟，殷实.“北斗”多普勒测速精度的分析[J].测绘信息与工程，2012，37(2):16 －19.WANG Tuo，LYU Zhiwei，YIN Shi，et al.Preliminary Accuracy Analysis on Velocity Determination Using COMPASS Doppler Measurements[J].Journal of Geomatics，2012，37(2):16 －19.(in Chinese)

[9]赵树强，许爱华，王家松，等.箭载GLONASS弹道确定及精度分析[J].宇航动力学学报，2012，2(2):27 －31.ZHAO Shuqiang，XU Aihua，WANG Jiasong，et al.Rocket Trajectory Determination and Precision Analysis Using On－ Board GLONASS Data Processing[J].Journal of Astrodynamics，2012，2(2):27 －31.(in Chinese)