基于指标重要度及代价的系统评价后续决策

段在鹏, 钱新明, 刘振翼, 黄　平, 夏登友,2, 多英全

(1. 北京理工大学爆炸科学与技术国家重点实验室, 北京 100081;

2. 中国人民武装警察部队学院消防指挥系, 河北 廊坊 065000;

3. 中国安全生产科学研究院, 北京 100012)



基于指标重要度及代价的系统评价后续决策

段在鹏1, 钱新明1, 刘振翼1, 黄平1, 夏登友1,2, 多英全3

(1. 北京理工大学爆炸科学与技术国家重点实验室, 北京 100081;

2. 中国人民武装警察部队学院消防指挥系, 河北 廊坊 065000;

3. 中国安全生产科学研究院, 北京 100012)

摘要：当系统某次评价不达标,选取怎样的方案使系统整改后达标便是评价后续决策问题。首先类比事故树基本事件重要度,建立能综合反映指标重要度的模型及改善代价的模型;之后对最大重要度所对应指标得分进行固定步长、渐升步长以及渐降步长等3种形式的增值,再求新的系统评价得分,直到系统评价满足阈值,并确定3种迭代模型的取舍策略;最后分析迭代过程及结果,建立指标改变先后度模型,确定指标改变的轻重缓急次序。文中以模糊综合评价方法为对象分析,实例验证切实可行,并可推广应用于灰色评价、可拓学评价以及集对分析等常规评价方法。

关键词：系统评价; 后续决策; 指标重要度; 改善代价; 改变顺序

Follow-up decision for system evaluation based on

0引言

模糊综合评价作为定性分析和定量分析综合集成的一种常用方法,已在工程技术、管理评价等方面得到广泛应用[1-3]。模糊综合评价应用的关键点其一是隶属函数的选取[4-5],其二便是指标权重的确定[6-7]。在以上工作基础上得到模糊综合评价结果,若其达标则评价结束,若不达标则会涉及后续决策问题,即通过改进层次结构中的某些指标内容,最终使系统整体评价达标的计划和措施。迄今基于模糊综合评价的后续决策研究主要局限于文字及章程方面,从系统计算角度进行后续决策问题的研究鲜有报道。从定量角度分析评价后续决策问题,最重要的是确定决策模型,而建模的根本目的是确定各指标得分变化的标准,即满足怎样的条件某些指标就可以增加得分,而剩余不达标的指标则只能保持得分不变,基于以上评价后续决策模型的算法也很重要,不同的算法其模型结果精度不同,计算效率也会有所差异,所以建立符合工程实际的后续决策模型和算法是评价后续决策定量分析的关键,也同样是其两个难点。故本文旨在从指标层各指标重要度角度研究模糊综合评价后续决策问题。关于重要度分析的研究较多,层次结构中的指标重要度常应用层次分析方法通过指标间相互比较确定[8-9];在此基础上,对于不同系统或研究对象的重要度分析,常应用贝叶斯网络[10]、神经网络[11]或蒙特卡罗模拟[12]等方法实现研究对象重要度研究;最后,基于故障树的基本事件重要度分析也是常用的重要度分析手段,且随着研究不断深入,故障树重要度分析已实现与模糊集[13]、粗糙集[14]以及二元决策[15]等理论的联用,不仅实现了理论间功能互补,也增加了其应用范围和可靠性。本文借助故障树中的基本事件重要度的概念进行类比分析层次结构中各指标层指标重要度,在此基础上找出最高重要度指标并对其修正得分,依此多次迭代直到最后系统评价得分达标，为基于模糊综合评价的后续决策研究提供一定理论基础。

1指标层重要度

1.1指标重要度模型

层次分析中的层次结构与故障树的树状外形存在相似性,故可以借鉴事故树3种基本事件重要度的本质来构造指标层各指标的重要度模型。利用事故树分析技术计算基本事件的重要度,主要是根据系统故障树中逻辑门的组合关系以计算出各基本事件对顶事件发生的影响程度,从而确定改进系统重点[16]。

基本事件的结构重要度IΦ(j),即不考虑基本事件发生的概率,仅从事故树结构上分析各基本事件的发生对顶上事件发生的影响程度;概率重要度Iq(j)=∂Q/∂qj,可表示第j个基本事件发生概率的变化而引起顶事件发生概率变化的程度,通过比率来表示这种变化;关键重要度Ic(j)=∂Q/∂qj/(Q/qj)=qjIq(j)/Q,反映了改变空间的概念,即一般情况下改变概率大的基本事件比改变概率小的基本事件容易[17]。

在以上事故树分析基本事件重要度分析的基础上,设某次评价共m个指标,得分集为(a1,a2,…,aj,…,am-1,am),则对任意第j个指标得分aj进行分析:

(1) 用指标权重表征结构空间,即某指标权重越高,则其越重要,其指标重要度越高,即指标权重正比于指标重要度,即

(1)

指标权重的确定,常细分为主观权重和客观权重两种思路,主观权重一般用层次分析法和Delphi法求取,而在数据资源充分的情况下常用熵权法和主成分分析法等求取客观权重。

(2) 用原始得分比率表征比率空间,参照故障树概率重要度构成。一般指标原始得分越高,其改变难度就越高,即指标的原始的分值与指标重要度成反比,即原始得分比率正比于指标重要度,即

(2)

(3) 仿信息熵公式表征改变空间:X向量含有N个元素,其中第i个元素xi比重为T(xi),则X向量信息熵为H(X)[18-19]：

(3)

信息熵公式表征信息含量,信息含量越高,则熵值越高,仿此,定义指标余度空间熵Sj

(4)

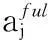
(5)

(4) 改变难易度:现实中有些指标虽然改变空间足够大,但是改变成本较高,相反,有些指标虽然Sj值较小,但却可以用相对小的成本进行改善。本文引进改变难易度ej以反映改变任意第j个指标时的改善代价,ej值越高,则表征改善代价越高,即改善该指标所需要的花费(消耗)则越大,则其指标重要度越低,即ej与指标重要度成反比，即

(6)

现就将改善代价表征的指标改变难易度e=(e1,e2,…,ej,…,em-1,em)分析如下:

若某次评价共m个指标,得分集为(a1,a2,…,aj,…,am-1,am),对第j指标得分aj进行分析:设第j指标保持得分aj状态稳定的成本为Qj,当得分aj变化,维持其稳定的成本Qj也随之变化,值得注意的是当aj增加,维持得分稳定的成本Qj可能增加,但也有不变甚至减小的可能。工程实际中,指标得分aj与成本Qj存在对应关系,通过确定多组不同(aj,Qj),最终便可拟合对应关系Qj=f(aj)。

维持得分aj的成本Qj除以得分aj本身,可称为成本率函数,或单位得分成本，即

(7)

qj表示第j指标得分为aj时,每单位分值所需成本,当第j指标得分为由aj-s变为aj-t,所需改善代价为

(8)

由式(8)可知,第j指标得分由aj-s变为aj-t所需改善代价为其单位成本qj在[aj-s,aj-t]的定积分,则总改善代价为

(9)

(10)

(11)

结合以上内容,将指标权重、原始得分比率、指标余度空间熵和改善代价等影响指标重要度的4个参数综合分析,得任意第j指标得分重要度模型

(12)

1.2模型算法

(1) 固定步长

(13)

在此步长下,任意第j∈(1,2,…,m)指标改善代价为

(14)

在此步长下,任意第j∈(1,2,…,m)指标改善代价为

(15)

在此步长下,任意第j∈(1,2,…,m)指标改善代价为

本文建议同时使用以上3种迭代计算,当三者迭代结果趋同时便将趋同结果作为最后结果;当两者趋同,一者不同时,则按两者趋同结果作为最后结果;当三者均不同,本文认为第3种先粗后细的迭代方式更有利于得到最佳结果,故将第3种迭代计算结果作为最后结果,值得注意的是,因为以上3种迭代计算结果均可满足迭代阈值条件,故使用单位也可按自身条件针对各指标情况酌情客观地选择,在此不再赘述。

1.3指标改善先后度

以上主要分析了求解最优得分向量的方法,当不达标厂家在经济预算紧张或系统运转困难时,不可能将以上不达标指标全部同时进行改善,选用如何的顺序方案可尽量使急需达改善的指标达标,而不甚急需指标则可适当放缓进行改善,以上为指标改变先后度的问题,本文认为,通过迭代计算,改善先后方案主要有3种选择,其一,当选重要度次数最多者;其二,分值改变最大者,其三,改善代价最低者,本文建立改变先后度模型,以综合反映三者作用。

(1) 指标当选频次率

假设第j指标在迭代过程中,共fj次当选为重要度最大者,则频次率系数Fj为

(16)

(2) 指标得分增率

第j指标的得分增率系数为

(17)

(3) 代价率

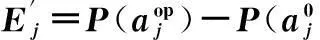
(18)

(4) 指标改变顺序判断度

综合以上分析,任意第j指标改变顺序判断度为

(19)

根据式(19)知,指标改变顺序判断度与得分增率的α次方及当选频次率的β次方成正比,而与代价率的γ次方成反比。指标K值越大,紧急性越高,改变次序越靠前。式(19)中参数α、β、γ分别表征了指标当选频次率、指标得分增率以及代价率等3个参量对判断度的整体影响。

1.4最优方案

综合以上分析可知,本评价后续决策模型的既知参数为初始得分,指标权重及指标成本,通过迭代计算,最终结果为最优迭代指标得分以及指标改变先后度,得出最优方案模型

(20)

式中，aop为最优得分序列;Kj∀j∈(1,2,…,m)为各指标的改变先后度；Gop为最优模糊综合评价得分；Gthr为预先设定的得分阈值。Gthr的计算将在下节阐述。

2模糊综合评价

2.1层次分析权重

设目标层A为单元素;准则层B包含p个元素;指标层C包含m个元素。对于同一层次上的元素建立一系列判断矩阵,以准则层之于目标层A-B为例，表1即其层次分析示意。

表1　A-B层次分析示意

(21)

2.2模糊综合评价

设因素集U=(u1,u2,…,um),评价集V=(v1,v2,…,vs)。通过隶属函数来实现数据模糊化,则V×U中的模糊关系设为R,其可用如下s×m阶矩阵表示,即

B=R·w

(22)

(23)

求得G之后,判断是否不小于预设阈值Gthr,即G≥Gthr,若满足则评价结束,若不满足则需要后续决策,即按第2.1节内容迭代寻优。总结以上内容,具体流程汇总如图1所示。

图1　模型迭代算法流程图

3算例分析

某化工园区采用热电冷联产(cogeneration of cooling, heating and power, CCHP)系统实现对园区企业的热、电、冷供应。因为联供系统在供热质量、节能、设备利用率、电网的安全性、环保等方面的优势,近年来已经成为化工园区公用工程岛的重要组成部分。但另一方面,联供系统因为涉及到整个园区的热电冷任务。建立一套能评选出多重指标综合最优的方案的评价指标体系尤其重要[20],文献[20]详细评述了冷、热、电三联供系统综合评价指标体系的建立及应用,结构简练且指标选取符合应用实际,故本文参照文献[20],建立该化工园区供三联供评价指标体系如图2所示。

图2　化工园区三联供评价指标体系

3.1层次分析权重

据图2,需首先分别对A-B、B1-C、B2-C、B3-C等各指标层次进行权重分析,因为B1-C、B3-C均为两元素,故直接赋值,故对A-B、B2-C分析如表2、表3所示。

表2　A-B层次分析权重

表3　B2-C层次A分析权重

C1、C2之于B1为两个元素,因本文的研究重点不在于层次分析法,故直接分别赋值为1/4和3/4;同理,赋值C6、C7之于B3的比重分别为3/7和4/7,故据式(21)得总权重:

即得权重:[0.096 9,0.290 6,0.065 5,0.028 6,0.075 0, 0.190,0.253 4]。

3.2模糊评价

选取5级保守梯形隶属度如图3所示,50~100分范围内打分,100~90分最优;80~90分次优;70~80分良好;60~70分次差;50~60分最差。隶属函数偏于保守:其一,在90~100分档,少去1线,即分数在此区间,其隶属度只有两个,该档评价值会相对较小,则最终评价分数不易进入该档次。50~60区间也少去1线,即少去1点,主要是考虑实际分数也可能在50分之下,此取法相当于平衡结果。评价集V=(50,65,75,85,95):前四区间取均值,最差区间取值50而非55,主要原因是打分范围为50~100,实际得分也可以取值小于50,为平衡结果故取50。本例取评价阈值Gthr=80,专家初次打分ast=[45,58,73,72,56,66,70],根据公式(22)、式(23),得综合评价得分Gst=64.126 0<80=Gthr,故需后续决策。

关于改变先后度方面,本文假设最看重改善代价,其次看中当选重要度频次,最不看重得分增率,则式(19)中各参数依次取为α=1、β=0.5、γ=4,由此构造各函数如图4所示。

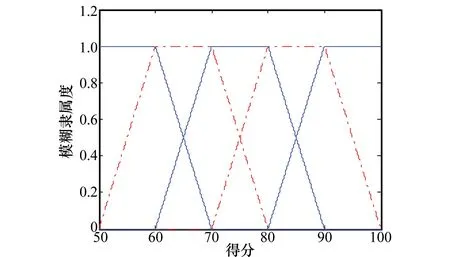
图3　梯形隶属度函数图

图4　指数函数图

3.3后续决策

设指标C1、C2、C3的“成本-得分”函数为Q1,2,3=-(a-60)2+5000;指标C4的“成本-得分”函数为Q4=175·a4;而指标C5、C6、C7的“成本-得分”函数未知,需要拟合确定,通过实践推算各得分、成本对应点(a,Q)分别为(0,0),(10,300),(20,500),(30,1 000),(40,1 500),(60,2 000),(70,4 000),(80,8 000),(90,10 000),(100,12 000),拟合确定“成本-得分”函数为Q5,6,7=0.011 8·a3-0.000 171·a2+6.6·a+176.0,则通过式(7)、式(8)可确定各指标单位成本及改善代价,如图5所示。

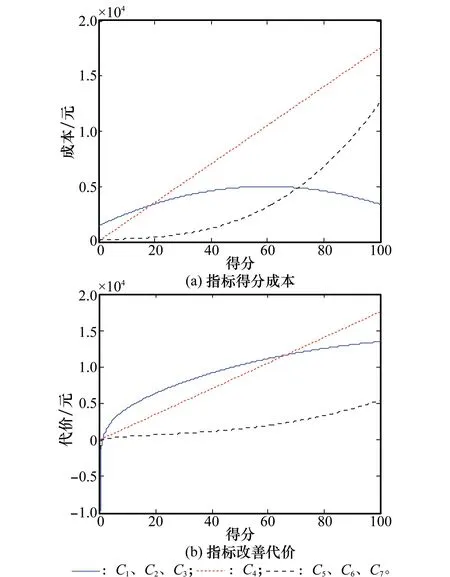
图5　指标成本及改善代价函数图

各指标成本,如图5(a)所示：

各指标单位成本：

各指标改善代价,如图5(b)所示：

本文设固定步长afix=0.01,步长因子φ=0.01,故“固定步长”、“渐升步长”和“渐降步长”分别按aj-step=0.01，aj-step=0.01×aj，aj-step=0.01×(100-aj)3种方法计算,将指标改变先后度、模糊评价迭代结果按以上3种步长计算方法汇总如图6~图8所示。

图6　固定步长时的指标改变先后度和模糊评价结果迭代

图6(a)中,指标C2和C1的得分率以及频次率分居第1、第2，但最终的改变率,指标C2虽然第1,但相较于C5并不明显,而C1仅排在了第5顺序改变,因为C2和C1的改善代价率偏高。

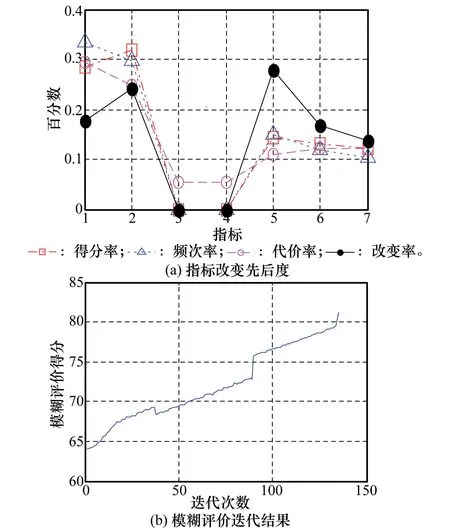
图7　渐升步长时的指标改变先后度和模糊评价结果迭代

图7(a)中,指标C2和C1的得分率以及频次率分居第1、第2,但最终的改变率,指标C5为第1,因为C5的代价率偏低。

图8　渐降步长时的指标改变先后度和模糊评价结果迭代

图8(a)中,指标C2的代价率虽然最高,但其得分率以及频次率也明显高于其他指标,故其居第一,通过该种步长迭代,改变指标较少,操作性增高。

指标重要度迭代结果及指标得分迭代结果按以上3种步长计算方法汇总如图9~图11所示。

图9　固定步长时的指标重要度和得分迭代图

图10　渐升步长时的指标重要度和得分迭代图

图11　渐降步长时的指标重要度和得分迭代图

通过图9~图11分析可知,3种步长模式下的指标得分及重要度变化趋于一致,分值不断变高,重要度不断变低,且指标得分有趋于各自稳定值的趋势,而指标重要度有逐渐趋于统一值的趋势。现就3种步长模式下的迭代计算结果汇总如表4~表6所示。

表4　后续决策固定步长迭代计算结果汇总表

表5　后续决策渐升步长迭代计算结果汇总表

表6　后续决策渐降步长迭代计算结果汇总表

综上分析:各指标初次得分ast=[45,58,73,72,56,66,70],系统得分阈值设为80分,经由固定步长827次迭代解算得最终评价得分为80.8043,优选得分aop=[68,88,73,72,66,78,81],各指标改变先后策略依次为C2:58→88;C5:56→66;C6:66→78;C7:70→81;C1:45→68;C3、C4不进行修正;总改善代价:6 250.6元;经由渐升步长135次迭代解算得最终评价得分为81.268 7,优选得分aop=[71,87,73,72,69,78,81],各指标改变先后策略依次为C5:56→69;C2:58→87;C1:45→71;C6:66→78;C7:70→81;C3、C4不进行修正;总改善代价:6 602.9元;经由渐升步长311次迭代解算得最终评价得分为80.019 3,优选得分aop=[45,97,73,72,56,76,81],各指标改变先后策略依次为C2:58→97;C7:70→81;C6:66→76;C1、C3、C4、C5不进行修正;总改善代价:3 903.4元。3种迭代方式中,渐升步长迭代步数最少,但其总改善代价最大;固定步长改善代价居中;渐降步长迭代步数居中,但改善代价明显降低,且修正指标偏少,可操作性增高。3种迭代方式的改变先后度结果均不一致,改变先后策略出现分歧,按照文中1.2节所述,最终取渐降步长的迭代结果。由图9~图11可知,3种步长模式下的指标得分及重要度变化趋于一致,分值不断变高,重要度不断变低,且指标得分有趋于各自稳定值的趋势,而指标重要度有逐渐趋于统一值的趋势。

4结论

(1) 建立了指标重要度模型

比照故障树基本事件重要度中的结构空间、比率空间、改变空间等概念,着重分析指标权重、原始得分比率、指标余度空间熵和指标改善代价等影响指标重要度的4个参量,建立了指标重要度模型。本文基于模糊综合评价的后续决策模型,但应用范围并不仅限于模糊综合评价。在既知初始得分,指标权重及指标得分成本等3个参量情况下,本模型亦适用于灰色评价、可拓学评价以及集对分析等常规评价方法。

(2) 提出了针对模型的迭代算法

提出基于固定步长、基于上步得分的渐升步长以及基于上步得分的渐降步长等3种迭代步长模型,并给出了针对以上3种迭代计算结果的取舍策略,即当三者迭代结果趋同时便将趋同结果作为最后结果,当两者趋同一者不同时,则按两者趋同结果作为最后结果,当三者均不同,则将“基于上步得分的渐降步长”的先粗后细的迭代结果作为最后结果。

(3) 提出了指标改变先后度模型

本文研究的最终结果为最优迭代指标得分以及指标改变先后度,最优迭代指标得分是一个参考值,即真实操作过程中的评价结果恰好为此值的几率非常小,但指标改变先后度却必须由本文提供的精确最优迭代指标得分求算,该模型主要综合反映了指标在迭代计算过程中当选重要度次数、得分改变值以及改善代价的混合作用。当厂家在经济预算紧张或系统运转困难时,可应用该模型确定指标改变的轻重缓急次序,有利于帮助厂家实现可靠而经济地达标。

参考文献：

[1] Chu W W, Li Y G, Liu C Q, et al. A manufacturing resource allocation method with knowledge-based fuzzy comprehensive evaluation for aircraft structural parts[J].InternationalJournalofProductionResearch, 2014, 52(11): 3239-3258.

[2] Liu L X, Liu Y, Shi G X. Study on the analytic hierarchy process and fuzzy comprehensive evaluation on the quality of teaching[J].JournalofChemicalandPharmaceuticalResearch, 2014, 6(2): 89-95.

[3] Du Z M, Wang J J. Analysis on highway landscape evaluation based on fuzzy comprehensive evaluation[J].JournalofHighwayandTransportationResearchandDevelopment, 2007, 24 (12): 14-18.

[4] Bhattacharyya B, Gupta, V K. Fuzzy based evolutionary algorithm for reactive power optimization with FAGS devices[J].IinternationalJournalofElectricalPower&EnergySystems, 2014, 21(61): 39-47.

[5] Lin C M, Li H Y. Adaptive dynamic sliding-mode fuzzy CMAC for voice coil motor using asymmetric gaussian membership function[J].IEEETrans.onIndustrialElectronics,2014,61(10):5662-5671.

[6] Sun Z Y, Zhang J Q, Zhang Q, et al. Integrated risk zoning of drought and waterlogging disasters based on fuzzy comprehensiveevaluation in Anhui province, China[J].NaturalHazards, 2014, 71(3): 1639-1657.

[7] Liu Y Q, Xu J P, Luo H W. An integrated approach to modelling the economy-society-ecology system in urbanization process[J].Sustainability, 2014, 6(4): 1946-1972.

[8] Kang J, Liang W, Zhang L B, et al. A new risk evaluation method for oil storage tank zones based on the theory of two types of hazards[J].JournalofLossPreventionintheProcessIndustries, 2013,29: 267-276.

[9] Zhong Y G, Xue K, Shi D Y. Assembly unit partitioning for hull structure in shipbuilding[J].Computer-aidedDesign, 2013, 45(12): 1630-1638.

[10] Lu Y J, Cheng B, Chen Y W, et al. Capability weightiness degree analysis of weaponry system-of-systems based on BN theory[J].SystemsEngineeringandElectronics, 2012, 34(8): 1605-1612.(鲁延京, 程贲, 陈英武, 等. 基于BN的武器装备体系能力重要度分析[J].系统工程与电子技术, 2012, 34(8): 1605-1612.)

[11] Dong Z Y, Dai K, Wang L. A neural network method for analyzing the units importance of system[J].ComputerScience, 2002,29(6):149-151.(董振亚,戴葵,王蕾.元部件重要度分析的一种神经网络方法[J].计算机科学,2002,29(6):149-151.)

[12] Wang B, Liu Q, Wang B, et al. Maintenance decision-making for EAF steelmaking system based on criticality[J].JournalofCentralSouthUniversity(ScienceandTechnology), 2013, 44(1): 14-24.(王宝, 刘青, 王彬, 等. 基于重要度的电弧炉炼钢系统维修决策[J].中南大学学报(自然科学版), 2013, 44(1): 14-24.)

[13] Liu P, Cheng X Q, Qin Y, et al. Sliding plug door system reliability analysis based on fuzzy fault tree[J].JournalofCentralSouthUniversity(ScienceandTechnology), 2013,44: 310-314.(刘萍,程晓卿,秦勇,等.基于模糊故障树的塞拉门系统可靠性分析[J].中南大学学报(自然科学版),2013,44:310-314.)

[14] Yang L J, Shen S M. Importance analysis of the fault tree based on rough set theory[J].JournalofNanjingUniversityofTechnology(NaturalScienceEdition),2007,29(1):60-64.(杨林娟,沈士明.基于粗糙集理论的故障树重要度分析[J].南京工业大学学报(自然科学版),2007,29(1):60-64.)

[15] Yu J, Sun L D, Shi Y L, et al. Analysis of fault tree importance of CNC machine tools based on BDD[J].MachineTool&Hydraulics,2008,36(12):186-189.(于捷,孙立大,石耀霖,等.基于BDD技术的数控机床故障树重要度分析[J].机床与液压,2008,36(12):186-189.)

[16] Purba J H. A fuzzy-based reliability approach to evaluate basic events of fault tree analysis for nuclear power plant probabilistic safety assessment[J].AnnalsofNuclearEnergy,2014,70(8):21-29.

[17] Wang F, Zhang J G, Liang X D, et al. Elevator safety risk and countermeasures based on FTA-TFN[J].AppliedMathematics&InformationSciences, 2014, 8(4): 1741-1748.

[18] Zhu Y G, Zhu Q J, Zhu Z W. Modeling, evaluation and analysis of tourism destination competitiveness: a case study of the Yangtze river delta of China[J].AsiaPacificJournalofTourismResearch, 2014, 19(8):932-949.

[19] Ji N N, Zhang J S, Zhang C X. A sparse-response deep belief network based on rate distortion theory[J].PatternRecognition, 2014, 47(9): 3179-3191.

[20] Cheng J F. Thermodynamic analysis and comprehensive evaluation of the combined cooling, heating and power cogeneration system[D]. Beijing: Beijing Construction Engineering College, 2010.(程建锋. 冷热电三联供的热力学分析与综合评价[D]. 北京: 北京建筑工程学院, 2010.)

段在鹏(1985-),男,博士研究生,主要研究方向系统安全分析、应急救援分析。

E-mail:duanzaipeng@163.com

E-mail:qsemon@bit.edu.cn

刘振翼(1975-),男,副教授,博士,主要研究方向为油气田开发与石油化工生产安全研究、危险物质安全性分析与检测技术。

E-mail:zhenyiliu@bit.edu.cn

黄平(1961-),男,副教授,博士,主要研究方向为含能材料与安全工程。

E-mail:ph6111@bit.edu.cn

夏登友(1973-),男,副教授,博士研究生,主要研究方向为应急救援指挥与技术。

E-mail:xiadengyou@126.com

多英全(1973-),男,高级工程师,博士,主要研究方向为危险化学品事故预防、安全分析、安全规划以及应急预案。

E-mail:duoyq@chinasafety.ac.cn

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150104.1331.006.html

index importance and costs

DUAN Zai-peng1, QIAN Xin-ming1, LIU Zhen-yi1, HUANG Ping1,

XIA Deng-you1,2, DUO Ying-quan3

(1.StateKeyLaboratoryofExplosionScienceandTechnology,BeijingInstituteofTechnology,

Beijing100081,China; 2.DepartmentofFireCommand,ChinesePeople’sArmed

PoliceForceAcademy,Langfang065000,China; 3.ChinaAcademyof

SafetyScienceandTechnology,Beijing100012,China)

Abstract:If any evaluation does not reach the standard, which plan should be selected to amend the system is the subsequent decision after evaluation. This article intends to study the subsequent decision for fuzzy comprehensive evaluation from the perspective of importance degree for indexes. Firstly, by comparing importance degrees of cases based on fault tree analysis, the model for importance degree of indexes representing index structure space, ratio space, modification space, and easiness for modification characteristics is built, meanwhile, models of score price, score unit price, and improvement costs are built. Then the importance degrees for indexes are calculated, and the score for the most important index is raised and the new evaluation score for the system is calculated. If the score does not satisfy the threshold, importance degrees for indexes are recalculated and previous steps are repeated, and iterative computation is performed till the system meets standard requirements. Three kinds of iterative models, i.e. fixed step, gradually ascending step and gradually descending step, are proposed, and trade-offs strategies for the three kinds of iterative models calculation results are given. Finally, the iteration process and results are analyzed; and the index modification priority model is established. When the budget is tight or the system is difficult to be operated, the model could be used to decide the priority for modifying indexes. The method is feasible by practical examples, and can be extended to the conventional evaluation methods such as the gray evaluation, extenics assessment and set pair analysis.

Keywords:system evaluation; follow-up decision; index importance; improvement costs; improvement priority

通讯作者钱新明(1967-),男,,教授,博士,主要研究方向为系统安全分析与安全评价技术、危险物质安全性分析与检测技术、应急救援分析与物资调运技术。

作者简介：

中图分类号：X 913

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2015.07.19

基金项目：“十二五”国家科技支撑计划(2012BAK13B01)资助课题

收稿日期：2014-08-15；修回日期：2014-11-12；网络优先出版日期：2015-01-04。