基于最优路径的弹道目标径向长度提取方法

黄　璟, 宁　超, 朱　勇

(北京环境特性研究所电磁散射重点实验室, 北京 100854)



基于最优路径的弹道目标径向长度提取方法

黄璟, 宁超, 朱勇

(北京环境特性研究所电磁散射重点实验室, 北京 100854)

摘要：针对强噪声环境中弹道目标径向长度提取困难的问题,提出了一种基于最优路径的弹道目标径向长度提取方法。首先对目标距离像进行时间积累,得到一维距离像时间序列,然后分别计算每相邻帧的距离像中各个像素之间转移的幅度代价函数和路径代价函数,根据总代价函数的大小判断各散射中心的相关性,搜索得到一条代价函数最小的路径即最优路径,确定目标头部和尾部散射中心的位置,进而得到各个时刻目标径向长度。该方法算法简单,在强噪声环境中也能保证较高的正确率。对仿真和模拟测试数据的分析处理验证了该方法的有效性。

关键词：宽带雷达;弹道目标;径向长度;最优路径

0引言

目标径向长度是指目标在雷达视线上的投影长度,是最直观的雷达特征之一,也是识别真假目标最直观的依据之一[1-8]。理论和实践已经证明,复杂目标在光学区的散射可以等效为若干散射中心的相干叠加,而一维距离像反映了散射中心在雷达视线方向上的分布特性[9],因此基于一维距离像提取径向长度就是找到径向上最远和最近的两个散射点并计算其距离。但是估计径向长度并不容易,其根本原因就是噪声对散射中心位置的提取影响很大。目前最为常用的径向长度提取方法就是采用门限检测法,但是该方法存在很多不足。首先是门限值与噪声是强相关的,这使得信噪比改变时门限值需要相应改变,否则就不能正确提取散射中心位置;其次是当信噪比较小时,噪声区域会出现超过门限的异常值,而排除这些异常值的难度非常大。这些不足使得门限检测法估计的径向长度往往误差较大,不能很好地应用于工程实际。为了克服门限法的不足,工程界提出了不少改进方法。文献[10-11]提出了一种基于自适应差分算子的径向长度提取方法,当信噪比大于15 dB时该方法能保证80%的径向长度提取平均正确率;文献[12]提出了一种快速傅里叶变换(fast Fourier transform, FFT)超分辨方法相结合的综合估计方法,该方法需要通过多重信号分类(multiple signal classification, MUSIC)方法提取散射中心,运算较为复杂,且需要高信噪比保证;文献[13]提出了基于图像边缘提取的径向长度提取算法,但是正确提取图像边缘又会遇到设置门限的困难。以上各种改进方法部分克服了门限法的缺点,提高了径向长度提取的正确率,但是仍旧没有解决在噪声环境特别是强噪声环境下的径向长度提取问题。

本文首先通过积累得到弹道目标距离像历程图,然后利用目标真实散射中心的连续性及虚假散射中心的不连续性,提出了提取散射中心的最优路径方法,基于该方法提取目标头尾散射中心,进而得到目标径向长度。该方法能够在各种信噪比环境下有效地提取弹道目标径向长度。仿真和模拟测试数据的分析结果表明了该方法的正确性,且计算简单,有利于实时处理。

1弹道目标的距离像历程图

假设宽带雷达带宽为B,回波数据经FFT变换后得到目标的一维距离像序列为SN,其中距离像点数为N,如果将SN经过积累,则得到距离像矩阵HN×M,距离像帧数为M,其中每帧距离像已经过对准处理。经此处理得到的距离像矩阵HN×M亦称距离像历程图。显然,该距离像矩阵的行表示雷达获得每一帧距离像的时刻编号,矩阵的列表示距离像的径向距离,该矩阵能够较为形象地表征目标距离像随时间的变化过程。由于宽带雷达的成像窗口一般达到百米量级,而弹道目标径向长度一般不超过10m,故在实际应用中,成像后仅需选取径向距离为十米量级的窗口范围,以减小计算量。

弹道目标的基本外形可分为平底锥、球体锥、平底锥柱头体和球体锥柱头体等[9]。在光学区,这些目标基本外形的头部和尾部皆存在较强的散射中心[9]。另一方面,由于弹道中段目标飞行姿态不会发生较大的突变,故散射中心在雷达视线上也不会发生大的突变。从距离像历程图上看,即图像的峰值位置不会发生大的突变,是连续的。而虚假散射中心是由噪声引起的,其在距离像历程图中的峰值位置是突变的,不连续的。这一特点在单帧距离像中体现不出来,而在距离像历程图中则可以明确地体现,这也正是最优路径法的物理本质。图1(a)为某时刻单帧距离像,在单帧距离像上出现了噪声引起的较强峰值。噪声引起的强峰幅度甚至高于了实际目标尾部散射中心。图1(b)为仿真的典型弹道目标在信噪比0dB时的中段距离像历程图,设定仿真条件为:雷达工作在C波段,目标存在进动周期5s,进动角5°的微动,采样频率10Hz。要从此单帧距离像正确提取目标径向长度难度极大,但从距离像历程图上看,目标真实散射中心变化依旧是比较明显的。

2基于最优路径的径向长度提取

由图1(a)可见,在噪声环境下弹道目标距离像的峰值点并不一定是目标真实散射中心,而且噪声峰值点幅度甚至有可能比目标真实散射中心峰值点高。但是由图1(b)可见,由于噪声引起的峰值点是随机变化的,故从距离像历程图上看,噪声引起的虚假峰值点不能形成连续过程,而由实际目标散射中心引起的峰值是比较连续地变化的,最优路径法就是基于这个前提进行的。

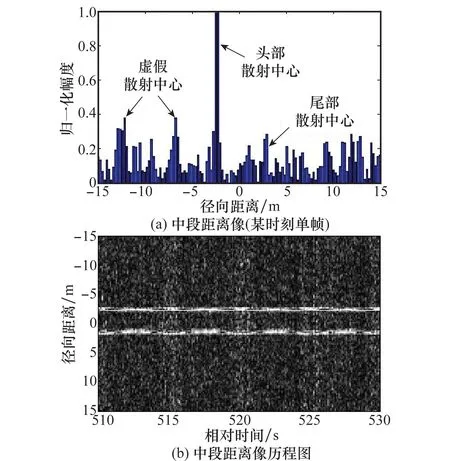
图1　典型弹道目标中段距离像及历程图

考虑一个待处理的距离像历程图矩阵HN×M,N为每帧距离像点数,M为距离像帧数。首先考虑只提取一个散射中心的情况:假设提取的第1帧距离像散射中心位置为N1,第2帧散射中心位置为N2,第M帧散射中心位置为NM。则提取的散射中心位置构成了一个序列P

(1)

由于该序列中的元素为对应距离像帧中的元素位置,故该序列称为散射中心的路径。显然,这个路径存在NM种可能,令这个可能的集合为K,则定义最佳路径[14-16]为

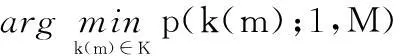
(2)

式中，g(k(m),k(m+1))和f(H(k(m),m))分别为路径代价函数和幅度代价函数；p(k(m);1,M)为从第1帧到第M帧距离像所有可能路径下的总代价函数,最佳路径即为使得总代价函数最小的路径。代价函数由g(k(m),k(m+1))两部分组成。

路径代价函数表征了从第m帧某个元素到第m+1帧某个元素的路径代价。根据之前的分析,如果这两个元素之间相差越大,则路径代价越大。可定义该函数[17-18]为

(3)

式中,c和Δ为路径代价函数的参数,c为斜率参数,Δ为门限参数。值得指出的是,路径代价函数的形式和参数都是开放的,对于不同的工程问题以及使用条件,可以选择不同的函数形式。但总的原则就是相邻帧两个元素间隔越大,其路径代价将越大。

f(H(k(m),m))为幅度代价函数。f()表示对每一帧距离像的幅度按降序排序后的序号数据。设X=[x1,x2,…,xN]为某一帧距离像的幅度,则

(4)

式中，sn表示为xn的降序排序序号。显然,若xn=max(X),则sn=1,若xn=min(X),则sn=N。根据以上定义,幅度代价函数值域范围为[1,N],且距离像幅度越大,幅度代价函数越小。

根据最佳路径的代价函数可见,最佳路径考虑了距离像历程图中峰值点的幅度和位置两个因素,能够满足最佳路径的峰值点序列必然是具有一定幅度且位置不发生突变的,这即符合距离像历程图中目标真实散射中心的特点。

如果直接根据最优路径的公式进行计算,计算量是非常巨大的。在实际使用中,一般采用分步循环法进行计算。在开始计算前,首先定义一个局部代价函数π

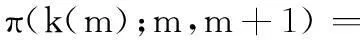
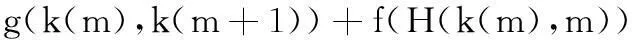
(5)

该代价函数仅反映从第m帧到第m+1帧的路径转移代价,且不包含当前帧的幅度代价。

计算开始后,首先计算H(1∶N,1)→H(1,2)的局部代价函数:

(6)

显然,k(1)=1,2,…，N,π(k(1);1,2)为一个长度为N的代价序列。则令

(7)

为更新后的H(1,2)元素的幅度代价,按同样的方法计算H(1∶N,2)更新后的幅度代价。完成H(1∶N,2)所有幅度代价的更新后,再依次计算H(1∶N,3),直到第H(1∶N,M-1)完成幅度代价的更新。

然后计算H(1∶N,M-1)→H(1∶N,M)的总转移代价。此时计算总转移代价仅需在更新后的H(1∶N,M-1)幅度代价基础上加上H(1∶N,M-1)→H(1∶N,M)的路径代价函数即可。

能使总转移代价最小的路径即为H(1∶N,M-1)→H(1∶N,M)的最优路径。最后依次往前递推,得到

各个步骤下的最优路径。综合得到的各单步最优路径,即得到H(1∶N,1)→H(1∶N,M)的最优路径。

图2即为一个H4×3距离像矩阵的处理过程实例,其中设定路径代价函数参数Δ=1,c=2.5。图2中的元素已经为降序处理后的顺序序号。

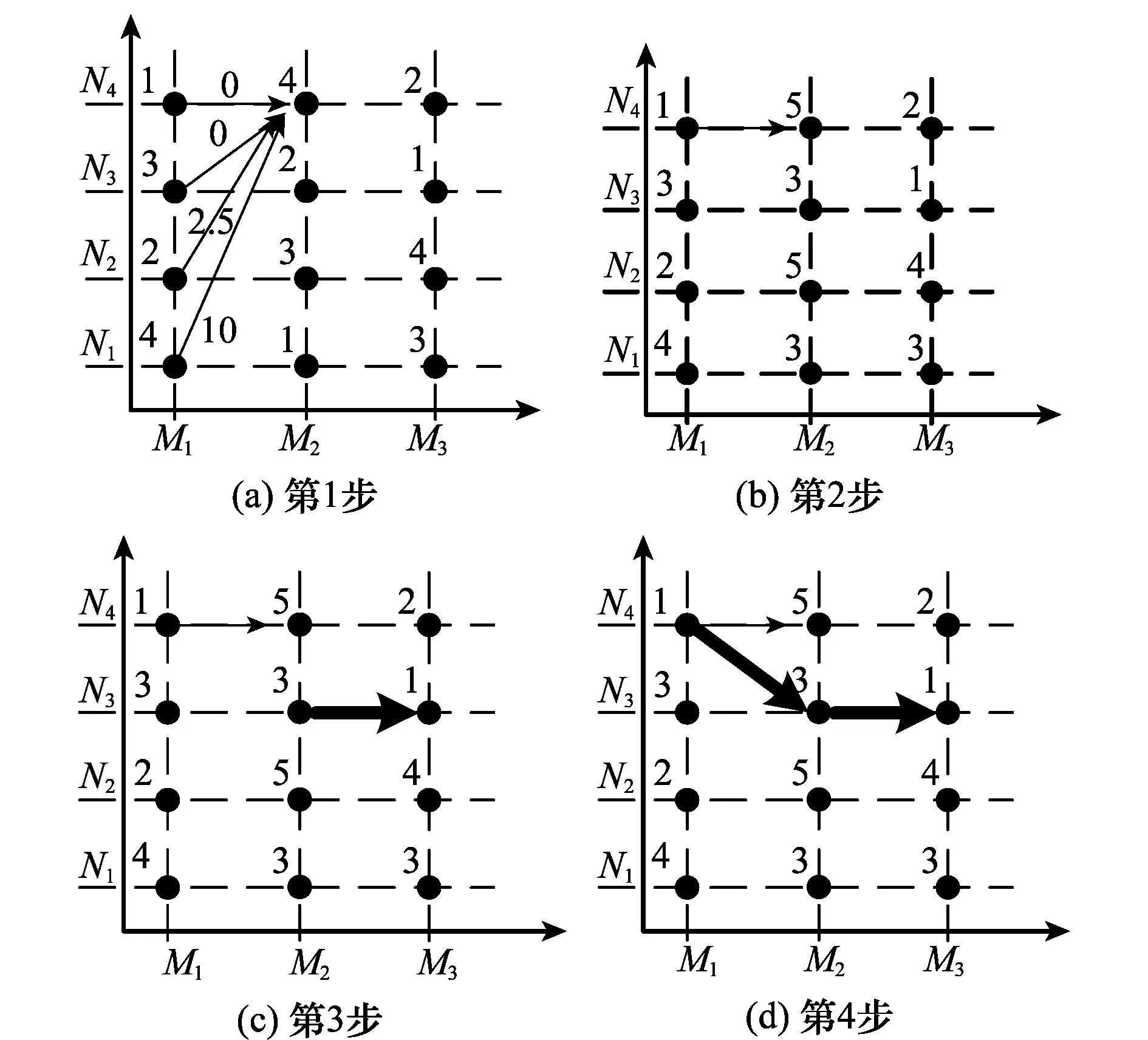
图2　最优路径法处理过程

图2(a)即为H(1∶4,1)→H(1,2)的局部代价函数计算过程,H(1∶4,2)更新后的幅度代价如图2(b)所示。图2(c)中的黑色加粗箭头为H(1∶4,2)→H(1∶4,3)的最优路径,图2(d)中的黑色加粗箭头为最后得到的最优路径。根据最优路径,即可得到本例距离像散射中心位置为[N4,N3,N3]。

对于弹道目标径向长度提取问题,需要从距离像历程图中提取头尾两个散射中心才能得到径向长度。相较于其他复杂目标,弹道目标的外形较为简单,其散射中心主要集中在目标头尾。假设FFT成像的主瓣宽度为W点,在基于最优路径法提取一个散射中心位置后,则令提取散射中心位置±W/2点的距离像幅度为0,然后再进行一次基于最优路径的散射中心提取,即能获得第二个散射中心位置序列。最后根据雷达带宽、成像点数及两个散射中心位置间隔即可得到目标径向长度估计。如果弹道目标的头尾散射中心在径向上十分接近以致成像后无法分开,则径向长度即为零。

基于最优路径的弹道目标径向长度提取方法总结如下:

步骤 1获得弹道目标距离像历程图矩阵,依次计算每帧距离像更新后的幅度代价;

步骤 2根据更新后的幅度代价,从最后一帧开始计算前一帧到当前帧的总转移代价,得到前一帧到当前帧的最优路径;

步骤 3综合各单帧间的最优路径,得到总的最优路径;

步骤 4根据FFT主瓣宽度,将提取的第一个散射中心位置及附近位置的距离像幅度置0,再从步骤1开始提取第二个散射中心;

步骤 5根据提取的两个散射中心位置及雷达参数,估计目标径向长度。

3基于仿真和模拟测试的分析

为了验证基于最优路径提取弹道目标径向长度地有效性,根据弹道理论建立了中段飞行弹道,并设定目标进动周期5 s,进动角5°,雷达为C波段,带宽600 MHz,成像间隔0.1 s,结合暗室实测典型弹道目标电磁散射数据得到仿真的目标距离像历程图。设定路径代价函数参数Δ=1,c=2.5。在信噪比分别为10 dB和0 dB两种情况下提取的径向长度如图3所示。

图3　最优路径法提取得到的径向长度结果

由图3可见,在信噪比分别为10 dB和0 dB的情况下,基于最优路径所提取的目标径向长度和理论径向长度十分接近。在相同信噪比下,基于门限法得到的径向长度如图4所示,首先将距离像幅度进行归一化,设定提取门限为0.2。由图4可见,当信噪比为10 dB时,门限法提取的径向长度已经出现较大偏差,而当信噪比为0 dB时,门限法已经完全失效。

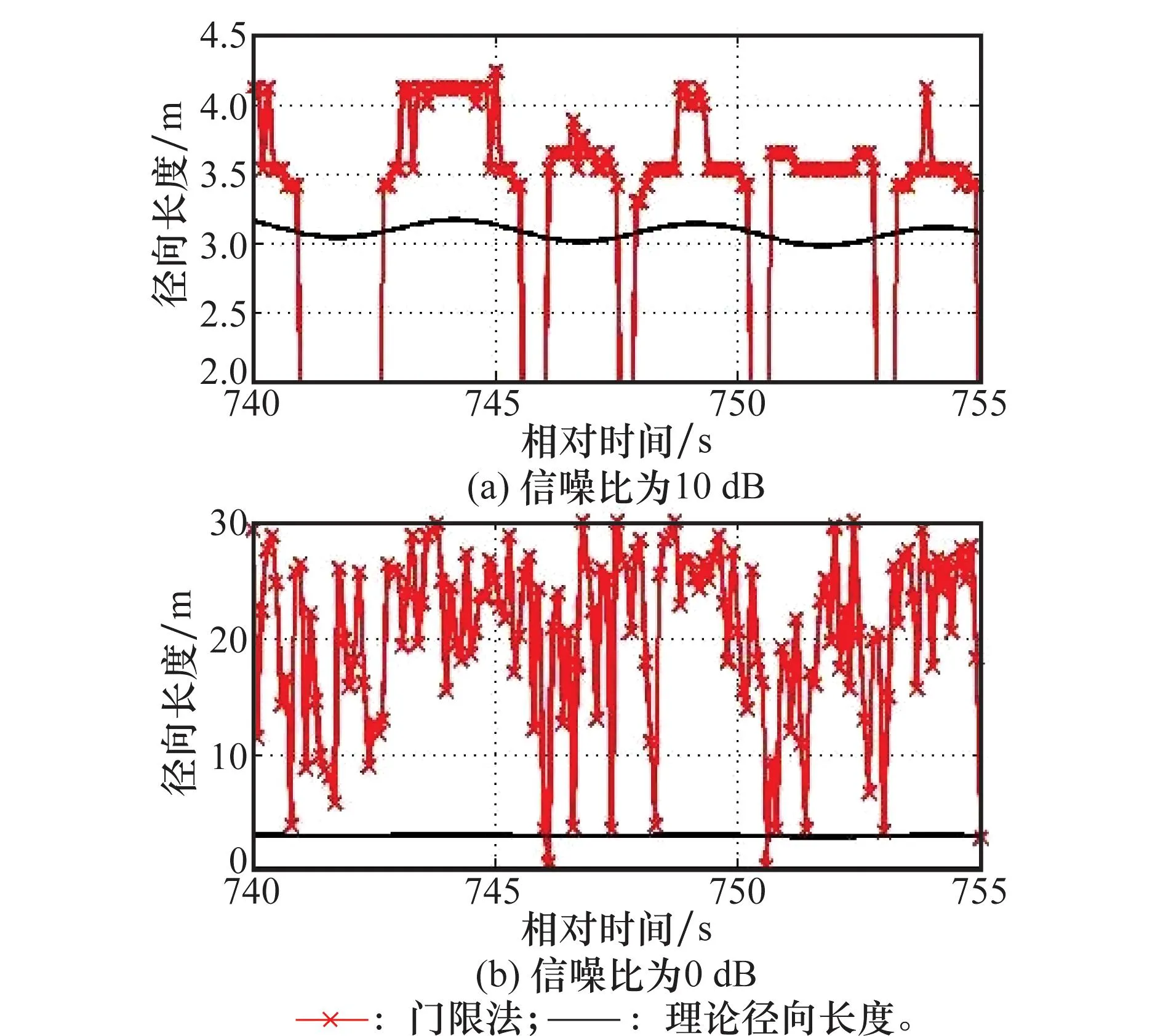
图4　门限法提取得到的径向长度结果

图5是暗室实测Ku波段典型弹头微动模型的距离像历程图。设定该典型弹头微动模型进动周期为10 s,设置信噪比为0 dB。图6为基于最优路径方法提取的目标径向长度。由图6可见,在强噪声环境中,基于最优路径方法提取的目标径向长度是正确的,而且实验结果正确反映了目标微动所引起的径向长度周期性变化。

图5　暗室实测典型弹头微动模型的距离像历程图

图6　提取的目标径向长度

4结论

本文针对强噪声环境中弹道目标径向长度提取困难的问题,提出了一种基于最优路径的弹道目标径向长度提取方法。该方法能够适应信噪比大范围变化,可以有效提高在强噪声环境中弹道目标径向长度提取正确率。该方法计算简单,有利于实时处理。通过对仿真和模拟测试数据的分析验证了该方法的有效性。

参考文献：

[1] Xu R C, Jiang W D, Chen Z P. Study of method of range profile feature extraction[J].SystemsEngineeringandElectronics, 2005, 27 (7): 1173-1174.(许人灿,姜卫东,陈曾平. 目标一维距离像特征提取方法研究[J].系统工程与电子技术,2005, 27(7): 1173-1174.)

[2] Huo K, Deng B, Liu Y X, et al. High resolution range profile analysis based on multicarrier phase-coded waveforms of OFDM radar[J].JournalofSystemsEngineeringandElectronics, 2011, 22(3): 421-427.

[3] Zhang X F, Wang P H, Du L, et al. New method for radar HRRP recognition and rejection based on weighted majority voting combination of multiple classifiers[C]∥Proc.oftheIEEEInternationalConferenceonSignalProcessing,CommunicationsandComputing, 2011:1-4.

[4] Li M S, Yan Z M. An algorithm based on HRRP for target re-cognition[C]∥Proc.oftheInternationalConferenceonImageAnalysisandSignalProcessing, 2012:71-73.

[5] Hou Q Y, Chen F, Liu H W, et al. New statistical model for radar HRRP target recognition[J].JournalofSystemsEngineeringandElectronics, 2010, 21(2): 204-210.

[6] Guo Z H, Li S H. One-dimensional frequency-domain features for aircraft recognition from radar range profiles[J].IEEETrans.onAerospaceandElectronicSystems, 2010, 46 (4): 1880-1892.

[7] Fu J S, Liao K, Yang W L. Synthetical generalized discriminate analysis for radar HRRP target recognition[C]∥Proc.oftheInternationalConferenceonInformationScienceandEngineering, 2010: 4106-4109.

[8] He S S, Zhou J X, Zhao H Z, et al. Estimating the precession angle of ballistic targets in midcourse based on HRRP sequence[C]∥Proc.oftheIEEERadarConference, 2008:1006-1009.

[9] Huang K P,Yin H C,Xu X J.RadarTargetcharacteristics[M]. Beijing: Publishing House of Electronics Industry, 2004: 86-98.(黄培康,殷红成,许小剑. 雷达目标特性[M].北京:电子工业出版社,2004: 86-98.)

[10] Liao K. Study of radar automatic target recognition base on high range resolution profile[D]. Chengdu:University of Electronic Science and Technology of China，2012: 24-30.(廖阔. 基于高分辨距离像的雷达自动目标识别研究[D].成都:电子科技大学,2012: 24-30.)

[11] Liao K, Gui G, Chen Z X, et al. High resolution range profile based extraction of radar target length[J].InternationalJournalofthePhysicalSciences, 2011, 6(23): 5503-5510.

[12] Jin G H. Research on ISAR imaging and physical feature extraction of midcourse ballistictarget[D]. Changsha:National University of Defense Technology, 2009: 67-75.(金光虎. 中段弹道目标ISAR成像及物理特性反演技术研究[D].长沙：国防科学技术大学,2009: 67-75.)

[13] Huo C Y, Huang J, Ren H M. Analysis method of wide-band feature by the procedural image of scattering centers[J].JournalofAntennas, 2010: 275-277.(霍超颖,黄璟,任红梅.基于散射中心历程图的宽带特征分析方法[J].天线学报,2010: 275-277.)

[14] Igor D, LJubisa S. An algorithm for the Wigner distribution based instantaneous frequency estimation in a high noise environment[J].SignalProcessing, 2004, 84(3): 631-643.

[15] Thayaparan T, Stankovic L, Djurovic I. Micro-Doppler-based target detection and feature extraction in indoor and outdoor environments[J].JournaloftheFranklinInstitute,2008, 345(6): 700-722.

[16] Guan Y S, Liu H W, Chen F. Micro-motion targets resolution in a high noise environment[C]∥Proc.oftheInstituteofEngineeringTechnologyInternationalRadarConference, 2009: 2630-2635.

[17] Rakovi′c P, Dakovi′c M, Thayananthan T. An algorithm for detecting a maneuvering target based on TFR and viterbi algorithm[C]∥Proc.oftheInternationalWorkshoponSymbolicandNumericalMethods,ModelingandApplicationstoCircuitDesign, 2010:1-4.

[18] You Q M, Li Y H, Rahman M S, et al. A near optimal routing scheme for multi-hop relay networks based on viterbi algorithm[C]∥Proc.oftheIEEEConferenceonWirelessCommunicationsSymposium, 2012:4531-4536.

黄璟(1983-),男,工程师,硕士,主要研究方向为雷达信号处理、目标识别。

E-mail:skytreehj@163.com

宁超(1978-),男,高工,博士,主要研究方向为雷达特征提取、目标识别。

E-mail:nc_09@sina.com

朱勇(1976-),男,研究员,硕士,主要研究方向为雷达系统、目标特性。

E-mail:happy_zhy@sina.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150312.1640.001.html

Estimation method for ballistic target range profile length

based on the optimal route algorithm

HUANG Jing, NING Chao, ZHU Yong

(ScienceandTechnologyonElectromagneticScatteringLaboratory,Beijing

InstituteofEnvironmentalFeatures,Beijing100854,China)

Abstract:In order to estimate the ballistic target range profile length under the high noise condition, a new method is proposed based on the optimal route algorithm. Firstly, integrate the high resolution range profile (HRRP) series for a period, then calculate values of cost functions on amplitude and distance when a pixel in this HRRP transfers to another in the next HRRP. By comparing total costs of the transfer, the relativity of strong scatter centers can be confirmed. An optimal route is found on which the values of cost functions are minimal. Then the position sequence of the strong scattering centers on the target is obtained. The HRRP lengths of the target can be estimated for the period by calculating the distances between its head and bottom. The method is simple in arithmetic processing and can improve the correctness for range profile length estimation in a high noise background. The effectiveness of the proposed method has been verified by analyzing simulation data and experimental data.

Keywords:wideband radar; ballistic target; range profile length; optimal route algorithm

作者简介：

中图分类号：TN 957.51

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2015.07.06

收稿日期：2013-04-16；修回日期：2014-11-06；网络优先出版日期：2015-03-12。