一种基于同态滤波器与Radon变换的光照不变人脸识别方法*
一种基于同态滤波器与Radon变换的光照不变人脸识别方法*
通信地址:730070 甘肃省兰州市西北师范大学计算机科学与工程学院Address:College of Computer Science and Engineering,Northwest Normal University,Lanzhou 730070,Gansu,P.R.China
齐永锋1,火元莲2
(1.西北师范大学计算机科学与工程学院,甘肃 兰州 730070;
2.西北师范大学物理与电子工程学院,甘肃 兰州 730070)
摘要:为了减轻光照变化对人脸识别精度的影响,提出了一种结合同态滤波器与Radon变换的人脸识别方法。首先用高斯同态滤波器对人脸图像进行处理,然后进行Radon变换,将变换得到的Radon特征用2DPCA/2DLDA进行降维。在Yale和PIE人脸数据库上的实验结果表明,提出的方法在光照变化较大时,其识别精度远高于2DPCA和2DLDA,是一种高精度的人脸识别算法。
关键词:同态滤波器;Radon变换;人脸识别
1引言
由于在公共安全、身份认证和视频监控等领域的应用前景,近年来,人脸识别一直是模式识别领域的研究热点[1~3]。在人脸识别任务中,特征提取是最为关键的步骤,但由于人脸是非刚性的,光照、姿态、表情等因素大大地影响了提取特征的稳定性。“同一个人的人脸图像在不同光照条件下提取特征的差异甚至大于相同光照条件下不同人的人脸图像间的差异”[4]。因此,减轻光照变化对人脸特征稳定性的影响在人脸识别任务中具有重要的意义。
为了减轻光照变化对提取特征的影响,研究者提出了许多方法。这些方法可归纳为图像预处理、3D光照模型和光照不变特征提取三种方法[5~7]。在第一类方法中,通过图像预处理技巧,将不同光照条件下的人脸图像变换到同一光照条件下,然后提取人脸特征。这些方法主要包括直方图、Gamma矫正等。3D光照模型需要不同光照的人脸图像构建一个表示光照变化的低维子空间,其计算量较大。光照不变特征提取方法的主要目的是提取人脸图像不随光照而改变的那些特征,主要有基于Gabor、LBP、LDP等方法,这些方法提取的特征不随光照变化而发生显著的改变。
研究表明,同态滤波器在处理图像光照不均方面具有良好的效果[8]。通过减少低频成分并增加高频成分,同态滤波器能够减少光照变化并锐化边缘或图像的细节,是一种增强图像对比度和压缩图像亮度范围的特殊滤波方法[9]。因此,用同态滤波器对光照不稳定人脸图像进行处理,可减轻同一个人的人脸图像在不同光照条件下提取的特征的差异。
在人脸识别任务中,除了光照因素引起人脸特征的不稳定外,成像角度、成像距离以及人脸的旋转也是导致人脸特征不稳定的重要因素,因此,降低这些因素的影响在人脸识别任务中也具有重要的意义。Radon变换[10]具有很好的抗噪性能,其提取的特征对图像平移、旋转和缩放等几何变换具有不敏感性,可用来提取人脸的几何变换不变特征。
为了提取光照不变与几何变换不变的人脸特征,本文结合同态滤波器和Radon变换,提出了一种新的人脸特征提取方法。首先将人脸图像经过Gamma变换,调整人脸图像的灰度范围,然后采用同态滤波器,降低低频成分和增强人脸图像的高频成分,使得被部分阴影遮挡的人脸细节部分更好地显示出来;接着采用Radon变换对人脸图像进行变换,以便得到能够对噪声污染不敏感的人脸图像旋转、缩放不变特征;最后采用二维降维方法降低提取的人脸图像的特征维数并进行识别。
2同态滤波器对人脸图像光照不均的处理
灰度图像f(x,y)可表示为入射分量与反射分量的乘积,假定入射分量为i(x,y),反射分量为r(x,y),则:
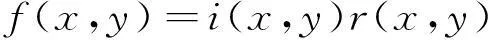
(1)
其中,入射分量0 Figure 1Face image pre-processing 在图1中,f(x,y)表示待处理的原始图像,Ln代表对数运算,DFT代表傅里叶变换,IDFT代表傅里叶逆变换,Exp表示指数运算,g(x,y)表示经过滤波后的图像。 由于关系到抑制低频分量同时增强高频分量,所以同态滤波器的选择很重要。本文选择高斯型同态滤波器进行滤波,其滤波函数如下: (2) 其中,γH表示高频增益,γL表示低频增益,D(u,v)表示频率(u,v)到滤波器中心的距离,D0表示截止频率。当γH>1,γL<1时,滤波器增强高频成分,减弱低频成分。但是,对于γH和γL的具体选择,并没有明确的理论公式可用,通常是通过反复实验得到比较合适的值。 本文在处理人脸图像光照变化时,首先对人脸图像进行Gamma校正,然后用高斯同态滤波器进行处理。图2和图3分别给出了原始人脸图像与经过光照处理后的人脸图像的对比,从图中能够看到,经过光照处理后,原始人脸图像中的光照不均现象得到了较好的矫正。 Figure 2 Origin image图2 原始图像 Figure 3 Light-corrected image图3 光照矫正后图像 3人脸图像的Radon变换 人脸图像f(x,y)的Radon变换是指f(x,y)沿平面内不同的直线做线积分,其数学表达式为: (xcosθ+ysinθ))dxdy (3) 由上式可知道,图像f(x,y)的Radon变换实际上就是沿直线r-(xcosθ+ysinθ)的积分。其中,r表示坐标原点到积分直线的距离,θ表示直线与坐标轴的夹角。 假定人脸图像遭到零均值白噪声污染,那么图像可表示为: (4) 其中η(x,y)为噪声,由于Radon变换是图像的线积分,在连续情况下,在所有的点和方向上,噪声的Radon变换是不变的,等于噪声的均值。即: (5) 由式(5)可知,人脸图像的Radon变换对零均值噪声是稳健的。 由于人脸图像是由有限个离散的像素点组成的,式(5)并不适用。文献[11]通过推导得出Radon变换后图像的信噪比可表示为: SNRRadon=10lg(1.7NR)+SNRimage (6) 其中,SNRimage表示图像的信噪比,SNRRadon表示Radon变换后的信噪比,NR表示Radon变换时的图像半径。 式(6)表明,经过Radon变换后,图像的信噪比增加了10lg(1.7NR),与SNRimage相比,这是一个很大的数值(比如NR为64时,其值为20 db)。因此,可以认为人脸经过Radon变换后,提取的特征不易受噪声的影响,在文献[12]中对此也进行了比较详细的实验验证。 图像的Radon变换具有位移不变性、旋转不变性和比例不变性等特点[13~15],而人脸图像的采集过程中,由于各种因素,不可避免地会出现图像中人脸的旋转、大小不一和噪声,采用Radon变换对人脸图像进行处理后,可减轻这些因素造成的人脸特征鉴别性变差的问题。图4和图5分别给出了原始的人脸图像和经过预处理后的人脸图像的Radon变换结果。经过同态滤波器处理后,图像的光照分布明显变得比较均衡,被阴影部分覆盖的细节也变得更清晰。 Figure 4 Original face image and its Radon transform图4 原始人脸图像及其Radon变换 Figure 5 Light-corrected face image and its Radon transform图5 光照矫正后人脸图像及其Radon变换 4数据降维及分类 为了提高计算效率,去除冗余信息,通常在分类前需要进行数据降维。常见的数据降维方法有主成分分析、线性判别式分析、局部保留投影及对它们的改进算法。在这些算法中,主成分分析和局部保留投影是非监督算法,线性判别式分析方法是监督学习算法。本文选择二维线性判别式分析方法2DLDA(Two Dimension Linear Discriminant Analysis)[16]和二维主成分分析方法2DPCA(Two Dimensional Principal Component Analysis)[17]对经过Radon变换后的人脸图像进行降维,并和LBP结合2DPCA/2DLDA的算法进行识别性能比较。为了计算的有效性,本文选择最近邻分类器对经过降维后的数据进行分类。 5实验结果及分析 Yale(http://cvc.yale.edu/projects/yalefaces/yalefaces.html)和PIE[18]数据库被用来进行算法性能测试。Yale人脸数据库含有15个不同个人的165张人脸图像,其中每人有11张包括光照变化、表情变化以及是否戴眼睛等。PIE人脸数据库包含有68个人的41 368张多姿态、光照和表情变化的面部图像,本文选择正面光照图像子集作为实验样本,其中每人有24张不同光照条件下的人脸图像。为了提高运算效率,实验中将所有图像用手工裁剪并缩放至32×32像素。 同态滤波器在γH>1,γL<1时,可增强人脸图像的高频成分,同时降低低频成分。而人脸的高频成分主要来自于其细节部分,也就是眼睛、鼻子和嘴巴等部分,这些信息在人脸识别中具有重要的作用。但是,γH太大将引入过多的噪声。而γH和γL的选择在理论上并无具体的指导方法。为了能够选择合适的γH和γL,本实验首先通过改变γH和γL的值,看其变化对识别精度的影响,然后选择γH和γL的值。 每人选取前四个样本作为训练样本,其余样本作为测试样本,降维方法采用2DPCA。表1给出了在γH和γL取值不同时算法的识别率,其中2DPCA提取的特征维数固定为13。从表1能够发现,在2>γH>1,γL<1时,识别率没发生变化,但在γH≥2时,识别率有所下降。其主要原因可能是γH太大时引入了过多的噪声。因此,本文算法在后面的实验中γH和γL的取值范围为2>γH>1,γL<1。 Table 1 Recognition rates of 2DPCA under various γH and γL 为了进一步测试提出的方法在不同特征维数下的识别性能,图6给出了六种方法的识别率随特征维数变化的曲线,其中样本的选择同上,每人选前四个图片作为训练样本,其余图片作为测试样本。从图6能够看到,经过光照预处理和Radon变换后,2DPCA和2DLDA的识别性能较未经处理、变换时有了较大幅度的提高。尤其是Radon+2DLDA,其识别性能远高于2DLDA,最好识别性能达到了95.29%。 Figure 6 Recognition rate curves under various feature dimensions图6 识别率随特征维数变化曲线 另外,本文也测试了算法在训练样本不同时的识别性能。每人随机选择P(P=2,3,4,5,6)张图像作为训练样本,其余作为测试样本。这种选择重复10次,计算每个P下六种算法的平均识别精度。表2给出了六种算法在不同训练样本数下的最佳平均识别精度。从表2能够看到,经过预处理和Radon变换后,得到的特征具有更好的光照不变性和几何不变性,其鉴别性远高于未经光照处理而直接在原始图像上提取的特征,尤其用2DPCA提取特征时表现得更为突出。 每人随机选择12张图像作为训练样本,其余图像作为测试样本,实验重复10次,计算10次实验得到识别率的平均值,将其作为最终识别率。图7给出了六种算法识别率随特征维数变化的曲线图。 Figure 7 Recognition rate curves of six algorithms under various feature dimensions on PIE database图7 在PIE数据库上算法识别率随特征维数变化曲线 从图7能够发现,经过预处理和Radon变换后,用2DPCA/2DLDA降维后算法的识别性能大幅度提高,且识别精度在达到最高时不随特征维数的增加而下降,较2DPCA和2DLDA具有更好的鲁棒性。 Table 2 Comparison of the best recognition rates under various number of training samples 通过在Yale和PIE人脸数据库上的实验结果也能发现,结合LBP和2DPCA/2DLDA的识别方法在PIE数据库上具有较好的识别性,但在Yale数据库上识别性能较差,其主要原因是Yale数据库的图片中包含有背景,而在PIE数据库中只有人脸的五官部分。与LBP+2DPCA/2DLDA方法相比较,本文提出的方法在不管是否包含有背景成分的图像中,识别性能都比较好,具有更好的鲁棒性。 从上述实验结果表明,经过预处理和Radon变换后,得到的人脸特征具有更好的鉴别性。其主要原因是经过预处理后,使得人脸图像的光照更均匀,消除了部分光照不均造成的特征的变化,同时Radon变换降低了因为旋转、平移以及成像角度变换导致的人脸特征的改变。 6结束语 通过结合光照预处理、同态滤波器、Radon变换和2DPCA/2DLDA,提出了一种光照不变的人脸识别方法。在Yale和PIE人脸数据库上的实验结果表明,提出的方法较在原始人脸图像上直接进行降维得到的特征更具鉴别性。本文提出的方法是一种高精度的光照不变人脸识别算法,可用于具有光照变换与几何变化条件下人脸特征提取。 参考文献:附中文 [1]Yan Y,Wang Hi,Suter D,et al.Multi-subregion based correlation filter bank for robust face recognition[J].Pattern Recognition,2014,47(11):3487-3451. [2]Dong Chang-jian,Chen Xiu-hong,Chen Da-yao,et al.Supervised orthogonal locality preserving projection and its application in face recognition[J].Computer Engineering & Science,2014,36(8):1576-1580.(in Chinese) [3]Deng W, Hu J, Zhou X, et al. Equidistant prototypes embedding for single sample based face recognition with generic learning and incremental learning[J].Pattern Recognition,2014,47(12):3738-3749. [4]Ou W,You X,Tao D,et al.Robust face recognition via occlusion dictionary learning[J].Pattern Recognition,2014,47(4):1559-1572. [5]Hang S .An advanced motion detection algorithm with videoquality analysis for video surveillance systems[J].IEEE Transactions on Circuits and Systems for Video Technology,2011,21(1):1-14. [6]Luan X,Fang B,Liu L,et al.Extracting sparse error of robust PCA for face recognition in the presence of varying illumination and occlusion[J].Pattern Recognition,2014,47(2):495-508. [7]Han H,Shan S G,Chen X L,et al.A comparative study on illumination preprocessing in face recognition[J].Pattern Recognition,2013,46(6):1691-1699. [8]Cheng Xue-feng,Li Shun,Long Fei,et al.Illumination invariant face recognition based on Log-gabor filtering and LBP descriptor[J].Journal of Xiamen University(Nature Science),2014,53(3):359-363.(in Chinese) [9]Yang W,Guo W,Peng K,et al.Research on removing shadow in workpiece image based on homomorphic filtering[J].Procedia Engineering,2012,29:2360-2364. [10]Magli E, Olmo G, Presti L, et al. Pattern recognition by means of the Radon transform and the continuous wavelet transform[J].Signal Process,1999,73(3):277-289. [11]Ashok R,Noushath S. Subspace methods for face recognition [J].Computer Science Review,2010,4(1):1-17. [12]Khouzani K,Zadeh H.Rotation-invariant multiresolution texture analysis using Radon and wavelet transform[J].IEEE Transactions on Image Process,2005,14(6):783-795. [13]Jadhava D,Rotation H R.illumination invariant polynomial kernel Fisher discriminant analysis[J].Pattern Recognition Letters,2010,31(9):1002-1009. [14]Nacereddine N,Tabbonec S,Zioud D,et al.Similarity transformation parameters recovery based on Radon transform.Application in image registration and object recognition[J].Pattern Recognition,2015,48(7):2227-2240. [15]Hasegawa M,Tabbone S.Amplitude-only log Radon transform for geometric invariant shape descriptor[J].Pattern Recognition,2014,47(2):643-658. [16]Jadhav D,Holambe R.Feature extraction using Radon and discrete cosine transforms based features for face recognition[J].Neurocomputing,2009,72(7-9):1951-1959. [17]Li M,Yuan B. 2DLDA:A statistical linear discriminant analysis for image matrix[J].Pattern Recognition Letters,2005,26(5):527-532. [18]Yang J,Zhang D,Frangi A,et al.Two-dimensional PCA:A new approach to appearance-based face representation and recognition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2004,26(1):131-137. [19]Sim T,Baker S,Bsat M,et al.The CMU Pose,Illumination,and Expression(PIE) database of human faces[R].Tech Report CMU-RI-TR-01-02.Pittsburgh,PA:Robotics Institute,Carnegie Mellon University,2001. [2]董昌剑,陈秀宏,陈达遥.有监督正交局部保留投影及其在人脸识别中的应用[J].计算机工程与科学,2014,36(8):1576-1580. [8]程雪峰,李顺,龙飞,等.基于Log-Gabor滤波和LBP算子的光照不变人脸识别方法[J].厦门大学学报(自然科学版),2014,53(3):359-363. 齐永锋(1972-),男,甘肃武威人,博士,副教授,CCF会员(33467M),研究方向为模式识别。E-mail:qiyf@nwnu.edu.cn QI Yong-feng,born in 1972,PhD,associate professor,CCF member(33467M),his research interest includes pattern recognition. 火元莲(1973-),女,甘肃兰州人,博士,副教授,研究方向为数字信号处理。E-mail:hylqqq@nwnu.edu.cn HUO Yuan-lian,born in 1973,PhD,associate professor,her research interest includes digital signal processing. An illumination invariant face recognition method based on homomorphic filters and Radon transform QI Yong-feng1,HUO Yuan-lian2 (1.College of Computer Science and Engineering,Northwest Normal University,Lanzhou 730070; 2.College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,China) Abstract:In order to reduce the effect of illumination changes on face recognition accuracy, we propose a face recognition method combining homomorphic filters with Radon transform. Firstly, we filter face images by homomorphic filters, then Radon transform is implemented and the feature dimension is reduced with 2DPCA/2DLDA.Experiment results on Yale and PIE face databases show that the recognition accuracy of the proposed method is better than the 2DPCA and 2DLDA methods under large illumination changes. Key words:homomorphic filter;Radon transform;face recognition 作者简介: doi:10.3969/j.issn.1007-130X.2015.12.030 中图分类号:TP391.4 文献标志码:A 基金项目:国家自然科学基金资助项目(61262056) 收稿日期:修回日期:2015-05-06 文章编号:1007-130X(2015)12-2393-06
flow chart using the homomorphic filter
图1同态滤波器进行人脸图像预处理流程图



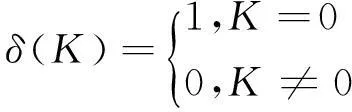




5.1 在Yale人脸数据库上的实验结果
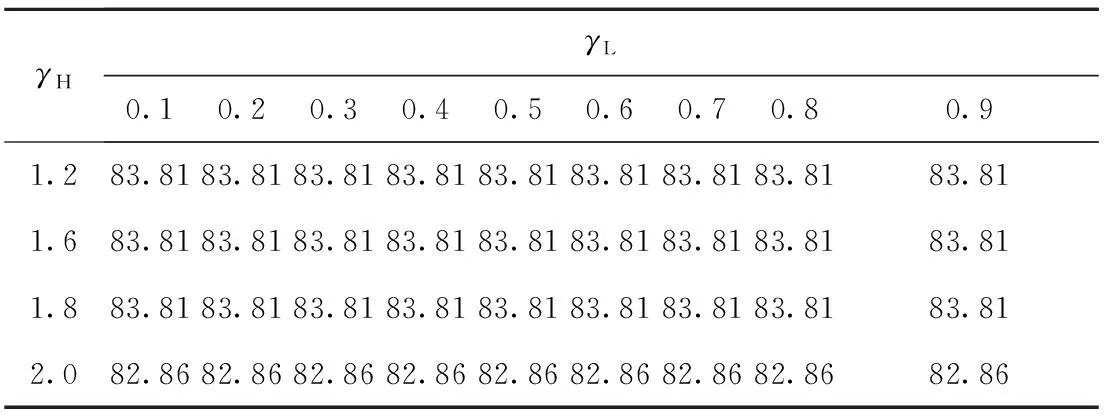

5.2 在PIE数据库上的实验结果





