考虑优先级的广义犹豫模糊信息集成方法*



考虑优先级的广义犹豫模糊信息集成方法*

通信地址：510641 广东省广州市天河区华南理工大学工商管理学院Address:School of Business Administration,South China University of Technology,Tianhe District,Guangzhou 510641,Guangdong,P.R.China

杨建辉,阮传扬

(华南理工大学工商管理学院，广东 广州510641)

摘要：研究了在属性之间存在优先级的情况下的广义犹豫模糊信息集成问题。考虑到属性优先级以及属性元素的统一程度的双重影响，首先给出了犹豫模糊信息下的熵值求法，并在其基础上提出了优先级混合赋权方法。之后，在该优先级混合赋权方法的基础上提出了广义犹豫模糊优先级混合几何(GHFPHG)算子，并给出了该类算子的优良特性。最后，利用案例验证了本文所提方法的实用性和有效性。

关键词：犹豫模糊集；多属性决策；广义犹豫模糊集成算子；优先级；熵值

1引言

犹豫模糊集HFS(Hesitant Fuzzy Set)是Torra V[1]在模糊集FS(Fuzzy Set)基础上提出的一类广义模糊集，HFS最大的特点是允许一个元素属于一个集合的隶属度可以同时出现几个不同的评价值，当决策小组针对某一个元素属于一个集合的隶属度不能达成一致意见时(也即呈现犹豫状态)，犹豫模糊集能够有效地刻画这一现象，是一种非常有用的工具。在目前的大数据浪潮下，如何对大数据信息(尤其是犹豫模糊信息)进行识别和精简显得尤为重要。因此，信息集成方法引起了越来越多学者的关注。信息集成就是利用大量信息融合成少量信息的一个关键技术，特别是加入偏好信息的信息集成方法。Bedregal B[2]详细研究了具有典型犹豫模糊现象的所有可能隶属水平的信息集成因子。Xia M M和Xu Z S[3]在直觉模糊信息集成算子的基础上详细给出了犹豫模糊加权平均HFWA(Hesitant Fuzzy Weighted Average)算子和犹豫模糊加权几何HFWG(Hesitant Fuzzy Weighted Geometric)算子等犹豫模糊信息集成算子。针对属性值存在关联关系的情况，Xu Z S和Cai X Q[4]定义了区间幂均融合算子，并用区间值之间的支持程度来确定权重信息。Yager R R[5]对Bonferroni算子进行了讨论，并将有序加权平均OWA(Ordered Weighted Average)和Choquet积分结合进来共同反映数据之间的内在联系。Wei G[6]和Yu D J等[7]在优先级集成PA(Prioritized Aggregation)因子[8]的基础上提出了新的犹豫模糊优先级信息集成因子。

通过现有的文献资料不难发现，犹豫模糊信息集成算子中一个关键因素就是偏好信息的集成方法，信息的偏好侧重点各不相同，现有的反映偏好信息的方法主要是采用Choquet积分和优先级集成(PA)因子，而在信息集成中具体从属性自身信息量的多少以及离散程度出发，结合属性的优先级进行定权的方法截止目前还未见有所研究。基于此，本文从犹豫模糊信息出发，研究一种新的属性信息权重确定方法，即基于熵值的优先级混合加权方法。之后，在该优先级混合加权方法基础上提出一种广义犹豫模糊优先级混合几何GHFPHG(Generalized Hesitant Fuzzy Prioritized Hybrid Geometric)算子，并讨论该类算子存在的特性。最后，利用应急预案评估的数值算例验证本文所提方法的可行性和优越性。

2预备知识

著名数学以及控制理论专家Zadeh L A[9]首次提出用隶属函数来表达不确定的信息，这一数学方法即为模糊集。犹豫模糊集是广义的模糊集，其特点是允许一个属性中同时出现多个可能的评价值。

定义1[1,3]若存在一个非空集合X={x1,x2,…,xn}，则犹豫模糊集即为从X={x1,x2,…,xn}到[0,1]的一个子集的函数，可以用如下数学公式表示：

(1)

其中,hE(x)表示隶属于[0,1]的几个可能的数的集合，x∈X表示在集合E中的隶属度。

定义2[3]若存在一个非空犹豫模糊集合h，则h的得分函数为：

(2)

其中，#h为犹豫模糊集h中的元素个数。

假设存在两个非空犹豫模糊集h1和h2，若s(h1)≻s(h2)，则h1≻h2，若s(h1)=s(h2)，则h1=h2。

根据犹豫模糊集的特性及其运算规则，Xia Mei-mei[10]给出了基于阿基米德T模和S模的犹豫模糊运算,规则如下：

定义3[10]假设h、h1和h2为三个犹豫模糊集，则:

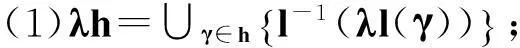
(3)h1⊗h2=∪γ1∈h1,γ2∈h2{k-1(k(γ1)+k(γ2))};

(4)h1⊕h2=∪γ1∈h1,γ2∈h2{l-1(l(γ1)+l(γ2))}。

其中，l(t)=k(1-t)。

一个严格的阿基米德T模是由一个加性的发生器k产生的，Klement定义为：T(x,y)=k-1(k(x)+k(y))，k:[0,1]→[0,+∞]为严格递减的函数且k(1)=0。由l(t)=k(1-t)，则阿基米德S模可表示为S(x,y)=l-1(l(x)+l(y))。

3广义犹豫模糊优先级混合集成算子

信息集成是犹豫模糊集理论的重点研究内容之一，但是大多数学者都是假定属性之间是独立的，并没有考虑属性之间的优先级关系。但是，在现实生活中，属性之间往往存在某种程度的优先级关系，并且犹豫模糊集元素的数量也会影响评价数据的可信程度。因此，本文提出一种既能考虑属性优先级又能同时考虑到犹豫模糊集中元素的离散程度的信息集成因子：广义犹豫模糊优先级混合几何(GHFPWG)算子。

3.1　基于熵值的优先级混合赋权方法

本文给出一种混合赋权方法，不仅可以考虑属性优先级，而且又能考虑到属性数据的统一程度。详细步骤如下[11,12]：

(1)评审专家组给出属性偏好信息，即属性优先级排序。

(2)通过计算第j项属性的熵值ej来确定相邻优先级属性xj与xj+1重要性程度之比rj：

(3)

(4)

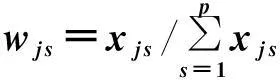
对于第j项属性，属性内的犹豫模糊信息差异性越小，则ej越大；当所有专家对第j项属性的评价数据全部相等时，此时专家意见高度统一，在犹豫模糊集中仅保留一个数据，则令ej=emax=1；当第j项属性的专家评价数据相差较大时，ej较小，该项属性的评价数据的可信程度较低，因此所起的作用也应当较小。

(3)根据给出的rj值，按照属性优先级从高到低的顺序计算优先级排序在第k个属性的权重tk为：

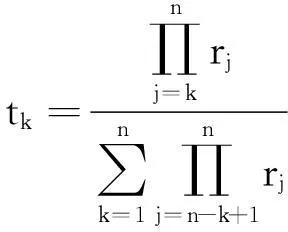
(5)

3.2　广义犹豫模糊优先级混合几何(GHFPHG)算子

基于现有的犹豫模糊信息集成算子以及考虑属性优先级的熵值组合赋权方法，我们可以定义广义犹豫模糊优先级混合几何(GHFPHG)算子。

定义4设一组犹豫模糊数hj(j=1,2,…,n)，且设GHFPHG:Ωn→Ω,若

GHFPHG(h1,h2,…,hn)=

(6)

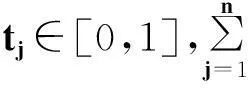
根据犹豫模糊集的运算规则，可以得到如下的定理以及推论：

定理1设一组犹豫模糊数hj(j=1,2,…,n)，则通过GHFPHG算子集结后仍然为犹豫模糊数，且:

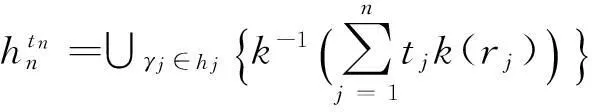
(7)

其中,tj(j=1,2,…,n)表示第j个属性的基于熵值的优先级混合权重。

定理2若所有犹豫模糊数满足h1=h2=…=hn=h*，tj(j=1,2,…,n)表示第j个属性基于熵值的优先级混合权重，则有:

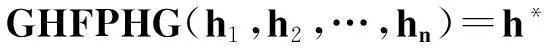
(8)

GHFPHG(h1,h2,…,hn)=

(9)

GHFPHG(h1,h2,…,hn)=

(10)

定理3设一组犹豫模糊数hj(j=1,2,…,n)，tj(j=1,2,…,n)表示第j个属性基于熵值的优先级混合权重，若λ>0，则：

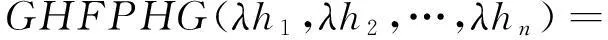
(11)

定理4设两组犹豫模糊数hj(j=1,2,…,n)、fj(j=1,2,…,n)，tj(j=1,2,…,n)表示第j个属性基于熵值的优先级混合权重，则：

GHFPHG(h1⊗f1,h2⊗f2,…,hn⊗fn)=GHFPHG(h1,h2,…,hn)⊗GHFPHG(f1,f2,…,fn)

(12)

推论3设一组犹豫模糊数hj(j=1,2,…,n)，tj(j=1,2,…,n)表示第j个属性基于熵值的优先级混合权重，若f为一犹豫模糊数，则：

GHFPHG(h1⊗f,h2⊗f,…,hn⊗f)=GHFPHG(h1,h2,…,hn)⊗f

(13)

推论4设一组犹豫模糊数hj(j=1,2,…,n)，tj(j=1,2,…,n)表示第j个属性基于熵值的优先级混合权重，若f为一犹豫模糊数且λ>0，则：

(14)

定理5设一组犹豫模糊数hj(j=1,2,…,n)，tj(j=1,2,…,n)表示第j个属性基于熵值的优先级混合权重，则:

GHFPHG(h1,h2,…,hn)≤GHFPHA(h1,h2,…,hn)

(15)

假设赋予函数k具体的函数式，则会产生不同的情况：

情况1若k(t)=-log(t)，则GHFPHG算子转化为：

GHFPHG(h1,h2,…,hn)=

(16)

其中，tj(j=1,2,…,n)表示第j个属性基于熵值的优先级混合权重。我们称这种形式的算子为犹豫模糊优先级混合几何HFPHG(Hesitant Fuzzy Priorited Hybrid Geometric)算子。

情况2若k(t)=log((2-t)/t)，则GHFPHG算子转化为：

GHFPHG(h1,h2,…,hn) =

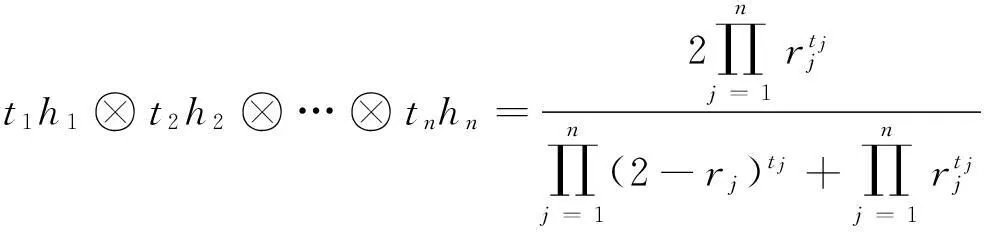
(17)

其中，tj(j=1,2,…,n)表示第j个属性基于熵值的优先级混合权重。我们称这种形式的算子为犹豫模糊爱因斯坦优先级混合几何HFEPHG(Hesitant Fuzzy Einstein Prioritized Hybrid Geometric)算子。

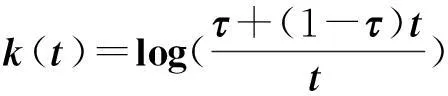
GHFPHG(h1,h2,…,hn) =

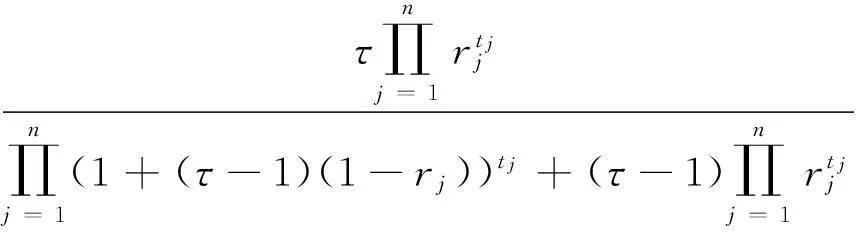
(18)

其中，tj(j=1,2,…,n)表示第j个属性基于熵值的优先级混合权重。我们称这种形式的算子为犹豫模糊哈马克优先级混合几何HFHPHG(Hesitant Fuzzy Hamacher Prioritized Hybrid Gometric)算子。特别地，当τ=1时，则HFHPHG算子退化为情况1中的HFPHG算子；当τ=2时，则HFHPHG算子退化为情况2中的HFEPHG算子。

4基于GHFPHG算子的突发事件应急预案

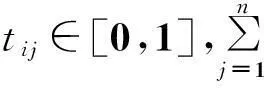
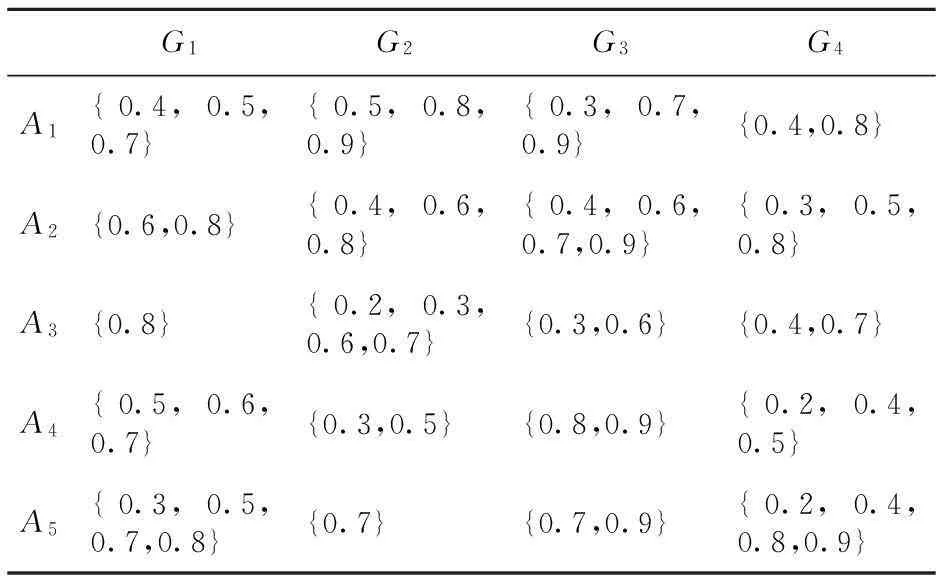
Table 1　Hesitant fuzzy decision making matrix

Table 2　Attribute entropy matrix

方法1为了得到最优应急预案，利用GHFPHG算子且令k(t)=-log(t)构建了一种犹豫模糊优先级多属性决策方法，具体步骤如下：

步骤1首先利用公式(3)计算每个方案Ai∈A关于每个属性Gj∈G的评估值的熵值，构成熵值矩阵如表2所示，然后在熵值的基础上利用公式(5)计算基于熵值的优先级混合权重tij(i=1,2,…,m;j=1,2,…,n)。

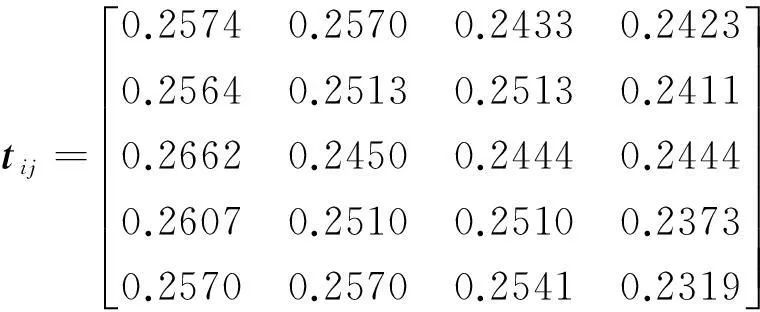
步骤2若k(t)=-log(t)，则GHFPHG算子转化为：

GHFPHG(h1,h2,…,hn) =

(19)

利用GHFPHG算子集成犹豫模糊矩阵H=(hij)m×n，得出应急预案Ai(i=1,2,…,5)的综合表现值hi(i=1,2,…,5)。由于数据过多，本文仅以综合表现值h1为例，其他类似。

h1={0.395 0,0.467 2,0.418 3,0.494 8,0.456 2,0.539 6,0.445 7,0.527 2,0.472 0,0.558 4,0.514 7,0.608 9,0.459 4,0.543 4,0.486 5,0.575 5,0.530 6,0.627 6,0.485 4,0.574 2,0.514 1,0.608 1,0.560 6,0.663 1,0.547 7,0.647 9,0.580 1,0.686 2,0.632 6,0.748 3,0.564 5,0.667 8,0.597 9,0.707 3,0.652 0,0.771 3,0.516 0,0.610 4,0.546 5,0.646 5,0.596 0,0.704 9,0.582 3,0.688 7,0.616 7,0.729 4,0.672 5,0.795 4,0.600 1,0.709 9,0.635 6,0.751 9,0.693 1,0.819 9}

步骤3根据犹豫模糊得分函数公式(见定义2)计算hi(i=1,2,…,m)的得分如下:

s(h1)=0.597 1,s(h2)=0.600 0,s(h3)=0.529 2,s(h4)=0.515 5,s(h5)=0.631 1

由于s(h5)≻s(h2)≻s(h1)≻s(h3)≻s(h4),则可选方案排序结果为：A5≻A2≻A1≻A3≻A4，因此最优应急预案为A5。

方法2为了得到最优应急预案，若利用GHFPHG算子且令k(t)=log((2-t)/t)构建了一种犹豫模糊优先级多属性决策方法，详细步骤如下：

步骤1′见步骤1；

步骤2′由于k(t)=log((2-t)/t)，则GHFPHG算子转化为：

GHFPHG(h1,h2,…,hn)=

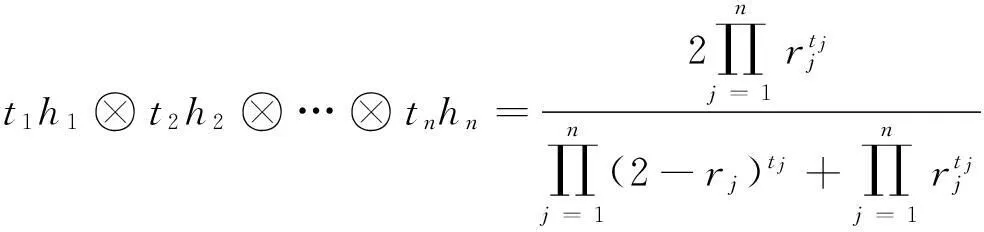
(20)

利用GHFPHG算子集成犹豫模糊矩阵H=(hij)m×n，得出应急预案Ai(i=1,2,…,5)的综合表现值hi(i=1,2,…,5)。由于数据过多，本文仅以综合表现值h1为例，其他类似。

h1={0.396 6,0.489 9,0.528 5,0.477 5,0.583 0,0.626 0,0.420 6,0.517 8,0.557 8,0.505 0,0.614 1,0.658 2,0.463 1,0.566 6,0.608 8,0.553 0,0.667 8,0.713 8,0.456 2,0.558 8,0.600 6,0.545 3,0.659 2,0.705 0,0.482 8,0.589 1,0.632 2,0.575 1,0.692 4,0.739 1,0.529 5,0.641 6,0.686 8,0.627 0,0.749 3,0.797 5,0.475 0,0.580 2,0.623 0,0.566 4,0.682 7,0.729 2,0.502 4,0.611 2,0.655 2,0.596 9,0.716 4,0.763 8,0.550 2,0.664 8,0.710 7,0.649 9,0.774 1,0.822 9}

步骤3′根据犹豫模糊得分函数公式(见定义2)计算hi(i=1,2,…,m)的得分如下:

s(h1)=0.609 1,s(h2)=0.609 2,s(h3)=0.542 3,s(h4)=0.530 1,s(h5)=0.644 2

由于s(h5)≻s(h2)≻s(h1)≻s(h3)≻s(h4),则可选方案排序结果为：A5≻A2≻A1≻A3≻A4，因此最优应急预案为A5。

方法3为了与现有方法进行对比，若本文采用文献[3]中的HFHA算子构建犹豫模糊多属性决策方法，假设权重数据已知且为方法1中所得权重，具体步骤如下：

步骤1″采用方法1中的基于熵值的优先级混合权重tij(i=1,2,…,m;j=1,2,…,n)。

步骤2″由文献[3]可知HFHA算子为：

HFHA(h1,h2,…,hn)=t1h1⊕t2h2⊕…⊕tnhn=

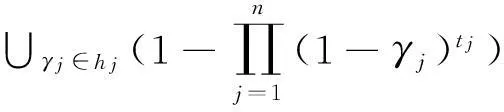
(21)

利用HFHA算子集成犹豫模糊矩阵H=(hij)m×n，得出应急预案Ai(i=1,2,…,5)的综合表现值hi(i=1,2,…,5)。由于数据过多，本文仅以综合表现值h1为例，其他类似。

h1={0.405 6,0.516 3,0.629 8,0.544 5,0.629 4,0.716 3,0.432 8,0.538 5,0.646 7,0.565 4,0.646 4,0.729 3,0.502 7,0.595 4,0.690 3,0.618 9,0.689 9,0.762 7,0.530 3,0.617 8,0.707 4,0.640 1,0.707 1,0.775 8,0.551 8,0.635 3,0.720 9,0.656 6,0.720 6,0.786 1,0.607 1,0.680 3,0.755 3,0.698 9,0.755 0,0.812 5,0.606 9,0.680 2,0.755 2,0.698 8,0.754 9,0.812 4,0.625 0,0.694 8,0.766 4,0.712 6,0.766 1,0.821 0,0.671 2,0.732 4,0.795 2,0.748 0,0.795 0,0.843 1}

步骤3″根据犹豫模糊得分函数公式(见定义2)计算hi(i=1,2,…,m)的得分如下:

s(h1)=0.675 9,s(h2)=0.657 0,s(h3)=0.612 6,s(h4)=0.622 0,s(h5)=0.709 7

由于s(h5)≻s(h1)≻s(h2)≻s(h4)≻s(h3),则可选方案排序结果为：A5≻A1≻A2≻A4≻A3，因此最优应急预案为A5。

由以上结果可知，利用三种方法计算的最优应急预案全为A5，从具体排序结果可以发现本文所提方法主要优点如下：

(1)在GHFPHG算子中，当k(t)取不同的形式时，对决策结果并没有显著影响，排序结果完全相同，证明GHFPHG算子具有稳定性的特征。

(2)文献[3]仅仅考虑了属性信息大小的影响，与之相比，本文不仅考虑了属性之间的优先级关系，而且也考虑了属性数据的统一程度，因此具有良好的区分度。

(3)当选择不同的集成算子时，即HFHA和GHFPHG算子，若两个方案的得分非常接近时，由两个集成算子所得到的结果会有微小差别，也即侧重点不同。现有的HFHA算子要求必须事先有权重数据且侧重于群体决策，而GHFPHG算子可以直接利用基于熵值的优先级混合赋权方法得出客观权重数据，主要侧重于个体决策，决策者可以根据个人偏好进行选择。在属性权重信息不明确的情况下，利用本文提出的GHFPHG算子对犹豫模糊信息进行信息集成，计算操作相对简单、科学，可以有效地对候选方案进行抉择。

5结束语

本文研究了在属性之间存在优先级的前提下的广义犹豫模糊信息集成问题。为了对多属性决策中的犹豫模糊信息进行区别和集成，本文首先提出了基于熵值的优先级混合赋权方法，新赋权方法同时考虑到了属性优先级以及属性元素的离散程度的双重影响，较好体现了犹豫模糊信息间的内在联系。其次，在优先级混合赋权方法的基础上提出了GHFPHG算子，该类算子的特点是将属性优先级跟属性评价信息的统一程度有机地融合在一起。最后，本文利用该类算子构建了在属性具有优先级的条件下的广义犹豫模糊多属性决策方法，并用应急预案评估的数值案例验证了本文所提方法的实用性和有效性。

参考文献:附中文

[1]Torra V. Hesitant fuzzy sets[J]. International Journal of Intelligent Systems,2010,25(6):529-539.

[2]Bedregal B,Reiser R,Bustince H,et al.Aggregation functions for typical hesitant fuzzy elements and the action of automor-

phisms[J]. Information Sciences,2014,255:82-99.

[3]Xia M M,Xu Z S. Hesitant fuzzy information aggregation in decision making[J]. International Journal of Approximate Reasoning,2011,52(3):395-407.

[4]Xu Z S,Cai X Q. Uncertain power average operators for aggregating interval fuzzy preference relations[J]. Group Decision and Negotiation,2012,21(3):381-397.

[5]Yager R R. On generalized Bonferroni mean operators for multi-criteria aggregation[J]. International Journal of Approximate Reasoning,2009,50(8):1279-1286．

[6]Wei G. Hesitant fuzzy prioritized operators and their application to multiple attribute decision making[J]. Knowledge-Based Systems,2012,31:176-182.

[7]Yu D J,Zhang W Y,Xu Y J. Group decision making under hesitant fuzzy environment with application to personnel evaluation[J]. Knowledge-Based Systems,2013,32:1-10.

[8]Yager R R. Prioritized aggregation operators[J]. International Journal of Approximate Reasoning,2008,48(1)：263-274.

[9]Zadeh L A. Fuzzy sets[J]. Information and Control,1965,8(3):338-353.

[10]Xia Mei-mei. Research on fuzzy decision making information aggregation techniques and measures[D]. Nanjing:Southeast University,2012.(in Chinese)

[11]Li Gang. The science and technology evaluation model and its empirical research based on entropy-revised G1 combination weighting[J]. Soft Science,2010,24(5):31-36.(in Chinese)

[12]Ruan C Y,Yang J H. Software quality evaluation model based on weighted mutation rate correction incompletion G1 combination weights[J]. Mathematical Problems in Engineering,2014(2014),Article ID 541292.

[10]夏梅梅. 模糊决策信息集成方式及测度研究[D]. 南京：东南大学,2012.

[11]李刚. 基于熵值修正G1组合赋权的科技评价模型及实证[J]. 软科学,2010,24(5):31-36.

杨建辉(1960-),男,广东广州人，博士后,教授,研究方向为管理决策。E-mail:bmjhyang@scut.edu.cn

YANG Jian-hui,born in 1960,post doctor,professor,his research interest includes management decision-making.

Generalized hesitant fuzzy information aggregation method with prioritized levels

YANG Jian-hui,RUAN Chuan-yang

(School of Business Administration,South China University of Technology,Guangzhou 510641,China)

Abstract:In this paper, we investigate the generalized hesitant fuzzy information aggregation issues in which the attributes are on different priority levels. Considering the impact of both attributes’ priority levels and the dispersion degree of hesitant fuzzy elements, we first give the entropy based on hesitant fuzzy information, and propose a prioritized hybrid weighted method accordingly. Then, we put forward generalized hesitant fuzzy prioritized hybrid geometric (GHFPHG) operator based on the hybrid weighted method. Furthermore, we discuss some desirable properties of the proposed prioritized operator. Finally, the practicality and effectiveness of the proposed approach are verified by a practical example.

Key words:hesitant fuzzy sets;multiple attribute decision making;generalized hesitant fuzzy integration operator;priority level;entropy

作者简介:

doi:10.3969/j.issn.1007-130X.2015.12.032

中图分类号：C934

文献标志码：A

基金项目：广东省委省政府重点项目(N6131810)；中央高校基本科研业务资助项目(Y6090020)

收稿日期：修回日期：2015-09-07

文章编号：1007-130X(2015)12-2405-06