三相LCL光伏并网逆变器的准比例谐振重复控制研究
邓宇恩,粟时平,刘桂英,杨 安,桂永光,颜一帆
(1. 长沙理工大学 电力系统安全运行与控制湖南省高校重点实验室,湖南长沙410114;2. 江苏省电力公司 宿迁供电公司,江苏 宿迁 223800;3.湖南省电力公司 检修公司,湖南长沙410114)
三相LCL光伏并网逆变器的准比例谐振重复控制研究
邓宇恩1,粟时平1,刘桂英1,杨安1,桂永光2,颜一帆3
(1. 长沙理工大学 电力系统安全运行与控制湖南省高校重点实验室,湖南长沙410114;2. 江苏省电力公司 宿迁供电公司,江苏 宿迁 223800;3.湖南省电力公司 检修公司,湖南长沙410114)
摘要:针对LCL型光伏并网逆变器控制系统,提出了一种重复控制并联准比例谐振控制的复合控制策略,以改善并网逆变器的输出电流质量。该控制策略结合了两者的优点,其中准比例谐振控制能够保证系统的动态性能,并提高系统抗电网频率波动的能力,而重复控制在并网系统稳定以后可以抑制电网的周期性扰动,提高电流波形跟踪精度,从而获得更高质量的并网电流波形。通过Matlab/Simulink进行仿真实验,证明了这种复合控制策略的有效性和可行性,使系统具有良好的动、稳态性能和抗干扰能力,降低了并网电流的谐波含量。
关键词:光伏并网;LCL滤波器;重复控制;准比例谐振控制;复合控制
中图分类号:TM464
文献标识码:A
DOI:10.3969/j.issn.1672-0792.2015.10.007
收稿日期:2015-07-30。
作者简介:邓宇恩(1991-),男,硕士研究生,研究方向为新能源并网发电技术,E-mail:dengyuen489@126.com。
Abstract:Considering the photovoltaic grid-connected inverter system with LCL filter,a compound strategy based on repetitive control parallel with quasi proportional resonant(Quasi-PR) control is proposed, with the purpose to improve the quality of output current. The compound strategy combines the advantages of the two Quasi-PR control can ensure the dynamic performance of the system. And it can also improve the ability against power grid frequency fluctuation. While repetitive control can suppress the periodic disturbance of the power grid after the grid-connected system has been stabilized. It can also improve the tracking accuracy of the current waveform. As a result a higher quality of the grid-connected current waveform can be obtained. Simulation by Matlab/Simulink can verify the effectiveness and feasibility of the proposed compound strategy, which ensures the high quality performance of the system in both dynamic and steady-state accuracy,improvies the disturbance rejection and reduces the harmonic content of the grid-connected current.
Keywords:photovoltaic grid-connected;LCL filter;repetitive control;Quasi-PR control;compound control

0引言
太阳能作为一种取之不竭的可再生能源,具有绿色环保无污染的特点,成为了最具应用前景的新型能源[1]。太阳能的有效利用主要通过光伏并网发电的方式实现,而并网逆变器作为连接光伏发电系统与电网的桥梁,直接影响着并网电流的质量,因此,研究光伏并网逆变系统的拓扑结构和电流控制方法具有重要的意义[2]。
光伏并网逆变系统中,通常在逆变器输出端采用适当的输出滤波器来改善并网电流质量。近年来,LCL滤波器成为人们的研究热点,相对于传统的L,LC滤波器,LCL型滤波器具有在高频段快速衰减的特性,以较小的硬件体积便可实现对开关频率处谐波的抑制[3]。但是由于LCL滤波器是一个三阶多变量系统,特性比较复杂,给并网逆变器的控制系统设计提出了更高要求[4,5]。
在LCL型并网逆变器的电流控制中,传统比例积分(Proportional Integral,PI)控制结构简单,但在跟踪正弦的参考电流信号时存在较大的稳态误差。比例谐振(Proportional Resonant,PR)控制在谐振频率处获得高增益,可以实现对基波信号的“无静差”跟踪,但在有效抑制多个频率谐波时,需加入相应数量的PR控制器,这无疑增加了控制的复杂程度[6]。重复控制是一种基于内模原理的控制方法,仅需一个内模控制器就能够抑制各次谐波,在稳态时能够实现对复杂交流信号的零误差跟踪,因此受到了广泛关注。然而,单一的重复控制动态性能差,无法实现短于一个周波的动态响应。因此,重复控制一般是同其他控制方法配合起来使用[7~9]。文献[7]提出了一种在dq旋转坐标系下由重复控制与PI控制相并联的组合控制策略,保证系统稳态控制精度的同时可以改善系统的动态性能。然而实际电网频率往往存在一定的波动,重复控制和PI控制都会受到较大的影响,使并网电流质量变差。为此,本文提出了一种基于αβ静止坐标系的重复控制与准比例谐振(Quasi Proportional Resonant,QPR)控制相并联的复合控制策略,利用准PR控制来提高系统抗电网频率偏移的能力,同时保证系统具有良好的动态性能,利用重复控制的无静差跟踪来提高系统的稳态性能,理论分析和仿真结果证明了该复合控制策略的优越性和可行性。
1三相光伏并网逆变器系统模型
1.1 系统主电路拓扑结构
图1所示为基于LCL型滤波器的三相光伏并网逆变系统主电路拓扑结构图。逆变器输出端采用LCL型滤波电路与电网连接,可以有效地抑制并网电流中由开关动作引起的高次谐波,从而获得高质量的并网电流波形。

图1 光伏并网逆变系统结构图
1.2 系统数学模型及控制结构
为了方便对LCL型并网逆变器的控制策略进行研究,需要对选定的逆变器拓扑结构进行数学建模。以图1中LCL滤波器的电感电流i1K,i2K以及电压uCK作为系统数学模型的状态变量,根据图1及基尔霍夫定律得到系统在abc三相静止坐标系下的状态空间方程:(其中,k=a,b,c) 。
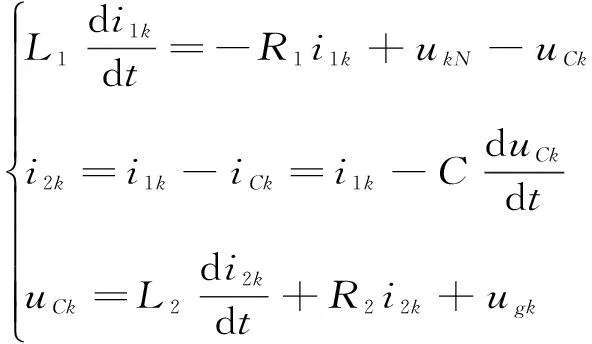
(1)
将该状态方程通过Clark变换,可得到αβ两相静止坐标系下的状态方程:



(2)

在同一αβ两相静止坐标系下,重复控制和准PR控制可以同时对正弦的基准交流信号进行跟踪,而且无需对电流分量进行解耦,控制简单。
因此,为使并网逆变系统取得良好的动、稳态性能,本文提出了一种在同一坐标系下由重复控制与准PR控制相并联的复合控制策略,其控制结构示意图如图2所示。

图2 重复控制并联准PR控制结构图
2三相LCL型光伏并网系统控制策略
2.1 电容电流反馈控制
针对LCL型并网逆变器的谐振问题,采取电容电流反馈增大系统阻尼的有源阻尼控制方法,可以消除谐振尖峰[10]。因此,本文采用的电流双闭环控制结构如图3所示。

图3 双闭环控制系统结构框图
其中,kc为电容电流反馈系数,逆变器单元通常近似看成一个增益环节KPWM,一般取KPWM=0.5Udc,G(s)为由重复控制与准PR控制并联而成的并网电流控制环节。由双闭环控制结构图3可得电容电流内环传递函数为:
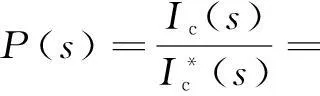
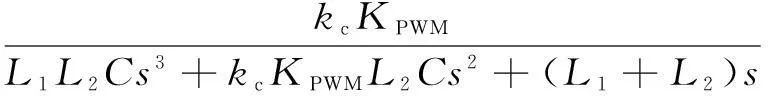
(3)
且P(s)即为图2中复合控制器的控制对象。
2.2 重复控制并联准PR控制的复合控制策略
重复控制源于控制理论中的内模原理[11]。重复控制的内模数学模型描述的是周期性信号,因而使得闭环控制系统能够无静差地跟踪周期信号。对于并网逆变器系统,其谐波信号的频率是基波信号频率的倍数,且具有周期性,即谐波信号在每个基波周期内均相同,因此使用一个内模控制器便能抑制各次谐波,使系统获得良好的稳态性能。传统重复控制的离散内模形式:

(4)
式中:N为一个周期的采样次数,即系统采样频率与系统基波频率的比值。
由于z-N的存在,使重复控制内模输出的控制量延迟一个基波周期,导致重复控制的动态性能变差。
比例谐振(PR)控制器的传递函数为

(5)
在并网逆变器应用中,PR控制在特定频率处的增益趋于无穷大,因此可以实现对特定正弦指令信号的无静差跟踪。但在实际系统中,理想的PR控制器难以实现,且容易受到电网频率偏移的影响,很难实现无静差跟踪。通常采用一种容易实现的准比例谐振控制器[12],其传递函数为:
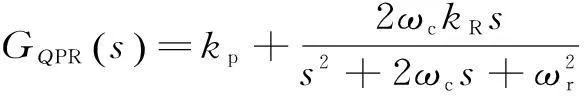
(6)
其中,令ωr=314 rad/s为谐振频率。准PR控制在谐振频率处的增益减小,但通过增加带宽提高了抗电网频率偏移能力,且具有较好的动态性能。
由上述分析可知,重复控制与准比例谐振控制具有一定的互补性,因此本文将两种控制器相并联,形成一种复合控制器。复合控制的离散形式结构如图4所示。

图4 复合控制结构图
图4中,iref为并网指令电流,i2为并网实际电流,P(z)为控制对象,GQPR(z)为准比例谐振控制器。重复控制器中,Q(z)为辅助补偿器[13];C(z)为针对等效控制对象P(z)设计的镇定补偿器,包括幅值补偿和相位补偿,通常取C(z)=krzkS(z)。图5为系统的控制结构模型。
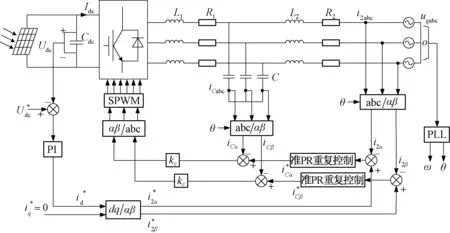
图5 LCL型三相光伏并网系统控制模型
3复合控制器的性能分析和参数设计
由复合控制结构图4可得,系统电流环传递函数为

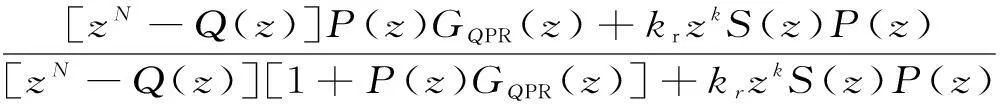
(7)由此可得其特征多项式为


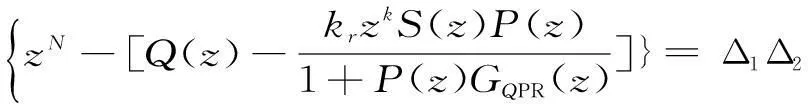
(8)由式(8)可得,若要使系统稳定,则需保证Δ1=0和Δ2=0的根均在单位圆内[14]。因此,复合控制系统稳定的必要条件为重复控制器和准PR控制器分别单独作用时系统均能保证稳定。并联准PR控制器后,将重复控制器的等效控制对象定义为P*(z),即

(9)当准PR控制器单独作用时,在图3的双闭环控制结构图中,令G(s)为GQPR(s)时,可得系统的闭环传递函数为

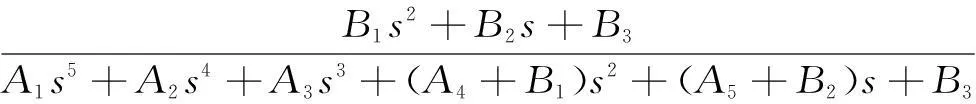
(10)其中


A2=2ωcL1L2C+L2CkcKPWM;



则对应的特征方程为:D(s)=A1s5+A2s4+A3s3+(A4+B1)s2+
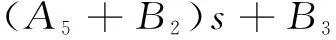
(11)根据劳斯稳定判据,可知系统稳定的充要条件与kp,kR,ωc和kc4个参数相关。本文采用零极点对消和极点配置的方法[15],求得系统稳定条件下各参数的取值范围。
在满足系统稳定的前提下,综合考虑复合控制器的特点,对准PR控制器参数进行设计:①为提高系统抗电网频率波动的影响,假设电网频率允许波动的范围为±0.8 Hz,则ωc/π=1.6,可得ωc=5;②根据基波频率附近的增益要求选取kR=100;③参数kp关系到系统的稳定性和抗干扰性,本文选取kp=4。确定准PR控制器的参数后,代入电路各参数值L1=10 mH,L2=5 mH,C=1.75 μF,kcKPWM=80,可以得到闭环系统的特性如图6所示。

图6 基于准PR控制的电流闭环伯德图
由图6可知,准PR控制器单独作用时:①基波频率处的增益接近为零,稳态误差较小;②基波频率处相位误差接近于零,系统较稳定。同时,采取的电容电流反馈法使系统的谐振峰得到了有效抑制。但系统的高频段衰减能力比较有限,不能很好地抑制并网电流中的高次谐波[16]。
而重复控制可以很好地抑制电网的各次谐波,一般根据谐波源所造成的稳态误差来分析系统的谐波抑制特性。将图3控制框图离散化后计算谐波源ug与电流误差信号ei的关系,可以得到基于单一准PR控制的并网系统的谐波抑制特性

(12)式中:P1(z)为ug到i2的传递函数。
基于准PR重复控制的系统谐波抑制特性

(13)可见,并联重复控制后,相对于单一的准比例谐振控制,系统谐波抑制特性得到了改善,改善效果主要体现在G(z)上。而且,根据G(z)的表达式可知,系统谐波抑制特性不受准PR控制器参数的影响,只需重复控制的补偿函数C(z)设计恰当,便可获得较好的谐波抑制特性。
为了满足系统的稳定条件,重复控制器参数选取必须在以P*(z)为等效控制对象的条件下保持稳定,因此,根据P*(z)的特性来设计补偿函数C(z)。
(1)Q按照工程经验可取0.95,以保证系统稳定和避免在稳态误差方面牺牲太大。
(2)由于本文选取的开关频率为10.5 kHz,基频频率为50 Hz,因而每一周期的采样次数为210,所以延时环节z-N=z-210。
(3)kr为重复控制器增益,用来幅值补偿,增大kr可使系统收敛速度加快,稳态误差减小,但系统的稳定裕度会减少。本文选取kr=0.75[17]。
(4)S(z)的设计,包括梳妆滤波器和二阶滤波器,以使S(z)P*(z)在中低频段增益为零,中高频段增益迅速衰减。
根据式(9)得等效控制对象的传递函数为:

(14)
代入各参数值并将其离散化可得P*(z)的波特图如图7所示。

图7 重复控制器的等效控制对象伯德图
从图7可以看出,P*(z)在中低频段基本具有零增益零相移的特性,不需要补偿,且在谐振频率处的幅值尖峰得到了有效抑制,可不使用梳妆滤波器。但在中高频段衰减效果不是很理想,且存在较大的相位滞后,为此,可以设计合适的二阶低通滤波器来增强系统的高频衰减特性,再通过超前环节来补偿系统总的相位滞后。
通常,二阶低通滤波器在S域的数学表达式[18]:

(15)
式中:ω为截止频率;ξ为阻尼比;本文LCL型滤波器的谐振频率为11 000 rad/s,因此确定S(s)的截止频率约为10 000 rad/s,阻尼比ξ=0.65,代入并离散化可得所设计二阶低通滤波器的传递函数为:

(16)
图8为S(z)补偿前后P*(z)的伯德图,可以看出,二阶滤波器能够增强系统在高频段的衰减能力,但自身也存在一定的相移。
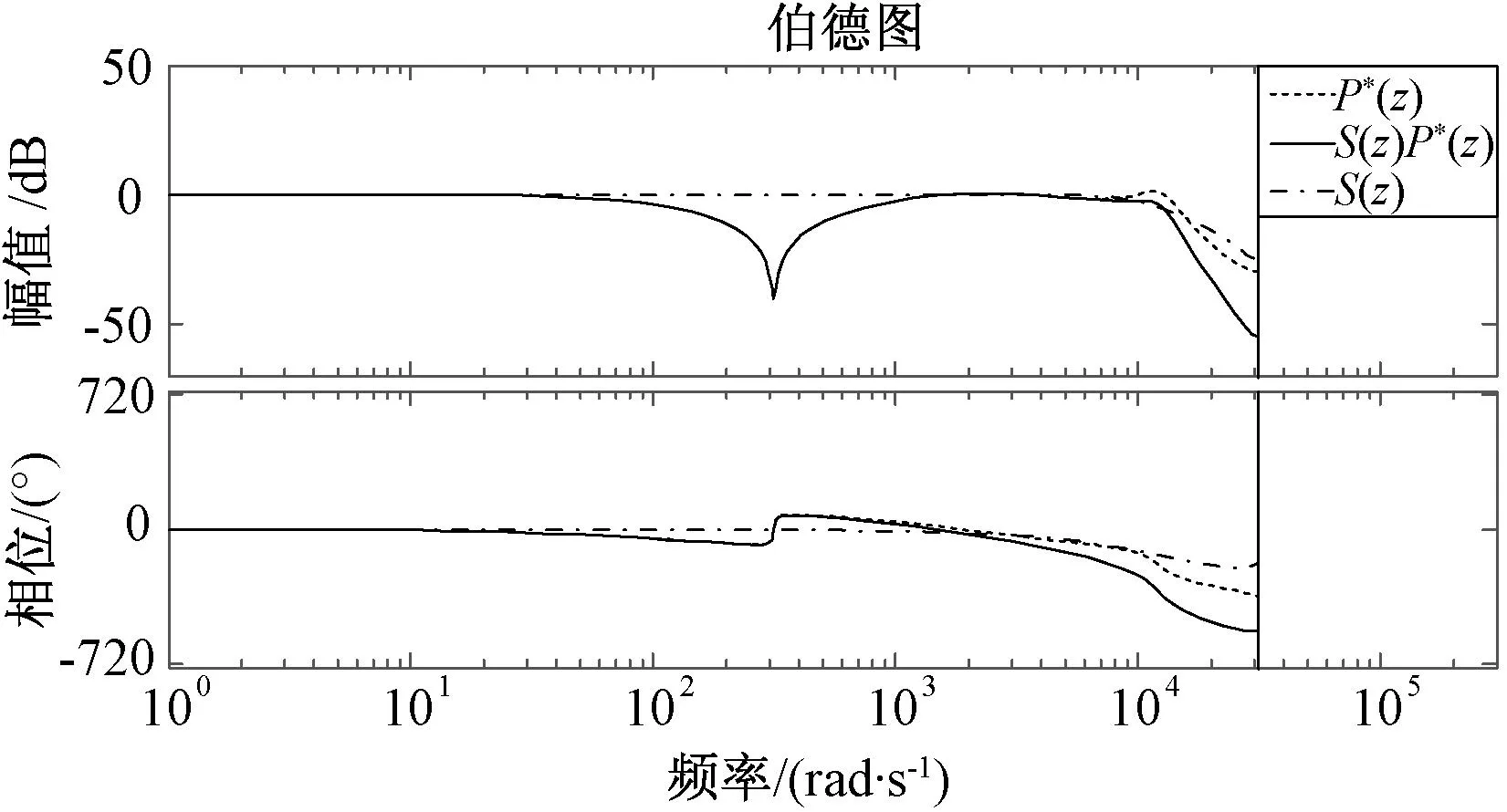
图8 S(z)补偿前后的伯德图
(5)zk为超前环节,用来补偿S(z)P*(z)引起的总相位滞后。通过实验比较得到当取k=4时,相位的补偿效果最好,如图9所示。

图9 z4S (z)补偿前后的伯德图
根据以上设计方法,得到的重复控制器的补偿环节C(z)=krzkS(z),能够保证复合控制系统的稳定性,使C(z)P*(z)在中低频段近似保持零增益和零相移特性,在中高频段增益迅速衰减,从而满足系统良好性能的要求。
4仿真分析
通过Matlab/Simulink进行仿真验证,系统参数设置如下:逆变器输出功率为3 kW,直流母线电压为400 V,电网额定相电压为220 V,额定频率为50 Hz,开关频率为10.5 kHz,直流侧LD=0.15 mH,Cdc=2 400 μF,并网侧L1=10 mH,L2=5 mH,C=1.75 μF。
图10所示为系统稳态实验波形对比,可以明显看出,采用单一准PR控制时系统达到稳态时存在工频谐波成分,而引入重复控制后,系统稳态并网电流波形得到明显改善。
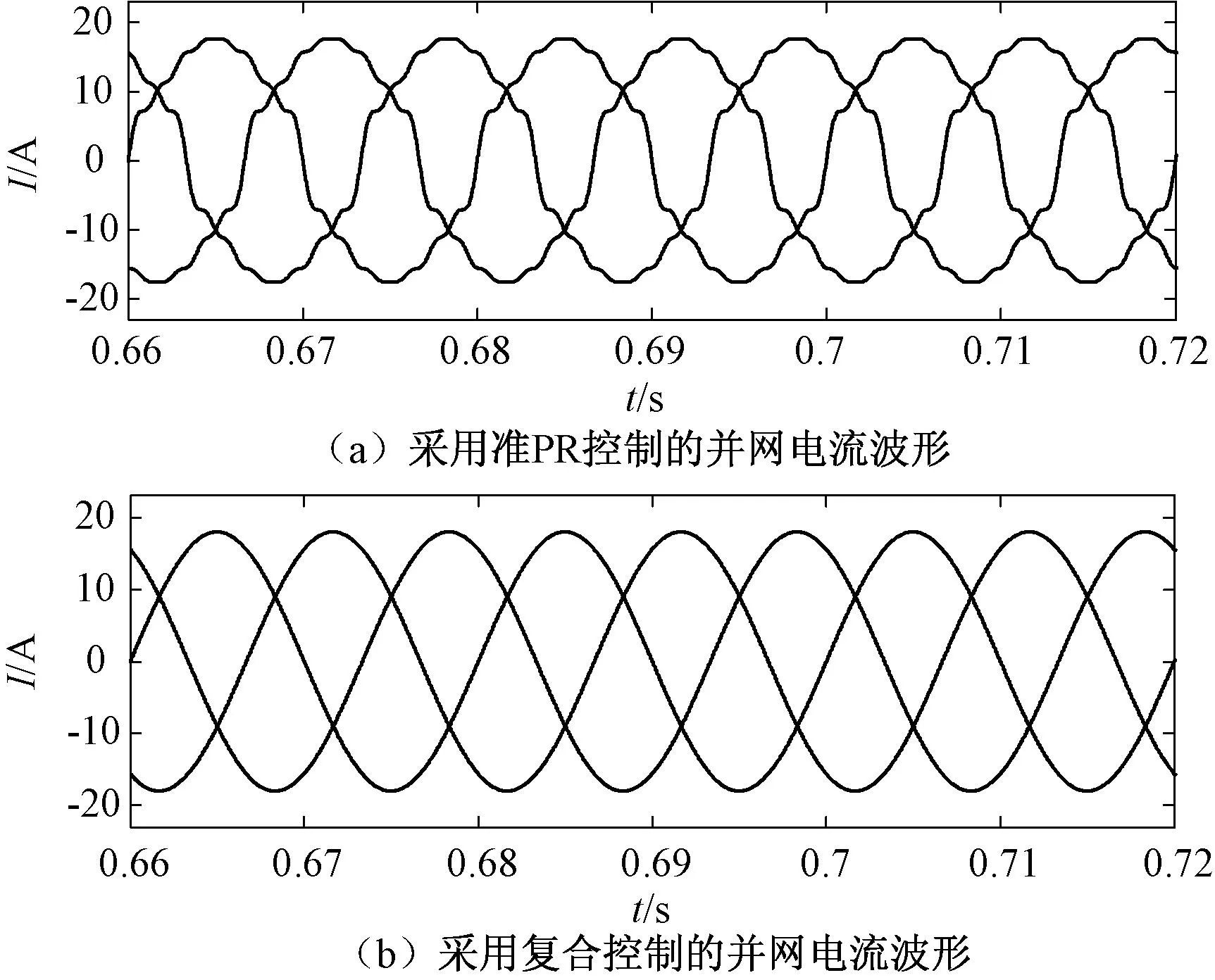
图10 系统的稳态仿真实验波形
图11所示为系统动态实验波形对比,图中在0.52 s处电流基准值从每相有效值18 A阶跃到35 A。采用单一重复控制时,动态过程较长,且在一个周期后入网电流仍有明显波动,而采用本文的复合控制后,并网电流在动态过程中迅速达到其稳态值,具有快速的动态响应能力。
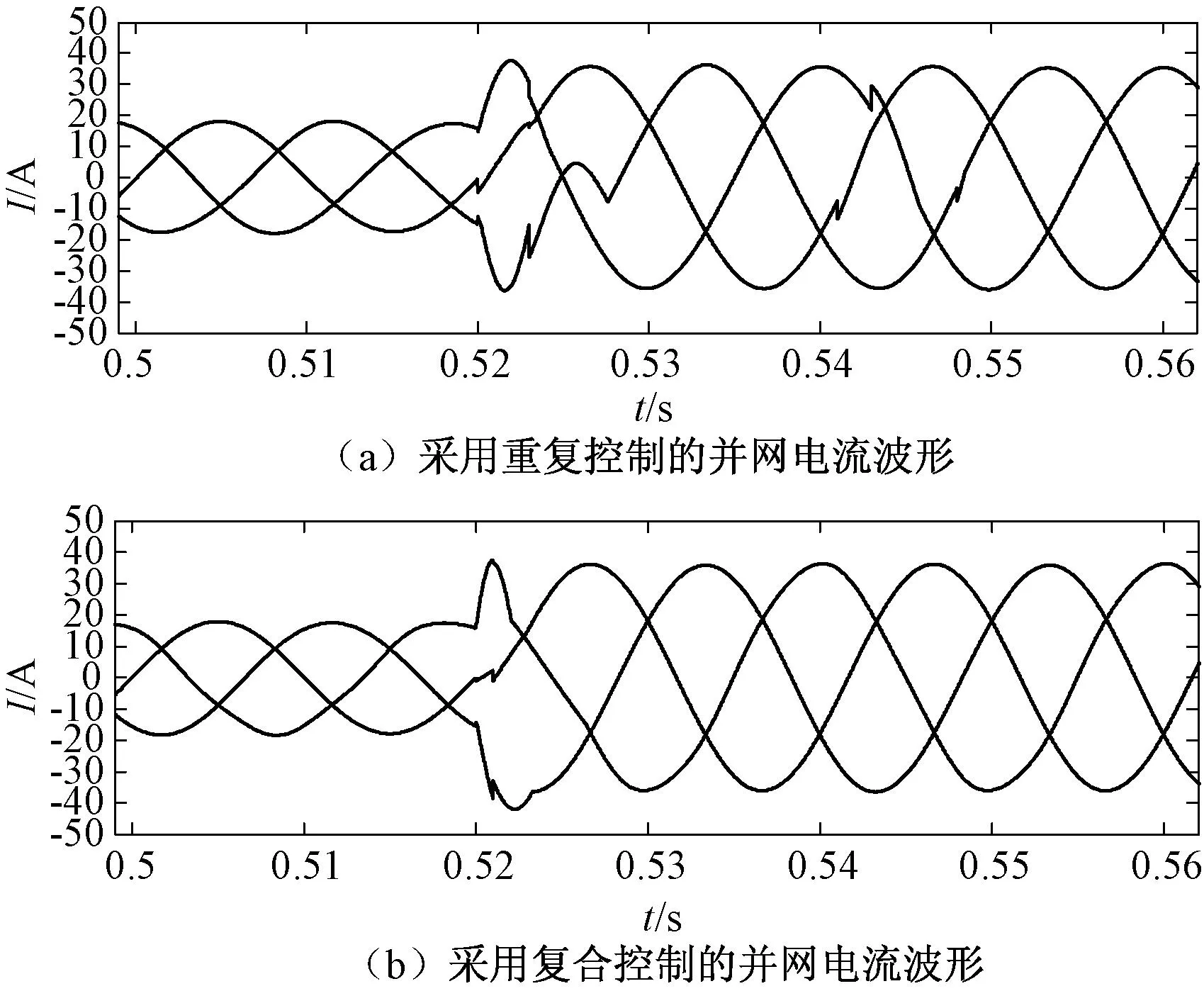
图11 系统的动态仿真实验波形
系统抗电网频率波动的实验仿真结果如图12所示,图中在0.6 s处电网频率从50 Hz突变到49.5 Hz。可以观察到,采用PI+重复控制时,并网电流波形发生了畸变,且与电网电压发生了相位偏移。而采用本文的准PR+重复控制时,并网电流几乎没有稳态误差,具有较好的抗电网频率波动能力。

图12 电网频率波动的仿真结果
5结论
本文以性能优越的LCL型并网逆变器为研究对象,提出将重复控制与准比例谐振控制相并联的复合控制策略。由仿真结果可得,准比例谐振控制能够保证系统的快速性和提高抗电网频率波动的能力,但工频谐波抑制能力差;重复控制在系统稳定后可以有效抑制各次谐波,具有良好的稳态性能,但存在动态性能差的问题,本文提出的复合控制策略能够结合两者的优点,使系统具有良好的动、稳态性能和抗干扰能力,从而改善并网逆变器的输出电流质量。
参考文献:
[1]赵为.太阳能光伏并网发电系统的研究 [D].合肥:合肥工业大学,2003.
[2]王成山,李琰,彭克.分布式电源并网逆变器典型控制方法综述 [J].电力系统及其自动化学报,2012,24 (2):15-19.
[3]Jalili K, Bernet S. Design of filters of active-front-end two-level voltage source converters [J]. IEEE Trans. on Industry Electronics, 2009, 56(5):1674-1689.
[4]Valdivia V,Pleite J,Zumel P,et al.Three phase LCL filter and transformer with integrated magnetics for grid-connected converters [C]//2008 34th Annual Conference of IEEE Industrial Electronics,2008:1027-1032.
[5]王要强,吴凤江,孙力,等.带LCL输出滤波器的并网逆变器控制策略研究 [J].中国电机工程学报,2011,31 (12):34-39.
[6]戴训江,晁勤,樊艳芳.基于阻尼谐振的光伏并网逆变器谐波补偿控制 [J].电力自动化设备,2011,31 (1):79-94.
[7]张兴,汪杨俊,余畅舟,等.采用PI+重复控制的并网逆变器控制耦合机理及其抑制策略 [J].中国电机工程学报,2014,34(30):5287-5295.
[8]梁利民,粟时平,朱镜儒.基于三相光伏并网系统的比例谐振重复控制研究 [J].电力科学与工程,2014,30(6):66-72.
[9]Chen Dong,Zhang Junming,Qian Zhaoming. An improved repetitive control scheme for grid-connected inverter with frequency-adaptive capability[J]. Industrial Electronics IEEE, IEEE Trans on,2013,60(2):814-823.
[10]刘晓庆,张代润,谭波.基于PR控制和谐波补偿的三相光伏并网系统 [J].可再生能源,2012,30 (1):9-10.
[11]李翠艳,张东纯,庄显义.重复控制综述 [J].电机与控制学报,2005,9 (1):37-44.
[12]陈宏.基于重复控制理论的逆变电源控制技术研究 [D].南京:南京航空航天大学,2003.
[13]Hamed Nazifi, Ahmad Radan.Current control assisted and non-ideal proportional-resonant voltage controller for four-leg three-Phase inverters with time-variant loads [C]//Power Electronics, Drive Systems & Technologies Conference (PEDSTC), 2013 4th IEEE, 356-357.
[14]王斯然,吕征宇.LCL型并网逆变器中重复控制方法研究 [J].中国电机工程学报,2010,30(27):69-75.
[15]许津铭,谢少军,唐婷.基于极点配置的LCL滤波并网逆变器电流控制策略 [J].电力系统自动化,2014,38(3):94-100,105.
[16]朱昊,韦钢,陈秋南,等.分布式电源单相并网逆变器控制方法研究 [J].电力科学与工程,2013,29 (9):6-12.
[17]黄挚雄,徐保友,沈玲菲,等.LCL并网逆变器新型电流双闭环控制策略研究 [J].电力系统保护与控制,2012,40(17):1-5.
[18]陈东.并网逆变器系统中的重复控制技术及其应用研究[D].杭州:浙江大学,2012.
Research on Repetitive Control Parallel with Quasi-PR of the Three-phase Photovoltaic Grid-connected Inverter with LCL Filter
Deng Yuen1, Su Shiping1, Liu Guiying1, Yang An1, Gui Yongguang2, Yan Yifan3(1. Hunan Province Higher Education Key Laboratory of Power System Safety Operation and Control,Changsha University of Science and Technology,Changsha 410114,China;2. Suqian Power Supply Company, State Grid Jiangsu Electric Power Company, Suqian 223800, China;3. Maintenance Company, State Grid Hunan Electrical Power Company,Changsha 410114,China)

