FS算法在多类型分布式电源规划中的应用

戴　伟， 王　进

(长沙理工大学 电气与信息工程学院，湖南长沙410114)

FS算法在多类型分布式电源规划中的应用

戴伟， 王进

(长沙理工大学 电气与信息工程学院，湖南长沙410114)

摘要：针对多类型分布式电源(DG)接入配电网的合理选择以及配置问题，且充分发挥DG潜在的环境效益，建立了DG总的发电成本，有功损耗和静态电压稳定裕度的多目标规划模型，并提出一种改进的多目标自由搜索算法(IMOFS)。该算法根据进化的时期自适应调整搜索半径和搜索步来提高算法性能，并且基于综合适应度机制更新个体搜索起点，提高搜索速度。为了获取分布更加均匀的Pareto前端，采用自适应网格法对非支配解集进行维护，从而提供良好的候选方案。算例结果表明：算法能够很好地协调各目标之间的相关性，验证了模型的合理性和算法的有效性。

关键词：分布式电源；环境效益；多目标自由搜索算法；搜索半径；综合适应度

中图分类号:TM715

文献标识码:A

DOI:10.3969/j.issn.1672-0792.2015.10.006

收稿日期：2015-07-23。

作者简介：戴伟(1989-)，男，硕士研究生，研究方向为分布式电源优化，E-mail：523885644@qq.com。

Abstract：Aiming at the problems of reasonable selection and configuration of multi-type distributed generators (DG) connected to the distribution network, and giving full play to the potential environmental benefits of DG, a multi-objective programming model, which entails the total generation cost of DG，the active power loss and static voltage stability indices is established, with the improved multi-objective free search algorithm (IMOFS) proposed. The algorithm improves its performance by dynamically adjusting the search radius and the search steps according to the period of evolution, and its speed by updating the individual search starting point based on the comprehensive fitness mechanism. In order to obtain the Pareto front more evenly, the adaptive grid method is adopted to maintain the non-dominated solution set, thus providing a good candidate. The results show that the algorithm can coordinate well the relationship among various objectives, and verify the rationality of the model and the effectiveness of the algorithm.

Keywords：distributed generator；environmental benefit；multi-objective free search algorithm；search radius；comprehensive fitness

0引言

随着环境问题日益突出以及化石能源的逐渐枯竭、节能环保、可靠性高、发电灵活的分布式电源(DG)受到人们越来越多的研究和利用。分布式电源并入电网，一方面可以带来巨大的环境效益与经济效益，而另一方面，接入位置与容量不当，不仅难以发挥其潜在优势，还会降低电网运行的可靠性。因此，对分布式电源进行合理的规划显得极其重要。

针对多类型DG接入配电网的优化配置问题，主要通过采取合理的优化模型以及优化方法来解决。目前，国内外学者对此进行了深入的研究，但很多仍存在考虑上的欠缺或方法上的局限性。文献[1]以最小化网络损耗为目标函数来获取规划方案。文献[2]建立了DG发电的多目标模型，采用模糊优化理论将多目标转化成单目标函数，考虑了多方面因素，综合性强，但不能得到完整的Pareto解集。文献[3]采用一种混合免疫克隆算法和粒子群算法的方法对分布式电源选址定容进行优化，两种算法分别用于维持抗体多样性和提高全局收敛速度，提高了算法全局搜索能力，却未考虑DG的环境效益；文献[3]在DG个数、单个容量和位置不确定的条件下，建立了多目标优化模型，通过归一化和加权的方法优化多目标问题，并利用遗传算法确定DG的位置与容量。算法上容易陷入局部最优；文献[4]从DG环境效益出发，以污染气体排放量、发电费用和电压偏差为多目标函数，采用粒子群算法进行求解，并用自适应网格法对已获得的Pareto解集进行维护。该文献很合理地处理了各目标之间的相关性。

鉴于以上的优点以及不足，本文基于DG环境效益以及系统稳定的考虑，建立了DG总的发电成本，有功损耗和静态电压稳定指标的多目标规划模型，采用多目标自由搜索算法对模型进行求解，并且利用自适应网格法对非支配解集进行维护，从而为规划者提供优质的候选方案。

1多类型DG规划的数学模型

1.1　分布式电源发电成本

DG接入配电网后总的发电成本C包括DG的安装投资及运行维护成本、燃料成本和环境污染赔偿成本。

(1)DG的安装投资及运行维护成本CDG为：

(1)

式中：r为折现率，取10%；CDG.i，PDG.i和KDG.i分别为第i种DG的安装成本(单位容量)、接入容量和平均容量系数；COM.i为第i种DG的运行维护成本系数[5]。

(2)燃料费用Cf。文中考虑的DG中光伏发电、风力发电和储能电池三者燃料成本和环境成本都为零；只有微型燃气轮机具有燃料成本。

(2)

式中：Cunit为微型燃气轮机每小时燃料费用；GMT.i为第i节点处微型燃气轮机出力。NMT为微型燃气轮机的待选节点集合。

(3)在系统中，只有微型燃气轮机会产生污染气体，文中只考虑CO2和NOx两大类，因此环境污染赔偿成本[6]Ce为：

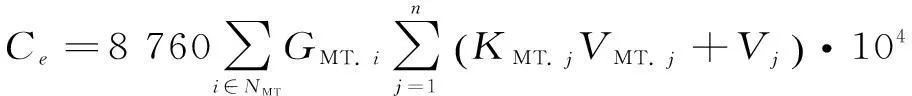
(3)

式中：n为污染气体的种类；KMT.i，VMT.i分别为第i种气体的排放强度和环境价值；Vj为排放第i种气体所受罚款。

因此发电成本C表示为：

(4)

1.2　网络损耗

DG合理的接入有利于降低配电网有功损耗，提高能源利用率。本文以系统一年平均每小时的网损为目标函数：

(5)

式中：m为网络支路总数；Ii为第i条支路上的电流；Ri为第i条支路的电阻。

1.3　静态电压稳定裕度

DG接入配电网之后能加强系统静态电压稳定性，支路的电压稳定指标为：

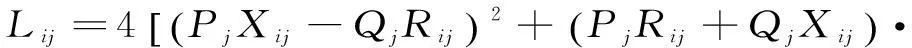
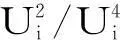
(6)

式中：Lij，Rij，Xij为支路ij的电压稳定指标、电阻、电抗；Pj和Qj分别为流入支路末端节点j的有功功率和无功功率；Ui为首端节点i的电压。

L为整个配电网支路的静态电压稳定指标，即：

(7)

式中：N为系统总支路数。则配电网的静态电压稳定裕度K为：

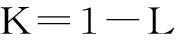
(8)

1.4　约束条件

(1)节点功率平衡约束。式(9)中Pj，Qj，Ui必须满足节点潮流方程的等式约束条件

(9)

(2)DG最大安装容量约束

(10)

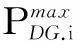
(3)节点电压约束

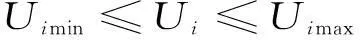
(11)

式中：Uimin，Uimax分别为第i个节点的最大允许电压值和最小允许电压值。

2多目标自由搜索算法

自由搜索算法是一种新型的群智能进化算法，具有自适应强、搜索范围广、收敛精度高等特性，为此，本文将其加以改进并拓展到多目标问题上的求解，用于解决上述的多目标模型。多目标问题与单目标问题有所不同，通过选取最优值即可实现单目标问题的优化，而多目标优化无法使各个目标同时实现最优，因而最终得到的是一个非支配的Pareto解集，Pareto解集是对子目标进行折衷的非支配解集，求解多目标问题就是获取该非支配解集[7]。

FS算法是一种基于“以不确定对不确定,以无穷对无穷”思想的智能算法，相比传统的GA，PSO等算法，该算法利用其“自由”机制在一定程度上改善了收敛速度和搜索精度。同时也发现，基本的FS算法在全局收敛、多维空间搜索等方面仍有所不足。为克服算法以上的不足，本文采用一种自适应调整搜索空间和搜索步的策略[8]，以提高算法的全局搜索性能以及收敛速度。

2.1　基本的自由搜索算法

(1)初始化。本文采取随机值法初始化种群：

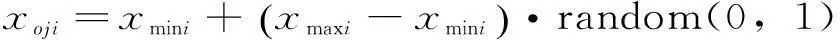
(12)

(2)寻优搜索。个体在搜索空间内进行寻优搜索，行为如下：

(13)

式中：t为搜索步中的当前小步(t=1,2,…,T);rji为第j个体在第i维变量空间搜索半径。

2.2　搜索半径和搜索步的自适应调整

搜索空间一直是决定算法精度和收敛速度的重要因素。其中，搜索半径R取值的大小决定着个体是大范围搜索还是局部寻优，而一般FS算法将R取固定值，这很容易导致算法出现长时间搜索或者提前早熟的现象。对此，本文根据个体综合适应度值采取自适应调整策略，在算法前期将个体均匀分配到搜索空间，进行全局搜索；而在后期个体已被大大的优化时，则采取局部搜索。其中，对搜索步T也进行自适应调整，则是适应R的调整，提高收敛效率。

一般的单目标问题只需找到群体中具有最大适应度的个体即可求解。而多目标优化问题得到的则是一个非支配解集，需要对种群中个体的适应度进行非劣解排序。为此，文中针对上述多目标问题提出个体适应度的确定方法，即综合适应度。

在搜索步T内个体的综合适应度[9]如下：

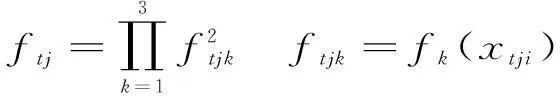
(14)

式中：k(k=1,2,3)为子目标函数；ftjk为在搜索步T内个体j的目标函数k的适应度值。

在搜索步T内的综合适应度最大值fj：

(15)

基于综合适应度机制的比例因子Fj：

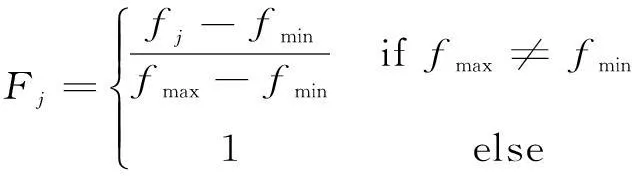
(16)

式中：fmin和fmax分别为当代个体中综合适应度的最大值和最小值。

基于比例因子进行自适应调整个体j的搜索半径Rj以及搜索步Tj公式：

(17)

(18)

式中：it为当前迭代数；IT为总迭代次数；T0为个体的初始搜索步；w是调节因子；IN取整数。

通过对R和T的调整以及两者的共同协作，适应度较好的个体加快两者的进化，并进行局部寻优；而较差的个体则减慢两者的进化，同时采取全局搜索。

2.3　个体搜索起点的更新

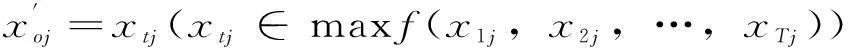
(19)

式中：xtj为具有最大综合适应度值相对应的位置。

2.4　自适应网格法

在每次迭代过程中，算法都会产生新的非支配解，而非支配解集容量是有限的，不能将这些新解都加入解集中，因此需要对非支配解集的容量加以限制，同时为了保持非支配解集中的个体均匀分布在搜索空间，本文采用自适应网格法[10]对非支配解集进行维护。网格大小不固定，在算法进化过程中，网格根据当代个体的分布情况进行动态的调整边界。

为了保证网格能够完全容纳非支配解，对于含有k个目标函数的多目标问题, 需具备2k个边界的网格，网格将目标空间划分成k维个超立方体，每一维被分割d次，目标上第k维域宽是rk，网格的边界分别为：

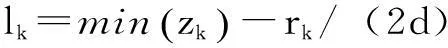
(20)

(21)

式中：lk，uk分别为网格的上界与下界；zk为子目标值。

当非支配解集的容量满溢时，则随机淘汰掉具有最大密度的超立方体中的一个个体。以保证非支配解集的更新。

2.5　算法步骤

基于IMOFS算法的多类型DG选址定容问题求解步骤如下：

(1)输入电网以及算法参数，将初始化种群随机分散到搜索空间。

(2)形成初始的非支配解集。

(3)计算出各个个体的综合适应度，并找出最大综合适应度值。

(4)根据(17)、(18)式调整个体的搜索半径和搜索步，并根据综合适应度值更新个体下一轮搜索的起点。

(5)非支配解集维护。利用自适应网格法对非支配解集进行维护和更新。

(6)判断是否满足终止条件，若是，则输出非支配解集，否则返回步骤(2)。

3算例分析

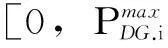
3.1　算例参数

本文采用IEEE-33节点系统进行计算，系统参数见文献[11]。该系统电压等级为12.66 kV，有功负荷为3 715.0 kW，无功负荷为2 300.0 kvar。假定单位光伏、风机、燃气轮机、储能电池的安装成本分别为4.55，1.30，0.97，1.82万/kW·h，维护成本系数分别为0.013，0.032，0.195，0.320万/kW·h。

3.2　算法性能分析

设置种群大小为40，非支配解集中个体为100，初始搜索步T0=40，最大迭代次数为150。运用NSGA-II[12]和IMOFS分别对分布式电源多目标进行求解，得到分布式电源规划模型的Pareto解集。

图1和图2反映地是分布式电源发电成本，网络损耗和静态电压指标三者之间相互制约的关系。当发电成本最小时，网络损耗和静态电压指标越大；而网络损耗和静态电压最小时，DG发电成本会越大，投资不具经济性。同时不难看出，NSGA-II的Pareto解集分布曲线出现了转折，而IMOFS所得解的分布曲线较为平滑，说明IMOFS比NSGA-II更能逼近理想的Pareto最优前沿，协调好3个函数之间的相关性。

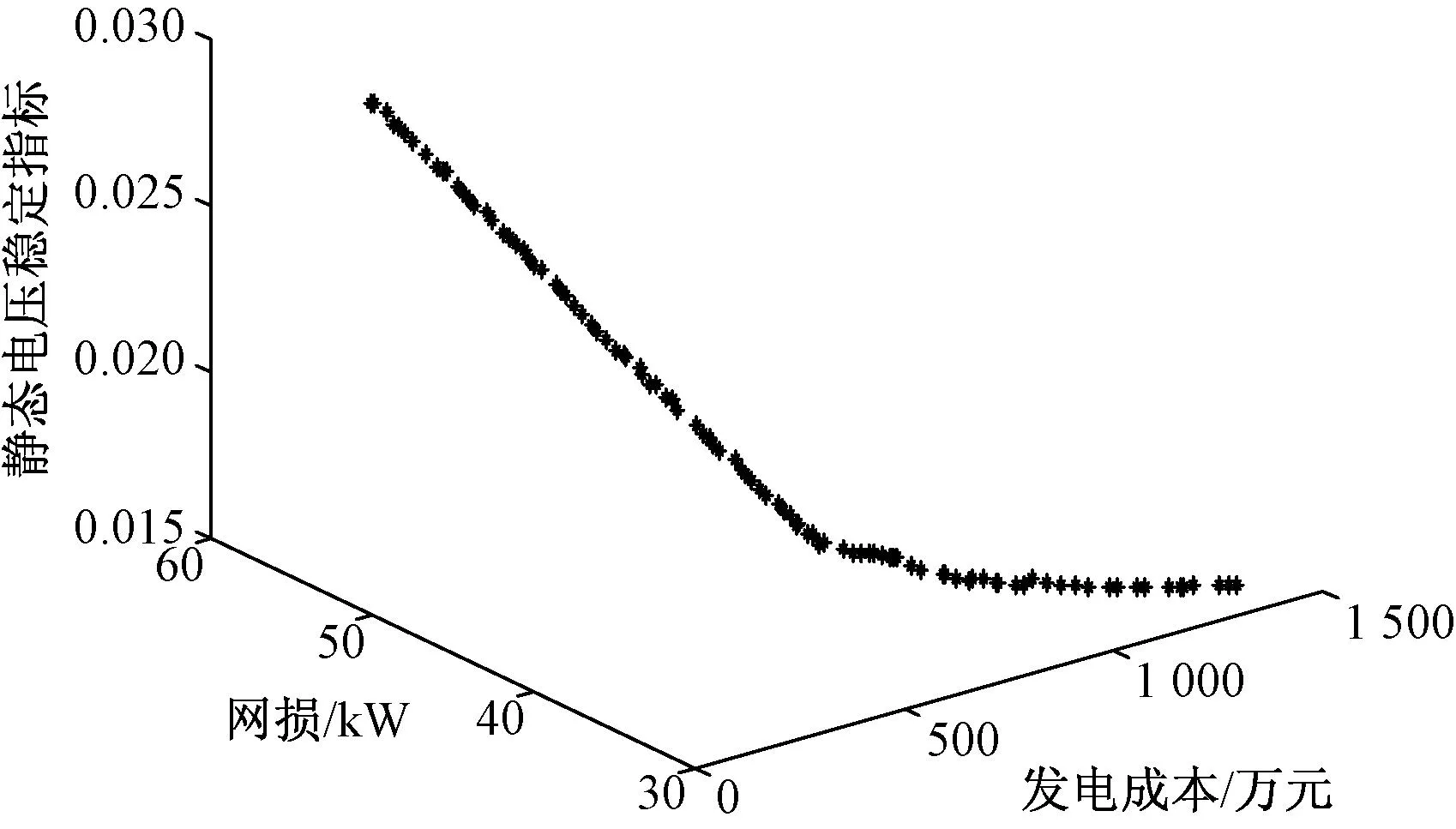
图1　NSGA-II的Pareto解集

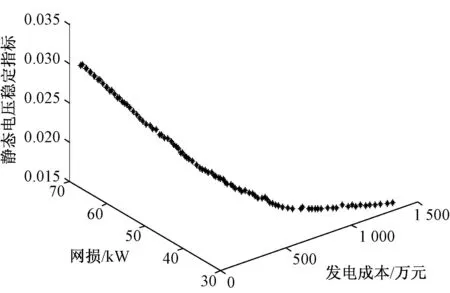
图2　IMOFS的Pareto解集

表1给出了两种算法得到的各目标值范围。可以看出IMOFS解的范围都大于NSGA-II解的范围，说明IMOFS所得的解分布更为宽广，能够提供更为全面的规划方案。

表1　两种算法得到的各目标值范围

3.3　不同配置方案分析

为研究不同配置方案3个目标函数之间的制约关系，本文选取如下4个方案进行比较。

方案1：考虑发电成本最小，即不接入DG;方案2：网损最小;方案3：静态电压指标最小；方案4：对3个目标都加以重视，采取无偏的配置方案。

由表2可以看出，方案1发电成本最小，但是网损和静态电压指标较大。比较方案2和方案3，不难看出，两者的网损和静态电压稳定指标都偏低，但发电成本较大，经济性不够。方案4采取折衷方案，3个指标都加以重视，所得到的目标函数值都较为适中。此外，IMOFS保证了Pareto最优解在Pareto前沿上的宽广性和均匀性，以及对各个目标函数之间的协调性，规划者可根据实际情况在Pareto最优解集中选择符合实际要求的DG规划方案。

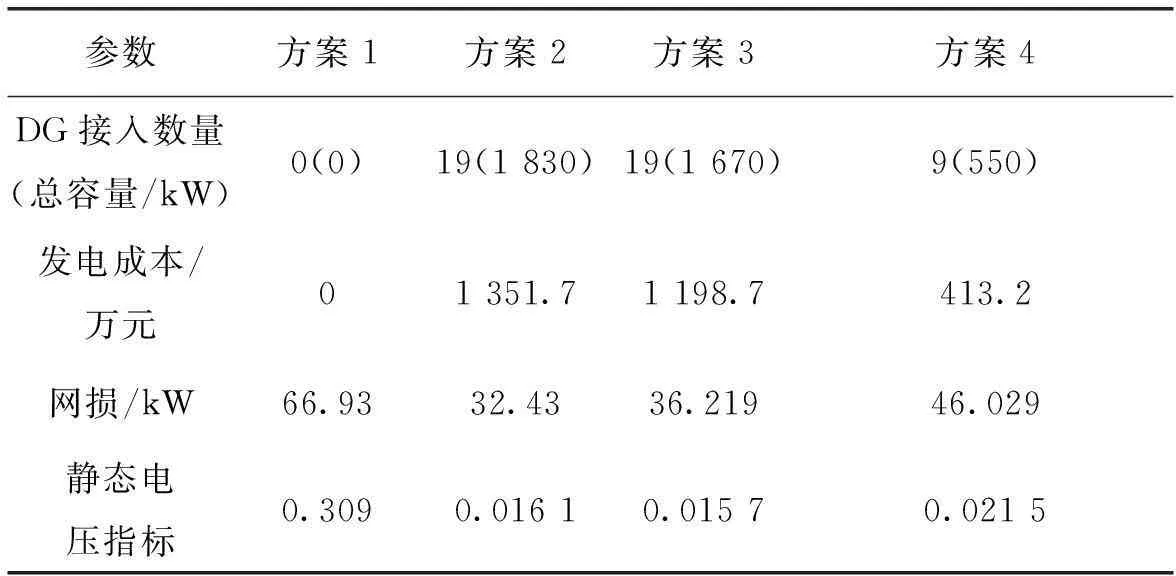
表2　DG规划方案比较

4结论

本文研究了多类型分布式电源接入配电网的优化配置问题，从经济性和系统稳定性的角度建立分布式电源规划数学模型，采用多目标自由搜索算法和自适应网格法对模型进行求解。通过算例可知：本文算法比NSGA-II算法更能协调好各目标之间的相关性，为规划人员提供更加全面的备选方案，能够在保证系统稳定和环境性的基础上，实现发电成本的最小化。

参考文献：

[1]Nara K,Yasuhiro H,Kazushige I,et al. Application of tabu search to optimal placement of distributed generators[C]//Power Engineering Sociey Winter Meeting, 2001. IEEE,2001:918-923.

[2]苗雨阳,卢锦玲,朱国栋. 基于改进多目标粒子群算法的微电网并网优化调度[J]. 电力科学与工程,2012,28(7):15-20.

[3]Li R，Ma H，Wang F，et al.Game optimization theory and application in distribution system expansion planning, including distributed generation[J]. Energies，2013，6(2)：1101-1124.

[4]栗然，申雪，钟超，等.考虑环境效益的分布式电源多目标规划[J].电网技术，2014,38(6):1471-1478.

[5]杨秀,陈洁,朱兰,等. 基于经济调度的微网储能优化配置[J]. 电力系统保护与控制,2013,41(1):53-60.

[6]于青,刘刚,刘自发. 基于量子微分进化算法的分布式电源多目标优化规划[J]. 电力系统保护与控制,2013,41(14):66-72.

[7]格玛，周晖，陆拥俊. 基于混合策略的多目标自由搜索算法[J]. 系统工程,2011,29(3):121-126.

[8]李团结，曹玉岩，孙国鼎. 动态改变邻域空间和搜索步的自由搜索算法[J]. 西安电子科技大学学报(自然科学版)，2010,37(4):737-742.

[9]刘柏良，黄学良，李军，等. 含分布式电源及电动汽车充电站的配电网多目标规划研究[J]. 电网技术,2015,39(2):450-456.

[10]Das A, Gope D. Adaptive mesh refinement for fast convergence of EFIE-based 3-D extraction [J]. Components Packaging and Manufacturing Technology IEEE Transactions on, 2015, 5(3): 404-414.

[11]邓桂秀,江修波,蔡金锭. 基于混沌二进制粒子群算法的配电网重构研究[J]. 电力科学与工程,2013,29(9):34-37.

[12]Deb K, Pratab A, Agarwal S,et al.A fast and elitist multi-objective genetic algorithm: NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182 -197.

The Application of Free Search Algorithm in Multi-type Distributed Generators Planning

Dai Wei, Wang Jin(College of Electrical and Information Engineering，Changsha University of Science and Technology， Changsha 410114，China)