指数型分布粗糙地面宽带后向电磁散射的FDTD研究

武剑,任新成,朱小敏

(延安大学物理与电子信息学院，陕西 延安 716000)



指数型分布粗糙地面宽带后向电磁散射的FDTD研究

武剑,任新成,朱小敏

(延安大学物理与电子信息学院，陕西 延安 716000)

摘要：采用蒙特卡罗方法模拟生成指数型分布粗糙地面，运用时域有限差分方法(FDTD)研究了高斯脉冲波入射时粗糙地面的宽带电磁散射问题。通过数值计算得到不同频率响应对应的后向散射系数，分析了粗糙地面相关长度、高度起伏均方根、土壤湿度和入射角的变化对后向散射系数的影响，得到了指数型分布粗糙地面的宽带后向电磁散射特性。

关键词：电磁散射；FDTD； 粗糙地面；后向散射系数；高斯脉冲波

随着无线通信技术的不断发展，随机粗糙面电磁散射问题日渐成为至关重要的研究课题，广泛应用于微波遥感、风场反演和超宽带雷达探测等诸多领域。目前，单频电磁波入射粗糙面时的电磁散射问题的研究已经取得了一些进展，任新成等[1]在粗糙地面与上方目标复合电磁散射研究中，利用时谐场源入射并外推至远区场；张连波等[2]应用矩量法，采用脉冲基函数结合点匹配技术研究了三层粗糙面的散射系数；Wang等[3]用混合方法研究了粗糙面与上方目标的复合电磁散射特性；Sultan-Salem等[4]利用基尔霍夫近似研究了分形粗糙面的电磁散射特性。对于脉冲波入射时的粗糙面宽带(超宽带)电磁散射问题的研究则相对较少[5-6]。但是，实际上粗糙面宽带电磁散射对于超宽带雷达目标成像、丛林透视和低雷达截面(RCS)目标探测的研究[7]，以及超宽带无线通信技术的发展[8]等都具有重要的借鉴意义和实用价值。

粗糙面宽带电磁散射问题传统上是通过近似解析方法进行研究的。但是，近似解析方法大多限于求解单次散射，实现起来较为简单，但有一定的适用范围。随着研究的进一步深入，矩量法[2]、前后向迭代算法[9]、有限元法[10]和时域有限差分方法(FDTD)[11]等数值算法得到快速发展。FDTD由Yee于1966年首次提出[12-13]，与其他数值方法相比，不仅能节省计算机内存，而且具有CPU占用时间短、计算效率高等优点，因此受到广泛的关注。

本文采用指数型分布粗糙面模拟实际地面，地面土壤介电常数利用Wang等[14]的四成分模型，运用FDTD方法对高斯脉冲波入射下的粗糙地面进行时域散射研究，所得散射场数据由瞬态场外推后再经傅里叶变换获得频域信息，得到后向散射系数随频率的变化曲线，分析了粗糙地面相关长度、高度起伏均方根，土壤湿度和入射角的变化对后向散射系数的影响，得到了指数型分布粗糙地面的宽带后向电磁散射特性。

1粗糙地面模拟与散射模型

1.1粗糙地面模拟

在自然界中，实际地物表面、海面均可看作是二维随机粗糙面。为了便于研究，可以将坐标系中一个方向变化另一个方向不变的二维模型简化为一维模型。对于一维粗糙面的研究，同样具有理论意义和实际意义。

用蒙特卡罗方法可以模拟生成一维随机粗糙面[15]。蒙特卡罗方法又称线性滤波法，即在频域用功率谱对其滤波再作逆快速傅里叶变换得到粗糙面的高度起伏。长度为L的一维粗糙面可以由下式生成

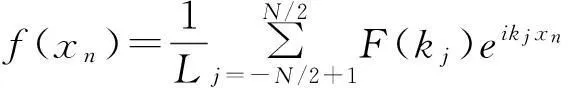
(1)

式中，xn=nΔx(n=-N/2+1,…,N/2)表示粗糙面上第n个采样点，Δx为采样间隔；kj=2πj/L，表示离散波数；F(kj)为f(xn)的傅里叶变换，可由下式计算

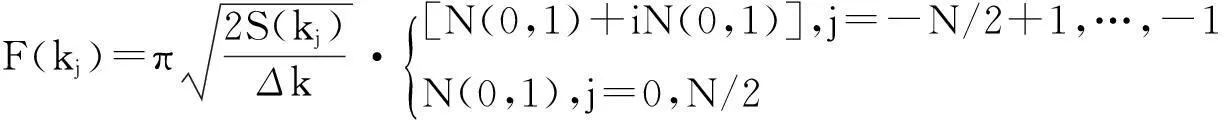
(2)

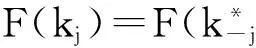
(3)

式中，δ、l分别为粗糙面高度起伏均方根、相关长度，k为波数。

1.2散射模型

图1为一维随机粗糙面电磁散射的几何示意图，粗糙面由蒙特卡罗方法模拟生成，x轴上方为自由空间，下方为均匀土壤介质。图2为粗糙面电磁散射的FDTD模型。总场边界(TF/SF边界)为平面，上方为散射场区，下方为总场区，在总场边界设置等效电磁流引入入射波，在散射场区设置输出边界，从而外推至远区散射场。在FDTD计算区域外设置厚度为10个网格的各向异性介质完全匹配层(UPML)吸收边界。

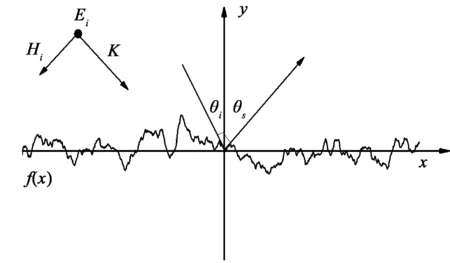
图1　一维粗糙面散射几何示意图Fig.1　　Geometry llustration of electromagnetic　scattering of 1D rough surface

图2　粗糙面散射FDTD模型Fig.2　　FDTD computation model for rough 　surface scattering

2FDTD方法

对于二维问题，电磁波分为TE波和TM波。以TE波为例，FDTD差分公式为：

(4)

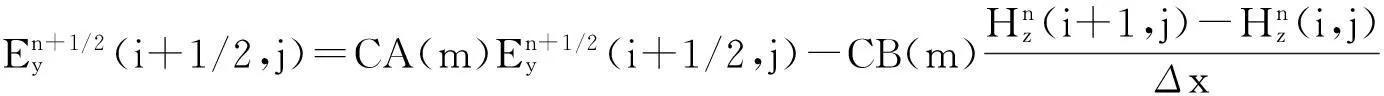
(5)

(6)

(4) ～ (6)式中CA(m)、CB(m)、CP(m)、CQ(m)及m的取值见文献[13]。Δx、Δy分别为FDTD区域x、y方向的离散网格宽度。同理，根据TE和TM波之间的对偶关系，可写出TM波的FDTD差分公式。

根据等效原理，设置等效电磁流，将入射波引入总场区，而散射场区没有入射波。文献[16]选取了微分高斯脉冲波为入射波，而本文选取高斯脉冲波为入射波，其表达式为

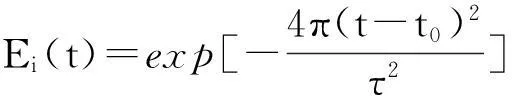
(7)

式中τ为常数，决定高斯脉冲的宽度。本文取τ=2/f，此时频谱为最大值的4.3%，选用高斯脉冲波使得t0=0.8τ时，脉冲在起始时刻近似为0。

为了解决截断边界处场值突变而产生的反射问题，普遍给入射波附加平滑高斯窗函数

G(x,y)=exp{-[(x-x0)2+(y-y0)2](cosθi/T)2},

(8)

式中θi为入射角,取x0=y0=0。τm应满足以下条件

exp[-(ρmcosθ/T)2]=10-3，

(9)

则T=ρmcosθ/2.6，ρm为中心到边缘的最小距离。

由于FDTD不能直接计算电磁散射无限区域数据，因此需在截断边界设置吸收边界条件模拟开域电磁散射过程。本文选取UPML吸收边界，取10个网格厚度。以TE波为例，各向异性介质Maxwell旋度方程表示为

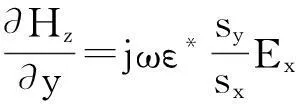
(10)

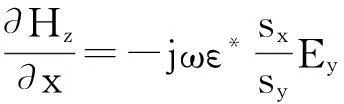
(11)

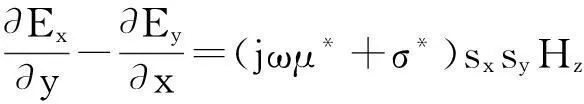
(12)

(10) ～ (12)中ε*、μ*、σ*代表与UPML层相邻内部介质的电磁参数。sx和sy分别为x和y方向的单轴参数，具体形式见文献[13]。

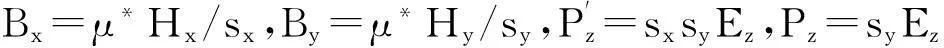
通过FDTD计算得到近场数据后，运用瞬态场外推方法可得到远区散射场，再由傅里叶变换获得远区场的频域形式。散射系数定义为

σ=10·log10(NRCS)，

(13)

单位为dB，式中NRCS表示归一化雷达散射截面，具体形式为

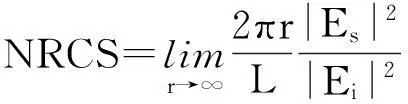
(14)

式中，r、Es、Ei分别表示观察点到原点的距离、远区散射场和入射波电场。

3数值计算结果与讨论

用上述理论和数值方法计算了指数型分布粗糙地面的后向散射系数，讨论了粗糙面相关长度、高度起伏均方根，土壤湿度以及入射角对后向散射系数的影响。具体数值计算中，选用TM极化高斯脉冲平面波作为入射波，FDTD的网格宽度为dx=0.5cm，粗糙面的抽样长度为3 200个网格，选取50个粗糙面进行统计计算。如无特殊说明，取入射角θi=30°，土壤类型选择粉沙壤土，土壤介电常数利用Wang等[14]的四成分模型进行计算。

3.1粗糙面相关长度对后向散射系数的影响

图3为后向散射系数σ随粗糙面相关长度l的变化关系。其中粗糙面高度起伏均方根δ=2cm，土壤介电常数εr=9.968 2-i3.055 6(土壤湿度取mv=0.2g/cm3)。由图3可知，当入射波频率f<75MHz时，后向散射系数σ先在较小的一个频域内迅速增大，接着急剧减小，在75MHz附近取极小值，并且极小值随着l的增大而增大，与文献[16]相比，取得极小值的频率位置略小于微分高斯脉冲波作为入射源时的频率位置；当75375MHz时，σ随f的增大振荡地缓慢变化，且σ随l的增大而减小，不同相关长度对应的σ相差不大。总之，在不同频率范围内，粗糙面相关长度对散射系数的影响不同。

图3　粗糙面相关长度对后向散射系数的影响Fig.3Impact of rough surface correlation length on backward scattering coefficient σ

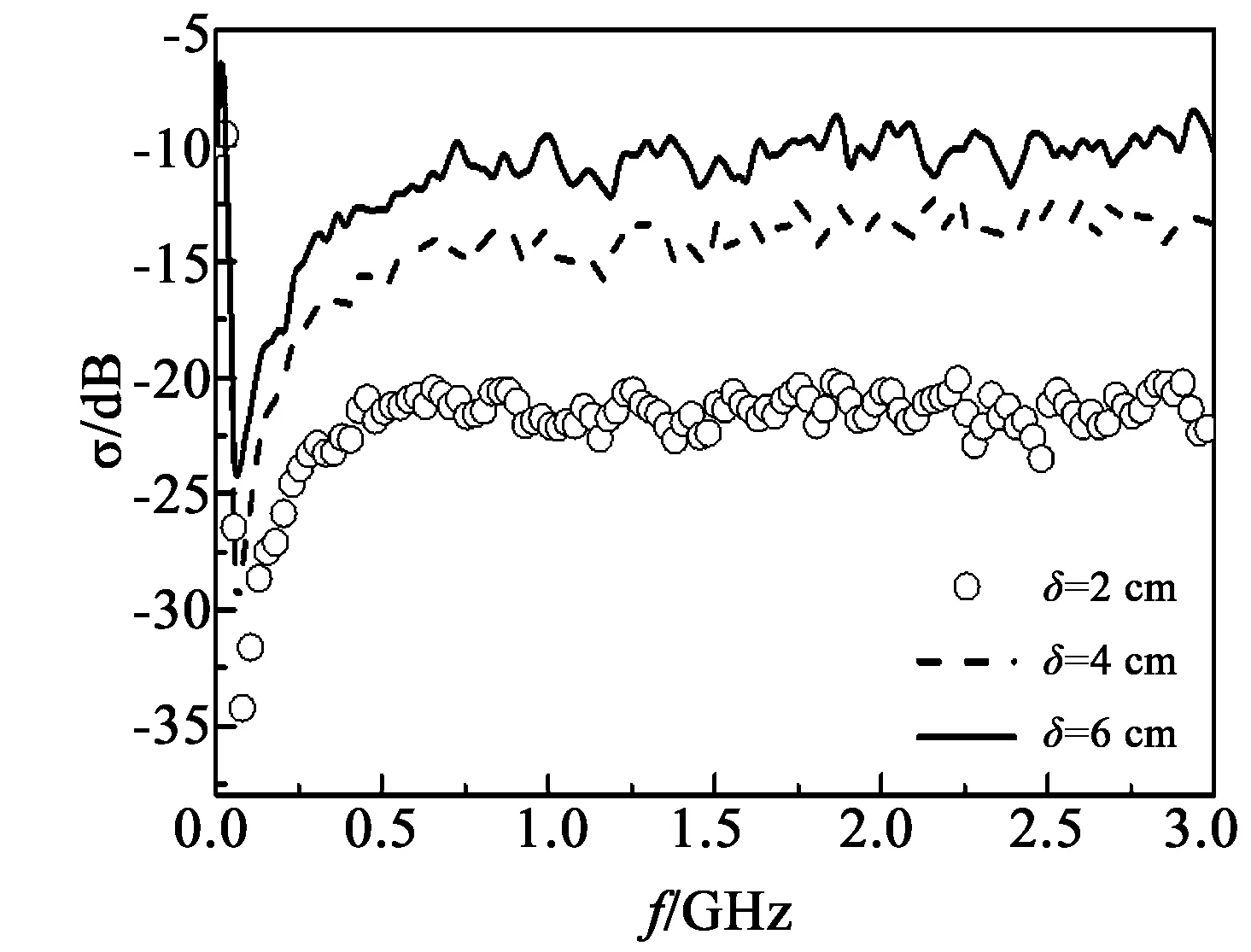
图4　粗糙面均方根对后向散射系数的影响Fig.4Impact of height RMS of rough surface on backward scattering coefficient σ

3.2粗糙面高度起伏均方根对后向散射系数的影响

图4为后向散射系数σ随粗糙面高度起伏均方根δ的变化关系图。计算中相关长度l=20cm，土壤介电常数εr=9.968 2-i3.055 6(土壤湿度mv=0.2g/cm3)。由图4可知，当入射波频率f<65MHz时，后向散射系数σ先在较小的一个频域内迅速增大，接着急剧减小，在65MHz附近取极小值，并且极小值随着δ的增大而增大；当65500MHz时，σ随f的增大振荡地缓慢变化，且σ随δ的增大而增大，同一频率不同δ对应的σ相差较大。经分析，由于粗糙面高度起伏均方根增大，粗糙面粗糙度增大，导致地面散射增强。

3.3土壤湿度对后向散射系数的影响

图5为后向散射系数σ随土壤湿度mv的变化关系图。计算过程中取δ=2cm，相关长度l=20cm，土壤介电常数根据四成分模型进行计算，即εr1=4.851 2-i0.802 7(mv1=0.1g/cm3)，εr2=9.9682-i3.0556(mv2=0.2g/cm3)，εr3=25.052 7-i9.7835(mv3=0.4g/cm3)。由图5可知，当入射波频率f<75MHz时，σ先在较小的一个频域内迅速增大，接着急剧减小，在75MHz附近取极小值，σ的极小值不随mv的变化而变化；当75500MHz时，σ随f的增大振荡地缓慢变化，且σ随mv的增大而增大，同一频率不同mv对应的σ相差不大。经分析，这是由于土壤湿度增大使得土壤介电常数的实部快速增大，而导致地表面散射增强。

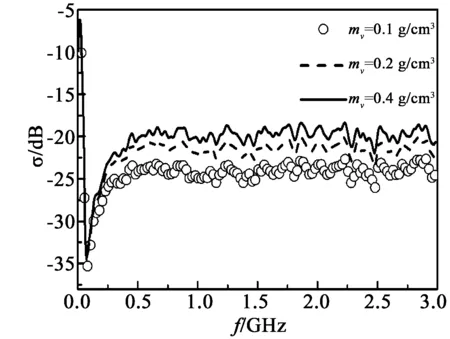
图5　土壤湿度对后向散射系数的影响Fig.5　　Impact of soil moisture on backward　scattering coefficient σ

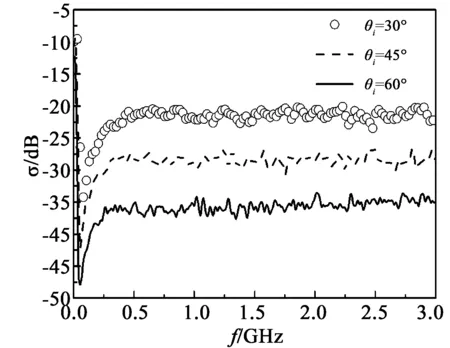
图6　入射角对后向散射系数的影响Fig.6　　Impact of incident angle on backward 　scattering coefficient σ

3.4入射角对后向散射系数的影响

图6为后向散射系数σ随入射角θi的变化关系。其中取δ=2cm，l=20cm，土壤介电常数εr=9.968 2-i3.055 6(mv=0.2g/cm3)。由图6可知，当入射波频率f<55MHz时，后向散射系数σ先在较小的一个频域内迅速增大，接着急剧减小，在55MHz附近取极小值，并且极小值随着θi的增大而减小；当55500MHz时，σ随f的增大振荡地缓慢变化，且σ随θi的增大而减小，同一频率不同θi对应的σ相差较大。总之，入射角越大，地面散射越弱。

4结语

本文研究了高斯脉冲波入射指数型分布粗糙地面的宽带电磁散射特性，运用FDTD瞬态场外推的方法进行研究，得出了粗糙地面高度起伏相关长度、均方根、土壤湿度及入射角等参数对后向散射系数的影响规律，结果表明后向散射系数随各参数变化的规律比较明显，但比较复杂；入射波波源不同，使得后向散射系数取得极值时的频率位置和对应的极值也略有不同。当然，本文仅讨论了一维指数型粗糙面的宽带后向散射问题，计算结果还有待进一步的实验验证，对于其他分布的一维地物表面、二维地物表面等的前向散射问题还有待今后进一步地研究。

参考文献：

[1]任新成，郭立新，焦永昌.雪层覆盖的粗糙地面与上方矩形截面柱复合电磁散射的时域有限差分方法研究[J].物理学报，2012,61(14):144101.

[2]张连波，郭立新，苟雪银，等.三层粗糙面电磁散射的矩量法研究[J].西安电子科技大学学报：自然科学版，2013,40(6):147-154.

[3]WANGR,GUOLX,MAJ.Hybridmethodforinvestigationofelectromagneticscatteringfromconductingtargetabovetherandomlyroughsurface[J].ChinesePhysicsB，2009,18(4):1503-1511.

[4]SULTAN-SALEMAK,LEONARTYLERG.Validityofthekirchhoffapproximationforelectromagneticwavescatteringfromfractalsurfaces[J].IEEEtrans.geosci.remoteSensing. 2004, 42(9):1860-1870.

[5]樊君，雷振亚，谢拥军,等.半空间目标宽带电磁散射特性的快速插值方法[J].电波科学学报，2012,27(1):84-89.

[6]黄纪军，粟毅，计科峰,等.地面复杂目标宽带电磁散射特性分析[J].微波学报，2005,21(2):8-11.

[7]曹秋生，刘贺军，马建超,等.基于超宽带雷达的丛林目标探测无人机系统分析[J].中国电子科学研究院学报，2012,7(4):351-355.

[8]魏为民，唐振军.UWB超宽带无线通信技术研究[J].计算机工程与设计，2008,29(11):2748-2750.

[9]金亚秋，李中新.结合谱积分加速法的前后向迭代法数值计算分形粗糙介质面的双站散射和透射[J].电子学报，2002,30(11):1648-1653.

[10]李杰.随机粗糙面及其与目标复合电磁散射有限元与高频方法建模研究[D].西安：西安电子科技大学，2012.

[11]朱小敏，任新成，郭立新.指数型分布粗糙地面电磁散射的FDTD研究[J].上海航天，2011,28(4):1-6.

[12]YEEKS.NumericalsolutionofinitialboundaryvalueproblemsinvolvingMaxwell’sequationinisotropicmedia[J].IEEETransactionsantennaspropagate, 1966，14(4)：302-307.

[13]葛德彪，闫玉波.电磁波时域有限差分方法[M].3版.西安：西安电子科技大学出版社，2011.

[14]WANGJR,SCHMUGGETJ.Anempiricalmodelforthecomplexdielectricpermittivityofsoilsasafunctionofwatercontent[J].IEEETransactionongeoscienceandremotesensing, 1980,18(4)：288-295.

[15]TSANGL，KONGJA，DINGKH,etal.Scatteringofelectromagneticwaves,Numericalsimulations[M].NewYork:JohnWileyandSons,2004.

[16]朱小敏，任新成. 随机粗糙地面的宽带电磁散射研究[J].河南科学，2014,32(8):1457-1461.

FDTDresearchofbroadbandbackwardelectromagneticscattering

fromexponentialdistributionroughlandsurface

WUJian,RENXin-cheng,ZHUXiao-min

(SchoolofPhysicsandElectronicsInformation,Yan'anUniversity,Yan'an716000,China)

Abstract∶We simulate exponential distribution rough land surface with Monte Carlo method.We also address wide-band electromagnetic scattering of rough land surface corresponding to Gaussian pulse incident wave by finite-difference time-domain (FDTD) method.Backward scattering coefficients of different frequency response are obtained through numerical calculation.We further analyze the influences of correlation length, root-mean-square of height fluctuation, soil moisture and incident angle variations on backward scattering coefficient.We eventually acquire wide-band backward electromagnetic scattering characteristics of exponential distribution rough land surface.

Key words∶electromagnetic scattering; FDTD; rough land surface; backward scattering coefficient; Gaussian pulse wave

中图分类号：TN011

文献标识码：A

文章编号：1002-4026(2015)04-0083-06

作者简介：武剑(1992-)，男，硕士研究生，研究方向为粗糙面电磁散射。 Email：yadxyjswj@163.com

基金项目：国家自然科学基金(61379026)；陕西省科学技术研究发展计划(工业攻关)(2014K05-61)；陕西省教育厅科研计划(14JK1830)

收稿日期：2014-11-22

DOI:10.3976/j.issn.1002-4026.2015.04.016