基于改进灰色GM(1，1)模型的高速公路路基沉降预测

刘建威，钟泽湘

(1.长沙市规划设计院有限责任公司, 湖南 长沙 410007；

2.中南大学 土木工程学院，湖南 长沙 410075)



基于改进灰色GM(1，1)模型的高速公路路基沉降预测

刘建威1，2，钟泽湘1

(1.长沙市规划设计院有限责任公司, 湖南 长沙 410007；

2.中南大学 土木工程学院，湖南 长沙 410075)

摘要:有效预测高速公路路基沉降的发展趋势，可以提高道路维修效率，降低事故发生率。根据路基沉降影响因素和特性，提出一种改进的GM(1,1)预测测算法。采用自动寻优定权的方法优化传统GM(1,1)模型的背景值，采用最小二乘法优化初值，有效克服背景值与初值选择的盲目性，并能保证较高的精度。分别对长湘高速某段和垄茶高速某段路基沉降进行预测试验，本文算法预测误差均值分别为2.12%和1.38%，方差比为0.137和0.146，精度等级达到一级。

关键词：路基沉降；改进；灰色预测

用高速公路路基沉降的监测数据对道路维修养护进行科学管理，合理配置维修资源，可降低维护成本，提高维护效率，进而可降低交通事故发生率，保障乘坐舒适度[1-2]。因而把握路基沉降的发展规律并进行预测具有十分重要的意义[3-4]。高速公路路基沉降的形成和发展通常受到地质因素，载荷因素，自然气候因素等共同影响[5-6]，这些影响因素通常无法有效量化,因此造成路基沉降趋势的随机性和复杂性[7]。国内外学者对道路路基沉降预测做了大量研究。三和雅史等[8]认为路基沉降数据服从Logistic分布，用概率分布特征值法建立了预测模型。Daniel[9]使用卡尔曼滤波方法对路基沉降监测数据进行预测分析。刘文豪等[10]采用神经网络和双曲线的混合模型对高速公路路基沉降预测建立了模型。陈善雄等[11]提出了一种路基沉降预测的三点修正指数曲线法，通过三点法修正灰色预测得指数曲线，从而提高预测精度。曾鼎文等[2]将优化重构背景值函数法用于湖南省高速公路路基沉降预测。陈亭[12]综合了神经网络法和双曲线拟合法对兰许高速软土路基沉降预测做了研究。但是，目前建立的高速公路路基沉降预测算法大多对路基沉降的影响因素没有全面考虑，或者算法冗杂不易实现，从而影响了预测精度。灰色系统理论认为，随机变量都是在一定范围内变化的灰色量，故原始数据可以作为灰色量，将原始数据进行一次累加处理，所得数据将呈一定规律变化，从而可以进行预测。这种算法可将复杂离乱的原始路基沉降监测数据进行处理成具有一定规律的序列。由于是针对沉降监测结果进行数据预测，从而避免了分析路基沉降复杂的成因，同时算法简洁清晰，可以保证一定的精度。但是，传统的灰色GM(1,1)模型本身存在一定局限性，从而对精度有所影响。本文在分析传统灰色GM(1,1)求解过程的基础之上，指出了GM(1,1)模型的不合理之处，并加以改进，使该模型达到了更高的道路路基沉降预测精度。

1GM(1，1)模型分析及其改进

X(0)={x(0)(k1),x(0)(k2)，…，x(0)(kn)}定义为一预测对象的原始数据监测采样序列，若ki-ki-1恒定，则称该序列为等间距序列。

为建立灰色预测模型，对该数据序列进行一次累加：

X(1)={x(1)(k1),x(1)(k2)，…，x(1)(kn)}

其中，

=X(1)(k-1)+X(0)(k)

(1)

那么，对X(1)可以建立白化微分方程：

(2)

其中，a和u分别为发展灰数和内生控制灰数。这个方程的解为：

(3)

i=2,3,…,n

(4)

令

Z(1)(ki)=μX(1)(ki)+(1-μ)X(1)(ki-1)

(5)

那么，Z(1)(k)称式(2)背景值；μ称权系数。

通常，μ取0.5，那么，

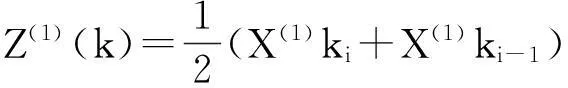
(6)

那么，式(2)的离散化形式为：

X(1)(ki)-X(1)(ki-1)+aZ(1)(ki)=u

(7)

上式的最小二乘法求解结果为

(8)

Yn=(X(0)(k1),X(0)(k2),…,X(0)(kn)T)

求得a之后则易得u。

式(3)离散化有：

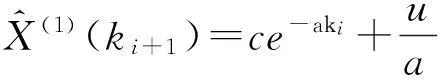
(9)

为求解常数c，需要选定一个初值，令

(10)

代入式(9)有

(11)

(12)

自此，X(0)的预测序列可全部求出。

通过分析灰色GM(1,1)模型及其求结过程，发现存在下列问题：

第一，在GM(1,1)模型中，背景值假定为一次累加序列的紧邻等权生成，即取μ=0.5。但理论上却无法证明μ=0.5时，此模型精度会达到最优。

第二，将X(0)(k1)作为求解白化微分方程的初值，即假定拟合曲线一定会过初值所在的点。但是，按照最小二乘法原理，拟合曲线却并不一定通过原始数据中的某一点，所以将原始数据中的第一点作为求解白化微分方程的初值是没有意义的。

针对以上问题，对GM(1,1)模型进行改进，流程如图1所示。

先取μ=0，代入式(7)有，

X(1)ki-X(1)(ki-1)+aX(1)(ki-1)=u

(13)

其最小二乘解：

(14)

Bu=0可由μ=0时代入式(5)求出。

(15)

最小。

图1　改进模型流程Fig.1 Process of the model improving

计算式(9)的累减式，可以得到实测序列的估计方程：

=c·(1-ea)·e-ak

(16)

令C=c(1-ea)，代入(9)式与(16)式中有：

(17)

(18)

令

将式(17)代入，有

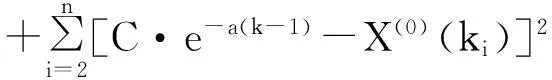
(19)

(20)

此时，这个模型的精度最高。将C代入式(17)和(18)，即可求得预测值。再用式(15)计算出在该权重下的S值。

此后，在此基础上增加一个大于0的微小增量，如以0.001为增量逐次增加直到μ=1为止。在这种情况下我们可以得到1 000个权值，取S最小者对应的权值作为最佳权值。最终以此权值作为改进GM(1，1)模型的权值。自此，最优权值和初值已全部取得。

2预测模型的精度检验

设原始序列：

X(0)(k)={x(0)(k1),x(0)(k2)，…，x(0)(kn)}

模型所生成的序列：

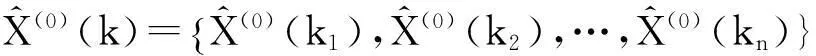
那么可以定义残差序列：

ε(0)(k)=(ε(1),ε(2),…,ε(n))

指标c越小越好，表明S1越大S2越小，表明原始数据方差大(离散程度大)而残差方差小(即离散程度小)。指标p越大越好，表明残差与残差均值之差小于给定值0.674 5S1的比较多。评价表如表1。

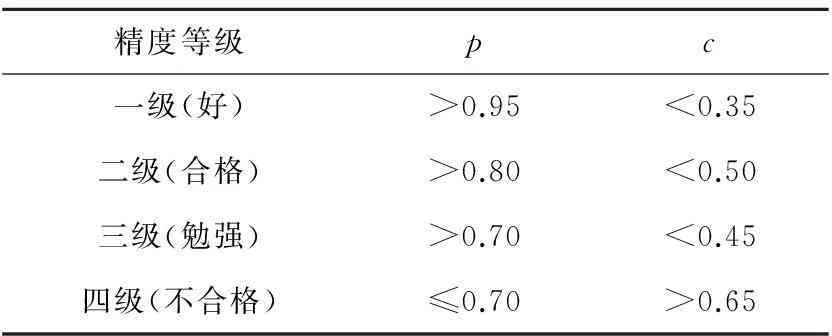
表1　精度评价表

3路基沉降预测结果算例分析

3.1　长湘高速k118+420路基沉降预测分析

以湖南省长湘高速k118+420处非等时间间隔路基沉降监测数据为例：采用YT-DG-0140单点沉降计(量程：400 mm，分辨率：0.1 mm)以沉降板法对该处路基沉降进行监测，监测试验均在天气情况良好(晴，空气湿度较小)的条件下进行，监测数据共14组，采集历时397 d，对此作为历史数据[2]进行预测,取这14个实测路基沉降值与预测值对比，如图2所示。

图2　长湘高速k118+420路基沉降预测值实测值对比Fig.2 Comparison of prediction value and measuredvalue for subgrade settlement of Changxiang expressway

表2　长湘高速k118+420处2种算法

由图2可见，本文算法所得路基沉降预测值和实际监测值相比，较好地反映了路基沉降的发展趋势。本文算法与文献[2]算法的结果比较见表2，误差均值由4.14%减少到2.12%。

3.2　垄茶高速k28+200左1.5 m处路基沉降预测分析

取垄茶高速k28+200左1.5 m处路基沉降监测数据作为历史数据[2]，同样采用沉降板法，YT-DG-0140单点沉降计对该处路基沉降进行监测，试验天气条件均良好。以共10组，采集时间为378 d，取其实测值与预测值进行对比，见图3。

由图可见，与长湘高速k118+420处类似，本算法达到了较好的预测精度。对比文献[2]的算法，见表3，相对误差均值由1.72%降低到1.38%。

图3　垄茶高速k28+200左1.5 m路基沉降预测值与实测值对比Fig.3 Comparison of prediction value and measured value for subgrade settlement of Longcha expressway

表3　垄茶高速k28+200左1.5 m处2种算法

对长湘高速k118+420处和垄茶高速k28+200左1.5 m处路基沉降的预测结果进行精度检验，检验结果见表4，精度等级达到一级。

表4　精度检验结果

4结论

1)通过构建基于背景值优化和权值选择的改进GM(1，1)模型，对高速公路路基沉降进行预测，考虑到路基沉降的发展趋势和影响因素，与之前的预测算法相比，精度有所提高。

2)基于自动寻优的思想，反复比对，提出了一种寻找最佳权值的算法。

3)对传统的GM(1,1)模型进行了改进，提出了一种优化的预测方法，对解决各领域内广泛存在预测拟问题具有一定的使用价值。

参考文献：

[1] 金亮星，李小刚.泊松曲线法在填海造地道路软基沉降预测中的应用[J].铁道科学与工程学报，2013，10(5)：52-56.

JIN Liangxing, LI Xiaogang.Application of posson curve method in the prediction of road soft foundation settlement for land reclamation[J].Journal of Railway Science and Engineering.2013，10(5)：52-56.

[2] 曾鼎文，吴浩中.优化的非等时距灰色模型在湖南高速公路路基沉降预测中的应用[J].公路工程, 2013, 38(4): 269-272.

ZENG Dingwen, WU Haozhong.Application of optimization unequal time-interval gray model in forecast of subsidence of embankment settlement of expressway[J].Highway Engineering, 2013, 38(4): 269-272.

[3] 叶观宝，司明强，赵建忠,等.高速公路路基沉的预测的新方法[J].同济大学学报，2003,31(5)：540-545.

YE Guanbao, SI Mingqiang, ZHAO Jianzhong, et al.New prediction method on final settlement on express highway[J].Journal of Tongji University, 2003, 31(5)：540-545.

[4] 杨涛，戴济群，杨伟清.基于指数法的分级填筑路堤沉降预测方法研究[J].土木工程学报，2005,38(5)：92-95.

YANG Tao, DAI Jiqun, YANG Weiqing.Settlement prediction of stage constructed embankment on soft ground using the exponent fitting method[J].China Civil Engineering Journal, 2005, 38(5)：92-95.

[5] 谷江波.高速公路软土路基沉降影响因素研究及计算分析研究[D].南京：河海大学，2005.

GU Jiangbo.Expressway soft subgrade settlement influencing factors analysis and calculation[D].Nanjing: Hehai University,2005.

[6] 周珊珊.高速公路软土路基沉降影响因素研究及灰色预测[D].北京：中国地质大学,2010。

ZHOU Shanshan.Settlement of highway soft foundation factors and prediction[D].Beijing: China University of Geosciences,2010.

[7] 单珂.高速公路路基沉降影响因素研究[J].内蒙古民族大学学报(自然科学版),2012,27(1)：37-40.

SHAN Ke.Highway embankment settlement influencing factors[J].Journal of Inner Mongolia University for Nationalities, 2012,27(1)：37-40.

[8] 三和雅史，内田雅夫．軌道状态推移モデルの设と 軌道保守施策决定法[J].鉄道研報,1996(4):7-12.

Sanwa Masashi, Vchida Masao.Setting track state trasition model and the delermining mettod of track maintenance measures[J].Rtri Report, 1996(4):7-12.

[9] Danel K.Optimal estimation and rail tracking analysis[D].Amherst: University of Massachusets,2005.

[10] 刘文豪，黎曦，胡伍生.基于神经网络和双曲线混合模型的高速公路沉降预测[J].东南大学学报(自然科学版)，2013，43(增刊)：380-383.

LIU Wenhao, LI Xi, HU Wusheng.Highway subsidence prediction based on neural network and hyperbolic hybrid model[J].Journal of southeast university (Natural science Edition), 2013,43(Suppl)：380-383.

[11] 陈善雄，王星运，许锡昌,等.路基沉降预测的三点修正法[J].岩土力学，2011,32(11)：3355-3360.

CHEN Shanxiong, WANG Xingyun, XU Xicahng et al.Three-point modified exponential curve method for predicting subgrade settlements[J].Rock and Soil Mechanics, 2011,32(11)：3355-3360.

[12] 陈亭.综合神经网络法及双曲线拟合法预测软基沉降[J].路基工程，2008(5)：151-153.

CHEN Ting.Integrated neural network and hyperbolic fitting soft ground settlement prediction[J].Subgrade, 2008(5)：151-153.

(编辑蒋学东)

Prediction of expressway subgrade settlement based on animproved gray prediction model

LIU Jianwei1，2, ZHONG Zexiang1

(1.Changsha Planning & Design Institute Co.,Ltd, Changsha 410007, China；

2.School of Givil Engineering, Gentral South University, Changsha 410075, China)

Abstract:The effective prediction of the development trend of expressway subgrade settlement can improve road maintenance efficiency and reduce the accident ratio.According to the subgrade settlement factors and features, this paper presents an improved forecasting method.The automatic optimization method was used to chose the background value and the least square theory is used to improve the initial value.In the prediction test of two examples, the results indicate that the means of the relative errors are 2.12% and 1.38%, the ratios of mean-square are 0.137 and 0.146, and the precision grade is I.

Key words：subgrade settlement; improved; gray prediction

通讯作者：刘建威(1979-)，男，湖南双峰人，高级工程师，从事道路与桥梁设计研究；E-mail：jdf199198@163.com

收稿日期：2015-04-09

中图分类号：U440

文献标志码：A

文章编号：1672-7029(2015)06-1369-05