区域网空中三角测量数据平差计算效率提升策略

胡海彦，余旭初，陈　虹，江振治，方　勇

(1. 信息工程大学地理空间信息学院,河南 郑州 450052; 2. 地理信息工程国家重点实验室,

陕西 西安 710054; 3. 西安测绘研究所,陕西 西安 710054)

HU Haiyan,YU Xuchu,CHEN Hong,JIANG Zhenzhi,FANG Yong

区域网空中三角测量数据平差计算效率提升策略

胡海彦1,2,3，余旭初1，陈虹2,3，江振治2,3，方勇2,3

(1. 信息工程大学地理空间信息学院,河南 郑州 450052; 2. 地理信息工程国家重点实验室,

陕西 西安 710054; 3. 西安测绘研究所,陕西 西安 710054)

An Efficient Computational Strategy for Aero-triangulation of Block Bundle Adjustment

HU Haiyan,YU Xuchu,CHEN Hong,JIANG Zhenzhi,FANG Yong

摘要：针对光束法空中三角测量区域网平差数值计算中计算量占比很大的法化方程组系数矩阵，提出了一种摄影区域影像片号编排下的法化方程组系数矩阵降维精简策略，可以有效降低数据处理的时间复杂度和空间复杂度，从而明显提升平差计算效率。利用实际作业数据进行了计算效率试验，与常规空中三角测量区域网数据平差相比，计算效率提高了近11倍。

引文格式： 胡海彦，余旭初，陈虹,等. 区域网空中三角测量数据平差计算效率提升策略[J].测绘通报，2015(9)：75-78.DOI:10.13474/j.cnki.11-2246.2015.0284

关键词：光束法平差；空三；线性代数；计算效率

中图分类号：P231

文献标识码：B

文章编号：0494-0911(2015)09-0075-04

收稿日期：2014-09-09

作者简介：胡海彦(1977—)，男，博士生，研究方向为航空航天高精度定位理论与方法。E-mail:173412586@qq.com

一、引言

光束法空中三角测量(简称空三)区域网平差计算属于计算密集型数据处理，如果不配合良好的算法设计和计算策略，仅靠硬件性能的提升难以满足日益增长的计算需求，在大范围区域摄影和高冗余(多基线)摄影条件下尤其如此[1]。虽然硬件性能的提升基本遵循摩尔定律，但即使性能再好的硬件，如果运行了指数级的算法(算法的时间复杂度按级别可大致分为对数级、线性级、幂数级及指数级)，当问题规模较大时，运行效率也是十分低下的，甚至出现计算崩溃的现象[2-3]。

从解析摄影测量诞生时起，围绕区域网空三数据平差处理中的计算策略或软件算法优化等方面的研究就从未停止过，有大量文献和教材可供查阅[4-5]。这些研究有的围绕独立模型法或航带法展开具体研究，其本质上是摄影区域的分区分块处理，一定程度上影响了区域平差的整体性，导致了一定的误差传递与累积[6-7]；有的就是进行“平-高”交替分求，并未有效降低问题规模，因此并不是解决计算效率提升的关键所在[8-10]。本文针对光束法整体平差求解中影响计算效率的关键点——法化方程系数矩阵，提出一种法化系数矩阵分块降维精简及摄影区域影像片号编排影响下的矩阵再精简策略，希望在解决影响光束法区域网平差计算效率的关键问题上有所突破。

二、平差计算策略

1. 分块精简法化系数矩阵

在量取同名像点坐标及控制点对应像点坐标后，空三数据平差的主要技术环节是组建观测方程组，实现途径是对共线条件方程线性化后依据最小二乘原理得到法化方程组，它是关于未知数改正量的线性方程组

NΔ=K

(1)

参考文献式中，N为法化后方程组系数矩阵；Δ为未知数改正向量；K为常数向量，矩阵中各元素的具体描述可见[11]。高效求解该线性系统的关键是法化系数矩阵N的结构分析与研究[12-13]。对于区域网平差而言，法化系数矩阵N往往特别巨大，基本策略是进行矩阵分块，以达到矩阵降维，从而减少计算时间及内存消耗的目的。

式(1)可根据外方位元素和物空间坐标两类未知数进行分块

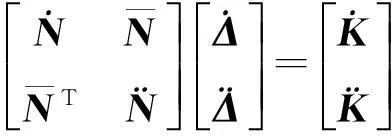
(2)

块对角矩阵在对角线方向上包含非零子矩阵，其他元素均为0，这种矩阵的最大特点是其逆矩阵也为块对角矩阵，且子矩阵为原矩阵对应子矩阵的逆[14]。因此，块对角矩阵的求逆相对其他常规非零矩阵就容易得多。基于此，可对式(2)进行重组，以便提高求解效率。首先将式(2)拆解为两组矩阵式

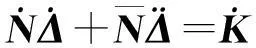
(3)

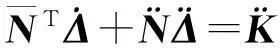
(4)

(5)

再将式(5)代入式(3)中可得

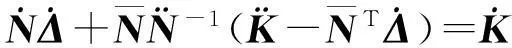
(6)

即

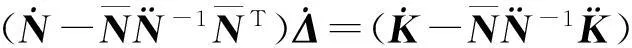
(7)

类似矩阵分块的方法同样可用于计算协方差矩阵。可将N-1分块，记为

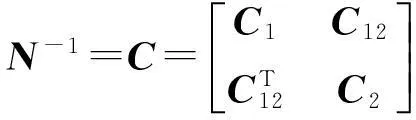
(8)

由于CN=NC=I，因此式(8)中关于矩阵C的各分块矩阵可按式(9)—式(11)求得

(9)

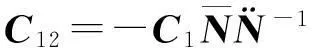
(10)

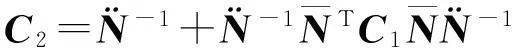
(11)

2. 像片编排次序优化

图1为一个摄影区域内3条航线(每条航线9张像片)规则摄影下的影像分布情况，航向、旁向重叠率分别为60%和30%。图中仅示意了1、2条航线的前3张像片地面覆盖状况，虚线部分为像对所对应规则立体模型排列示意。具有代表性的连接点A映射在像片1—1、1—2、1—3、2—1、2—2、2—3 6张像片上，这6张像片能够组成的可能立体像对都被A点“链接”了。整个摄影区域的影像链接(重叠)关系如图2所示，示意了整个摄影区域所有连接点形成的拓扑连接关系“图”(直线段或弧线段表示)。

这些影像链接(重叠)关系即确定了精简法化方程系数矩阵中相应位置的非零子矩阵。至于非零子矩阵在精简法化方程系数矩阵中的具体矩阵位置则是由像片号的排序方式所决定的。一般有两种排序策略—沿航线排序、跨航线排序，见表1。沿航线像片排序指先依航线序，再依像片序进行整个摄影区域的像片排序；而跨航线像片排序指先依像片序，再依航线序进行整个摄影区域的像片排序。

图1　每航线9张像片的3条航线分布

图2　关于连接点的像片间重叠拓扑关系

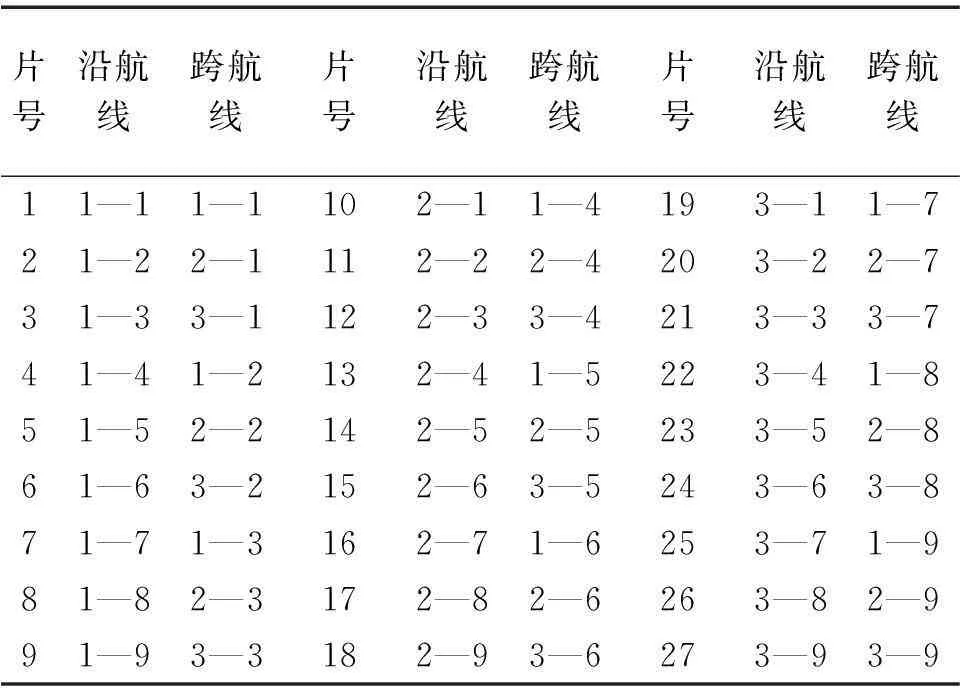
表1　沿/跨航线图1摄影区域影像排序

图3(a)为沿航线像片排序策略下的精简法化方程系数矩阵结构，非零元素趋向对角线形成带状排列。带宽为对角线到最远非零元素距离，所示矩阵的带宽为6×12=72。图3(b)为跨航线像片排序策略下的精简法化方程系数矩阵结构，其带宽为6×8=48，相比图3(a)，其带宽大大地减小了，而这对矩阵存储及解算耗时都大有益处。

根据矩阵运算操作次数分析可知，对于非带状的精简法化方程系数矩阵，线性系统的解算时间正比于未知数个数(6m)的3次方。例如，此处的27张航片的情况为解算时间正比于(6×27)3=4.2×106。对于带状矩阵，解算时间正比于带宽平方乘以未知数个数。例如，图3(a)对应的解算时间正比于722×(6×27)=8.4×105，其比非带状矩阵情况解算时间快了5倍。而图3(b)对应的解算时间正比于482×(6×27)=3.7×105，其比非带状矩阵情况解算时间快11倍多。

三、试验及分析

有关试验数据的测区情况与区域网基本参数见表2，每条航线18张影像，野外测量点69个(29个用于控制，40个用于精度检查)，采用Geolord-AT商用平差软件进行作业计算，结果见表3。

表2　区域网基本参数

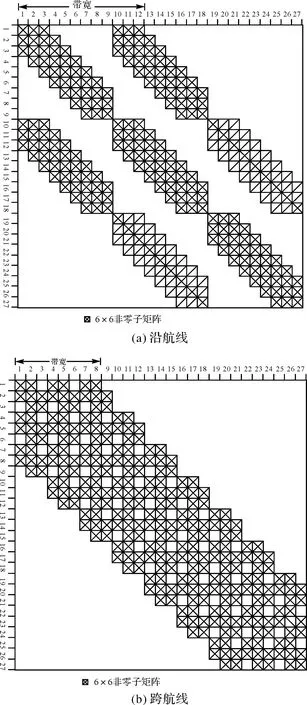
图3　沿航线、跨航线像片排序策略下的精简法化方程系数矩阵结构

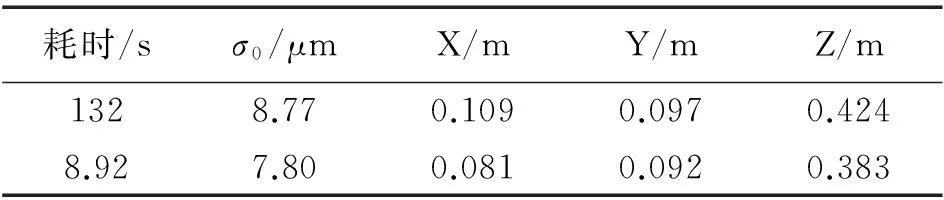
耗时/sσ0/μmX/mY/mZ/m1328.770.1090.0970.4248.927.800.0810.0920.383

为了验证本文提出的跨航线影像片号编排下的精简法化系数矩阵空三计算效率提升效果，采用以下4种试验方案进行计算效率比对，见表4。

方案1：原始法化方程组(式(1))的直接解算(片号随机编排下的暴力解)。

方案2：未考虑影像片号编排策略的非带状对角精简法化方程组解算(片号编排随机)，这是对式(7)、式(5)的直接应用。

方案3：沿航线影像片号编排下的非带状对角精简法化方程组解算，这是依据图3(a)对式(7)、式(5)的间接应用。

方案4：跨航线影像片号编排下的非带状对角精简法化方程组解算，这是依据图3(b)对式(7)、式(5)的间接应用。

根据上述4种方案，采用CLAPACK线性代数数值计算软件包，分别实现了各方案对应的4个软件模块用于数值计算效率评估，该软件包提供了可靠的矩阵基本操作和运算，并针对稀疏矩阵和带状块对角矩阵提供了专门的API函数调用。基础计算平台软硬件为：32位微软XP操作系统、2.4 GHz Pentium(R)4CPU、1GB RAM。

实际作业数据的规模为6m+3n=6×108+3×2140=7068。为了分析计算效率随问题规模大小变化的规律，在此基础上抽稀加密点个数为1070个，则问题规模减小为6×108+3×1070=3858；再利用ERDAS遥感软件以同样的匹配精度(1/3像元)再匹配加密，使得加密点个数增加到3985个，则问题规模增加到6×108+3×3985=12 603。试验过程中，同一问题规模下不同试验方案的初始值等输入条件是完全相同的。

表4　4种试验方案下的计算耗时统计　s

从表4可以看出，方案1无论是时间消耗还是空间消耗都是所有方案中最大的，计算效率最低。理论上随问题规模的增长呈幂数级时间复杂度规律，而当问题规模为12 603时，甚至出现内存溢出、程序崩溃现象。相比方案1，方案2计算耗时陡降。而且更进一步，方案3和方案4分别又比方案2计算效率提高了约5倍和11倍，与理论分析基本一致，达到了预期大幅度提高平差计算效率的目的，而且与作业单位提供的成果相比，平差精度相当，甚至还略高些(见表3)，表明本文所提出策略实现的平差软件不会额外损失平差精度。

四、结束语

法化系数矩阵的结构和规模是影响光束法区域网平差空三计算效率的最主要因素之一，针对这种情况，本文提出了一种摄影区域跨航线影像片号编排下的法化系数矩阵分块降维精简策略，通过理论分析和实际作业航摄影像数据平差试验，表明基于该策略的数据平差处理算法相比常规平差算法，在时间效率和存储效率上都有大幅度提升。这对空三数据处理相关程序算法设计与软件实现都有很好的借鉴意义，对航摄规划、影像获取及数据处理过程中的片号编排也有一定的指导作用。当然，这里的两种像片排序策略比对分析只是针对规则区域摄影进行了讨论。对于非规则摄影区域，应该研究更为适用的方法以求得最小带宽，从而节省解算时间，后续还存在更进一步的研究空间。

[1]MCGLONE J C，MIKHAIL E M，BETHEL J S，et al. Manual of Photogrammetry [M]. Maryland：American Society for Photogrammetry and Remote Sensing, 2004.

[2]SHAFFER C A. 数据结构与算法分析: C++ 版[M].北京：电子工业出版社, 2002.

[3]严蔚敏，吴伟民. 数据结构[M].北京：清华大学出版社, 1992.

[4]WOLF P，DEWITT B，WILKINSON B. Elements of Photogrammetry with Application in GIS[M]. New York: McGraw-Hill Education, 2013.

[5]EGELS Y，KASSER M. Digital Photogrammetry[M]. London: Taylor & Francis, 2010.

[6]MORGAN D，FALKNER E. Aerial Mapping: Methods and Applications[M]. London: Taylor & Francis, 2010.

[7]LUHMANN T，ROBSON S，KYLE S. Close Range Photogrammetry: Principles, Techniques and Applications[M]. Caithness:Whittles Publishing, 2006.

[8]江延川. 解析摄影测量学[M]. 郑州: 信息工程大学,2001.

[9]王树根. 摄影测量原理与应用[M]. 武汉: 武汉大学出版社, 2009.

[10]王之卓. 摄影测量原理[M]. 武汉: 武汉大学出版社, 2007.

[11]BEHAN A. Digital Photogrammetry: A Practical Course[J]. The Photogrammetric Record, 2010, 25(132): 476-477.

[12]STRANG G. Introduction to Linear Algebra[M]. Wellesley: Wellesley-Cambridge Press, 2009.

[13]DEMMEL J W. Applied Numerical Linear Algebra[M]. Philadelphia: Siam, 1997.

[14]MARCUS M. Introduction to Linear Algebra[M]. Mineola: Courier Dover Publications, 1988.

[15]FOX L. An Introduction to Numerical Linear Algebra[M]. Oxford: Clarendon Press, 1964.

[16]SEARLE S R. Matrix Algebra Useful for Statistics[M]. New York: Wiley-Interscience, 2006.

[17]SCHWERDTFEGER H. Introduction to Linear Algebra and the Theory of Matrices[M]. Groningen: P. Noordhoff, 1950.引文格式： 桂新，戴微. MASK在遥感影像水系提取中的应用[J].测绘通报，2015(9)：79-82.DOI:10.13474/j.cnki.11-2246.2015.0285