动力学中的临界极值问题探析
周春++王梅蓉

所谓临界状态,是指当某种物理现象(或物理状态)变为另一种物理现象(或物理状态)的转折状态.临界现象是“量变引起质变”的哲学思想在物理学上的生动体现,极值问题则是在满足一定的条件下,某物理量出现极大值或极小值的情况.临界问题往往是和极值问题联系在一起的.
在解决临界极值问题需注意以下几点:
(1)临界状态是一个特殊的转换状态,是物理过程发生变化的转折点,在这个转折点上,一些物理量达到极值.
(2)许多临界问题常在题目的叙述中出现“恰好”、“最大”、“至少”等词语,对临界问题给出了一定的暗示,审题时只要抓住这些特定词语的内涵规律就能找到临界条件.
(3)有的临界问题通常具有一定的隐蔽性,解题灵活性较大,审题时应力图还原习题的物理情景,抓住临界状态的特征,找到正确的解题方向.
解决动力学的临界极值问题通常有两类方法,一类是物理方法,另一类是数学方法.
一、用物理方法解临界极值问题
直接把物理问题(物理过程)推到极端,分析在极端情况下可能出现的状态和满足的条件,讨论临界状态,找出临界条件,从而求出临界值.
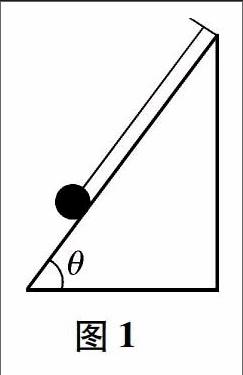
例1 一个质量为0.2kg的小球用细绳吊在倾角θ=53°的斜面顶端,如图1所示,斜面静止时,球紧靠在斜面上,绳与斜面平行,不计摩擦,当斜面以10m/s?的加速度向右做加速运动时,求绳的拉力及斜面对小球的弹力的大小.
解析当加速度a较小时,小球与斜面体一起运动,此时小球受重力m、绳的拉力T和斜面的支持力Ⅳ三个力作用,绳平行于斜面.当加速度a足够大时,小球将“飞离”斜面,此时小球只受重力和绳的拉力作用,绳与水平方向的夹角未知,题目中要求a=10m/S?时绳的拉力及斜面的支持力,必须先求出小球恰好离开斜面的临界加速度ao,此时,小球所受斜面支持力恰好为零.
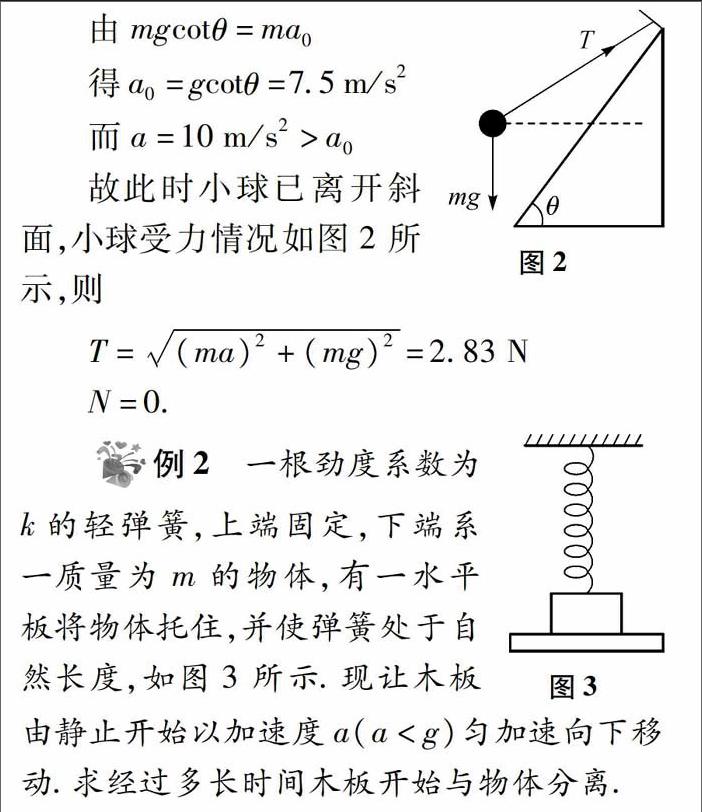
由mgcotθ=mao
得ao=gcotθ=7.5m/s?
而a=10m/S?>ao
故此时小球已离开斜面,小球受力情况如图2所示,则
例2 一根劲度系数为k的轻弹簧,上端固定,下端系一质量为m的物体,有一水平板将物体托住,并使弹簧处于自然长度,如图3所示,现让木板由静止开始以加速度a(a 解析木板与物体之间作用力恰好为零时是两者分开的临界点. 设物体与平板一起向下运动的距离为x时,物体受重力mg、弹簧的弹力kx和平板的支持力N作用. 对物体,由牛顿第二定律得: mg-kx-N=ma 当N=O时,物体与平板恰好分离,此时由上式可得: mg-kx=ma 由于木板一直做加速度为a的匀加速直线运动,则由运动学规律得: 例3如图4所示,质量为M的木板上放着一质量为m的木块,木块与木板间的动摩擦因数为μ1,木板与水平地面间的动摩擦因数为μ2.求加在木板上的水平拉力F为多大时,才能将木板从木块下抽出?设木块与木板之间的最大静摩擦力等于滑动摩擦力. 解析 M和m以摩擦力相联系,只有当二者发生相对滑动时,才有可能将M从m下抽出,因此临界状态是:M与m间的摩擦力必定是最大静摩擦力fm,且m运动的加速度必定是二者共同运动时的最大加速度am. 设此时作用于M的力为Fm,再取M、m整体为研究对象,则有 Fm-μ2(M+m)g=(M+m)am 即FFm=(μl+μ2)(M+m)g 当F>Fm,即F>(μ1+μ2)(M+m)g时,才能将木板从木块下抽出. 二、用数学方法解临界极值问题 先以物理定理、定律为依据,求出所研究问题的一般规律和一般解的形式,然后运用数学知识求极值,常用的数学方法有函数法、一元二次方程判别式法、不等式法、图象法等. 例4 如图5所示,质量为m的物体放在水平地面上,物体与地面间的动摩擦因数为μ,用大小为F的恒力使物体沿地面向右做直线运动,物体可视为质点,则怎样施力才能使物体产生最大的加速度?最大加速度为多少? 解析 设力F与水平方向夹角为a,对物体受力分析如图6所示. 对物体有 Fcos0一uN=ma N+Fsina=mg 例5 水平传送带被广泛地应用于机场和火车站,用于对旅客的行李进行安全检查.图7为一水平传送带装置示意图,绷紧的传送带AB保持某一恒定速率运行.一质量为m=4kg的行李无初速度地放在A处,设行李与传送带间的动摩擦因数μ=0.1,AB间的距离ι=2m,g取10m/S?.求行李从4处传送到B处的最短时间和传送带对应的最小运行速率. 解析 行李无初速地放在传送带上后,先在传送带的带动下做匀加速运动,当物体的速度增加到与传送带速度相等时,与传送带一起做匀速运动.行李运动的v-t图象如图8所示,图线与t轴包围的面积表示行李运动的位移大小,图8画出了行李在传送带不同的运行速度下的v-t图象.由图象可以看出,当传送带运行的速度越大,传送的时间越短,因此当行李从A处一直匀加速运动到B处时,传送时间最短, 行李刚开始运动时所受的滑动摩擦力 f=μmg 由牛顿第二定律,得 f=ma 代人数值,得a=1m/S? 得tmin=2s 传送带对应的最小运行速率 Vmin=atmin=2m/s 临界极值问题是动力学中常见而又重要的一类问题,解决这类问题,正确的受力分析是基础,准确的找到临界极值情况是关键.

