三目标混合骨干粒子群算法的电力系统无功优化

马立新，王继银，项　庆，黄阳龙

(上海理工大学 光电信息与计算机工程学院，上海200093)

三目标混合骨干粒子群算法的电力系统无功优化

马立新，王继银，项庆，黄阳龙

(上海理工大学 光电信息与计算机工程学院，上海200093)

摘要：电力系统无功优化通常以降低有功网损和减小电压偏移为目标，建立了综合考虑有功网损和电压偏移最小及电压稳定裕度最大的三目标无功优化模型。首次引入混合骨干粒子群算法用于解决电力系统无功优化问题。该算法利用关于粒子个体极值和全局极值的高斯分布对粒子位置进行更新，再通过K-均值聚类的方式，引入单纯形法对有代表性的粒子进行单纯形搜索，使算法既能够具备较强的全局搜索能力，又能够提高收敛速度和精度。将该算法和其他算法应用于IEEE-14节点系统中进行无功优化，通过数据的计算和比较，结果验证了该模型和算法用于解决多目标电力系统无功优化问题的优越性和实用性。

关键词：骨干粒子群；K-均值；单纯形；三目标优化；电压稳定裕度

中图分类号:TM714

文献标识码:��码: A

DOI:10.3969/j.issn.1672-0792.2015.11.004

收稿日期：2015-08-31。

基金项目：沪江基金(C14002)；上海市张江国家自主创新重点项目(201310-PI-B2-008)。

作者简介：马立新(1960-)，男，教授，主要研究方向为配电网规划与优化配置、电力负荷需求分析与预测方法、调速系统智能控制等，E-mail:1215750647@qq.com。

Abstract：The reactive power optimization in power system usually aimes at reducing active network losses and voltage deviation, while the currently established three-objective reactive power optimization model considers the minimization of active network losses, voltage deviation and the maximum of voltage stability margin. To solve the reactive power optimization problem, hybrid bare-bones particle swarm optimization is introduced in this essay for the first time. The algorithm employs Gaussian distribution of particle individual extremum and global extremum to update particle location. Then it introduces simple method to search for the representative particles by the way of K-mean clustering. This algorithm not only tends to have strong global search ability, but also can improve the convergence speed and accuracy. The results of calculation and data comparison justify the superiority and practicality of this model and algorithm in solving multi-objective power system reactive power optimization problem. It is superior to algorithms when they are implemented on IEEE-14 node system.

Keywords：bare-bones particle swarm optimization；K-means；simplex method；three-objective reactive power optimization；voltage stability margin

0引言

随着电力系统的完善，人们对系统运行的安全性越发重视，为了能更加明确显示电力系统电压运行点距离崩溃点的宽度[1]，本文建立了以节点电压偏移最小，有功网损最少以及电压稳定裕度最大为目标的三目标无功优化模型。

粒子群算法(Particle Swarm Optimizati- on,PSO)是一种群智能优化算法[2]。目前，标准PSO及相关改进算法用于解决RPO问题已有很多，但是由于标准PSO算法具有容易陷入局部极值，收敛速度慢等不足[3]，导致PSO算法在解决RPO问题上，未能取得很好的效果。

基于标准PSO的上述不足，本文引入了一种混合骨干粒子群算法(Simplex Method-Bare-Bones Particle Swarm Optimization,SM -BBPSO)[4],该算法是一种新兴的全局优化技术，并将其首次应用于电力系统无功优化问题。该算法是利用骨干粒子群算法对粒子的位置进行更新，通过K-均值聚类的方式对粒子分类，再引入单纯形法对各类中心粒子进行搜索，使算法既能够具备骨干粒子群算法较强的全局搜索能力，又能够由于单纯形法的引入来提高收敛速度和精度，通过对IEEE-14节点系统的仿真计算，并与标准PSO及差分进化算(Differential Evolution, DE)法进行比较，验证了本算法解决RPO问题的可行性及优越性。

1三目标无功优化模型

1.1　目标函数

本文以电压偏移和有功网损最小及电压稳定裕度最大为目标，建立优化模型。

(1)有功网损Ploss

(1)

式中：N为系统网络总支路数；δi，δj是节点i、j的电压相角；Gk(i,j)为支路k的电导；Vi，Vj是节点i、j的电压。

(2)电压偏移dv

(2)

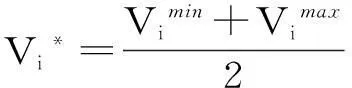
(3)静态电压稳定裕度: 以收敛潮流中雅克比矩阵的最小特征值最大化，来作为电压稳定的指标[5]。目标函数表达式如下：

(3)

式中：λmin是雅克比矩阵的最小特征值。

1.2　约束条件

(1)功率约束

保持功率平衡：

(4)

式中：Pi为有功功率；Qi为无功功率。

(2)变量约束

控制变量：

(5)

式中：VG为发电机的端电压；T为可调变压器的变比；QC为补偿电容发出功率。

状态变量：

(6)

式中：VL为负荷节点电压；QG为发电机无功出力。

1.3　归一化处理

由于各目标函数量纲不同，不能进行统一加权，故作如下归一化处理：

(7)

式中：Ploss0,dv0分别为初始有功网损和电压偏移；Plossmin,dvmin分别为进行单目标优化时得到的最优值；VSM本身无量纲，为使所求各目标函数有统一的最小值形式，故取倒数[5]。归一化得到的总的目标函数如下：

(8)

w1,w2,w3分别为各目标函数的权值，且w1+w2+w3=1。

2粒子群算法和单纯形法

2.1　标准粒子群算法

粒子群优化算法(PSO)是由Kennedy 和Eberhart根据鸟群觅食行为于1995年提出的一种群智能优化算法[6]，参数较少，操作简单。PSO算法中每个粒子根据自己和同伴的飞行经验来对速度和位置进行更新。公式如下：

(9)

(10)

式中：vij(k)，xij(k)分别为粒子i在第k次迭代中速度和位置的第j维分量；ω为惯性权重；c1、c2为学习因子；pij(k)为粒子i个体极值点位置的第j维分量；pgj(k)为粒子群体全局极值点位置的第j维分量；r1、r2为[0,1]之间的随机数。

2.2　骨干粒子群算法

F.van den Bergh等人证明了在迭代次数趋向于无穷时，标准粒子群优化算法中的目标函数不是以概率1完全收敛于最优解[7]，Clerc和Kennedy通过分析粒子的飞行轨迹，得出粒子都向它的个体最优位置和全局最优位置的加权平均值收敛[8]即：

(11)

当迭代次数达到无穷大时，所有的粒子都将最终收敛到同一个点。根据这种理论，Kennedy于2003年提出了骨干粒子群算法(B BPSO)[6]。BBPSO是利用以(pij(k)+pgj(k))/2为均值，以|pij(k)-pgj(k)|为标准差的高斯分布对粒子位置进行更新：

(12)

N(.)是高斯分布。随后，Kennedy又提出了骨干粒子群的另一种形式，采用下式对粒子位置进行更新：

(13)

大量的研究证实，骨干粒子群算法具备强大的全局搜索能力，而且不需设置各控制参数，算法更加优良。

2.3　单纯形法

单纯形法由Nelder与Mead提出的一种直接搜索方法，具备极强的局部搜索能力。其主要核心思想是：在一个n维空间中，构造出一个具有n+1个顶点的几何体，分别求出各个顶点的目标函数值，确定出目标函数值最大，次最大，最小的顶点，求出除目标函数值最大顶点外其余n个顶点的形心，在每一次迭代中，通过反射、收缩、扩张等策略找出一个较好点来取代最大点，从而形成一个新的几何体，通过这样不断地反复迭代，最终会找到或逼近一个局部最小解。

具体求解步骤如下：

(1)确定起始点。

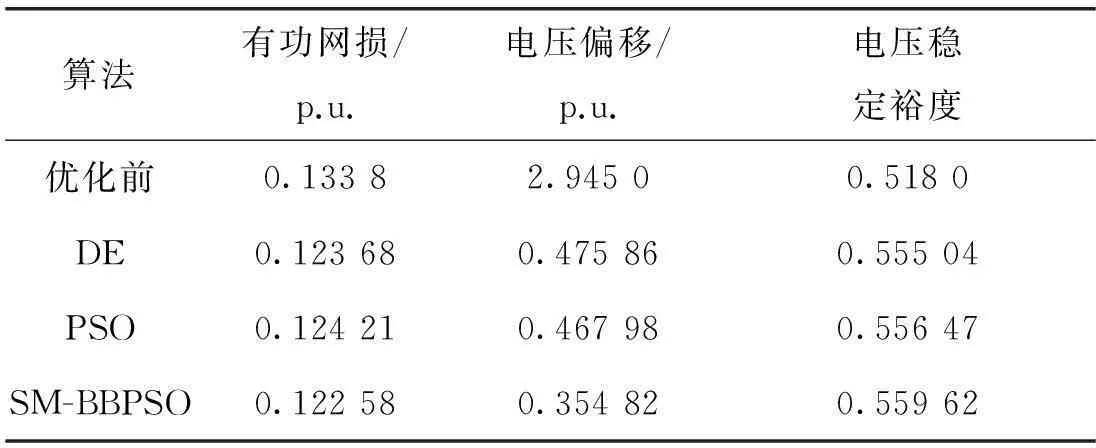
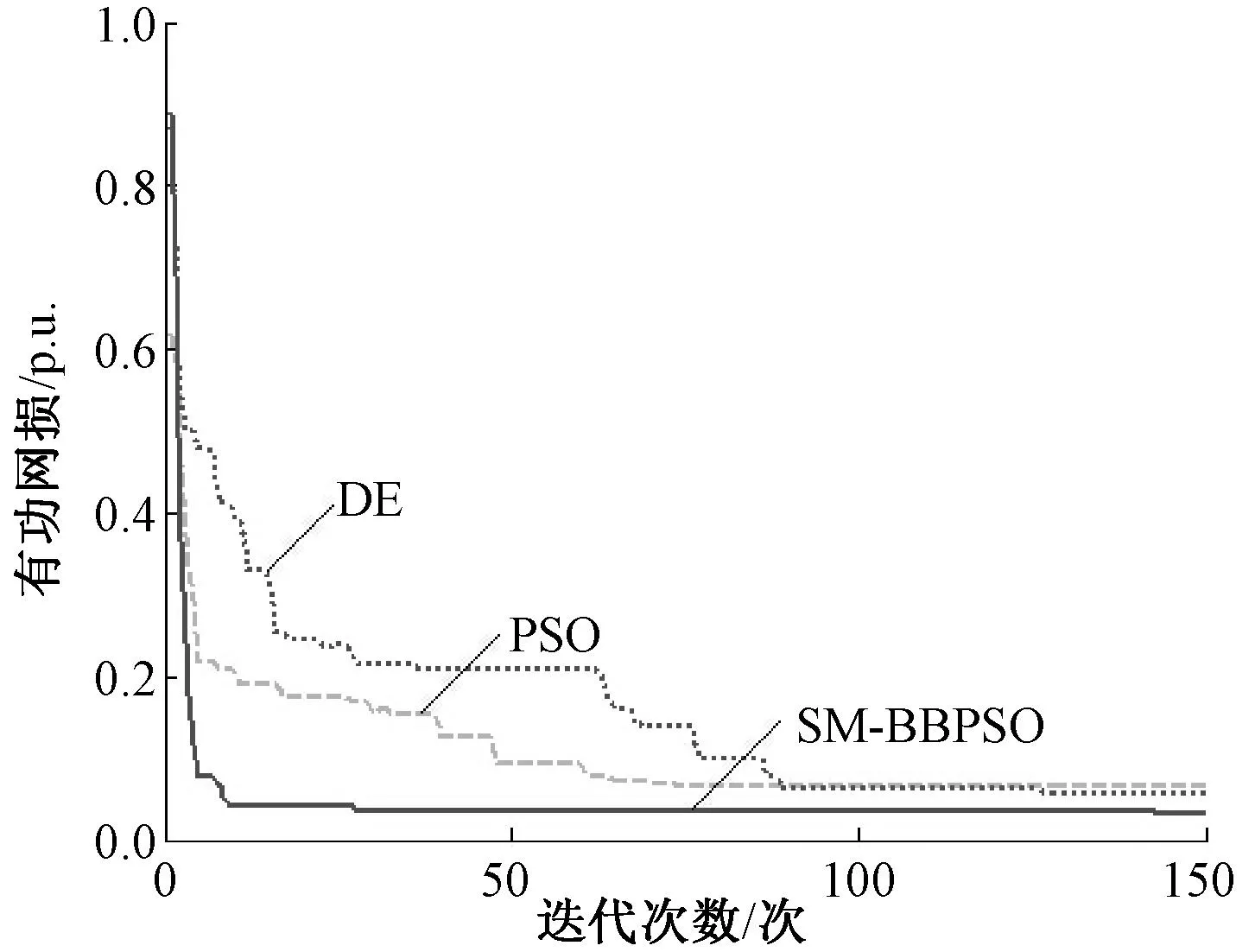
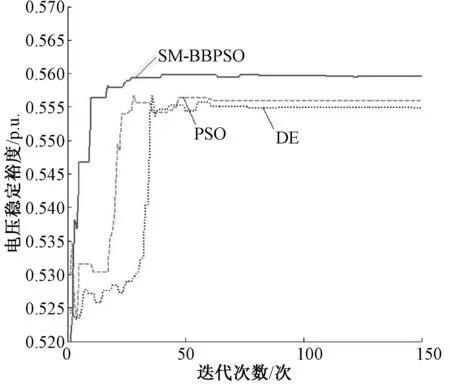
(2)反复操作:求出n+1个顶点的函数值, 确定其中的函数最大值fG、次大值fH和最小值fL, 除去函数值最大的点X(G)，并求出其他n个点的形心X,然后计算得出X(G)关于形心X的对称点X(n+2),计算X(n+2)的函数值。若f(X(n+2))1, 其初始值可取2, 并计算X(n+3)的函数值。若f(X(n+3))

(3)若fL≤f(X(n+2)) ≤fH,则用X(n+2)取代X(G)并转步骤(5)。

(4)若f(X(n+2))≥fH,则说明需要内缩。f(X*)=min{f(X(n+2)),f(X(H))},X(n+4)=X+β(X*-X), 其中β=0. 5,计算f(X(n+4))。若f(X(n+4))≤f(X*), 则用X(n+4)取代X(G)并转步骤(5);若f(X(n+4))>f(X*),则进行缩边,X(i)=(X(i)+X(L))/2,i=1, 2, …,n+1,并转步骤(5)。

3混合骨干粒子群算法

尽管骨干粒子群算法有较强的全局搜索能力，然而也有收敛速度慢的不足，故引入单纯形法，提高粒子的收敛速度。近年来，已有很多学者通过不同方式，把标准粒子群算法与单纯形法结合来提高粒子群算法性能。文献[9]、[10]分别是每一代和隔固定迭代次数对全局极值点进行单纯形搜索，虽然这样可以对粒子的质量有一定的提高，但是忽略了其他粒子得到的信息和经验。文献[11]是对每一个粒子进行单纯形搜索，虽然利用了粒子之间的信息和经验，但算法运算量较大，收敛时间上产生了代价。

本文运用K-均值聚类的方式来引入单纯形，形成一种混合骨干粒子群算法(SM-BBPSO)。首先利用骨干粒子群算法对粒子位置更新，然后运用K-均值聚类的方式，隔一定迭代次数对粒子进行分类，对每一类中的中心粒子进行单纯形搜索，使算法能够充分利用各粒子的信息和经验，增加种群多样性，又能减少粒子收敛时间，提高算法性能。

无功优化步骤：

Step1：导入算法的基本参数包括种群规模，粒子分类数k，单纯形搜索固定迭代次数K，以及对应电力系统中的潮流数据。

Step2：对粒子群体进行初始化，包括粒子的位置，速度，个体、全局极值，。

Step3：计算各粒子的适应度值并更新个体、全局极值。

Step4：判断t/K=[t/K](取整)是否成立，若成立，跳向Step5,否则跳向Step6。

Step5：通过K-均值聚类的方法对粒子群进行分类，计算得出每类粒子群的中心粒子，对中心粒子实行单纯形搜索，根据搜索结果，更新个体极值和全局极值。

Step6：按式(12)对粒子位置进行更新。

Step7：判断是否符合终止条件，若符合则停止运行，否则跳向Step3继续运行。

4算例及结果分析

为了验证算法的有效性、优越性，对IEEE-14节点系统，进行优化测试，并与其他优化算法比较。

4.1　测试数据

IEEE-14节点系统共有20条支路，5台发电机，3台有载调压变压器,1个并联补偿电容器节点。具体变量设置如下：

1,2,3,6,8节点为发电机，取节点1为平衡节点，节点2,3,6,8为PV节点；节点9为并联电容器安装节点；除1,2,3,6,8节点外，其他节点均为PQ节点。支路5-6，4-7,4-9为变压器支路。发电机端电压变化区间为[0.95,1.10](标幺值，系统基准容量为100 MVA，下同)；变压器变比调节区间为[0.90,1.10]，调节步长为0.012 5，即17档；电容器可调节区间为[0.00,0.50]；分类数k为2，间隔代数K为3，单纯形法代数为50。该系统初始有功网损、电压偏移、电压稳定裕度分别为0.133 8、2.945 0、0.518 0[12]。

4.2　优化结果分析

优化仿真结果如下所示。表1、表2为本算法与其他算法得出的数据比较。表1中有功网损、电压偏移数值由图1、图2中最终收敛值反代入式(7)所得。由表1可知三目标优化后都比优化前有了显著的提高，SM-BBPSO算法在有功网损上比DE、PSO算法分别减少0.89 %，1.3 %，比优化前减少8.4 %；电压偏移，电压稳定裕度也明显优于另外两种算法，可见本算法的优越性所在。

表1　IEEE-14节点系统各算法比较

表2　不同算法优化后控制变量的值

由图1可知，SM-BBPSO算法在优化有功网损过程中，在迭代次数接近30时就逐渐趋向于平稳，收敛速度明显快于DE、PSO算法，且有功网损数值明显小于另外两种算法，而有功损耗越小，则表明经济性越好。

图1　IEEE-14节点系统有功网损

由图2有，SM-BBPSO算法在优化电压偏移过程中，在迭代次数超过50时，才稳定，虽稍慢于PSO算法几代，但在迭代次数达到10时，该算法收敛曲线仍然下降很快，且收敛值也明显小于DE、PSO算法。可见该算法的优势还是可观的。而电压偏移越小，则表明电网的稳定性越高。

图2　IEEE-14节点系统电压偏差

由图3可知，SM-BBPSO算法在优化电压稳定裕度过程中，在迭代次数达到40时，就逐渐趋于稳定，在收敛速度上显然快于DE、PSO算法，且该算法电压稳定裕度较大，而裕度越大，则更有利于电网的安全性。

图3　IEEE-14节点系统电压稳定裕度

各算法优化后的节点电压的分布图如图4所示。

图4　优化后各节点电压分布

由图4可看出，为了保证电源设备的安全运行，在迭代过程中，PV节点转化为了PQ节点。SM-BBPSO算法优化后各节点电压值更接近期望值Vi*，波动较小，使得系统总体的节点电压偏移较小，明显优于DE、PSO算法。

综合以上可知，SM-BBPSO算法在同时对三个目标进行无功优化过程中，比起其他算法，不仅提高了解的质量和精度，也加快了收敛的速度，故可以更好地解决无功优化问题。

5结论

本文考虑有功网损、电压偏移最小及电压稳定裕度最大为目标，首次引入混合骨干粒子群算法用于解决电力系统无功优化问题。该算法利用骨干粒子群算法强大的全局搜索能力，提高了粒子质量，并借助K-均值聚类的方式引入单纯形搜索，提高了收敛速度和精度。将该算法应用于IEEE-14节点系统中，通过比较，结果表明了该算法的优越性和实用性，为求解无功优化问题，提供了一个新的方法。

参考文献:

[1]包黎昕，张步涵，段献忠,等. 电压稳定裕度指标分析方法综述[J]. 电力系统自动化,1999,23(8)：52-55.

[2]盛四清，李婧，田文树. 群智能算法在电力系统无功优化中的应用[J]. 电力科学与工程，2008,24(1)：1-4.

[3]马立新，单冠华，屈娜娜. 基于改进粒子群算法的电力系统无功优化[J]. 控制工程，2012，(19)：14-18.

[4]王攀攀，史丽萍，张勇，等. 采用一种混合骨干微粒群优化算法的感应电机转子断条故障诊断[J]. 中国电机工程学报，2012，32(30)：73-81.

[5]李莹，简献忠. 基于免疫进化细菌觅食算法的多目标无功优化[J]. 电力科学与工程，2014,30(4)：5-10.

[6]史丽萍，王攀攀，胡泳军，等. 基于骨干微粒群算法和支持向量机的电机转子断条故障诊断[J]. 电工技术学报, 2014, 29(1)：147-155.

[7]Frans V D B.An analysis of particle swarm optimizers[D]. Particle Swarm Optimization, 2002.

[8]Clerc M，Kennedy J.The particle swarm-explosion，stability，and convergence in a multidimensional complex space[J].IEEE Transactions on Evolutionary Computation, 2002, 6(1)：58-73.

[9]安伟刚，李为吉.改进的粒子群优化算法及其工程应用[J].机械科学与技术，2005，24(4)：415-417.

[10]Hsu C C，Gao C H. Particle swarm optimization incorporating simplex search and center particle for global optimization[C].Japan：IEEE，2008：26-31.

[11]王芳，邱玉辉.一种引入单纯形算子的新颖粒子群算法[J].信息与控制，2006，34(5)：517-522.

[12]冯士刚，艾芊. 带精英策略的快速非支配排序遗传算法在多目标无功优化中的应用[J]. 电工技术学报，2008，22(12)：146-151.

Three-objective Hybrid Bare-bones Particle Swarm Optimization for Reactive Power Optimization

Ma Lixin, Wang Jiyin, Xiang Qing，Huang Yanglong(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)