斜裂纹转子刚度特性分析

李志农, 夏恒恒, 肖尧先

(南昌航空大学 航空制造工程学院， 江西 南昌 330063)



斜裂纹转子刚度特性分析

李志农, 夏恒恒, 肖尧先

(南昌航空大学 航空制造工程学院， 江西 南昌 330063)

摘要：在材料力学和断裂力学的基础上，运用应变能释放率的方法，得出斜裂纹的刚度矩阵.讨论在裂纹全开的状态时，裂纹倾角、轴细长比和裂纹深度对转轴刚度的影响，并对裂纹处于旋转时的开闭情况及相应轴的刚度变化规律进行研究.结果表明：当裂纹处于全开状态时，随着裂纹倾角的增大，裂纹的刚度随之减小，轴刚度的变化随着裂纹深度的增大更加显著；当裂纹处于开闭状态时，随着裂纹深度的增加，轴的刚度不再一直减小，而是有一定规律的波动，即时变特性，此时，轴的耦合振动随之增强，转子的动力特性变得愈加复杂.

关键词：斜裂纹； 转子刚度； 时变特性; 开裂纹; 呼吸裂纹

疲劳裂纹是旋转类机械转轴上常见的故障之一，也是引起机械系统失效的主要原因.而含裂纹轴的非线性动力学特性主要是受转轴刚度的影响.因此，如何合理地建立含裂纹的转子系统动力学模型，计算裂纹转轴的刚度显得尤为重要.当前，国内外许多学者对裂纹的刚度模型进行了研究，并取得了一些成果[1-10].然而，裂纹全开和裂纹处于开闭交替时，裂纹转轴的刚度变化规律有显著的差别.基于此，本文通过应变能释放率的方法，得到斜裂纹轴的刚度矩阵，并使用应力强度因子为零法，近似模拟了裂纹的呼吸特点，着重分析裂纹倾角为45°时，在裂纹处于全开状态下，转轴轴细长比和裂纹深度比对转轴刚度的影响，以及裂纹处于开闭交替状态下，转轴的刚度变化规律.

1裂纹模型

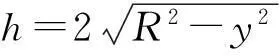
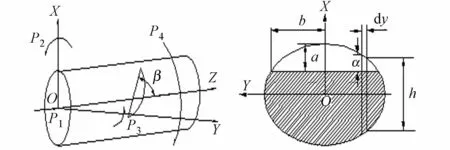
(a) 转轴的受力图 (b) 裂纹的截面图1　斜裂纹转轴Fig.1　Slant crack shaft

通过能量释放率的方法，求出裂纹的应变能，运用卡式定理求出裂纹轴的附加柔度.根据文献[6]提出的局部柔度理论，得出斜裂纹在P1～P4方向上的应力强度因子分别为

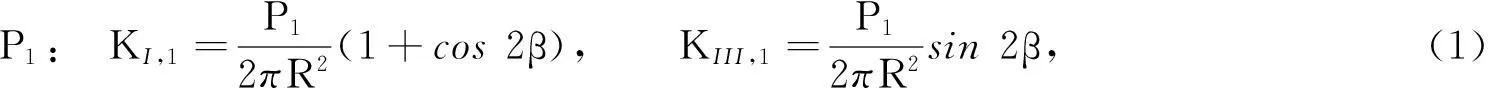
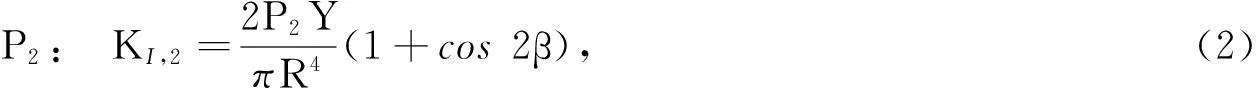
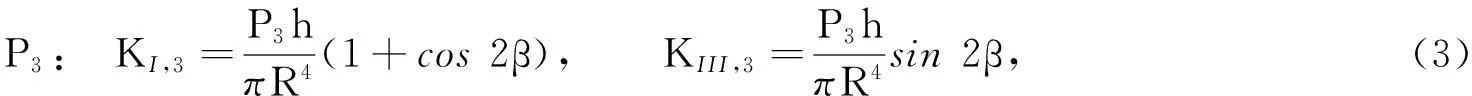
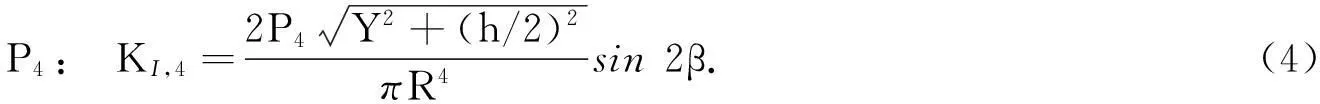
总的应力强度因子为

3个影响系数[6]分别为

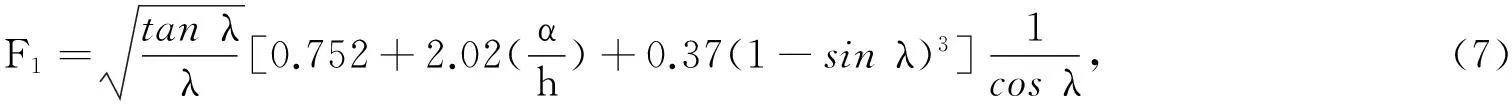
能量释放率密度函数可表示为

对式(10)进行积分，可得到裂纹轴释放的应变能为

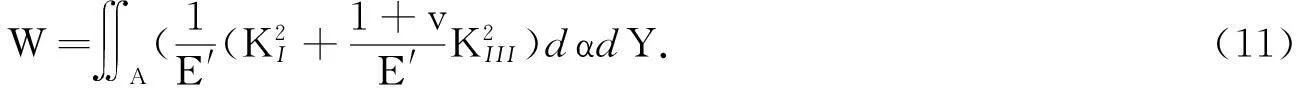
式(11)中：A为裂纹张开区域.因此，通过卡氏定理对其微分，得到裂纹轴的附加柔度为

无裂纹转轴的柔度矩阵[7]为

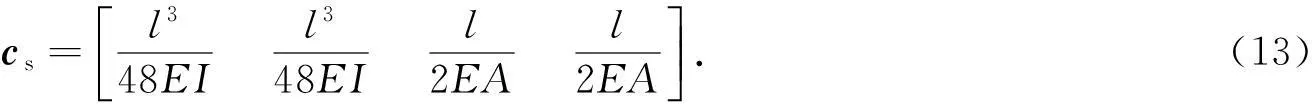
式(13)中:I=πd4/64.由裂纹轴的附加柔度加上无裂纹轴的柔度，可得裂纹轴的柔度为

其中,

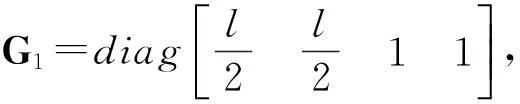
(15)

故裂纹轴的刚度可表示为

为了更加直观地表示出裂纹对刚度的影响，采用裂纹的无量纲刚度表示，即

2斜裂纹全开时转轴刚度特性分析

不同裂纹倾角下，裂纹的无量纲刚度的变化情况，如图2所示.图2中：α/R为裂纹深度比.由图2可知：裂纹轴的刚度随着裂纹深度比的增加而减小；当裂纹深度相同时，裂纹轴的刚度随着裂纹倾角的增大越来越小，且减小的速率越大.

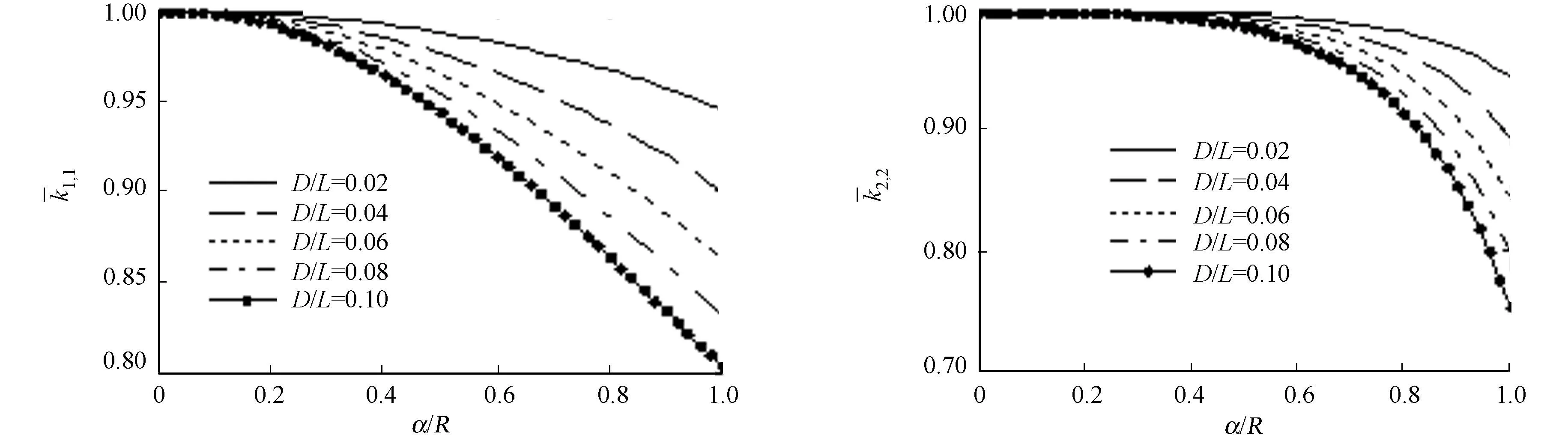
(a) 1，1 (b) 2，2

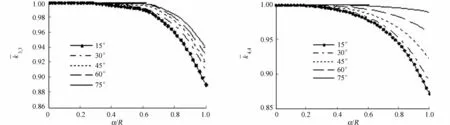
(c) 3，3 (d) 4，4图2　不同裂纹倾角对裂纹转轴的刚度变化对比图Fig.2　Stiffness of the cracked shaft with different crack inclination angle

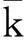
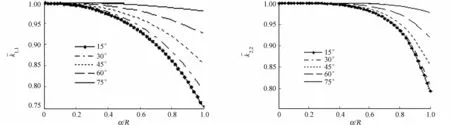
(a) 1，1 (b) 2，2

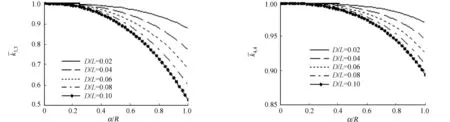
(c) 3，3 (d) 4，4

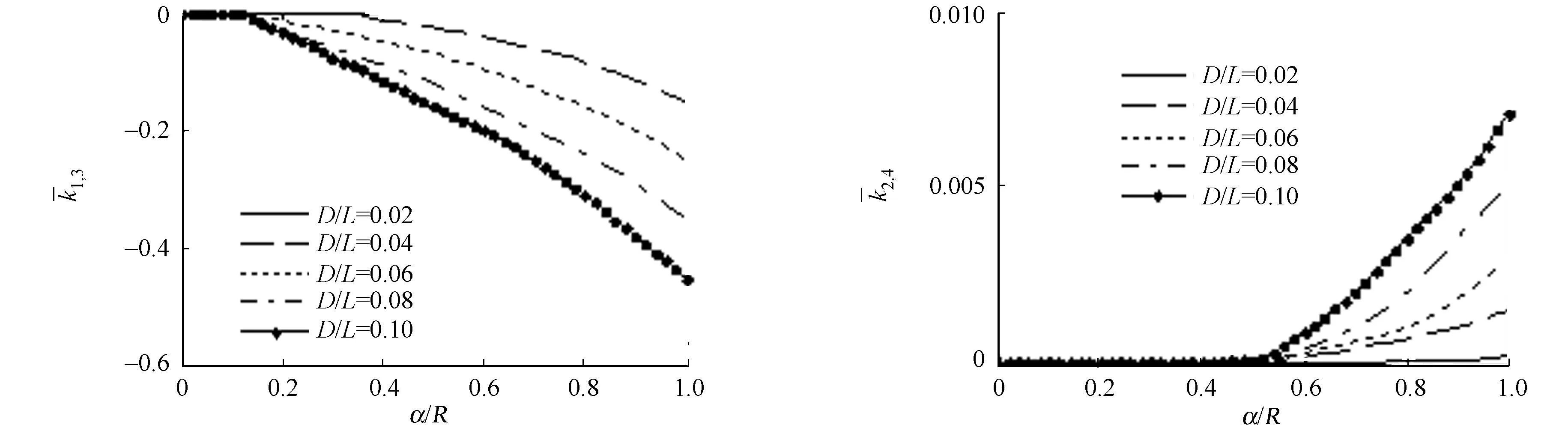
(e) 1，3 (f) 2，4图3　转轴细长比对裂纹轴刚度的变化图Fig.3　Stiffness of the cracked shaft with the axial slenderness ratio

3斜裂纹截面开闭特性

裂纹开闭线位置(CCLP)变化点分布,如图4所示.将裂纹边界平均分成50等份，通过式(5)可计算出裂纹边缘线各点的总应力强度因子，确定KI的正负号的位置.通过该位置作垂直于裂纹边界的直线，该直线就是裂纹的开闭线.由图4可知：开闭线一侧区域的点由于受到拉应力而张开，而另外一侧区域的点由于受到压应力而闭合，这样可以得到转轴在不同转角下的裂纹开闭区域.在一个稳态的旋转周期内，可以得到裂纹的开闭特性即呼吸特性；当CCLP确定，可以确定裂纹转轴刚度求解的积分区域，从而求出该积分区域下的裂纹转轴刚度矩阵.

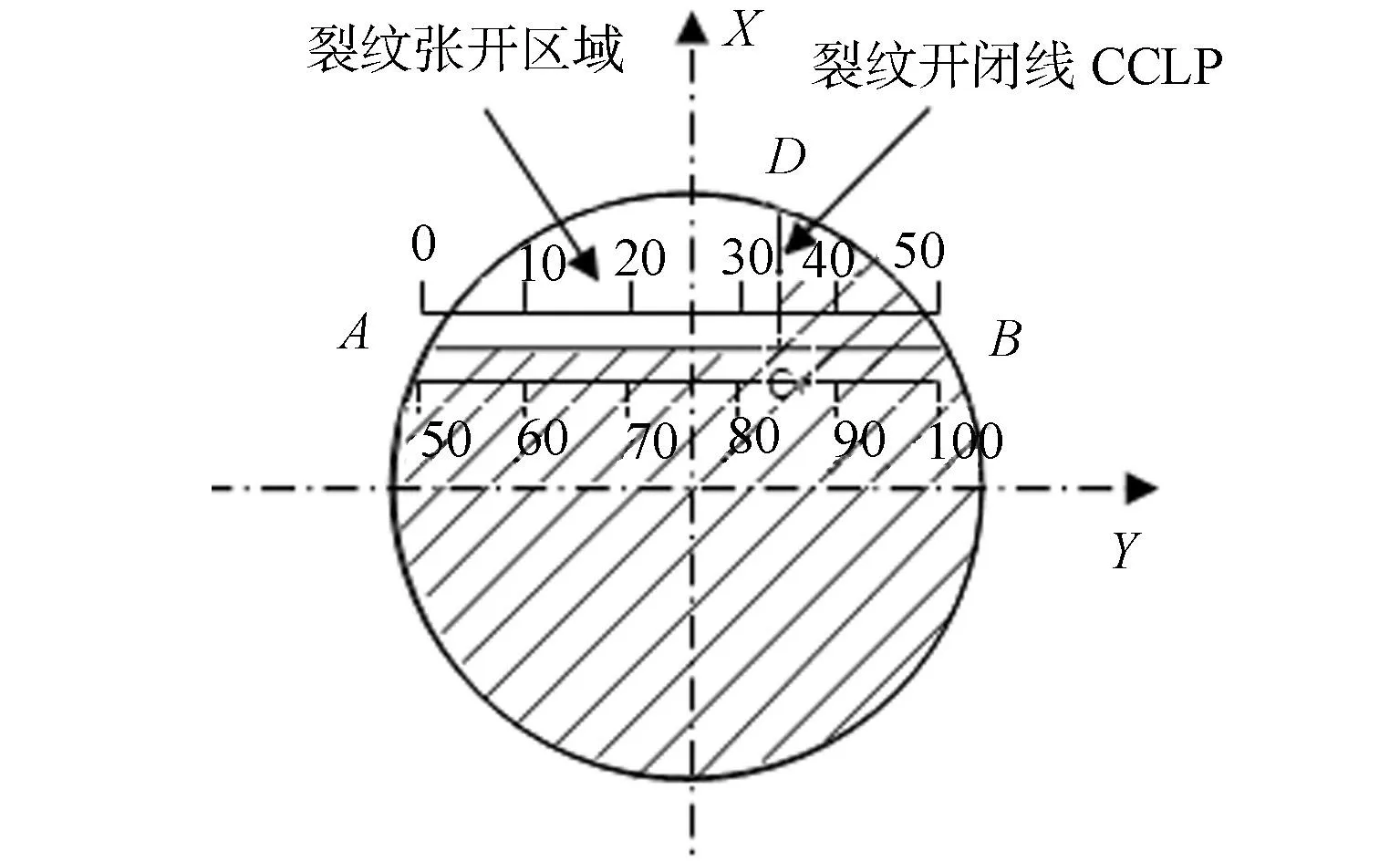
图4　裂纹开闭线位置变化点分布图Fig.4　Changing point distribution ofcrack opening and closing line position

运用牛顿第二定律，在Jeffcott转子模型的基础上，可以建立裂纹转子的动力学方程，即

裂纹轴长度为260mm，裂纹轴直径为9.5mm，转盘质量为0.6kg，转盘尺寸为Φ76mm×25mm，弹性模量E为210GPa，阻尼系数C为40kg·s-1，转盘的偏心量e为0.16mm，经计算求得无裂纹转子系统横向振动固有频率为3 928r·min-1，转子旋转速度为2 000r·min-1.以无裂纹转子的静态作为裂纹完全闭合的初始状态，可以求出裂纹轴刚度，运用龙格库塔法求得此时转子系统横向振动响应，从而得到作用在裂纹截面上的力.此时,利用应力强度因子为零法可确定CCLP，从而求出刚度矩阵.然后,通过刚度矩阵得出转子转过一定角度时的振动响应，如此循环，又可以确定CCLP，得到转子在一个稳态的旋转周期内的裂纹开闭规律.

当裂纹深度比为0.2时，一个稳定周期内裂纹开闭过程如下：转子旋转角度φ在0°～66°时，裂纹处于闭合阶段；当转角超过66°时，裂纹开始张开，到128°时，完全张开，一直持续到246°，再闭合，直到转过360°完成一个旋转周期；裂纹处于闭合与全开时的角度跨度都为181°.

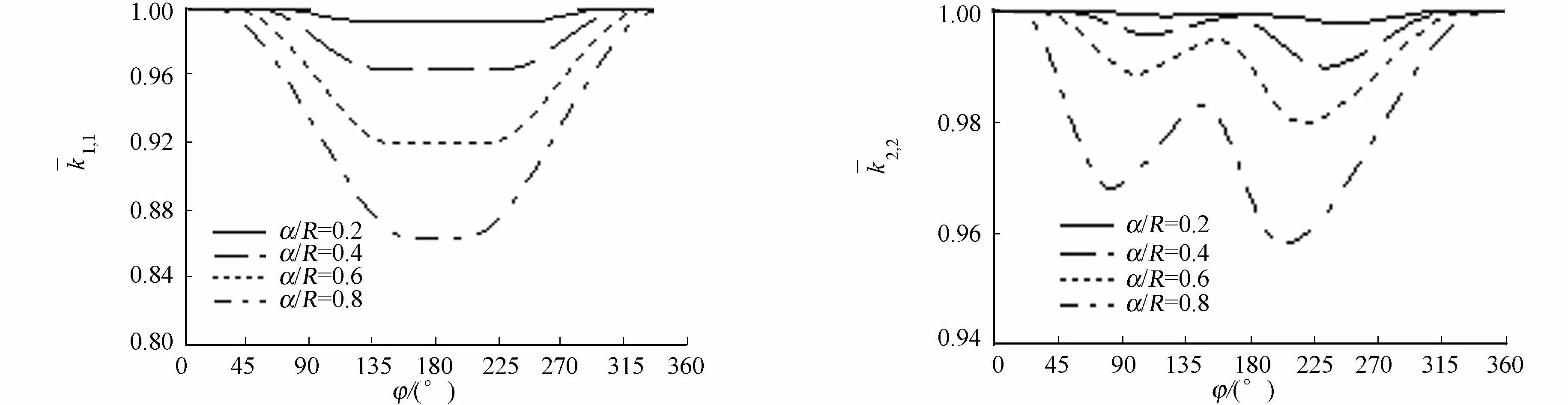
(a) 1，1 (b)2，2

(c) 3，3 (d) 4，4

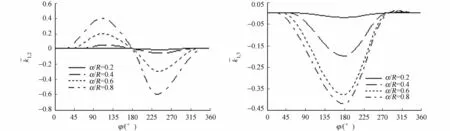
(e) 1，2 (f) 1，3

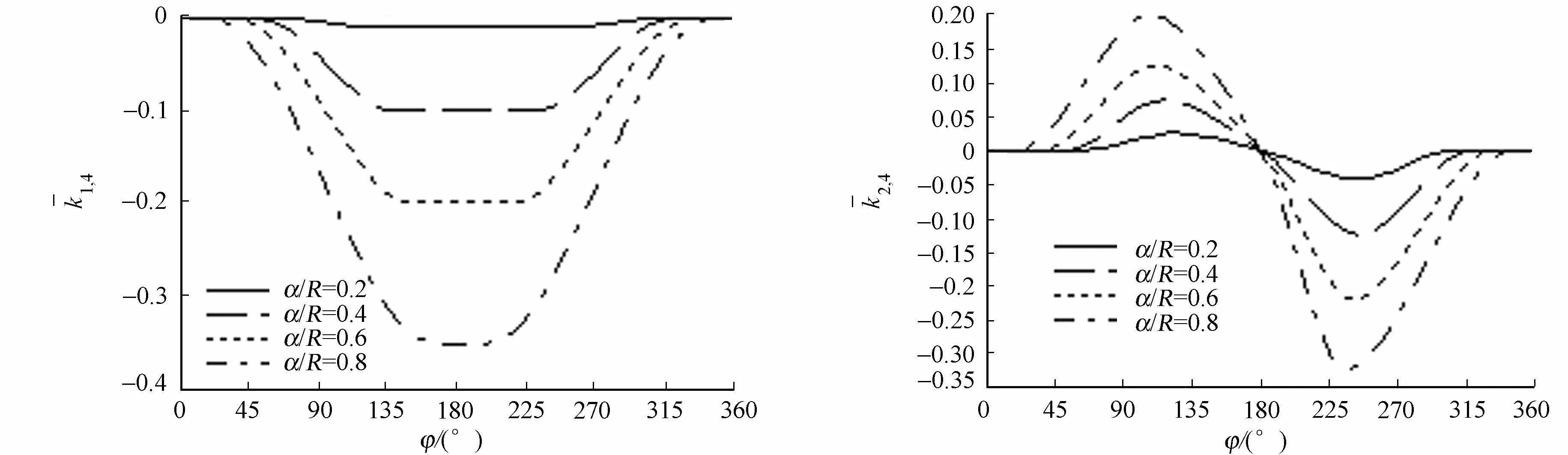
(g) 1，4 (h) 2，4图5　裂纹轴刚度随旋转角和裂纹深度的变化Fig.5　Variation of crack shaft stiffness with rotation angle and crack depth

4结论

从转轴裂纹全开状态和裂纹的时变特性两方面研究斜裂纹转子刚度特性，得出以下2点结论.

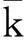
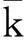
参考文献：

[1]GASCH R.A survey of the dynamic behavior of a simple rotating shaft with a transverse crack[J].J Sound and Vibration，1993,160(2):313-332.

[2]高建民,朱晓梅.转轴上裂纹开闭模型的研究[J].应用力学学报,1992,9(1):108-112.

[3]PAPADOPOULOS C A,DIMAROGONAS A D.Coupled longitudinal and bending vibrations of a rotating shaft with an open crack[J].Journal of Sound and Vibration,1987,117(1):81-93.

[4]曾复,吴昭同.含横向裂纹简单转子刚度的计算[J].机械科学与技术,1999,18(5):745-747.

[5]林言丽.斜裂纹转子动力学特性的研究[D].北京:清华大学,2008：20-25.

[6]DARPE A K.Dynamics of a Jeffcott rotor with slant crack[J].Journal of Sound and Vibration,2007,303(1):1-28.

[7]DARPE A K,GUPTA K,CHAWALA A.Coupled bending, longitudinal and torsional vibrations of a crack rotor[J].Journal of Sound and Vibration,2004,269(1/2):33-60.

[8]何为,任兴民,杨永锋.横向裂纹轴耦合刚度分析[J].振动与冲击,2007,26(12):44-48.

[9]SEKHAR A S.Crack identification in a rotor system: A model-based approach[J].Journal of Sound and Vibration,2004,270(4):887-902.

[10]王宗勇,林伟,闻邦椿,等.开闭裂纹转轴刚度的解析研究[J].振动与冲击,2010,29(9):69-72.

(责任编辑： 钱筠 英文审校： 杨建红)

Stiffness Characteristics Analysis of a Rotor With Slant Crack

LI Zhinong, XIA Hengheng, XIAO Yaoxian

(School of Aeronautical Manufacturing Engineering, Nanchang Hangkong University, Nanchang 330063, China)

Abstract：The stiffness matrix of the slant crack was obtained based on material mechanics and fracture mechanics theory through the use of strain energy release rate method. While the crack is fully open, the influence of the crack angle, the axial slenderness ratio and the crack depth on the stiffness of the shaft was discussed. At the same time, the opening and closing conditions in the rotating state and the stiffness change law of the corresponding shaft were studied. The results show that, when the crack is in the fully open state, the stiffness of the crack decreases with the increase of the crack angle. And the shaft stiffness changes more significantly with the increase of the crack depth; when the crack is in the opening and closing state, with the increase of the crack depth, the shaft stiffness is no longer decreases, but there is a certain law of fluctuation, which is time-varying characteristics, in this case, the shaft coupling vibration also increases, the dynamic characteristics of the rotor becomes increasingly complex.

Keywords：slant crack; rotor stiffness; time-variant characteristics； open crack； breaking crack

基金项目：国家自然科学基金资助项目(51265039， 51075372, 50775208); 江西省研究生创新专项资金资助项目(YC2014-S390); 江西省教育厅科技计划项目(GJJ12405); 重庆大学机械传动国家重点实验室开放基金(SKLMT-KFKT-201514)

通信作者：李志农(1966-)，男，教授，博士，主要从事智能检测方面的研究.E-mail:lizhinong@tsinghua.org.cn.

收稿日期：2015-07-10

中图分类号：TH 133

文献标志码：A

doi:10.11830/ISSN.1000-5013.2016.01.0001

文章编号：1000-5013(2016)01-0001-06