基于等残留高度的球形曲面的数控加工*
西庆坤
(四川工程职业技术学院 机电工程系,四川 德阳 618000)
基于等残留高度的球形曲面的数控加工*
西庆坤
(四川工程职业技术学院 机电工程系,四川 德阳618000)
摘要:在对球头铣刀精加工球形曲面的残留高度研究的基础上,同时分析了残留高度与表面粗糙度之间的关系,根据残留高度计算了球头铣刀步进角的大小。通过控制步进角完成曲面加工,达到有效控制球形曲面在手工编程中的残留高度,以满足零件表面粗糙度的要求。以半球曲面为例,基于等残留高度进行球形曲面精加工数控宏程序的设计,同时采用连续进给编程的方法,有效保证了零件的加工质量,提高了加工效率,为球面数控加工的设计提供了编程方法与策略。
关键词:等残留高度;表面粗糙度;连续进给;球形曲面;数控加工
0引言
球形曲面是最基本的曲面之一,如球面阀、滚珠和相应的球面槽等零件都有这样的轮廓。而球面的加工既要保证精度和表面粗糙度要求,又要经济合理,因此合理的确定走刀路线非常重要,而在实际的生产过程中,操作者常是根据经验或试加工来确定步长保证零件的加工精度。因此,合理的确定走刀步长是曲面加工中要解决的一个重要问题。很多学者在自由曲面的加工中对步长的控制提出各种算法,如参数线加工方法、截面线加工方法、导动面法等[1]。其中的一种算法为等残留高度[2-3],而在这些算法都是通过编程软件来生成刀具的路径,然后自动生成数控加工程序,对编程者的软件操作和数学知识要求较高。因此本文探索利用三坐标铣床加工球面,用手工编程来实现基于等残留高度的球面宏程序的编制方法。为有效的保证球形曲面类零件的加工质量和提高加工效率,具有重要的实际意义。
1球形曲面残留高度的计算
本文研究球头铣刀精加工球形曲面时残留高度的大小,如图1所示,球面半径为R,球头刀半径为r,当采用等角度加工时,刀具切削一圈,加工弧长递增圆心角为θ,则H即为残留高度值。
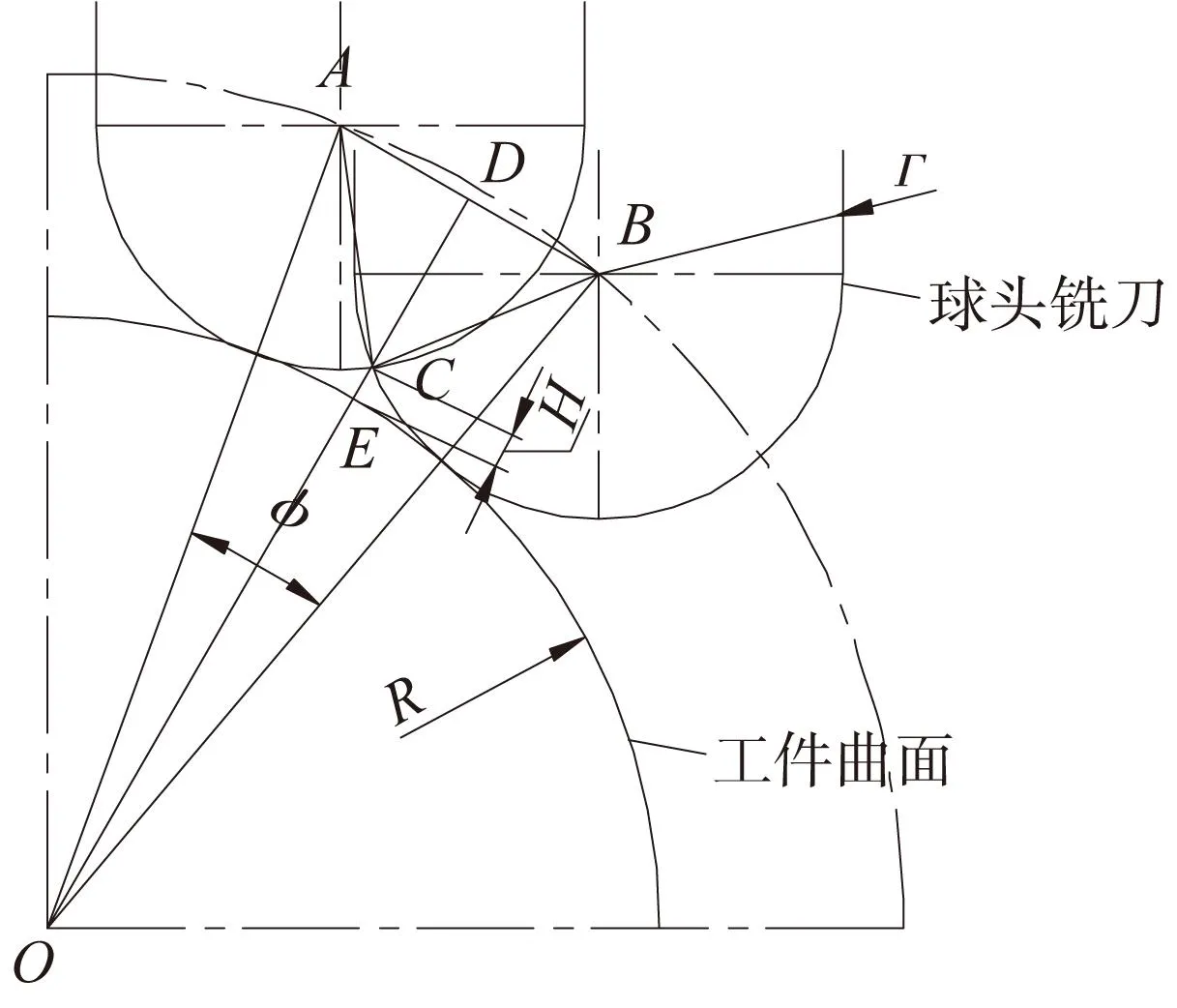
图1 球形曲面加工中残留高度计算示意图
由图1可知:残留高度H即为图中CE,
CE=DE-CD
而
(1)
在△ACD中
(2)
所以
(3)
由上式可知,当球形曲面半径R确定时,加工的残留高度由球头刀半径r和步进角θ决定。因此要合理的选择球头刀半径r和步进角θ的大小,保证零件加工残留高度在精度范围内。
另外残留高度受球头铣刀刀具行间相位差影响也较大[4],相位差由刀具的齿数和每齿进给量决定。而在刀具齿数选定的情况下,在如图1的球形曲面加工中,进给量的控制要求也是一个变化的值,给编程带来一定的难度。
那么在选定刀具的情况下,步进角的控制就直接影响零件加工的残留高度。所以,在残留高度确定的情况下,如何选择步进角的大小至关重要。
由式(3)可推导求得:
(4)
上式即为根据残留高度确定步进角的公式。
2表面粗糙度和残留高度的关系
影响表面粗糙度的因素可以分成为几何因素和非几何因素。几何因素主要包括:刀具半径R、刀具每转进给量、行间距S等。影响粗糙度的非几何因素包括:积屑瘤、鳞刺、振动、切削刃的刃磨质量、工件材料组织的缺陷、切削液的使用情况等。在精加工时,非几何因素影响较小,可忽略不计,而几何因素是影响精加工表面粗糙度的主要因素[5]。
残留高度是指刀具两行间的残留量。在几何因素中,铣削残留高度决定了铣削表面粗糙度的大小。在精加工时,因此一般通过控制铣削残留高度的大小来控制表面粗糙度,从而控制零件表面加工质量。
3加工示例
本示例以简单的半球曲面精加工为例,如图2所示。刀具采用φ8球头铣刀,用残留高度控制刀具的进给路径,以达到在满足加工精度的前提下减小走刀路线。

图2 半球曲面示例
3.1加工方法
用三坐标机床加工曲面属于近似加工,常用的加工方法有等高线编程方法,而等高线加工存在加工路线长,空行程多,在停刀处有驻刀痕等问题。现在比较高效、高精度的数控走刀方式应该是螺旋式走刀方式[6],进行连续进给切削,同时控制三个坐标轴的运动,走刀和下刀同时进行,改变以往等高线加工下刀和走刀分开的现象,此时就不存在每一次走刀都需要切入和切出,浪费走刀路线的问题。
本文探索采用连续进给加工。一种方法是数控系统具有的变径螺旋插补功能,另一种方法是采用极坐标连续进给的编程方法,本文对比两种方法,“自上而下”对半球进行连续加工。
3.2编程思路
根据零件表面粗糙度Ra要求获得残留高度H值,然后计算刀具每绕着球面转一圈进给的角度θ,即步进角θ,使刀具沿着球面进行螺旋插补。
3.3加工程序
方法一:采用极坐标连续进给的编程方法。将球心作为零件加工原点基于FANUC-0i数控系统进行程序编制[7-8],程序中各变量含义如表1所示。

表1 宏程序中各变量的定义
主程序
O0922/加工主程序
G54 G90 G00 X0 Y0/建立工件坐标系,绝对坐标编程,快速定位到X0Y0
M03 S1600/启动主轴
G65 P1922 A50 B4 C90 E0.0063 I0 S1/调用宏程序,并给变量赋值
M30 /程序结束
宏程序
O1922/宏程序名
N1#12=#1+#2 /球心与刀心连线距离(常量)
N2#16=#1*#1+#1*#2+#1*#8+0.5*#8*#8/计算中间变量#16
N3#17=#1*#1+#1*#8+#1*#2+#8*#2/计算中间变量#17
N4#18=#16/#17/计算中间变量#18
N5#19=2*ACOS[#18] /计算步进角#19
N6G00X20Y0/X、Y方向定位
N7Z[#12+10]/下刀
N8G01Z#12F300/Z方向下刀
N9#7=#12*COS[#3]/ 任意角度时铣刀球心的X坐标值
N10G01X#7F300/切入
N11WHILE[#3GT#4]DO1/如果#3<#4,循环1继续
N12#3=#3-#19/360/角度每次递减#19/360
N13#7=#12*COS[#3]/ 任意角度时铣刀球心的X坐标值
N14#8=#12*SIN[#3]/ 任意角度时铣刀球心的Z坐标值
N15#11=#11+#19/极角#11每次递增#19
N16#11=#11-ROUND[#11/360]*360/当角度大于360度时取余
N17G16/极坐标编程
N18G02 X#7 Y#11 R#7 Z#8 F100/三坐标联动,极半径#7,极角#11,每次插补的Z坐标为#8
N19G15/极坐标编程取消
N20END1/循环1结束
N21G01Y100F300/切出
N22G01X100
N23G00Z[#12+100] /抬刀至安全高度
N24M99 /宏程序结束返回如下
3.4刀具路径轨迹
采用数控仿真软模拟刀具路径轨迹及加工出的零件如下(为了刀路显示清楚,增大了步进角的刀路),说明编制的宏程序正确,可以实现循环,刀具路径轨迹如图3所示。

图3 极坐标连续进给数控仿真路径轨迹图
方法二:采用数控系统具有变螺距螺旋插补功能,但在一个螺距内的半径必须保持不变,这样在改变半径时就会出现折线,即:
如果将N11到N20间程序段改为[7]:
N11WHILE[#3GT#4]DO1
N12#7=#12*COS[#3]
N13#3=#3-#19
N14#6=#12*SIN[#3]
N15#8=#12*COS[#3]
N16G02X#8I-#7Z#6F100
N17END1
刀具路径轨迹如图4所示。

图4 变螺距螺旋插补数控仿真路径轨迹图
3.5结果分析
本文探讨的连续进给编程路径连贯,不会出现陡然的转折,可有效保证零件的加工质量。并根据零件表面粗糙度要求计算步进角的大小,在满足零件的表面粗糙度要求的前提下刀路最短。
4结论
本文推导出球形曲面的残留高度公式,加工的残留高度受球头刀半径和每齿进给量和步进角影响。在刀具选定的条件下,选择合适步进角,节省走刀路线,减小数控系统的计算量,又能保证零件的加工质量在精度要求范围内,提高零件的加工效率具有重要的现实意义。为三坐标机床加工球形曲面的数控宏程序的设计提供编程方法和策略。
对于曲率半径变化不大的曲面,可近似利用球形曲面的残留高度计算方法,在编制数控加工程序时,可采用用圆弧段逼近曲面形状,采用极坐标编程方法。因此该方法具有很好的推广价值。
[参考文献]
[1] 乐英,韩庆瑶,贾军.复杂曲面数控加工刀具轨迹的生成技术[J].机床与液压,2008,36(6):25-26.
[2] 陈晓兵,廖文和,吴海兵.三角网格表面等残留高度刀轨生成算法[J].计算机辅助设计与图形学学报,2009,21(12):1803-1804.
[3] 孟献军.五轴数控加工刀位算法研究[J].制造技术与机床,2009(1):26-28.
[4] 吕彦明.球头刀高速铣削残留高度研究[J].模具技术,2002(6):14-16.
[5] 王明海,孙越.整体叶盘叶片铣削加工表面质量控制仿真研究[J].机械设计与制造,2013(4):177.
[6] 李海滨,唐小波,高天宇.叶片数控加工表面粗糙度控制的研究[J].机床与液压,2011,39(23):14-16.
[7] 陈海舟.数控铣削加工宏程序及应用实例[M].北京:机械工业出版社,2005.
[8]彼得.斯密德.数控编程手册[M].罗学科,译.北京:化学工业出版社,2005.
(编辑赵蓉)
The NC Machining of Spherical Surface Based on Constant Scallop-height
XI Qing-kun
(Department of Mechanical Engineering, Sichuan Engineering Technical College, Deyang Sichuan 618000,China)
Abstract:On the basis of studying on the residual height of spherical surface for finishing by ball end milling cutter, and analyzing the relationship of residual height and surface roughness, ball milling step angle was calculated based on residual height. Surface machining was completed by controlling step-angle. The residual height of spherical surface was controlled effectively during manual programming. The requirements of surface roughness was satisfied. NC macro program of spherical surface finishing was designed based on constant scallop-height, for example hemispherical surface. At the same time, Using the method of continuous feed programming, processing quality was ensured and processing efficiency was improved. The programming method and strategy were provided for the design of spherical surface NC machining.
Key words:constant scallop-height; surface roughness; continuous feed; spherical surface; NC machining
中图分类号:TH165;TG547
文献标识码:A
作者简介:西庆坤(1981—),女,吉林梅河口人,四川工程职业技术学院讲师,硕士,加工中心技师,研究方向为数控技术研究,(E-mail)xiqingkuni@126.com。
基金项目:德阳市科技支撑项目:基于残留高度控制的二次曲面铣削方法研究(DYCC20150134)
收稿日期:2015-03-12;修回日期:2015-04-06
文章编号:1001-2265(2015)12-0130-03
DOI:10.13462/j.cnki.mmtamt.2015.12.035

